考虑风浪相关性的列车-桥梁耦合振动分析

2022-08-12崔圣爱曾慧姣

东南大学学报（自然科学版） 2022年4期

崔圣爱郭晨张猛曾慧姣刘品祝兵

(1西南交通大学土木工程学院, 成都 610031)(2成都大学建筑与土木工程学院, 成都 610106)

随着铁路网从内陆向沿海延伸,近海区域出现越来越多的高速铁路跨海桥梁,如平潭海峡公铁两用桥、港珠澳大桥等.不同于内陆区域,跨海高速铁路桥梁所处的海洋环境极为复杂,常会遭受不同程度的台风、巨浪等复杂海洋动力环境的侵袭.平潭海峡气象监测数据表明,沿线6级及以上大风每年发生天数超过300 d,8级及以上大风发生天数达90 d，年平均波高为1.1 m,平均周期为5.4 s.

学者们对于风荷载作用下的列车桥梁动力响应进行了大量研究.Liu等[1-2]结合流体动力学、有限元方法及多体动力学,研究了列车交汇下的车桥动力响应及表面压力特性.Olmos等[3]建立了风-车-桥耦合振动模型,研究了横风作用下高墩高架桥上列车的运行安全性,并确定临界风速为25 m/s.基于风洞试验,Xue等[4]研究了挡风墙高度及透风率等因素对车-桥耦合振动特性的影响,发现桥面板上的风障对桥梁侧向力系数和风-车-桥系统的动力响应都存在显著影响.曹艺缤[5]建立了不同风速及多个波浪重现期的组合模型,发现随着风速及波高的增大,车桥系统响应基本呈上升趋势.房忱等[6]基于车-桥耦合动力仿真方法,讨论了不同波浪重现期、车速、水深和桥墩刚度等因素对车-桥系统的影响.然而，已有研究中通常假设风场和波浪场相互独立,忽略了风、浪荷载之间的相关性.Copula分布能准确地描述多维变量间的相关性,目前已被广泛用于金融、岩土及水文等领域,但在桥梁工程领域应用较少.

本文基于Copula分布建立了风速波高的联合分布,得到不同重现期下风浪要素.选取某一大跨斜拉桥为研究对象,基于考虑轮轨接触关系非线性、蠕滑力-蠕滑率非线性关系及悬挂参数非线性,建立了综合考虑风浪车桥相互作用的有限元与多体动力学模型,对单风、单浪及风浪联合作用下的车桥响应进行深入分析,研究风速、波高对车桥响应的影响.该方法可为后续跨海大桥的列车行车安全性及舒适性评估提供参考.

1 风浪要素分布模型

风浪联合作用是常见的气象现象,但其相互作用机理复杂,两者相生相伴并且相互影响.研究车桥系统在风浪联合作用下的动力响应时,风浪场要素的同步测量非常重要.

1.1 边缘分布模型

根据平潭海洋站观测得到的台风期实测数据,分别对风速和波高进行多种分布拟合,建立风浪要素的边缘分布.图1给出了双要素的频率直方图、对数正态(lognormal) 分布、威布尔(Weibull) 分布、耿贝尔(Gumbel) 分布及广义极值(GEV)分布的概率密度曲线.由图可知,风速Uw和波高Hs的广义极值分布、威布尔分布与各自的频率直方图更为贴合.基于极大似然估计得到各边缘分布的参数值,计算出风速、波高在不同分布函数下的均方根误差(RMSE).RMSE越小表明该分布对原始数据的拟合效果越好(见表1).

(a) 风速概率统计

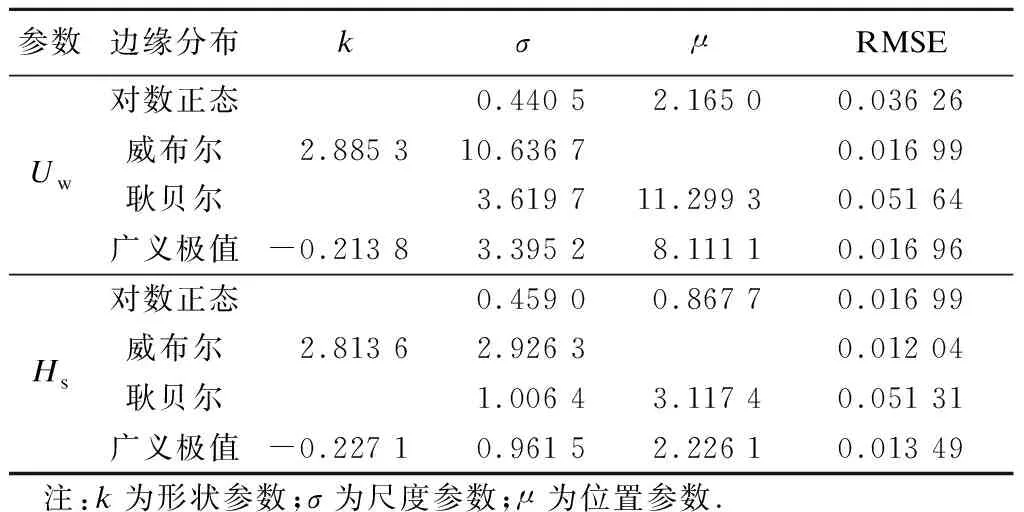
表1 边缘分布参数及RMSE值

1.2 Copula分布模型

Genest等[7]给出了Copula分布的定义.对于二维变量,Copula分布表达式为

(1)

确定Copula分布即是计算相关参数θ的过程.在Copula分布中,相关参数θ是表征变量间相关性的重要指标.常用的度量指标包括Pearson线性相关系数ρp和Kendall秩相关系数τ.ρp只能描述变量间的线性相关性,具有较大的局限性.而τ则可以描述变量间的非线性相关性,其计算公式为

(2)

式中,xi、yi为第i个双变量样本值;n为样本数量;sign[·]为符号函数.

Copula分布的生成元及相关参数见表2.

表2 Copula分布的生成元及相关参数

具有最小AIC值[8]的Copula分布为最优分布,其计算公式为

(3)

式中,x1i、x2i分别为风速及波高的第i个样本值;f(x1i,x2i;θ)为样本点处联合概率密度值.

表3给出了不同Copula分布的RMSE及AIC值.如图2所示,当风速较小时,对应波高也较小且相对集中.随着风速的逐步增大,样本点分布更加分散.Copula分布显式表达式为

图2 Copula分布概率密度等高线

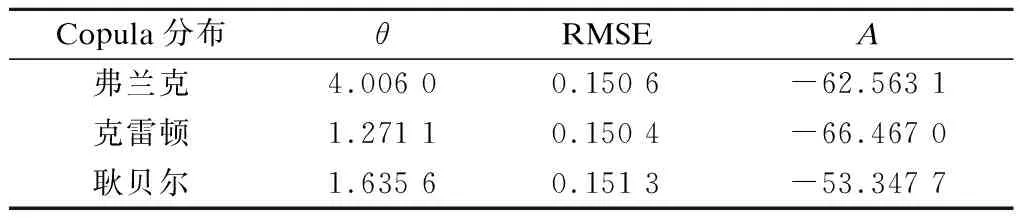
表3 Copula分布的RMSE及AIC值

(4)

式中,kHs、σHs、μHs分别为波高的形状参数、尺度参数和位置参数;kUw、σUw、μUw分别为风速的形状参数、尺度参数和位置参数.

1.3 联合回归周期

当单变量外部荷载X大于重现期对应的荷载值x时,重现期T(x)的计算公式为

(5)

式中,RT为荷载X的年回归率;F(x)为累积分布函数.

外部荷载为双变量时,若任一变量超过相应值, 则OR联合重现期TO(x,y)为

(6)

式中,C(x,y)为x和y的Copula分布.

双变量同时超过对应值时,AND联合重现期TA(x,y)为

(7)

选用AND联合重现期计算风速及波高在不同回归周期下的目标值,结果见表4.

表4 不同重现期风速波高组合值

2 荷载计算

2.1 横风荷载

体轴坐标系下,结构单位长度静风荷载为

(8)

式中,FH、FV、FM分别为阻力、升力及扭矩;CH、CV、CM分别为阻力系数、升力系数及扭矩系数;H和B分别为断面高度与宽度;ρair为空气密度;U为平均风速.

车桥气动力系数由XNJD-1风洞实验室获得[9],列车的阻力系数、升力系数及扭矩系数分别为1.478、0.231和0.239;桥梁的阻力系数、升力系数及扭矩系数分别为1.026、0.167和0.107.

2.2 波浪荷载

对于作用在小尺度桩柱上的波浪力,其对结构物的作用主要由黏滞效应和附加质量组成.作用于桩群上的单根桩柱波浪力可由拖曳力和惯性力构成[10-11],即

(9)

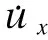
群桩结构还会产生遮蔽效应和干扰效应.考虑群桩系数K,作用在群桩上的总水平波浪力为

(10)

对于承台等大尺度结构物,应考虑绕射效应.根据文献[12],任意高度z处的顺波向波浪力为

(11)

3 车-桥耦合模型

选取平潭海峡某双塔斜拉桥为研究对象,该桥跨径组合为(133+196+532+196+133)m(见图3).图中,N01～N06为桥梁基础标号.本文采用CRH3型高速列车模型,8车编组,编组方式为M+T+M+T+T+M+T+M.车辆包括1个车体、2个转向架和4个轮对,共计7个刚体,通过一系弹簧、二系弹簧、减震器、抗侧滚扭杆等构件进行连接.每个刚体包含6个自由度,2个电机装配12个自由度,转臂定位8个自由度.单节动车模型共计62个自由度,拖车模型无电机装配,共计50个自由度.

图3 桥梁立面及构件截面图(单位:m)

通过ANSYS软件建立桥梁模型并进行子结构分析,获得质量矩阵、刚度矩阵、模态振型和节点坐标等信息.利用SIMPACK软件的前处理程序调用信息,生成FBI文件,从而将桥梁作为弹性体耦合集成到多体系统中.车桥系统的建模流程见文献[1-2],列车速度采用设计车速200 km/h.

4 实例分析

为充分研究横风和波浪对车桥动力响应的影响,除考虑风浪联合作用(WWVB)外,还对单风作用(WindVB)及单浪作用(WaveVB)下的系统响应进行分析计算.计算结果及指标限值[13-15]见表5.由表可以看出,工况3较工况1的横向位移增大了58.47%,横向及竖向加速度分别增大了9.38%和19.23%;车辆轮轴横向力增大了64.58%;脱轨系数增大了203.70%;轮重减载率增大了21.05%;横向及竖向加速度分别增大了36.08%和6.80%.工况6较工况4桥梁横向位移分别增大了58.20%;横向及竖向加速度分别增大了17.86%和17.33%.工况9较工况7桥梁横向位移、车辆轮轴横向力、车辆横向加速度增幅较小,均小于2%,其余指标均无变化.由此可知,桥梁及列车各响应指标均随风浪重现期的增大而增大.

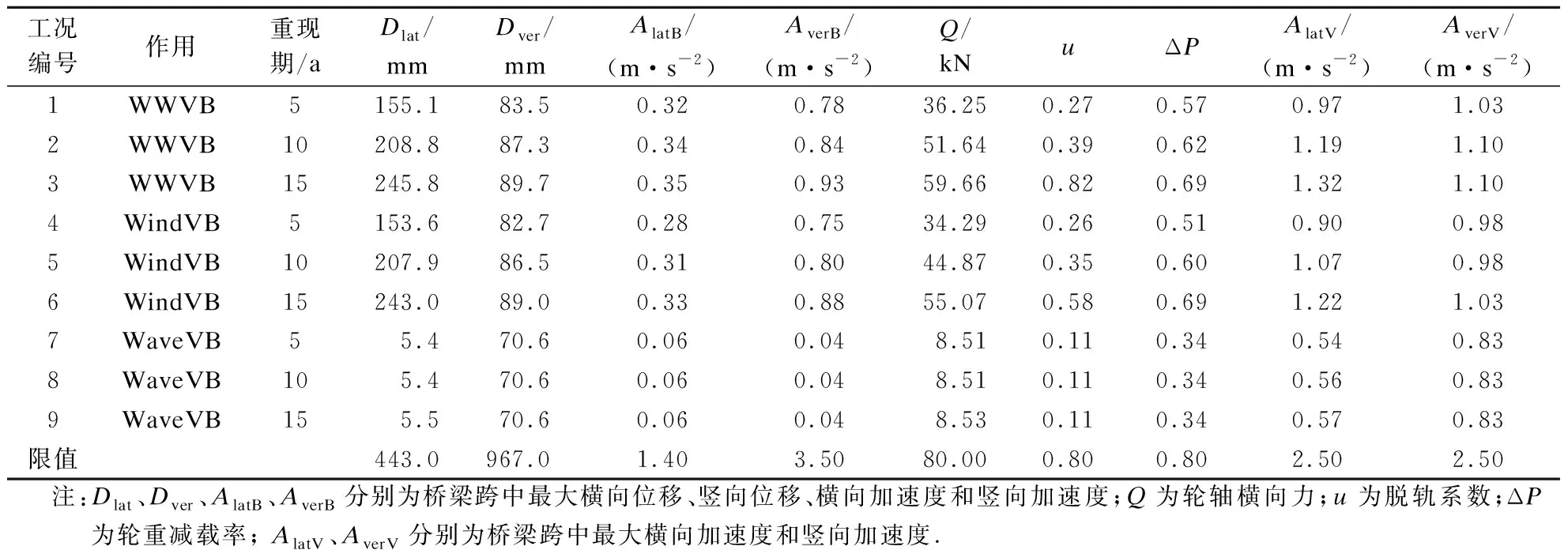
表5 车桥动力响应及限值

由图4可知,风浪联合作用于系统横桥向,故桥梁横向位移变化较为显著;而桥梁竖向位移主要由列车自重主导,横向风浪联合作用对竖向位移影响很小,随重现期的增加竖向位移增幅相对较小;在不同重现期下,桥梁各项动力指标均在安全限值之内.此外,波浪是一种周期性荷载,仅波浪荷载作用时,其对车辆响应影响较小;而当风浪联合作用时,这种周期性则会影响部分指标,对脱轨系数影响最大;总体上,仅工况3列车脱轨系数超出了限值(见图4(b)),其余列车指标均满足规范要求.

图4 不同重现期车桥响应

为研究风速和波高2个要素对车桥系统的影响,仅以5 a重现期下工况1、工况4及工况7为分析对象.

由表5可知,工况1桥梁的横向加速度、脱轨系数、轮重减载率分别为工况7的5.33、2.45、1.68倍,分别为工况4的1.14、1.04、1.12倍.由此可知,在风浪联合作用下,横风对车桥系统响应影响较大.由于波浪荷载作用于桥梁下部结构且桥下净空较大,其对系统响应影响相对较小.与仅横风作用时相比，风浪联合作用时桥梁横向加速度及轮重减载率增幅分别达到14%和12%,因而波浪荷载作用也不容忽视.