川西须家河组第二段深层致密气藏多层合采井产量递减劈分模型
2022-08-12詹泽东詹国卫黎华继胥德平
詹泽东, 郭 科, 詹国卫, 黎华继, 胥德平
(1.中国石油化工股份有限公司 西南油气分公司,成都 610041;2.成都理工大学 地球物理学院,成都 610059;3.成都理工大学 数学地质四川省重点实验室,成都 610059)
随着常规油气藏逐渐枯竭,非常规油气藏日益受到重视。深层致密气藏作为非常规油气藏的重要组成部分,具有埋藏深、储层致密、非均质性强、储层纵向叠置、单层产能低等特征[1],为提高气藏储量动用率和实现效益开发,通常采用多层合采的开发策略。多层合采开发技术的推广,虽然有效地提高了气井增储提效的能力,但却为气藏精细描述与气井单层产能评价带来了困难,因此如何开展多层合采井产量劈分,进而开展多层合采井单层产量预测与储量评价一直是国内外研究的热门课题[2-5]。多层合采井产量劈分的常用方法主要分为两类:一类是基于数学-物理模型的解析法,例如近年来王立等[2]提出的基于反距离加权插值法的产量劈分新方法;另一类是基于工程技术的直接测量方法,即利用生产测井直接获取各个层段的产量数据[6]。前者模型较为复杂,但实时性好;后者测量结果较为准确,但仅能反映各层的瞬时产量,且费用昂贵。本文以川西地区上三叠统须家河组第二段(简称“须二段”)深层致密气藏为研究对象,以Arps递减模型为理论依据[7],提出了深层致密气藏多层合采井产量的劈分新型数学模型。新模型具有简单、经济、适用的特点,进而为深层致密气藏多层合采井产量劈分提供了新思路与新方法,具有较强的实用性。
1 深层致密气藏产量递减特征
目前,川西须二气藏共有生产井26口,根据渗流理论开展气井流态诊断表明,其中20口井处于边界流状态[8-9],适合采用Arps递减模型开展产量递减分析。这20个(10口多层合采井)气井递减模型具有以下特征。
1.1 单层生产井整体遵循Arps递减模型
通过对川西须二气藏10口单层生产井产量递减模型诊断表明,在边界流条件下,气井遵循Arps递减模型,表明单层井递减指数为常数,典型井如A井(图1),即产量递减模型满足
(1)
式中:q(t)为气井产量(104m3/d);t为时间(d);q0为初始递减产量(104m3/d);D0为初始递减率(d-1);b为递减指数(无量纲)。当b→0时,产量递减模型称为指数递减模型,即
q(t)=e-D0t·q0
(2)

图1 典型井(A井)产量递减曲线Fig.1 Production decline curve of typical well (Well A)
1.2 多层合采井产量递减呈分段式
通过对川西须二气藏10口多层合采井产量递减模型诊断表明,在边界流条件下,气井产量递减趋势普遍具有分段式特征,即“拐点效应”,且可以采用Arps进行分段近似拟合,典型井如B井(图2、图3),表明递减指数不再是常数。
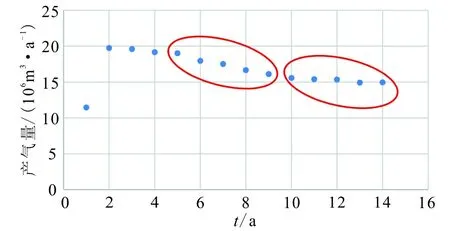
图2 多层合采井(B井)产量递减曲线Fig.2 Production decline curve for the multicompletion Well B

图3 多层合采井(B井)产量递减分段拟合图Fig.3 Sectional fitting diagram for the multicompletion Well B
1.3 多层合采井整体采用Arps递减曲线族拟合递减指数
通过对川西须二气藏10口多层合采井进行整体拟合表明,气井在进入边界流后递减指数普遍大于1,典型井如B井(图4),与产量积分曲线的有界性原理违背[10],表明深层致密气藏多层合采井不适合采用近似为单层井的拟合方式做产量递减分析。这就与Cheng Y.等[5]的主张不吻合。

图4 多层合采井(B井)整体拟合曲线Fig.4 Integral fitting curve of multicompletion well (Well B)
2 深层致密气藏多层合采井产量递减劈分模型
2.1 新模型的提出
气井处于边界流状态时,渗流状态处于拟稳态,多层合采井各层间不存在串层流动[11],气井产量满足质量守恒定律,即
(3)
式中:i为气层层序;n为层数;qi(t)为第i层产气量(104m3/d)。根据川西须二气藏气井产量递减特征,即单层生产井在边界流状态下满足Arps递减模型,即满足式(1),结合式(3),可以认为在边界流条件下,深层致密气藏多层合采井满足Arps递减模型的叠加模型
(4)
式中:q0i为第i层初始产量(104m3/d);D0i为第i层递减率(d-1);bi为第i层递减指数(无量纲)。
2.2 新模型的性质
根据J.J.Arps[7]对递减率与递减指数的定义,即
(5)
(6)
式中:D(t)为时刻t的瞬时递减率(d-1);b(t)为时刻t的瞬时递减指数(无量纲)。联立式(3)与式(5),得出新模型的递减率,即
(7)
式中:Di(t)为第i层在时刻t的产量递减率(d-1)。公式(7)表明,与单层生产井相比,多层合采井的递减率是随时间变化的,即为瞬时递减率,其数值为各层产量的加权平均,且权重是变化的。
联立式(3)、(6)和(7),得出多层合采井的递减指数为
(8)
公式(8)表明,与单层合采井递减指数为常数相比,多层合采井的递减指数是随时间变化的,即为瞬时递减指数,其数值与各层的产量及各层的瞬时递减率相关,这就是多层合采井采用近似模型拟合、递减指数出现大于1的异常特征的原因。
3 模型应用
3.1 正演递减模型特征
深层致密气藏由于储层纵向叠置,且层间非均质性强,最常见的情况就是一个高渗层与低渗层的纵向组合关系,因此分析双层合采模型产量递减特征响应对于明确气藏递减行为具有重要意义。
根据川西油气开发实践与渗流理论,高渗层通常具有较大的初始产量与初始递减率;低渗层由于储层更加致密,供气能力较差,因此具有较大的递减指数。据此,设定模型参数如表1。

表1 高渗层、低渗层模型参数Table 1 Parameters for layers with high and low permeability
将模型参数代入公式(4)、(5)和(6),合成双层模型气井递减模型如图5。

图5 合成井记录Fig.5 Synthetic well record
从产量-时间关系图(图5-A)可以看出,针对高、低渗透组合模型,气井产量前期主要受高渗层影响,其递减趋势与高渗层的递减趋势保持一致;后期以低渗层为主导,合成记录逼近低渗层的产量递减模型。从递减速率-时间关系图(图5-B)可以看出,合成记录瞬时递减率位于高、低渗层递减率之间,前期逼近高渗层,晚期逼近低渗层。从递减指数-时间关系图(图5-C)可以看出,合成记录的瞬时递减指数不再为常数,其数值先递增再递减最后逼近于低渗层,这也是多层合采井递减指数大于1的原因。
3.2 利用“拐点效应”判别气井多层供气特征
以表1中的双层合采井为例,通过改变低渗层的递减模型参数,合成气井产量记录(图6)。
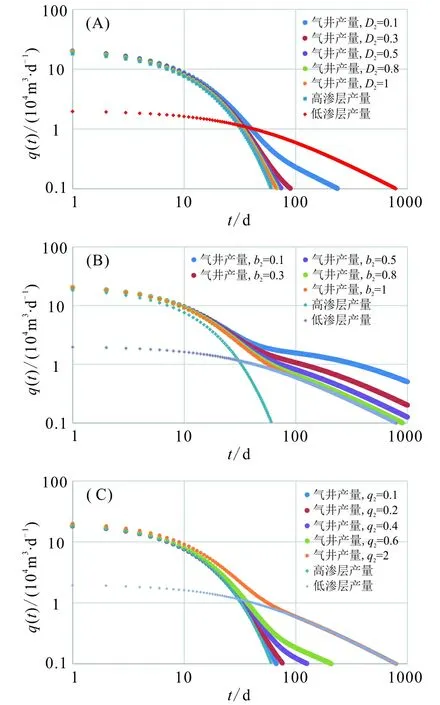
图6 低渗层不同递减参数对合成记录形态的影响Fig.6 Effects of different decline parameters of low permeability layer on the morphology of synthetic records
从图6可以看出,多层合采井普遍存在“拐点效应”,因此在气井正常生产情况下,可以利用“拐点效应”识别多层合采井,进而提供了气井在储层纵向多层分布条件下是否存在连通合采现象;但“拐点效应”受低渗层的递减模型参数影响较大,主要表现为低渗层初始递减率越低,递减指数越小,初始递减产量越高,“拐点效应”越明显。
3.3 反演产量劈分与储量评价
3.3.1 模型的求解
根据新模型原理与理论推导,事实上具有四大守恒方程,即质量守恒、递减率加权守恒、递减指数加权守恒、储量守恒,即由式(3)—式(8)分别整理得

(9)
(10)
f3(q0i,bi,D0i):q(t)D2(t)[1+b(t)]-
(11)
f4(q0i,bi,D0i):
(12)
其中:
(13)
(14)
(15)
(16)
Gp(t)表示t时刻气井累计产量(104m3)。
令

(17)
则多层合采模型产量劈分问题转化为最优化问题,根据最小二乘法原理与最优化原理[12],则
(18)
求解方程组(18)的解,即为各层的产量递减模型参数。
3.3.2 应用实例
一方面,对23口双层合采井递减期进行生产测井的测试结果与使用新模型的分解结果回归分析表明,新模型分解的产量比(主产层/次产层)与生产测井线性回归系数接近1且相关系数达到0.98,表明新模型对递减期的气井产量分解较为真实可靠,可近似代替生产测井,对气藏开发评价降本增效具有实际意义(图7)。

图7 川西地区双层合采井递减期生产测井与新模型产量劈分比回归分析图Fig.7 Regression analysis of production logging and productivity split ratio of new model in decline period of double-layer combined production wells in western Sichuan
一方面,采用方程组(18)对川西某处于边界流的双层合采井利用计算机编程求得各层的产量劈分模型(图8)分别为

(19)

(20)

图8 合采井C井产量劈分模型成果图Fig.8 Production split for combined producing for Well C with two gas layers
根据拟合的分层递减模型,按Arps递减模型[7]分别计算各层的动态储量,结果分别为2.4×108m3、1.8×108m3,与第一层、第二层单层开采井采用Blasingame典型曲线[13]计算的平均单井动态储量(分别为2.2×108m3、1.72×108m3)相当,表明采用新模型不仅可以劈分产量,也可以有效开展动态储量评价。而根据Cheng Y.等[5]的理论,以近似单层井采用Arps递减模型拟合,其产量递减模型为式(21),递减指数大于1[式(21)],无法计算该井动态储量。所以本文的新模型具有优越性。
双层合采:
(21)
从产量递减特征分析,采用新模型劈分的分层产量递减特征与第一层、第二层单层开采井产量递减特征一致(第一层产量递减快、第二层产量缓慢递减),进一步表明新模型劈分产量的可靠性与适用性(图 9)。

图9 第一层、第二层单层开采井产量递减曲线Fig.9 Production decline curve of the first and second single-layer producing wells
4 结 论
a. 以川西须二气藏产量递减分析为基础,建立了深层致密气藏多层合采井产量递减劈分数学模型,通过理论推导与分析,明确了该模型具有“产量加权”“瞬时递减率”“瞬时递减指数”三大特征。
b. 根据新模型的性质特征,建立了基于四大守恒方程的多层合采井产量劈分模型的最优化求解各层产量递减模型参数的数学模型。
c. 将新模型应用于开发实践,不仅可以有效劈分多层合采井的产量,同时可以评价各层动态储量。理论计算与实际开发较为吻合,表明该模型具有较强的可靠性和实用性,进而为模型正演与反演的应用以及在一定程度上取代生产测井提供了新方法、新技术。
