珩磨缸套表面粗糙度预测及多目标优化研究

吕延军 ,李 杰 ,强 程 ,李鹏洲 ,张永芳 ,常 欢

(1.西安理工大学 机械与精密仪器工程学院,陕西 西安 710048;2.西安交通大学 机械制造系统工程国家重点实验室,陕西 西安 710049;3.西安理工大学 印刷包装与数字媒体学院,陕西 西安 710054)

近年来，随着国际环保标准的不断提高，低油耗和低排放发动机受到广泛关注.内燃机缸套作为内燃机的核心部件，其加工质量的优劣直接影响发动机的性能[1-5].为了提高燃油效率，内燃机缸套内孔表面应具有优良的耐磨性、低摩擦和较好的保油性能，以减少油耗和磨合时间，这使得缸套珩磨的表面质量控制成为目前缸套加工的主要问题之一.如果能在缸套珩磨加工前对其表面质量进行预测并对珩磨加工参数有目地进行优化，就可以在一定程度上提高内燃机缸套的珩磨加工效率以及经济性.

目前国际上通常采用基于Abbott-Firestone曲线的Rk粗糙度参数集[6]评价缸套表面加工质量，因此对Rk粗糙度参数集进行建模和预测并分析各加工参数对珩磨加工质量的影响，近年来受到国内外学者的广泛关注.人工神经网络(Artificial neural network,ANN)与响应面法(Response surface methodology,RSM)可有效解决线性和非线性多元回归问题，基于ANN和RSM对加工质量预测模型进行建模，可建立加工参数与表面加工质量之间的映射关系，因此国内外学者进行了一系列相关研究[7-12].Thankachan等[13]研究不同加工工艺参数对电火花线切割铝合金和金属基复合材料的材料去除率(Material removal rate,MRR)和表面粗糙度(Ra)的影响时，建立ANN模型预测了MRR和Ra值，并验证了模型的有效性.Yang等[14]依据激光切割AL6061T6合金时切割区域温度和表面粗糙度的试验结果，以切削速度、激光功率、板材厚度和辅助气压为输入参数，以表面粗糙度和切削温度为目标属性，建立了ANN预测模型，并验证了模型的准确性.Hanief等[15]建立了ANN模型预测磨合过程中的表面粗糙度，采用统计学方法[决定系数R2及均方误差(Meansquare error，MSE)和平均绝对百分比误差(MAPE)]验证了预测结果的有效性.Sadizade等[6]借助RSM分析了不同珩磨加工参数对Rk粗糙度参数集的影响，并采用合意性函数对加工参数进行了两目标优化以达到粗糙度与加工时间最优.赵胜军等[16]借助RSM建立了球栅阵列(Ball grid array，BGA）无铅焊点再流焊焊后残余应力的回归方程模型，并采用响应面-遗传算法对焊点结构参数进行优化，获得最优结构参数.郑玲等[17]运用二次多项式响应面法获得了橡胶主簧动特性关于幅值和频率的回归方程，建立了集总参数动态修正模型，借助该模型分析了半主动悬置幅变动特性的产生机理.郑昱等[18]应用响应面法构建了二阶响应面模型，从而对九索在框架上的安装位置及在动平台上下表面的连接位置进行优化设计，获得了能使工作空间最大且沿竖直方向分布最均匀的优化结果.Moghaddas[19]借助RSM以及方差分析法研究了钻孔参数(包括主轴转速、进给速度和振幅)对铝合金表面粗糙度等参数的影响，并得到了最优钻进参数.Buj-Corral等[20]基于响应面法对珩磨缸套表面光洁度和MRR进行了建模，分析了加工参数对两目标的影响，并得到最优加工参数.Asiltürk等[21]为了研究不同车削参数(速度、进给量和切削深度)对表面粗糙度的影响，采用ANN和RSM对AISI 1040钢表面粗糙度进行建模，并采用全因子试验进行模型验证.Bhatti等[22]借助ANN和RSM预测模型研究了电絮凝系统对合成废水中铜的去除效果，并基于遗传算法进行多目标优化，获得了参数优化结果的Pareto前沿.

综上所述，借助ANN和RSM方法对加工表面粗糙度预测与加工参数优化获得了很好的效果.为了提高内燃机的燃油效率和经济性，对内燃机珩磨缸套表面粗糙度的预测与加工参数优化显得尤为重要.为了对缸套珩磨表面粗糙度进行预测并对加工参数进行优化，本文中基于广义回归神经网络(Generalized regression neural network，GRNN)与基于BBD (Box-behnken design)试验设计法的响应曲面法建立预测模型，对粗珩阶段缸套表面粗糙度核心粗糙度Rk、简约峰高Rpk和简约谷深Rvk进行预测，并用试验验证预测模型的有效性.同时，结合三维响应曲面分析加工参数单个因素以及多个因素交互作用对表面粗糙度的显著影响.在此基础上，结合建立的粗糙度预测模型与NSGA-Ⅱ算法进行多目标优化，获得粗糙度多目标优化后的Pareto前沿，为缸套粗珩阶段提供更多的加工工艺参数组合.

1 试验设计

1.1 试验设备

为了获得多组不同珩磨加工参数下的缸套表面粗糙度，在某厂内燃机缸套加工流水线的珩磨机床[图1(a)]上进行珩磨加工试验，测量不同珩磨加工参数下的表面粗糙度.试验过程中，主要珩磨加工参数为珩磨头的往复速度、旋转速度和珩磨压力.加工对象为某型号气缸套，内径230 mm，材料为特种铸铁，如图1(b)所示.珩磨油石及其安装位置如图1(c)所示，油石材质为SiC，油石粒度为80，油石的安装方式为两条油石组成1个油石组，其中单根油石尺寸为13 mm×15 mm×150 mm，油石组的尺寸为13 mm×15 mm×300 mm.在完成缸套的珩磨加工后，采用HOMMEL TESTER T1000 (20 W)粗糙度检测仪[图1(d)]测量被加工缸套内表面的粗糙度，输出核心粗糙度深度(Rk)、简约峰高(Rpk)和简约谷深(Rvk)等粗糙度相关参数，测量误差可保持在3%以内.试验设备如图1所示.

Fig.1 Test equipments图1 试验设备

1.2 缸套表面粗糙度评定参数(Rk、Rpk和Rvk)

在国际标准中，粗糙度的评定参数常用的有轮廓平均算术偏差Ra与不平度平均高度Rz，但是由于不同特征的表面可能产生相同的Ra值，测量过程中如果存在极端的表面会导致数据Rz不准确，或1个表面被重复测量数次，表面上测点不同可能引起结果的变化.由于Ra和Rz不足以精确评价缸套珩磨表面形貌，所以通常采用Rk粗糙度参数集评定缸套珩磨后的表面形貌.该参数集属于德国DIN 4 776标准，主要用于表征具有高应力的表面，如珩磨表面、抛光表面及磨削表面等.根据被加工缸套的使用特性，试验中选择以下粗糙度评定参数作为缸套内孔表面的粗糙度特性参数，如图2所示：Rk(核心粗糙度深度)、Rpk(简约峰高)和Rvk(简约谷深).

Fig.2 Schematic diagram of parameter set of Rk roughness图2 Rk粗糙度参数集示意图

1.3 试验设计及测量结果

由于缸套珩磨过程所涉及的加工参数较多，因此结合实际加工环境设计三因素三水平全因子试验，三因素分别为珩磨压力占比P(%)、珩磨头的往复速度VRe(m/min)和珩磨头的旋转速度VR(r/min)，其中珩磨机总压力为5 MPa，每个因素有3个水平，试验的响应参数分别为Rk、Rvk和Rpk，设计因素和水平组合列于表1中.

表1 粗珩阶段试验设计因素和水平Table 1 Factors and level of experiment design in rough honing

为了验证预测模型的有效性，针对神经网络模型，从27组试验数据中取21组数据作为训练样本，6组样本作为测试样本.将表2数据中第1～7组、10～16组和19～25组作为训练样本；第8、9、17、18、26和27组作为测试样本，测试样本及结果列于表3中.表3中的测试样本也可以用于检验基于响应曲面法建立的回归模型的有效性.

表2 试验设计及结果Table 2 Parameters and results of experiments

表3 测试样本Table 3 Test samples

2 基于神经网络的表面粗糙度预测

在已知珩磨加工参数的基础上，为了实现珩磨缸套表面粗糙度的准确预测，运用神经网络方法建立加工参数(珩磨压力、珩磨头的往复速度和珩磨头的旋转速度)与缸套表面核心粗糙度深度Rk、简约峰高Rpk和简约谷深Rvk之间的非线性映射关系，从而进行珩磨缸套表面粗糙度的预测.采用广义回归神经网络(Generalized regression neural network,GRNN)建立珩磨缸套表面粗糙度预测模型，模型的性能评价指标采用均方误差和决定系数R2.

2.1 表面粗糙度的GRNN预测模型

广义回归神经网络GRNN是径向基神经网络(Radial basis function，RBF)的一种，具有优异的非线性映射能力和柔性网络结构以及高度的容错性和鲁棒性.GRNN网络结构由4层构成，分别为输入层、模式层、求和层和输出层.GRNN的拓扑结构如图3所示.

2.2 采用K折交叉验证法进行光滑因子的优选

GRNN的建模主要需要3个参数，分别为网络输入、网络输出和光滑因子 σ.因为GRNN不需要训练，所以光滑因子σ (也称为spread，是径向基函数的扩展速度)是建立该网络模型所需要确定的重要参数，GRNN模型的建立本质上就是对光滑因子 σ进行优选.本文中采用5折交叉验证的方法对GRNN的光滑因子进行优选.图4示出了5折交叉验证算法示意图.

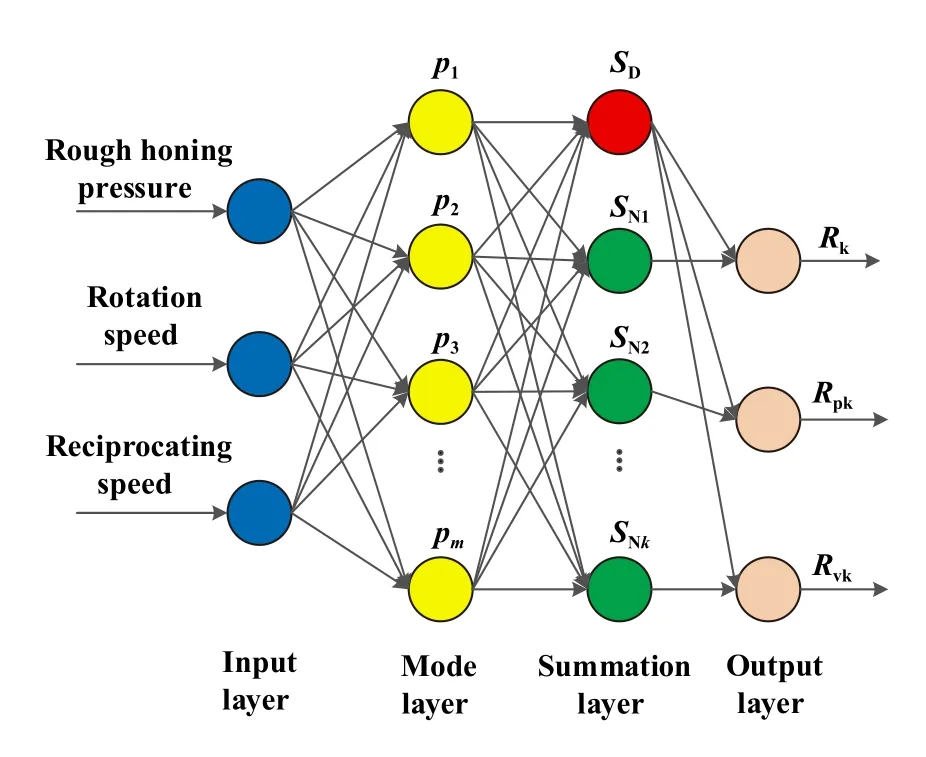
Fig.3 Topography of generalized regression neural network (GRNN)图3 广义回归神经网络(GRNN)拓扑结构图

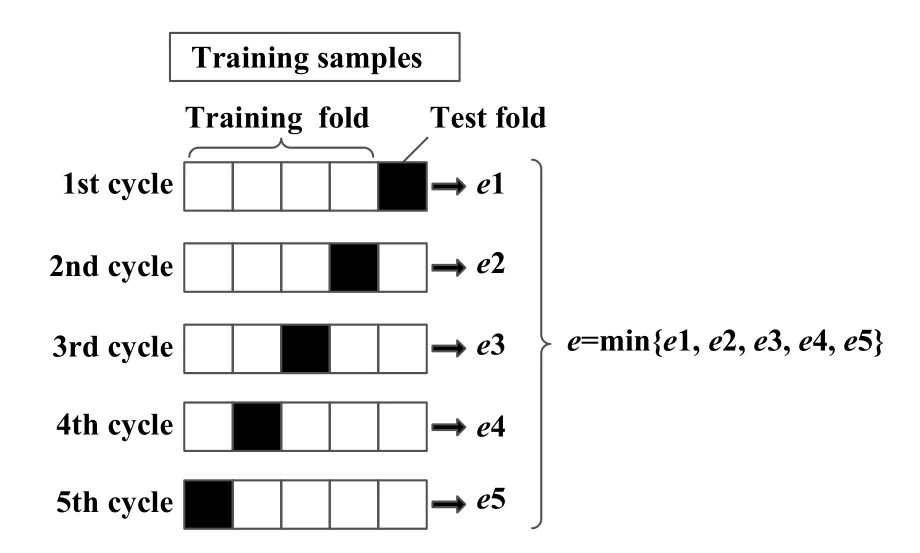
Fig.4 Schematic diagram of 5-fold cross validation algorithm图4 5折交叉验证算法示意图

每次交叉验证中，通过改变光滑因子spread的取值可以在很大程度上影响网络的预测性能，在5次交叉验证过程中找到最小的MSE，进而确定产生最小MSE的spread值，从而实现网络参数的优选.5折交叉验证时，不同spread取值对神经网络均方误差MSE的影响如图5所示，当MSE最小时，spread值为0.01.

2.3 表面粗糙度预测

将训练好的GRNN预测模型用于珩磨缸套表面的粗糙度预测，预测对象为6组测试样本(表3).图6示出了GRNN预测模型的粗糙度预测值与实测值的对比关系.从对比图中可以看出，粗糙度的预测值与实测值之间的误差整体较小，表明了GRNN预测模型具有很好的拟合效果.

3 基于响应曲面法的表面粗糙度预测

3.1 试验设计及测量结果

由于缸套珩磨过程中涉及的加工参数较多，本文中采用响应面法设计了三因素三水平试验，试验的因素和水平列于表4中.采用响应面法中的Box-behnken design (BBD)[23]法设计试验，试验设计和结果列于表5中.

表4 粗珩阶段试验设计因素和水平Table 4 Factors and level of experiment design in rough honing

表5 BBD试验设计及结果Table 5 Experimental parameters and results of BBD

3.2 基于响应曲面法建模

运用响应面法建立珩磨缸套表面Rk粗糙度参数集与各主要加工参数之间的响应关系，为之后的粗糙度预测以及加工参数的优化建立回归模型.

采用响应面法建立加工参数与粗糙度Rk、Rpk和Rvk之间的函数关系，运用带交叉项的二阶模型[24]进行描述，二阶模型表示为

式中：Y为响应结果；β0为常数项，βi为一次项的回归系数，βii为二次项的回归系数，βij为交互项的回归系数；xi和xj为因素变量，ε为试验的误差项.

3.2.1 表面粗糙度Rk建模及分析

(1) 方差分析

试验数据进行方差分析，选择置信水平为95%，粗糙度Rk回归模型的方差分析结果列于表6中，其中A、B和C分别表示三因素，即珩磨压力、往复速度和旋转速度.

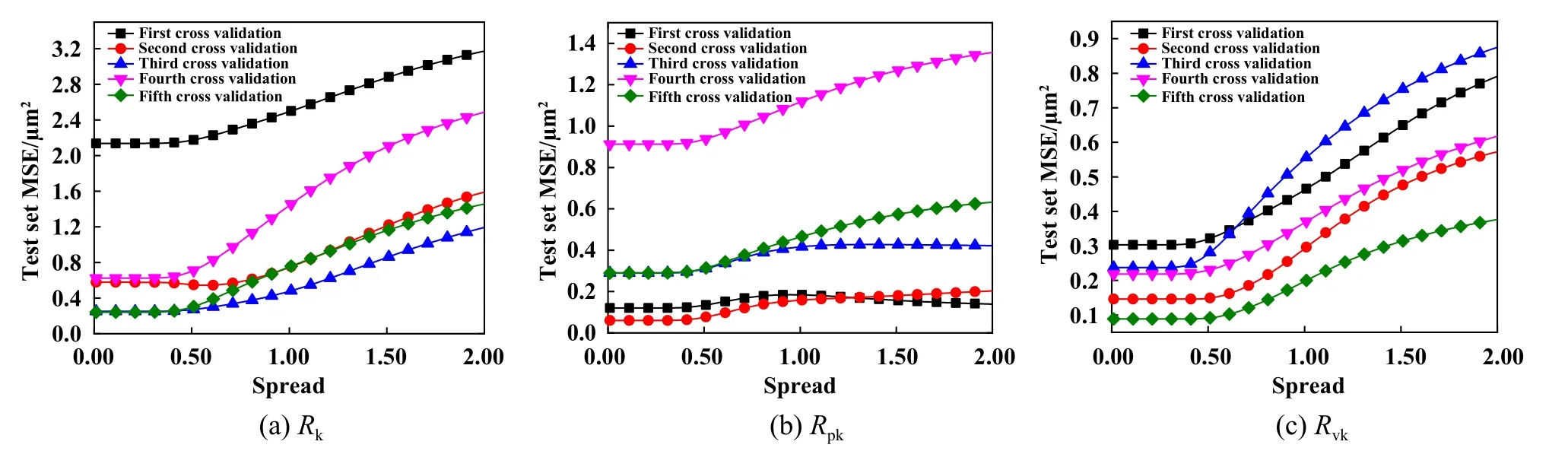
Fig.5 Influence of spread on MSE of prediction network图5 Spread取值对预测网络MSE的影响

Fig.6 Comparison between predicted and measured roughness based on GRNN model图6 基于GRNN模型的粗糙度预测值与实测值对比图

方差分析也叫F检验，用来评估组间差异，F越大，表示方程越显著，拟合程度越好.P值表示不拒绝原假设的程度，用来评价模型中各个项的显著性，P值小于0.05，表示该项是显著项，即对模型的影响比较大，P值小于0.01，表示极其显著.由表6可以知道，模型的P值为0.000 1 (P＜0.01)，则表示模型极其显著，模型的失拟项(Lack of fit)的P值为0.198 4 (P＞0.05)，表明失拟不显著，由结果可知建立的回归模型具有很好的拟合效果.

表6 粗糙度Rk回归模型的方差分析Table 6 Variance analysis of Rk regression model

(2) 模型分析

二阶模型的学生化残差正态概率如图7所示，由图7可分析出，残差点的分布趋于直线，这意味着数据符合正态分布且无大的偏差.

试验次序与学生化残差关系如图8所示，学生化残差点沿着横坐标零线上下均匀分布，且没有孤立和缺失的点出现.该模型的决定系数为0.973 4，说明模型对试验结果的预测程度较高，结合图7和图8可知该模型描述珩磨缸套表面粗糙度Rk随加工参数变化趋势的可信度较高.

(3) 响应面分析

此粗糙度预测模型中响应曲面图形是各试验因子(P、VRe和VR)中有1个因子的数值固定为中等水平，即0水平时，其余两因子与响应值所构成的三维空间的曲面图.Rk粗糙度预测模型三维响应面及其等高线如图9所示.

由图9可知，粗糙度Rk值在2.56～8.20 μm之间变化.由图9(a)和9(b)可以看出：其他条件不变，珩磨压力P从30%增至40%左右时，Rk值逐渐减小；P从40%增至50%左右，Rk值又逐渐增大，尤其旋转速度VR为35 r/min时变化最为明显，因此珩磨头的珩磨压力P对粗糙度Rk值的影响程度较大.由图9(a)和9(c)可以看出：其他条件不变，往复速度VRe从12 m/min增至13 m/min左右时，Rk值略微减小；VRe从13 m/min增至14 m/min时，Rk值又略微增大，因此珩磨头的往复速度VRe对粗糙度Rk值的影响程度不大.由图9(b)和9(c)可以看出：其他条件不变，旋转速度VR从30 r/min增至35 r/min左右时，Rk值略微增大；VR从35 r/min增至50 r/min时，Rk值又逐渐减小，尤其VR从40 r/min增至50 r/min时，Rk值急剧下降，因此珩磨头的旋转速度VR对粗糙度Rk值影响程度较大.结合表4中各因素的F统计量可知：各因素对珩磨缸套表面粗糙度Rk的影响显著性顺序为珩磨头旋转速度VR＞珩磨压力P＞珩磨头往复速度VRe.

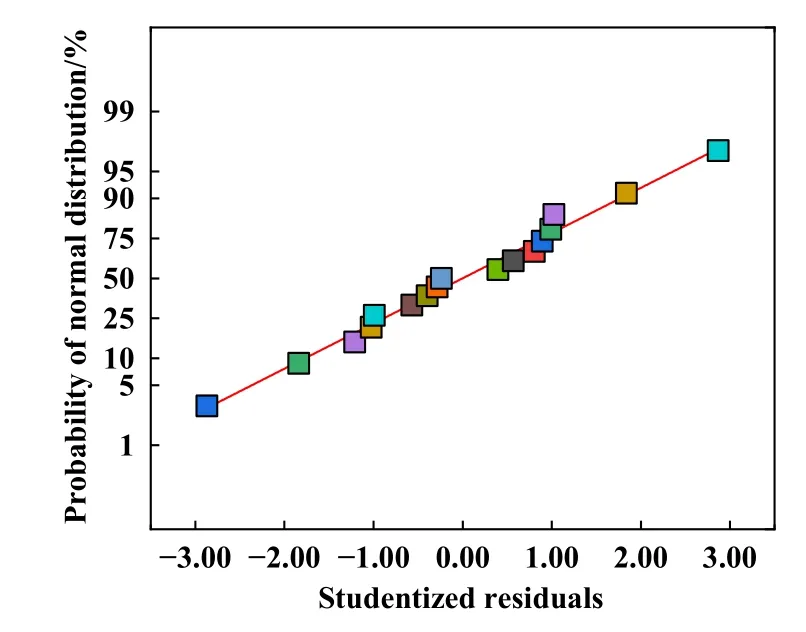
Fig.7 Normal probability of studentized residuals for second order model图7 二阶模型的学生化残差正态概率

Fig.8 Relationship between test sequence and studentized residual图8 试验次序与学生化残差关系图

3.2.2 表面粗糙度Rpk建模及分析

(1) 方差分析

对试验数据进行方差分析，选择置信水平为95%，粗糙度Rpk回归模型的方差分析结果列于表7中.由表7可以看出此二阶模型是显著的，失拟项的P值为0.322 6，远大于0.05，表明失拟不显著，建立的回归模型具有很好的拟合效果.

Fig.9 Three-dimensional response surface and contour of Rk roughness prediction model图9 Rk粗糙度预测模型三维响应面及等高线

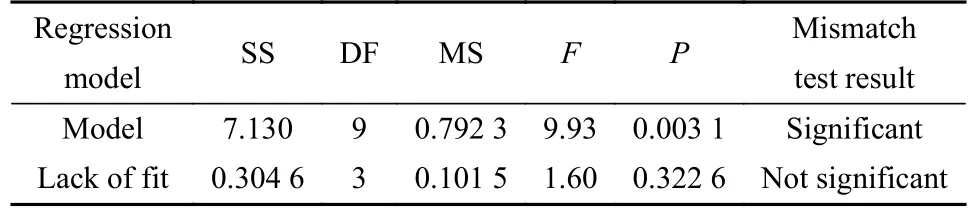
表7 粗糙度Rpk回归模型的方差分析Table 7 Variance analysis of Rpk regression model

(2) 模型分析

该模型的决定系数为0.927 4，说明模型对试验结果的预测程度较高.图10示出了二阶模型的学生化残差正态概率图，图11示出了试验次序与学生化残差关系图，结合图10～11可知该模型描述珩磨缸套表面粗糙度Rpk随加工参数变化趋势的可信度较高.

(3) 响应面分析

Rpk粗糙度预测模型三维响应面及其等高线如图12所示.由图12可知：粗糙度Rpk值在0.82～3.26 μm之间变化.由图12(a)和12(b)可分析出：其他条件不变，珩磨压力P从30%增至50%时，Rpk值显著增大，因此珩磨头的珩磨压力P对粗糙度Rpk值的影响程度大.由图12(a)和12(c)可分析出：其他条件不变，往复速度VRe从12 m/min增至13 m/min左右时，Rpk值略微减小；VRe从13 m/min增至14 m/min时，Rpk值又略微增大，因此珩磨头的往复速度VRe对粗糙度Rpk值的影响程度不大；由图12(b)和12(c)可以看出：其他条件不变，旋转速度VR从30 r/min增至40 r/min左右时，Rpk值逐渐增大；VR从40 r/min增至50 r/min时，Rpk值逐渐减小，因此珩磨头的旋转速度VR对粗糙度Rpk值影响程度较大.结合方差分析后各因素的F统计量可知：各因素对珩磨缸套表面粗糙度Rpk的影响显著性顺序为珩磨压力P＞珩磨头旋转速度VR＞珩磨头往复速度VRe.

Fig.10 Normal probability of studentized residuals for second order model图10 二阶模型的学生化残差正态概率图

Fig.11 Relationship between test sequence and studentized residual图11 试验次序与学生化残差关系图

3.2.3 表面粗糙度Rvk建模及分析

(1) 方差分析

对试验数据进行方差分析，选择置信水平为95%，粗糙度Rvk回归模型的方差分析结果列于表8中.由表8可知此二阶模型是显著的，失拟项的P值为0.137 2，远大于0.05，表明失拟不显著，建立的回归模型具有很好的拟合效果.

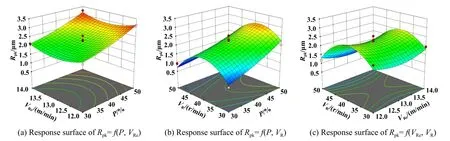
Fig.12 Three-dimensional response surface and contour of Rpk roughness prediction model图12 Rpk粗糙度预测模型三维响应面及等高线

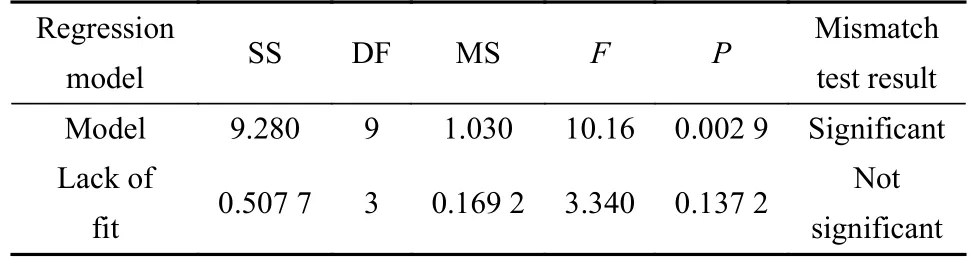
表8 粗糙度Rvk回归模型的方差分析Table 8 Variance analysis of Rvk regression model

(2) 模型分析

该模型的决定系数为0.928 9，说明模型对试验结果的预测程度较高.图13示出了二阶模型的学生化残差正态概率图，图14示出了试验次序与学生化残差关系图，结合图13和图14可以得出该模型能描述珩磨缸套表面粗糙度Rvk随加工参数变化趋势的可信度较高.

(3) 响应面分析

Rvk粗糙度预测模型三维响应面及其等高线如图15所示.由图15可知：粗糙度Rvk值在2.07～4.72 μm之间变化.由图15(a)可以看出：其他条件不变，珩磨压力P从30%增至50%时，Rvk值显著增大.由图15(b)可以看出：其他条件不变，旋转速度VR从30 r/min增至45 r/min左右且珩磨压力P从30%增至50%时，Rvk值逐渐增大，且增幅较大；旋转速度VR从45 r/min增至50 r/min且珩磨压力P从30%增至50%时，Rvk值基本保持不变，因此珩磨头的珩磨压力P对粗糙度Rvk值影响程度大.由图15(a)和15(c)可以看出：其他条件不变，往复速度VRe从12 m/min增至14 m/min时，Rvk值稍有增大，整体趋势较为平缓，因此珩磨头的往复速度VRe对粗糙度Rvk值影响程度不大.由图15(b)和15(c)可知：其他条件不变，旋转速度VR从30 r/min增至38 r/min时，Rvk值略微增大；VR从38 r/min增至50 r/min时，Rvk值逐渐减小，因此珩磨头的旋转速度VR对粗糙度Rvk值影响程度较大.结合方差分析后各因素的F统计量可知：各因素对珩磨缸套表面粗糙度Rvk的影响显著性顺序为珩磨压力P＞珩磨头旋转速度VR＞珩磨头往复速度VRe.

Fig.13 Normal probability of Studentized residuals for second order model图13 二阶模型的学生化残差正态概率图

Fig.14 Relationship between test sequence and studentized residual图14 试验次序与学生化残差关系图

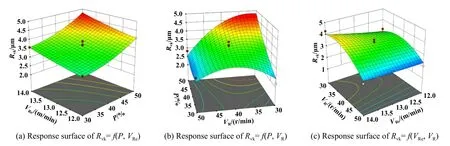
Fig.15 Three-dimensional response surface and contour of Rvk roughness prediction model图15 Rvk粗糙度预测模型三维响应面及等高线

3.3 表面粗糙度回归模型优化

3.3.1Rk回归模型优化

为进一步提高预测精度，通过消除非显著项的方法使模型具有更高的预测精度，由表6中数据可知，模型中有很多非显著项，这些非显著项会影响模型的预测精度，因此需要对模型进行优化，得到最优的二阶模型.由表6可知，模型中的AB、AC和BC项的P值远大于0.05，因此在消除这些非显著项的同时增加其他交互项来提高模型精度.通过消除AC项，增加交互项A2B，模型的显著性以及失拟项的显著性都得到了很大的改善，提高了模型的预测性能.表9列出了优化前后Rk回归模型的预测精度.

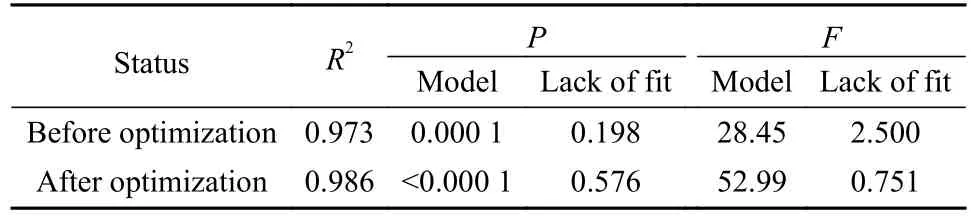
表9 优化前后Rk回归模型的预测精度对比Table 9 Comparison of prediction accuracy of Rk regression model before and after optimization

针对三因素构建回归方程以预测粗糙度，经过对模型中的非显著项进行消除并增加新的交互项之后，得到的表面粗糙度Rk的回归模型方程式为

3.3.2Rpk和Rvk回归模型优化

对表面粗糙度Rpk和Rvk也进行模型优化，得到优化后的预测模型.

(1)Rpk回归模型的优化

消除原二阶模型的AB和BC项，增加A2C项，优化后的回归模型方程式为

(2)Rvk回归模型的优化

消除原二阶模型的B2项，增加A2C项，优化后的回归模型方程式为

3.4 表面粗糙度预测

采用优化的回归模型预测珩磨缸套表面的粗糙度.预测对象为6组测试样本，数据列于表3中，优化模型的预测值与实测值的对比如图16所示.

从对比图中可以看出，粗糙度的预测值与实测值之间的误差整体较小，说明拟合效果较好.

3.5 预测结果分析与讨论

图17示出了基于GRNN与RSM多元回归模型的预测性能评价指标对比关系：从图17中的性能评价指标可以看出，两种预测模型预测的结果与试验结果均具有很好的一致性.GRNN预测模型预测结果的决定系数R2的均值为0.959，RSM多元回归预测模型的决定系数R2的均值为0.963.GRNN预测模型预测结果的均方误差MSE的均值为0.054，RSM多元回归预测模型的均方误差MSE的均值为0.089.说明两种预测模型的可信度均较高.

4 基于带精英策略的非支配排序遗传算法(NSGA-II)的Pareto多目标优化问题

由于精珩是在粗珩加工后进行，所以粗珩加工后表面粗糙度值应该尽可能小，这样才能使精珩加工获得更好的表面质量.缸套内表面的粗糙度评价参数Rk、Rpk和Rvk，会伴随着每一次的加工而产生，因此选择合适的加工参数使得Rk、Rpk和Rvk均相对最小显得尤为重要.对Rk粗糙度参数集进行多目标优化是为了获得粗糙度集的Pareto最优前沿(简称为Pareto前沿).

Fig.16 Comparison of measured roughness and predicted roughness based on RSM multiple regression model图16 基于RSM多元回归模型的粗糙度预测值与实测值对比图

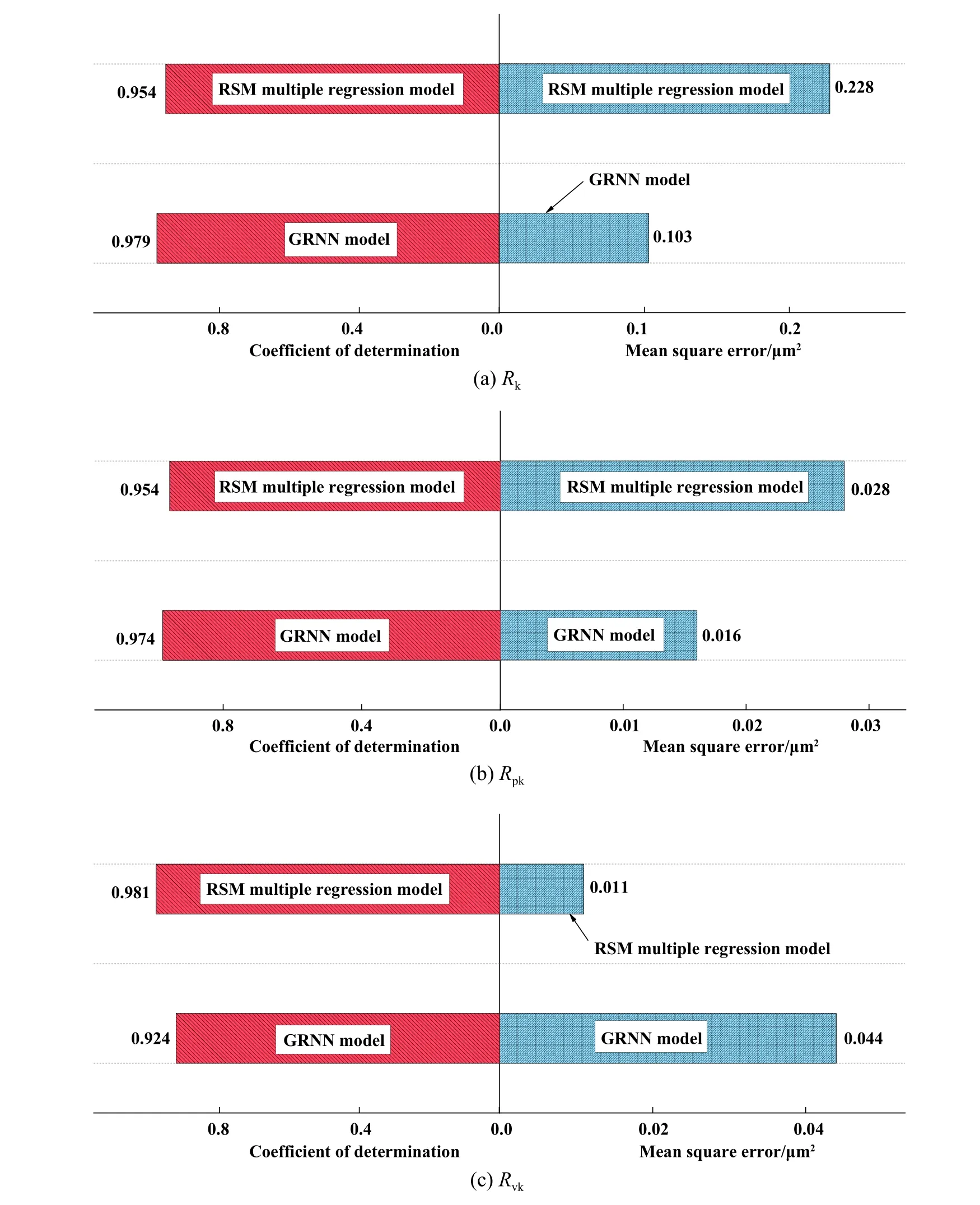
Fig.17 Comparison of evaluation indexes of prediction performance of GRNN and RSM models图17 GRNN模型与RSM多元回归模型预测性能的评价指标对比图

多目标优化问题[25]可表示为式

式中：x∈X⊂Rn，F(x)∈Y⊂Rm.x和F(x)分别是决策向量和目标向量，X和Y分别是决策空间和目标空间，Rn为决策向量集合，个数为n，Rm为目标向量集合，个数为m.gi(x)为对决策空间进行约束的p个不等式函数，hj(x)为对决策空间进行约束的q个等式函数，约束函数共同决定决策向量的可行域.

基于Pareto占优思想的多目标优化算法中，带精英策略的非支配排序遗传算法NSGA-Ⅱ(Non-dominated Sorting Genetic Algorithm Ⅱ)是最有效的算法之一.该方法运行速度快，解集收敛性好，本文中采用NSGA-Ⅱ优化算法进行粗糙度集的多目标优化.

4.1 缸套表面粗糙度两目标优化

采用NSGA-Ⅱ算法对粗糙度Rk、Rpk和Rvk进行两目标同步优化，目标函数为已求得的优化后的RSM多元回归模型.对粗糙度Rk、Rpk和Rvk中任意两个目标进行两目标同步优化，优化目标时两者的值同时相对最小，即无更优解使得两个目标中的1个目标值减小的同时，另一目标值不增大.为了获得粗糙度两目标优化的相对最小值，需寻求决策向量珩磨压力P、珩磨头的往复速度VRe和珩磨头的旋转速度VR的最优参数组合.NSGA-Ⅱ算法里的初始种群数设为100，迭代次数为100次.图18示出了优化结果的Pareto前沿.

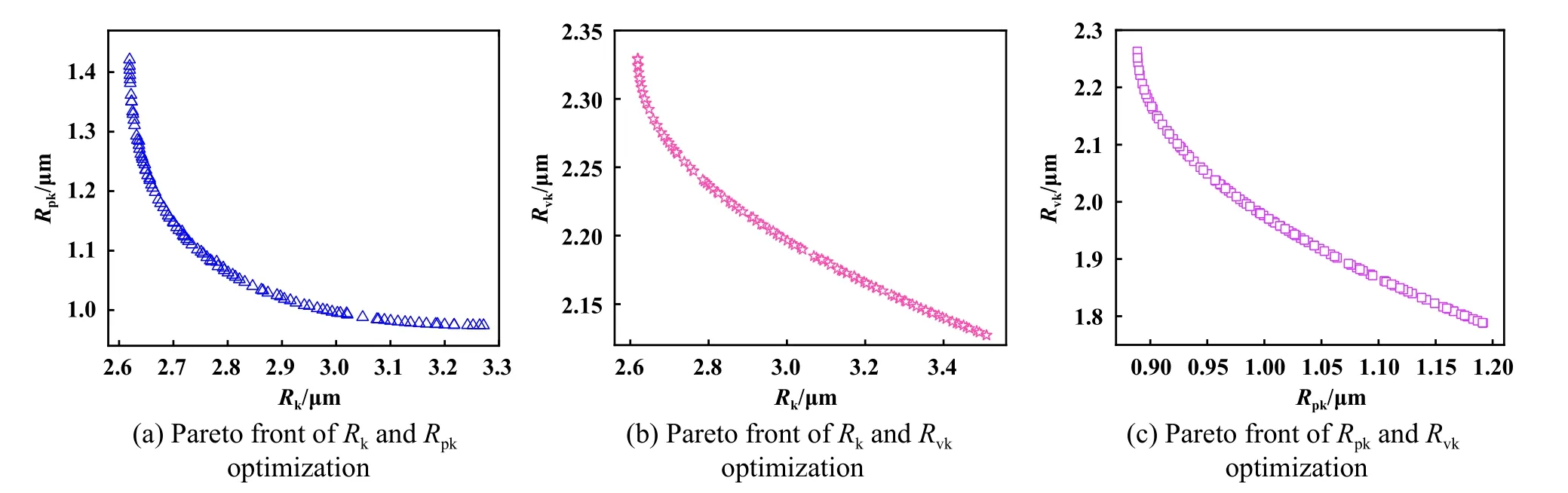
Fig.18 Pareto front of two objective optimization of roughness图18 粗糙度两目标优化结果的Pareto前沿

由图18(a)、(b)和(c)可知，Rk、Rpk和Rvk三者两两之间存在冲突关系，即其中1个量减小的同时，另外1个量增大，所以有必要求解粗糙度三目标优化的Pareto前沿.

4.2 缸套表面粗糙度三目标优化

三目标优化是使得3个粗糙度值同时达到相对最小，进而寻求珩磨压力P、珩磨头的往复速度VRe和珩磨头的旋转速度VR的最优参数组合.NSGA-Ⅱ算法里的初始种群数设为100，迭代次数为100次.

图19为Rk、Rpk和Rvk三目标优化结果的Pareto前沿图.此时根据实际加工需要，从候选的解集中选出最符合要求的解作为加工参数，即可获得最优的表面粗糙度.表10列出了Pareto前沿的优化结果中最优表面粗糙度值及其对应的加工参数.

Fig.19 Pareto front of optimization of Rk、Rpk and Rvk图19 Rk、Rpk和Rvk三目标优化结果的Pareto前沿

表10 最优表面粗糙度值及其对应的加工参数Table 10 The optimum surface roughness and the corresponding processing parameters

5 结论

本文中通过珩磨试验获得了不同加工参数下缸套表面Rk粗糙度参数集，运用广义回归神经网GRNN和RSM多元回归法构建缸套表面Rk粗糙度参数集的预测模型.结合三维响应曲面分析加工参数单个因素以及多个因素交互作用对表面粗糙度的影响.在此基础上，结合建立的粗糙度预测模型与NSGA-Ⅱ算法进行多目标优化，获得粗糙度多目标优化后的Pareto前沿.具体研究结论如下：

a.两种预测模型的决定系数都比较接近于1，说明两种预测模型的可信程度均比较高；与RSM预测模型相比，GRNN预测模型在预测Rk和Rpk时的精度更高，误差更小，R2分别提高了0.025和0.020，在预测Rvk时RSM模型预测精度更高，R2提高了0.057.

b.各因素对缸套表面粗糙度Rk的影响显著性的顺序依次为珩磨头旋转速度VR＞珩磨压力P＞珩磨头往复速度VRe；各因素对缸套表面粗糙度Rpk的影响显著性的顺序依次为珩磨压力P＞珩磨头旋转速度VR＞珩磨头往复速度VRe；各因素对缸套表面粗糙度Rvk的影响显著性的顺序依次为珩磨压力P＞珩磨头旋转速度VR＞珩磨头往复速度VRe.

c.Rk、Rpk和Rvk三者两两之间存在明显的相互冲突现象，其中1个量减小的同时，会有另外1个量增大，基于此借助多目标优化算法NSGA-Ⅱ获得了粗糙度多目标优化后Pareto最优解的Pareto前沿.