武昌区酸和溶解性固体湿沉降量主导因素分析

孙雪梅，陈睿弢，凌晓欢

(1.武汉环境投资开发集团有限公司，湖北 武汉 430020；2.湖北省生态环境厅武汉生态环境监测中心，湖北 武汉 430022)

1 引言

降水是常见的自然现象，同时也是大气污染物向水体和土壤迁移的重要途径。大气中各种污染物随降水沉降到地面的过程称为湿沉降，也称降水清除。湿沉降可分为酸沉降、溶解性固体沉降和不溶性颗粒物沉降。

由于人类活动对环境影响的加剧，导致降水水质恶化——主要是酸雨问题日益突出，对降水的监测成为环境质量监测工作的重要组成部分，围绕酸雨的各项理化特征也进行了大量的研究[1～10]。

很明显，某物质的湿沉降量=降水中某物质浓度×降水量。但实际降水过程中，浓度和降水量这两个直接影响因素对湿沉降量的影响力并不一定均等。这方面国内尚未见相关研究报道。

本文根据2014～2017年武汉市武昌区逐次降水监测数据，分析了该区域酸的湿沉降量(以H+计，以下简称酸沉降量)和溶解性固体的湿沉降量(以下简称TDS沉降量)各自的主导因素。

2 研究样本

2.1 降水采样与监测

依照关于大气降水采样、保存、分析的各项国家标准、行业标准[11～15]，设置固定采样点，对降水进行了持续采集和监测。采样点位、设备、频次、监测项目、分析方法详见表1。

2.2 数据选取

整体选取2014～2017年内所有逐次监测数据共计222组，作为本研究样本的数据源。

2.3 数据预处理

按公式(1)～(4)计算逐次降水的H+浓度、TDS浓度、酸沉降量、TDS沉降量：

H+浓度(mg/L)=10-pH×1000

(1)

酸沉降量(mg/m2)=H+浓度(mg/L)×降水量(mm)

(2)

TDS浓度(mg/L)=电导率(μS/cm)×0.5

(3)

TDS沉降量(mg/m2)=TDS浓度(mg/L)×降水量(mm)

(4)

3 统计分析方法

3.1 相关系数计算

相关系数一般是指简单相关系数，即Pearson相关系数，是度量2个变量之间线性相关程度的量，记为r。计算方法为：

(5)

由数学变换可知，除直接线性相关外，还有一些常见的相关关系可以很方便地转化为线性关系，同样可以用相关系数r来度量变量间的相关程度：

若Y与X呈对数相关，则Y与X的对数呈线性相关；若Y与X呈指数相关，则Y的对数与X呈线性相关；若Y与X呈幂相关，则Y的对数与X的对数呈线性相关。

本研究中，对于每组变量X、Y，均试算r(X,Y)、r(lnX,Y)、r(X,lnY)、r(lnX,lnY)4个相关系数，根据其绝对值大小判断该组变量最可能的相关关系，并相应地确定在后续回归分析中应采用的变量形式。

3.2 回归分析

根据3.1中确定的最可能相关关系，取合适的变量形式，构建一元线性回归模型，并估算模型参数，得到线性回归方程。通过函数形式变换，可将估算得到的线性回归方程转化为变量X、Y之间的函数关系式：Y=f(X)。

根据样本数据制成散点图，并绘制函数曲线Y=f(X)，形成回归分析图。从图上可直观检验回归曲线与观察值分布的相符性，或发现通过相关系数计算未能发现的其他相关关系。

回归方程参数的估算过程较为复杂，目前一般采用计算机软件辅助进行。

本研究中3.1相关系数计算和3.2回归分析的实际计算工作均使用Microsoft Excel 2010软件进行。

3.3 相关性的显著性检验

以上3.1和3.2的工作是基于一个假设，即变量X、Y相关。而这个相关性的存在是否可信，则需要运用假设检验的方法来判断。

本研究中p值的计算使用Microsoft Excel 2010，显著性水平限值按学术惯例取0.01。

4 结果与分析

4.1 酸沉降量的主导因素

4.1.1 酸沉降量与H+浓度的相关性

根据逐次降水的H+浓度、酸沉降量，制成酸沉降量与H+浓度变化图(图1)。

图1 酸沉降量与H+浓度变化

由图1可见，酸沉降量与H+浓度的变化曲线峰谷位置较一致，吻合程度较高。

进一步采用统计方法，计算酸沉降量与H+浓度的相关系数，并作显著性检验和回归分析。结果如图2。

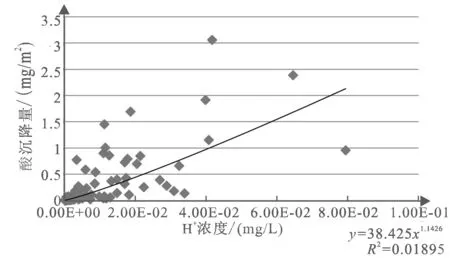
图2 酸沉降量与H+浓度相关性

分析结果显示，酸沉降量与H+浓度相关性极其显著(p≈0)，二者呈幂函数关系，相关系数r=0.9052。

4.1.2 酸沉降量与降水量的相关性

根据逐次降水的降水量、酸沉降量，制成酸沉降量与降水量变化图(图3)。

图3 酸沉降量与降水量变化

由图3可见，酸沉降量与降水量的变化曲线峰谷位置仅有部分一致，降水量波动明显更加频繁。

进一步采用统计方法，计算酸沉降量与降水量的相关系数，并作显著性检验和回归分析。结果如图4所示。

图4 酸沉降量与降水量相关性

分析结果显示，酸沉降量与降水量相关性也极其显著(p≈0)，二者也呈幂函数关系，相关系数r=0.6432。

4.1.3 小结

酸沉降量与H+浓度的变化曲线峰谷位置较一致，酸沉降量与降水量的变化曲线峰谷位置仅有部分一致，降水量波动明显更加频繁。

酸沉降量与H+浓度和降水量均有极显著相关性，呈幂函数关系。酸沉降量与H+浓度相关系数高达0.9052，相关性极强；酸沉降量与降水量相关系数为0.6432，相关性相对较弱。

相关研究表明，降水H+浓度与降水量之间存在显著的中等正相关[6]，因此推断，酸沉降量与降水量的相关性很大程度上是受酸沉降量与H+浓度相关性的间接影响，酸沉降量主要取决于H+浓度，降水量是次要因素。

4.2 TDS沉降量的主要影响因素

4.2.1 TDS沉降量与TDS浓度的相关性

根据逐次降水的TDS浓度、TDS沉降量，制成TDS沉降量与TDS浓度变化图(图5)：

图5 TDS沉降量与TDS浓度变化

由图1可见，TDS沉降量与TDS浓度的变化曲线峰谷位置无明显关联。

进一步采用统计方法，计算TDS沉降量与TDS浓度的相关系数，并作显著性检验和回归分析。结果如图6所示。

图6 TDS沉降量与TDS浓度相关性

分析结果显示，TDS沉降量与TDS浓度相关性显著(p<0.005)，二者呈幂函数关系，相关系数r=0.2022。

4.2.2 TDS沉降量与降水量的相关性

根据逐次降水的降水量、TDS沉降量，制成TDS沉降量与降水量变化图(图7)。

图7 TDS沉降量与降水量变化

由图3可见，TDS沉降量与降水量的变化曲线峰谷位置有部分一致。

进一步采用统计方法，计算TDS沉降量与降水量的相关系数，并作显著性检验和回归分析。结果如图8所示。

图8 TDS沉降量与降水量相关性

分析结果显示，TDS沉降量与降水量相关性极其显著(p≈0)，二者也呈幂函数关系，相关系数r=0.6816。

4.2.3 小结

TDS沉降量与TDS浓度的变化曲线峰谷位置无明显关联，TDS沉降量与降水量的变化曲线峰谷位置有部分一致。

TDS沉降量与TDS浓度和降水量均显著相关，呈幂函数关系。TDS沉降量与TDS浓度相关系数仅0.2022，相关性较弱；TDS沉降量与降水量相关系数为0.6816，相关性强。

相关研究表明，降水电导率与降水量之间存在显著的强负相关[16]，所以TDS浓度和降水量对TDS沉降量的影响是相互拮抗的，TDS浓度和降水量对TDS沉降量均有影响，但降水量是主导因素。

5 结论

(1)H+浓度和降水量对酸沉降量都有明显影响，H+浓度是主导因素，降水量是次要因素。

(2)降水量是TDS沉降量的主导因素。TDS浓度对TDS沉降量也有影响，但影响程度很小。

(3)较大的降水量能明显清除更多大气污染物，改善环境空气质量，但同时在一定程度上会增加酸沉降，不利于地表生态环境。

(4)减少酸雨，提高降水pH值(即减小降水H+浓度)能有效降低降水量增大带来的酸沉降增加风险。