阻尼累加离散灰色预测的Smith预估智能灌溉系统*
2022-08-12谢佩军张育斌
谢佩军, 张育斌
(1. 浙江纺织服装职业技术学院机电与轨道交通学院,浙江宁波,315211; 2. 西安交通大学,西安交通大学机械制造系统工程国家重点实验室,西安市,710054)
0 引言
我国是传统农业大国,农业用水量约占总用水量70%左右,但传统灌溉技术的有效利用率低、水肥浪费严重。随着物联网、大数据、人工智能等技术不断应用于农业工程领域,促进智慧农业的快速发展,国家高度重视智慧农业的发展问题[1-2]。智慧农业系统性地将智能技术、传感技术等融入农业全产业链,实现智能化决策、精准化控制,有效提高水肥利用率和改善农业生态环境。智能灌溉系统是智慧农业的核心系统,灌溉控制策略是灌溉系统的关键技术,决定了灌溉系统的智能化、精准化程度[3-4]。智能灌溉系统是时滞性、非线性、多随机干扰的复杂系统,经典PID控制结构简单、参数易整定[5-6],但存在参数变化鲁棒性差、抗干扰能力不强等缺点,控制精度难以满足智能灌溉的控制要求,学者们不断提出改进算法优化模型。朱德兰[7]、刘洪静[8]等将模糊PID应用于灌溉控制,较好地解决了系统的非线性但控制误差不稳定。王正等[9]提出了变论域模糊PID控制的智能滴灌系统实现自适应调节控制参数,均能不同程度改善灌溉控制精度和系统稳定性。刘斌等[10]设计了Smith预估结合模糊控制的灌溉决策系统,采用Smith预估补偿器消除系统时滞性。智能灌溉系统的控制对象易受到气候、土壤等诸多不确定因素的影响,GM及其改进模型被广泛应用于工业、农业、旅游业等领域不确定性系统的规律预测[11-13]。谢乃明等[14]基于差分方程提出DGM避免了从离散模型参数到连续模拟预测的转换误差。Beníte等[15]利用阻尼趋势参数优化GM模型的预测数据变化趋势。Liu等[16]提出DAGM能够适应性调整预测序列趋势,有效提升了模型拟合效果和预测精度。
灌溉系统具有非线性、多干扰和时滞性等特点,控制对象惯性大、影响因素多,为了实现灌溉控制的智能决策与精准灌溉,本研究融合灰色预测和模糊PID控制模型。采用模糊控制解决模型不精确问题,设计函数型伸缩因子自适应调整模糊控制变量论域,采用Smith预估补偿器消除灌溉系统的时滞性影响。结合DGM模型和DAGM模型的超前控制与变化趋势预测优势,提出DADGM克服从离散方程到微分方程的转换误差以提高预测精度。最后,利用仿真实验模拟与实际灌溉测试分析,对所构建控制模型进行有效性验证。
1 智能灌溉系统构成
智能灌溉系统包括水肥气供给模块、数据采集模块和灌溉控制模块,系统工作原理如图1所示。水肥气供给模块由蓄水池、恒压供水系统、增氧罐、母液罐、文丘里管等构成,为灌溉系统提供水肥和氧气;数据采集模块由流量计、氧传感器、EC传感器、pH传感器、压力表等构成,实时监测灌溉状况、动态采集灌溉数据;灌溉控制模块由变频控制系统、变频吸肥泵、增氧泵、离心变频泵、气液混合泵、电磁阀等构成,根据灌溉设定值和实时灌溉数据实现水肥气流动状态的智能控制。
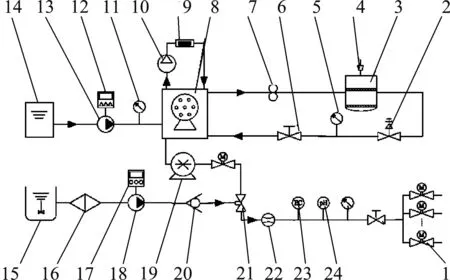
图1 水肥气灌溉原理图Fig. 1 Schematic diagram of oxyfertigation system1.电磁阀 2.安全阀 3.气液分离罐 4.排气阀 5.压力表 6.手动阀 7.气液混合泵 8.增氧罐 9.氧传感器 10.真空泵 11.压力表 12.恒压供水系统 13.离心变频泵 14.蓄水池 15.母液罐 16.过滤器 17.变频控制系统 18.变频吸肥泵 19.增氧泵 20.单向阀 21.文丘里管 22.流量计 23.EC传感器 24.pH传感器
2 灌溉系统控制策略
智能灌溉系统以EC/pH传感器反馈信号为灌溉控制主要依据,建立可靠的EC/pH数学模型是智能决策和精准灌溉的基础。肥液电导率EC值和酸碱度pH值是灌溉系统肥液的重要监测指标[17-18],系统收到EC/pH反馈信号结合作物需水量,通过变频器、泵、电磁阀等执行机构实现灌溉控制,属于典型一阶纯滞后系统。研究发现EC值与灌溉肥液浓度存在线性相关性,测量EC值可以间接监测灌溉肥液的肥素浓度,EC值能够用于表征灌溉肥液的浓度值。酸碱度pH值也是灌溉过程肥液变化的重要监测指标,灌溉系统通常专设pH值调节管道,通过调节灌溉肥液的pH值来改良土壤环境。
EC传感器的传递函数为
(1)
pH传感器的传递函数为
(2)
式中:X(s)——肥液浓度函数;
σ(s)——肥液EC值函数;
H(s)——肥液pH值函数。
灌溉系统在灌溉管道的毛管处实时监测灌溉肥液浓度,根据EC/pH传感器响应时间变化,结合EC值和pH值控制策略,检测灌溉过程各时间段肥液浓度值,通过灌溉数据分析、变化趋势预测和系统决策实现智能灌溉和精准灌溉。
3 基于Smith预估变论域模糊PID控制
3.1 模糊PID控制
经典PID控制结构简单、模型易构建、参数易整定,广泛应用于工业领域的控制系统。对于时变性、非线性的智能灌溉系统,PID控制的参数整定复杂度将大幅增加,且控制精度难以满足要求。模糊控制无需建立精确的数学模型,具有较强的鲁棒性,能够有效改善控制系统的非线性和时变性。模糊PID灌溉控制以智能灌溉系统的决策量r(t)与实际量u(t)的偏差e(t)和偏差变化率ec(t)作为输入量,经模糊化、模糊推理和模糊决策输出参数修正量ΔKP、ΔKI、ΔKD,实时修正控制参数提高系统响应性能,如图2所示。
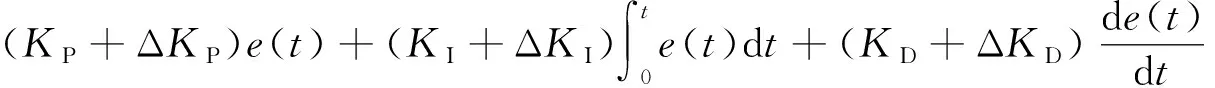
(3)
式中:KP——比例系数;
KI——积分系数;
KD——微分系数。

图2 模糊PID灌溉控制结构图Fig. 2 Fuzzy PID control structure
根据智能灌溉系统的灌溉控制要求,e(t)和ec(t)的语言变量模糊子集均取为{负大NB,负中NM,负小NS,零ZO,正小PS,正中PM,正大PB},模糊论域均取为{-3,-2,-1,0,1,2,3}。综合考虑稳定性、计算量、灵敏度等[19],模糊输入隶属度函数选用TRIMF型隶属度函数,结合灌溉系统控制变量的变化规律、稳定性、超调量等因素,通过分析和仿真制定参数修正量的模糊规则如表1所示。

表1 模糊控制规则表Tab. 1 Fuzzy control rules
3.2 变论域模糊PID控制
论域范围和模糊等级划分决定了模糊PID控制器的控制精度,为了提高模糊控制适应性和参数调节精度,引入变论域思想构建变论域模糊PID控制器,能够在模糊等级不变的情况下,通过伸缩因子自适应调整变量论域[20]。智能灌溉系统具有非线性、大惯性等不确定性特点,在实际控制时难以建立所有伸缩因子的控制规则。函数模型的伸缩因子选用某些特殊函数,能够改善因缺少模糊规则导致控制性能不稳定问题。本文结合文献分析和实验仿真[21-22],选用指数函数模型设计变论域伸缩因子
(4)
式中:α(e)——e(t)的伸缩因子;
α(ec)——ec(t)的伸缩因子;
β[e(t),ec(t)]——参数修正量共同伸缩因子;
E1、E2——初始论域边界;
θ——充分小的常量;
ρi——因子参数,ρi∈[0,1]。
设计参数ρi无实际物理意义,目前没有通用的参数整定方法,一般以实际应用场合情况和具体应用要求为依据进行设定。综合考虑灌溉系统的水肥气控制实际需求、系统决策量r(t)与实际量u(t)的偏差e(t)和偏差变化率ec(t)的控制性能要求和伸缩因子设计原则,经过反复灌溉系统实验和参数调试对比分析,实时修整因子设计参数
(5)
式中:υ——充分小正数,υ∈(0,1)。
确保系统变量的协调性,令ρi(i=1,2,3,4)均相等。代入式(4)可以得到新型伸缩因子
(6)
稳定有效的伸缩因子应具备对偶性、避零性、单调性、协调性等基本性能,从而确保灌溉控制系统能够迅速调整e(t)和ec(t),下面以正规性和避零性为例对本文提出新型函数型伸缩因子进行性能验证。
1) 避零性。由于ρi∈[0,1],令e(t)→0时则有
(7)
满足避零性原则确保伸缩因子不为0,从而避免隶属度函数收缩至“零点”。
2) 正规性。当e(t)取论域边界值,即e(t)=±E1,ρ1=1时有
(8)
(9)
α[e(t)]满足正规性原则,确保变论域模糊控制器初始采样偏差有实际意义。
同理可以验证变量α[e(t)]和α[ec(t)]的对偶性、避零性、单调性、协调性、正规性等性能,容易验证其线性组合β[e(t),ec(t)]满足稳定性原则。因此,所设计的函数型伸缩因子具备基本性能,可用于构建变论域模糊控制器。
3.3 基于Smith预估的变论域模糊PID控制
智能灌溉系统受天气、土壤、需水量等因素的动态影响大,是强耦合、多干扰、大时滞的非线性系统,容易出现不稳定状态。考虑到灌溉过程大惯性、大时滞导致系统控制易产生超调或振荡,变论域模糊PID控制引入Smith预估补偿,对灌溉系统存在的延时滞后进行补偿以改善迟延引起的大超调量,提升灌溉系统的控制精度和稳定性。
Smith预估控制结构简单、适用性好,通过预估补偿将系统纯滞后环节移出闭环回路,从而得到无迟延的反馈信号,能够有效改善系统时滞性[23-24]。基于Smith预估的变论域模糊PID控制以智能灌溉系统的决策量r(t)与实际量u(t)的e(t)和ec(t)作为输入量,由伸缩因子自适应调整变量论域,通过模糊化、模糊推理、模糊决策得到修正量ΔKP、ΔKI、ΔKD实时修正参数。利用Smith预估补偿环节对灌溉控制系统的滞后时间进行补偿,确保延时数据信息能够及时送达执行系统,控制执行机构实现灌溉肥液EC值、pH值的动态调节,优化系统控制效率和控制性能,系统控制结构如图3所示。

图3 Smith预估变论域模糊PID控制结构图Fig. 3 Smith predictive variable universe FPID control structure
4 阻尼累加离散灰色预测的Smith预估灌溉控制
灰色预测是灰色系统理论的重要预测模型[25],能够对含有不确定因素的系统进行预测,灰色预测模型GM(1,1)自提出以来扩展出多种新模型,被广泛应用于航空航天、工业生产、农业灌溉等领域[26-27]。针对GM(1,1)模型预测数据变化过快,导致系统预测效果不理想的问题,Benítez[15]、Liu[16]等提出DAGM,利用阻尼趋势参数减缓预测过程数据变化趋势,提高了数据拟合和预测精度。智能灌溉系统是非线性、多因素的典型灰色系统,受天气、土壤、作物状况等可测、未知或未确定等因素影响,DAGM适用于灌溉系统的控制预测与决策。但灌溉控制模型参数估计采用离散形式,而模拟预测采用连续形式,存在从离散方程到微分方程的转换误差,势必影响实际灌溉控制精度。本文结合离散GM模型和DAGM模型的性能优势,提出阻尼累加离散GM模型(DADGM)。
4.1 阻尼累加离散GM模型(DADGM)
实际灌溉过程中肥液经由管道输送存在延时,灌溉模型训练的初始数据不变将会影响系统预测结果,因此选用序列初始点的迭代初值作为迭代基准构建预测模型。
设X(0)为原始数据序列
X(0)=(x(0)(1),x(0)(2),…,x(n)(n))
(10)
一次累加生成序列为
X(1)=(x(1)(1),x(1)(2),…,x(1)(n))
(11)
设定阻尼参数τ∈(0,1],则τ阶阻尼累加生成序列为
X(τ)=(x(τ)(1),x(τ)(2),…,x(τ)(n))
(12)

(13)
X(τ)紧邻均值序列
T(τ)=(t(τ)(1),t(τ)(2),…,t(τ)(n))
(14)
其中t(τ)(k+1)=[x(τ)(k+1)+x(τ)(k)]/2
(15)
则得到阻尼累加GM模型(DAGM)
x(τ)(k+1)-x(τ)(k)+at(τ)(k+1)=b
(16)
可以由式(16)通过最小二乘法得到模型发展系数a和灰作用量b,但DAGM模型存在从离散方程到微分方程产生的转换误差问题。
根据原始序列X(0)和τ阶阻尼累加生成序列,可得阻尼累加离散GM模型(DADGM)为
x(τ)(k+1)=β1x(τ)(k)+β2
(17)
参数β1、β2可通过最小二乘法求得
[β1,β2]T=(BTB)-1BTY
(18)
其中
(19)
通过递推可得时间响应函数
(20)
则τ阶阻尼累加离散生成序列为

k=1,2,…,n
(21)
4.2 基于DADGM的Smith预估智能灌溉控制
根据PID控制和模糊控制的模型性能特点,设计新型函数型伸缩因子自适应调整模糊控制变量论域,采用Smith预估补偿灌溉系统的时滞性,构建Smith预估补偿的变论域模糊PID控制器。结合DGM模型和DAGM模型的超前控制与数据预测性能优势,提出基于DADGM的Smith预估变论域模糊PID控制器,融合超前控制的灰色预测模型,实现水肥气灌溉系统的智能决策与精准灌溉,系统控制结构如图4所示。

图4 基于DADGM的Smith预估智能灌溉控制结构图Fig. 4 Smith predictive intelligent irrigation system based on DADGM
智能灌溉系统以EC/pH传感器反馈信号依据,由DADGM模块预测作物所需水肥气量,给出灌溉预测值;通过水肥气智能决策值匹配相应灌溉水量的施肥量和增氧量,确定水肥气信号;再根据该预测信号进行Smith预估变论域模糊推理得到系统参数;最后经由控制器确定肥气量输出信号,实现变频吸肥泵、增氧泵、电磁阀等执行机构的智能灌溉控制。
5 仿真试验与灌溉测试
5.1 仿真试验对比分析
为了分析所设计模型的性能指标和控制效果,采用Matlab/Simulink环境进行建模仿真,建立FPID(模糊PID)、NVUFP(新型变论域模糊PID)、DGM-NVUFP(基于离散灰色预测的新型变论域模糊PID)和DADGM-SVUFP(基于阻尼累加离散灰色预测的Smith预估变论域模糊PID)四个模型进行控制性能对比研究。结合临界比例法[28]和仿真试验综合分析整定各PID模型的初始参数均为KP0=11.86、KI0=0.52、KD0=0.08,经灌溉数据试验调试设定NVUFP、DGM-NVUFP和DADGM-SVUFP三个模型的变论域伸缩因子设计参数ρ1=ρ3=0.85、ρ2=ρ4=0.25,设定DADGM-SVUFP模型的最优阻尼累加参数τ=0.921 8。通过实施4个控制模型的水肥灌溉控制模拟仿真试验,得到肥液流量控制仿真曲线如图5所示,进而对比分析模型阶跃响应曲线及性能参数如表2所示。

图5 灌溉控制仿真曲线图Fig. 5 Simulation curve of irrigation control

表2 控制模型性能参数Tab. 2 Control model performance parameters
根据灌溉控制仿真曲线对比分析模型性能,NVUFP的上升时间和调节时间都少于FPID,且超调量为9.2%比FPID减少了10.3%,基于新型函数型伸缩因子的变论域有效提升了系统自适应能力和响应速度。DGM-NVUFP的上升时间为3.21 s,调节时间为8.12 s,均少于FPID和NVUFP,其超调量为5.4%,相比FPID和NVUFP分别减少了14.1%和3.8%,说明离散灰色预测进一步改善了模型控制效果。FPID、NVUFP和DGM-NVUFP均存在一定的震荡和稳态误差,融合DADGM和Smith预估补偿的DADGM-SVUFP的超调量和稳态误差均为零,响应曲线平稳无震荡且调节时间最小,说明模型动态性能、控制精度和稳定性均得到优化。
5.2 实际灌溉测试
控制模型的实际灌溉测试在宁波市农业科学研究院农业技术实验园进行现场试验,为了保证灌溉测试结果的有效性,在灌溉环境保持一致的条件下,将基于FPID、NVUFP、DGM-NVUFP和DADGM-SVUFP控制模型的智能灌溉设备实施灌溉流量分组测试。灌溉系统主管由变频恒压系统提供0.4 MPa水压,采用斯美特EMF5000流量计在线监测灌溉肥液流量,EC传感器和pH传感器实时监测肥液EC值和pH值。考虑到灌溉肥液在管道中流动延时,流量计监测数据存在短暂时间滞后,灌溉初始2 s均未检测流量。经过现场多次测试数据比较分析,选取0.5 s采样周期符合灌溉实际情况,每组进行3次测试取平均值作为灌溉测试数据,如表3所示。
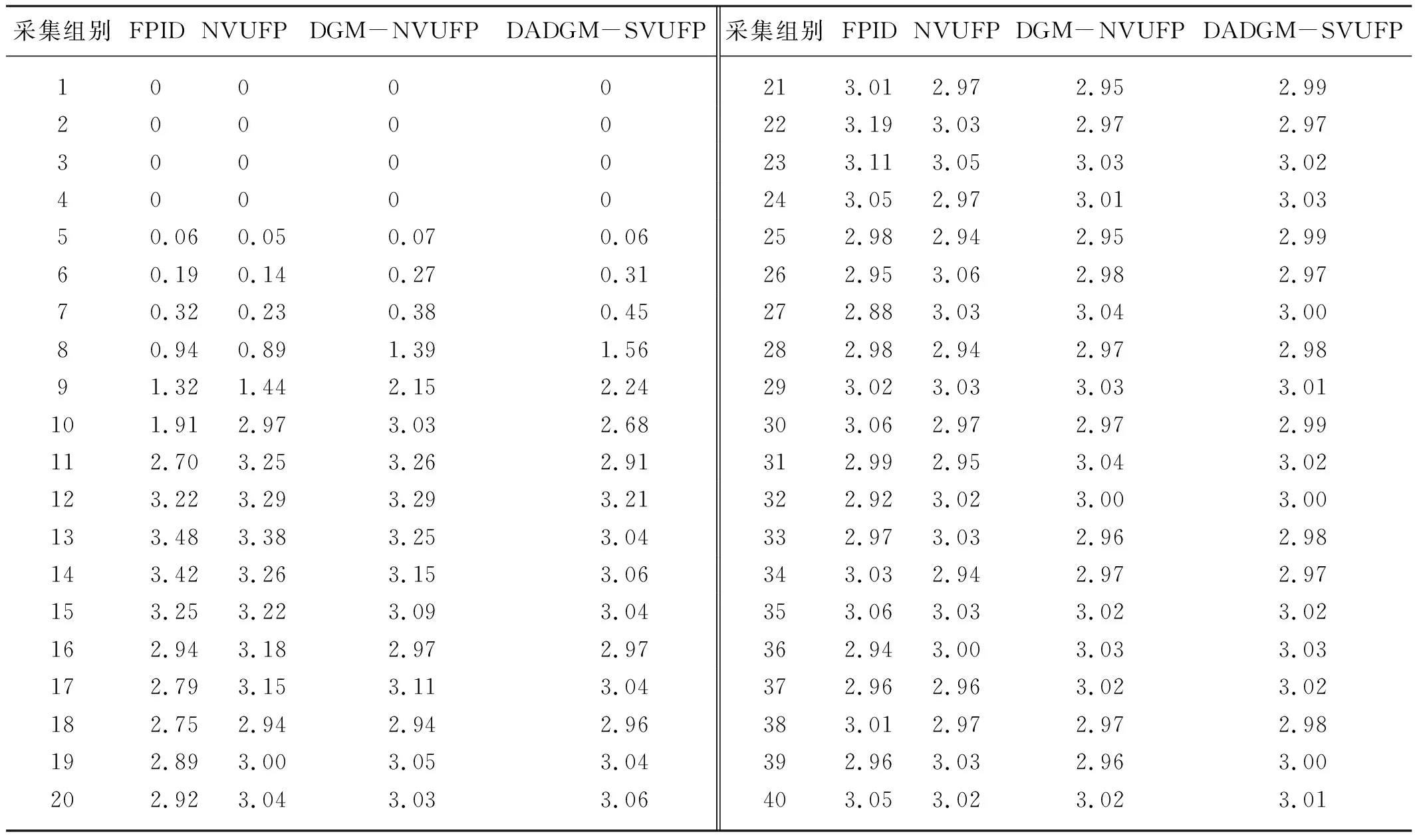
表3 灌溉测试数据Tab. 3 Irrigation test data L/min
根据表3灌溉测试数据分析可得,FPID和NVUFP模型灌溉控制系统实际灌溉流量均需要12 s以上才能达到稳态值3±0.6 L/min,DGM-NVUFP模型控制系统10 s左右能达到3±0.6 L/min,DADGM-SVUFP模型灌溉控制系统的实际灌溉测试数据最快达到稳定状态,7 s左右达到稳态流量3±0.6 L/min,10 s左右能够达到最终稳态3±0.3 L/min,而其他模型均存在震荡现象难以达到3±0.3 L/min,说明DADGM-SVUFP模型实际灌溉的稳态误差最小、系统稳定无震荡,控制性能优于其他模型。实际灌溉测试数据验证DADGM-SVUFP模型的响应速度、鲁棒性和控制精度均能够满足智能灌溉系统实际要求。
6 结论
1) 设计的智能灌溉系统包括水肥气供给模块、数据采集模块和灌溉控制模块,建立EC/pH传感器模型,系统以EC/pH传感器反馈信号为灌溉控制主要依据,研究了灌溉系统控制策略为智能灌溉奠定基础。
2) 针对模糊PID控制器应用于智能灌溉存在控制精度不高、适应性不强等问题,引入变论域思想设计了指数函数型伸缩因子自适应调整模糊变量论域,采用Smith预估补偿器消除系统时滞性影响,改善了系统适应性和动态响应性能。融合具有超前预测能力的DGM和DAGM模型性能优势,提出了DADGM提前预测肥液调节量变化趋势,有效提升灌溉系统的稳定性和控制精度。
3) 建立FPID、NVUFP、DGM-NVUFP和DADGM-SVUFP四个模型进行控制性能对比试验和灌溉测试。实验结果表明,DADGM-SVUFP的调节时间最小为6.83 s,远小于其他模型;FPID、NVUFP和DGM-NVUFP均存在一定的震荡和稳态误差,DADGM-SVUFP的超调量和稳态误差均为零,响应曲线平稳无震荡;灌溉测试进一步验证DADGM-SVUFP模型在实际灌溉条件下具备动态响应性好、控制精度高、鲁棒性好等优势。因此,基于阻尼累加离散灰色预测的的Smith预估变论域模糊PID模型,具有符合智能水肥气灌溉系统要求的控制精度和动态性能,为智慧农业发展提供有力的技术支持。
