台架负载模拟控制方法研究*

韦宇豪，李忠利, 2，杨永军，杨淑君

(1. 河南科技大学车辆与交通工程学院，河南洛阳，471003； 2. 河南省汽车节能与新能源重点实验室，河南洛阳，471003)

0 引言

动力台架试验是车辆动态性能研究的一个重要途径[1-6]。除了需要满足动力系统需求外，还需要能够模拟整车在动态条件下的负载，普通静态模拟已无法满足测试系统的需要。随着电力电子、电机控制技术的发展，不少学者逐步采用电机控制负载模拟[7-10]的方法来进行动态加载。周志立等[11]通过分析电模拟理论基础，推到电模拟时所需的补偿力矩，根据luenberger理论，建立角加速度观测器来获取角加速度信号，最后控制电机来实现底盘测功机电惯量模拟。通过多次滑行和加速性能试验使得测试精度相较原有机械方案提高4.4%。李文礼等[12-13]建立车辆动力学模型并加入台架系统转动部件惯量参数识别。通过分析负载模拟原理，设计出基于转速自适应动态预测控制的负载模拟方法，使得转速预估更加精准。最后在动力总成动态模拟控制中利用该方法实现了较快的响应速度，达到了动态模拟实车工况的目的。马瑞海等[14]在防抱死制动试验台上设计随机网络诱导延时补偿负载模拟算法，通过系统增广将随机系统跟踪控制问题转化为鲁棒镇定问题并分析系统性能，接着通过非线性优化问题得到系统控制增益，从而实现用电惯量对机械转动惯量的模拟。最后进行了防抱死制定测试，结果表明补偿算法可大幅度提高负载模拟精度。现有文献对负载模拟虽有一定的研究成果，但实际道路情况往往复杂多变，而角加速度可以实时反映实际驱动系统转矩和负载转矩在台架上的动态变化，故仍需要采取措施对角加速度进行精确处理，增强台架负载跟踪性能。

本文以原PS结构混合动力汽车为基础，首先在Matlab/Simulink中建立车辆动力学、加载电机等相关模型；其次设计了逆模型负载模拟控制方案并设计了相应的控制器模型，在不同采样频率和测频精度下经PI自适应卡尔曼滤波算法实时计算角加速度和负载扭矩；最后经逆模型控制进行仿真模拟测试，实现了动态加载功能，为硬件在环测试提供参考。

1 系统结构

混合动力台架方案如图1所示，其中：1、10为离合器；2、4、7、9、11、13、16、18为轴承座；3、8、12、17为同步带轮；5、15为同步带；6、14、19、20为弹性联轴器。发动机经离合器1、同步带与电机1相连；电机1经同步带、离合器10与电机2相连；负载电机经传感器通过同步带与电机2相连。该方案结构分动力系统和加载系统两大部分。动力部分由发动机、两个电机、两个离合器组成；加载部分由联轴器、扭矩传感器、负载电机组成。

加载部分和待测动力系统的结合点即是模拟点；按照动力切换模式不同，各种模拟点分别对应不同的待考察部件。如：发动机单独驱动、单电机驱动或双电机驱动等，则负载电机的模拟点可以在离合器前端、离合器后端、电机后端等。

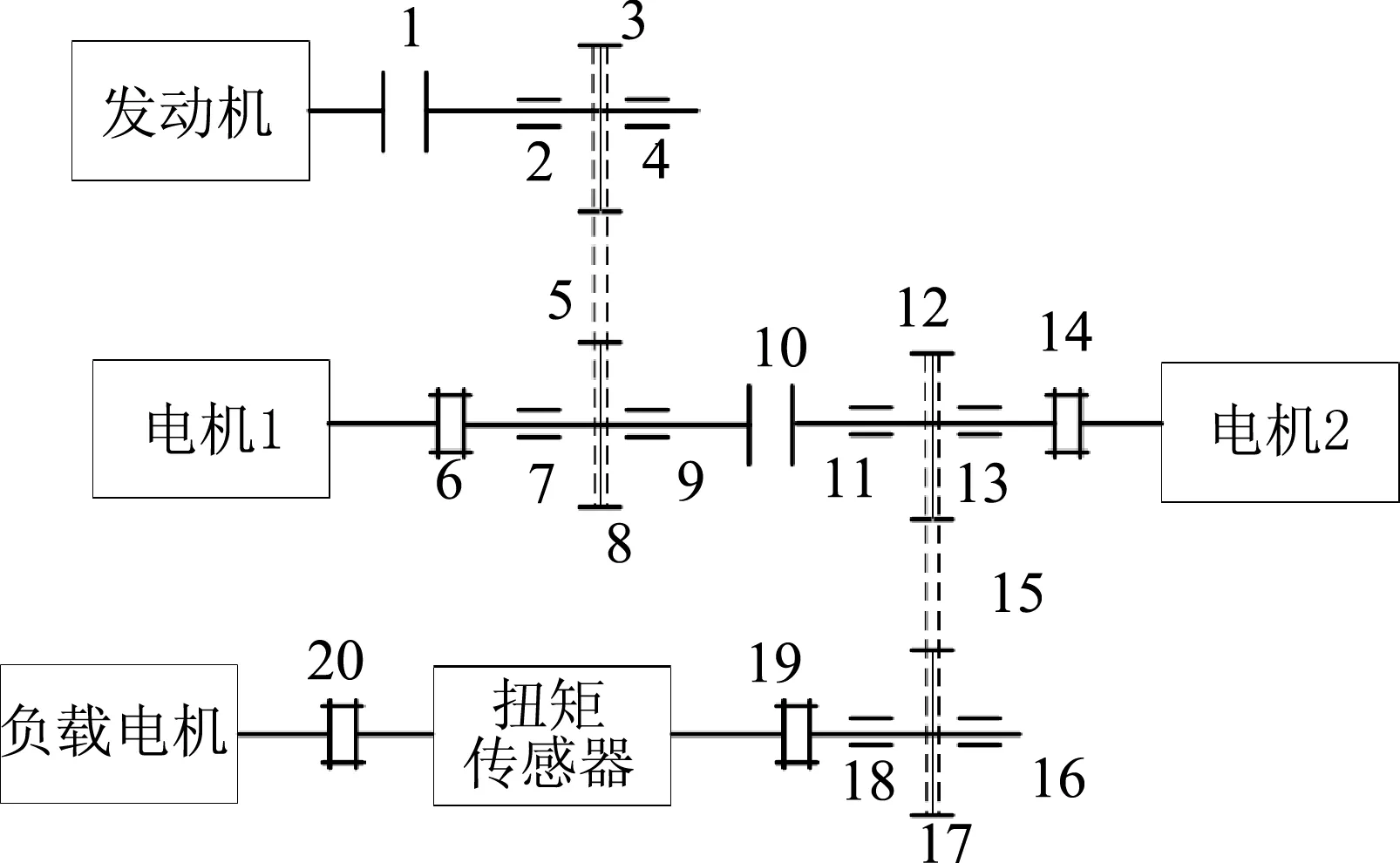
图1 台架方案设计布置Fig. 1 Design and layout of the platform scheme

2 系统模型建立

2.1 负载电机模型

负载电机采用高效率三相交流伺服异步电机，忽略铁损并假设三相绕组产生的磁动势按正弦分布。

d-q坐标系下电压方程

(1)

式中：usd、Usq——两相定子绕组电压；

urd、urq——两相转子电压；

isd、isq——两相等效定子电流；

ird、irq——两相等效转子电流；

ψsd、ψsq——两相定子磁链；

ψrd、ψrq——两相转子磁链；

Rs——定子绕组阻值；

Rr——转子绕组阻值；

p——微分算子；

Ls——定子两相等效自感；

Lr——转子两相等效自感；

Lm——定转子两相等效互感；

θ——旋转坐标系与静止坐标系之间夹角；

θr——转子转过角度。

坐标系旋转速度为ωdq，令pθ=ωdq，异步电机转子转速ωr，则有电压方程如式(2)所示。

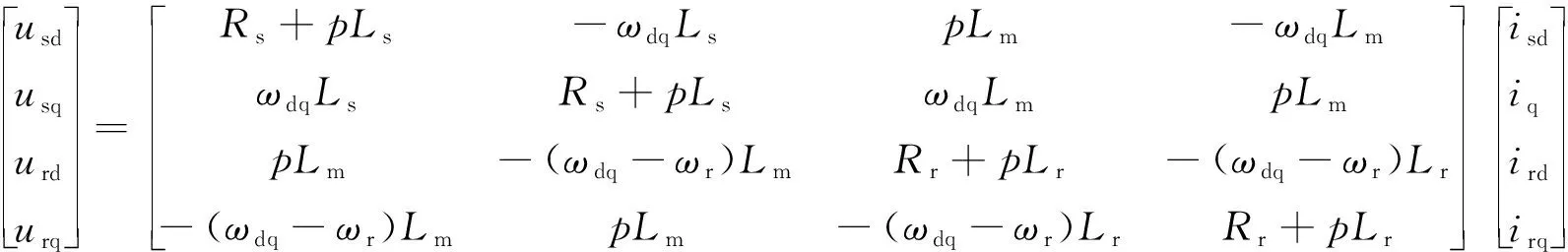
(2)

磁链方程

(3)

转矩方程

Te=npLm(isqird-irqisd)

(4)

运动方程

(5)

令d-q坐标系下旋转速度ωdq等于电源角速度ω1，则变换成同步旋转坐标系M-T。转差角速度ωs=ω1-ωr。异步电机转子磁场定向控制的矢量控制方程

(6)

式中：Tr——转子励磁时间常数；

ism——定子电流励磁分量；

ist——定子电流转矩分量；

ωr——转子旋转角速度；

CIM——转矩系数。

2.2 动力学模型

根据动力学原理可知，汽车在行驶过程中受到阻力可由非惯性力Fa及惯性力Fj两大部分表示。非惯性力Fa包含Ff滚动阻力，Fi坡度阻力，Fw空气阻力。

(7)

(8)

F=Fa+Fj

(9)

式中：m——汽车质量；

g——重力加速度；

f——滚动阻力系数；

α——坡度角；

CD——空气阻力系数；

A——迎风面积；

υ——车速；

δ——换算系数；

F——总力矩。

将车速转化为轴转速，则非惯性阻力折算到电机输出端的扭矩

(10)

(11)

式中：Ta——阻力折算到输出轴端的非惯性阻扭矩；

r——车轮半径；

ω——轴转速；

γ——蠕化率；

η——传动效率；

i——总传动比。

由动能相等原则可知汽车平动惯量与轴转动惯量可相互转化。因此在台架上模拟整车惯性力矩时引入等效惯量Je。

(12)

式中：m′——平移质量。

根据上述等效惯量推导，则有动力端输出扭矩方程，如式(13)所示，等式右端则是模拟目标的惯性力矩。

(13)

式中：Tm——动力系统端的输出扭矩(与被测模拟点位置有关)。

2.3 台架系统模型

根据图1中系统结构，负载模拟部分由负载电机、联轴器、扭矩传感器等组成。根据动力系统控制策略不同，选择发动机或驱动电机1、2带动负载电机运动，忽略编码器惯量等因素的影响，台架系统由式(14)得到。

(14)

式中：T1——被测模拟点端的输出扭矩；

Td——负载电机的输出扭矩；

B——台架阻尼系数；

Jt——台架上所有转动部件的惯量之和，由联轴器、负载电机和驱动电机等的转动惯量组成。

试验台控制部件不同、待测模拟点不同等，都会影响台架惯量值Jt大小，其大小影响加载扭矩差值。

3 负载模拟控制方法

3.1 逆模型控制

根据上述模型分析设计了基于机械负载的逆动力学模型控制，即根据输出轴端角加速度求得负载电机额外的补偿扭矩，这种方式实质是通过对负载电机的转矩控制[15-18]实现车辆负载的模拟。忽略弹性联轴器及传动轴变形后经拉普拉斯变换后得到，如式(15)所示。

(15)

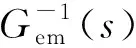
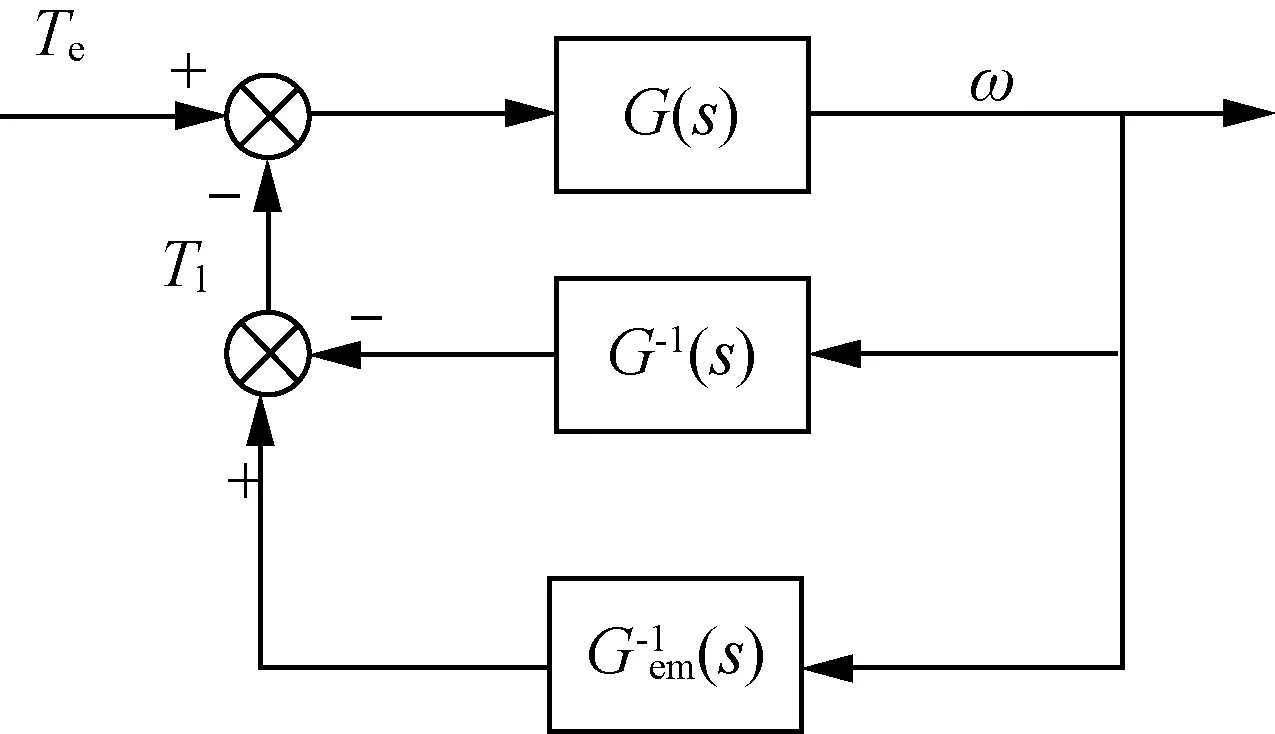
图2 逆模型控制原理图Fig. 2 Inverse model control principle diagram

3.2 控制器模型设计

电机内部动态设计如图3所示。

图3 电机动态结构Fig. 3 Motor dynamic structure

根据图3结构，设被模拟转动惯量J1可以表示为

(16)

在外力作用下由转速ω生成指令电流I的控制器，其传递函数G(s)

(17)

对比分析得到

(18)

J1=J+JN

(19)

式中：JN——新产生的惯量；

J——物理惯量；

K——转矩系数。

实际工程中用惯性环节代替纯微分环节则有

(20)

式中：τn——时间常数。

根据式(16)～式(20)可得到电流控制结构，如图4所示。

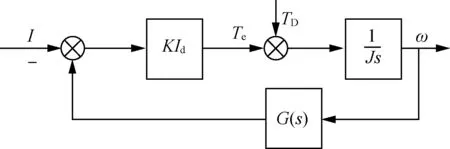
图4 电流控制结构Fig. 4 Current inertia control structure

采用电流控制时因没有实际扭矩反馈对负载模拟有一定影响，所以在此基础上增加扭矩闭环控制，模拟转动惯量Jf动态结构如图5所示。

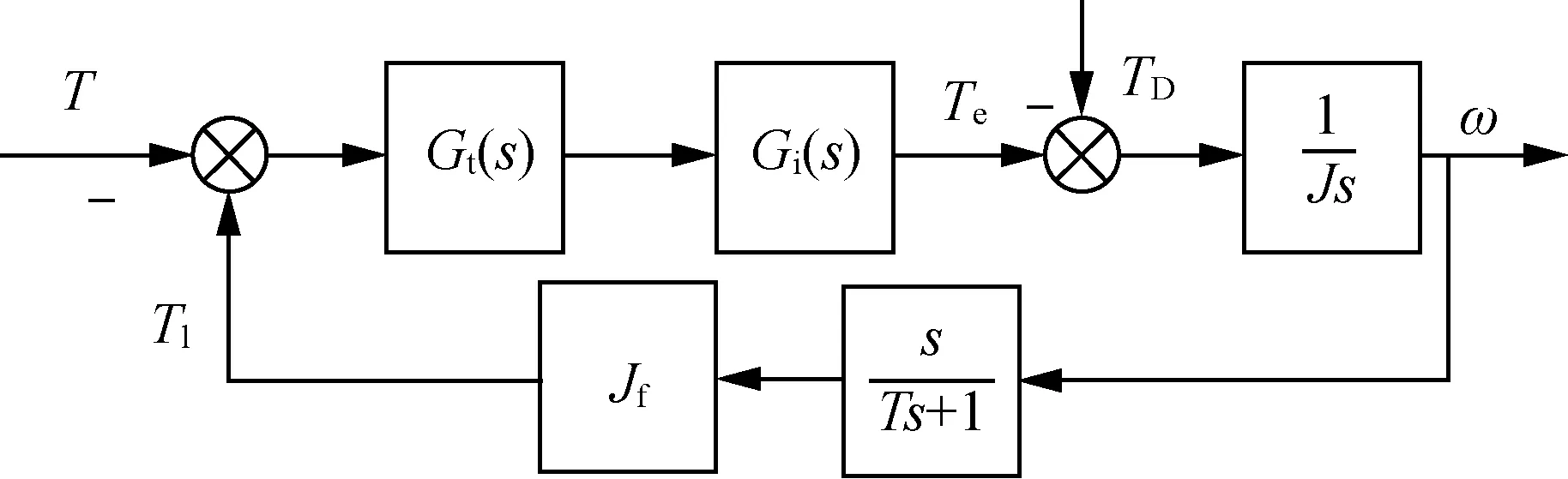
图5 扭矩控制结构Fig. 5 Torque control structure

Gi(s)为电流环动态特性，根据式(11)～式(14)可计算出相应扭矩Tl。惯性环节只是定量表示滤波方法，最终由自适应卡尔曼代替惯性环节。跟踪控制器Gt(s)采用比例积分(PI)控制器的形式以消除跟踪误差。

(21)

式中：Kp——比例系数；

K1——积分系数。

4 角加速度预测

4.1 测频精度确定

由上述可知逆模型控制中非惯性负载与速度线性相关且与速度导数无关，实际模拟时易实现；实际速度测量误差及微分项噪声导致惯性负载计算不易实现，负载模拟难度也在于此，这就对系统采样频率和测频精度有一定要求。

C8051F120型号单片机速率高达100MIPS，具有16×16硬件乘法、12位ADC等。基于该型号单片机对负载电机编码器获取的脉冲信号进而得到转速信号，所能达到100 Hz采样频率对应转速测频精度为0.01%和0.001%；后续在Matlab/Simulink分别对不同测频精度进行相应分析。

4.2 PI自适应卡尔曼滤波

系统的运动参数主要包含转速及轴角加速度。从测量参数到最终加载部分进行加载输出，这一系列过程中角加速度含有大量噪声，精度和滞后二者不能同时保证。这就要求在尽可能准确滤波效果的前提下保证角加速度的实时精度[19-20]。可结合最优转速测频精度和自适应卡尔曼滤波，在得到良好的滤波效果的同时预测角加速度下一步最优状态。

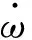
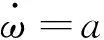
(22)

考虑噪声后的状态方程

xk=Ak-1xk-1+w

(23)

yk=Cxk+v

(24)

式中：A——状态转移矩阵；

C——观测矩阵；

w——过程噪声；

v——测量噪声。

噪声均值及方差

E(w)=E(v)=0

(25)

E(wwT)=Qa

(26)

E(vvT)=Ra

(27)

式中：Qa——过程噪声协方差；

Ra——测量噪声协方差；

E(w)——过程噪声均值；

E(v)——测量噪声均值。

状态第一步预测

(28)

协方差预测

(29)

增益计算

(30)

更新估计

(32)

更新协方差

(31)

用时变观测协方差矩阵Rk代替上述中的Ra则有

Rk=(1+αk)Rk-1

(33)

定义残差方差理论值

(34)

定义残差方差实际值

(35)

残差差值

Ek=trace(Dk)-trace(Qk)

(36)

调整系数

(37)

自适应卡尔曼则是通过PI控制残差方差来计算调整系数αk，并以此来调整Rk。

5 仿真分析

根据上述分析，系统控制方案如图6所示。转速信号微分后由PI卡尔曼在不同采样频率和测频精度下进行角加速度处理，最后经逆模型控制计算得到转矩命令发送给电机控制器，控制负载电机实时进行动态加载，使得被测模拟点端工作状态与实际运行情况保持一致。

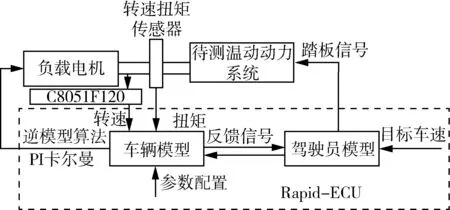
图6 系统控制方案Fig. 6 System control scheme

为验证台架逆模型负载模拟方法可行性，在Matlab/Simulink中进行仿真试验，本试验选在电机输出端作为负载模拟点，整车仿真参数如表1所示。

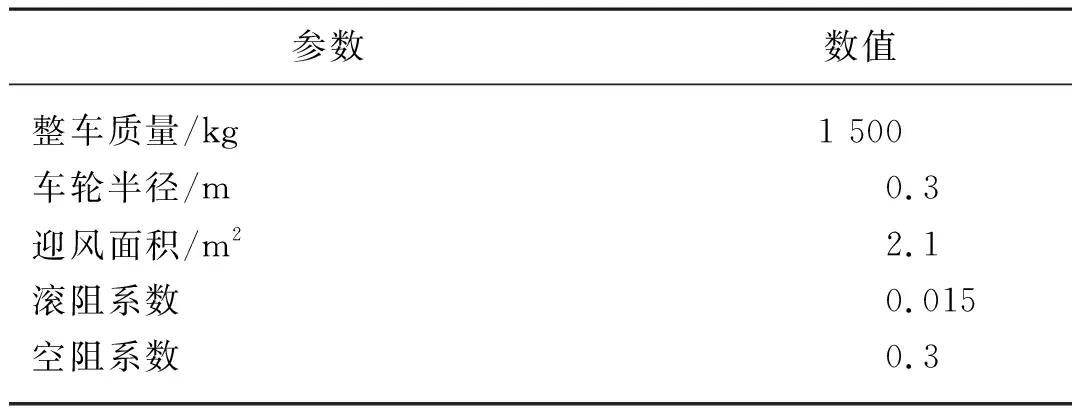
表1 整车参数Tab. 1 Vehicle parameters

首先分析采样频率对负载模拟的影响，以NEDC工况进行模拟测试，如图7所示。为更好对比不同采样频率下电机加载转速和扭矩，以NEDC前100 s转速为例，对比1 Hz、100 Hz不同采样频率下电机加载转速和扭矩，结果如图8、图9所示。可以看出加速至匀速阶段和匀速至减速阶段，低采样频率下电机实际转速有一定波动，电机实际扭矩响应较慢且与理论值相差较大。随着采样频率的增大，电机实际转速与目标转速越接近，电机实际扭矩与理论计算扭矩越接近；采样频率100 Hz时负载模拟精度较高。

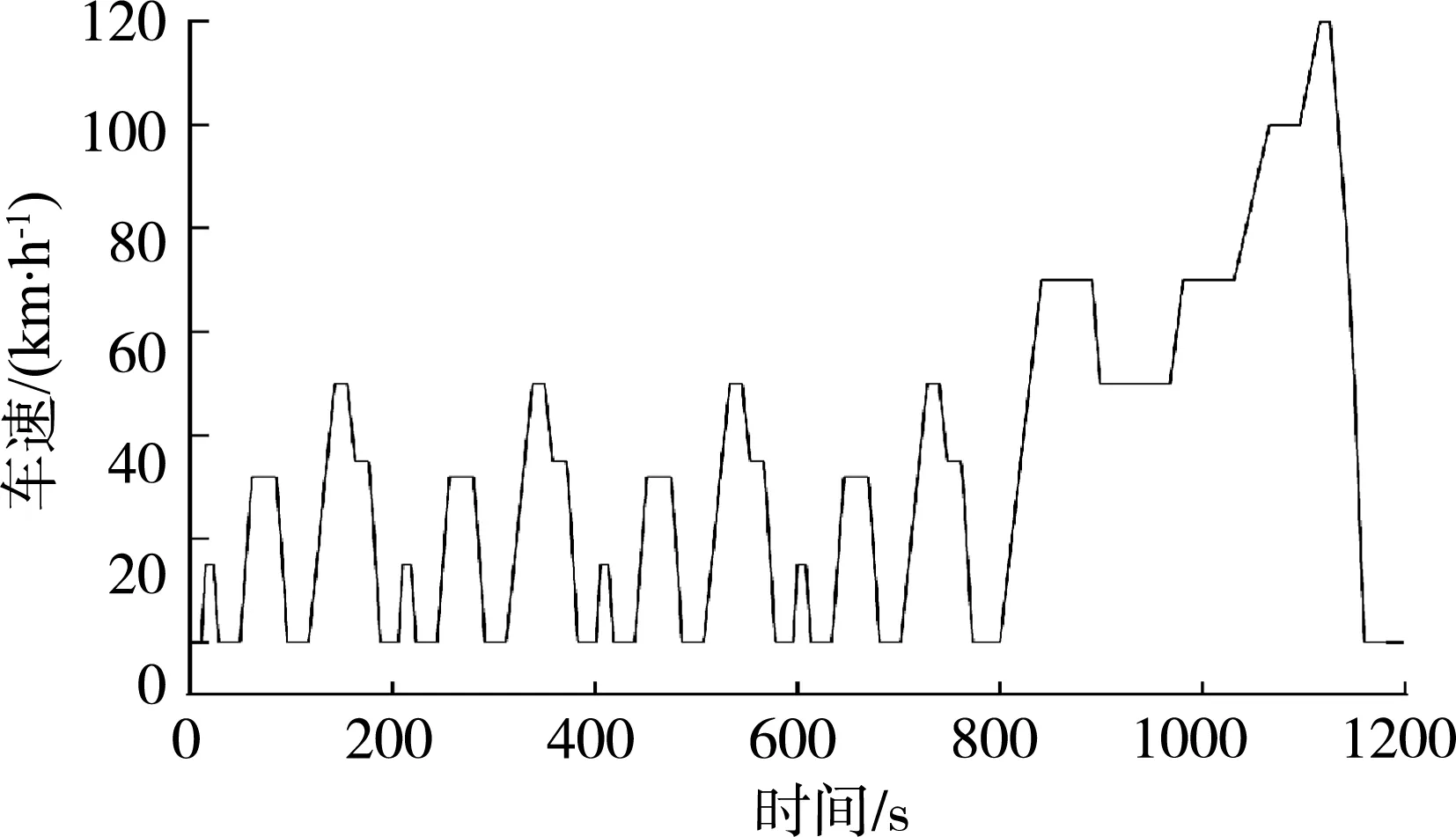
图7 NEDC工况曲线Fig. 7 NEDC operating condition curve

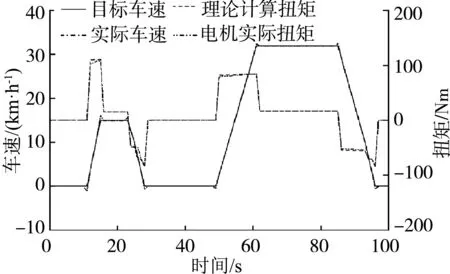
图8 采样频率1 Hz电机实际转速扭矩曲线Fig. 8 Actual speed and torque curve of the motor with a sampling frequency of 1 Hz

图9 采样频率100 Hz电机实际转速扭矩曲线Fig. 9 Actual speed and torque curve of the motor with a sampling frequency of 100 Hz

选取WLTC工况在100 Hz采样频率下再次进行模拟测试，其结果如图10～图12所示。

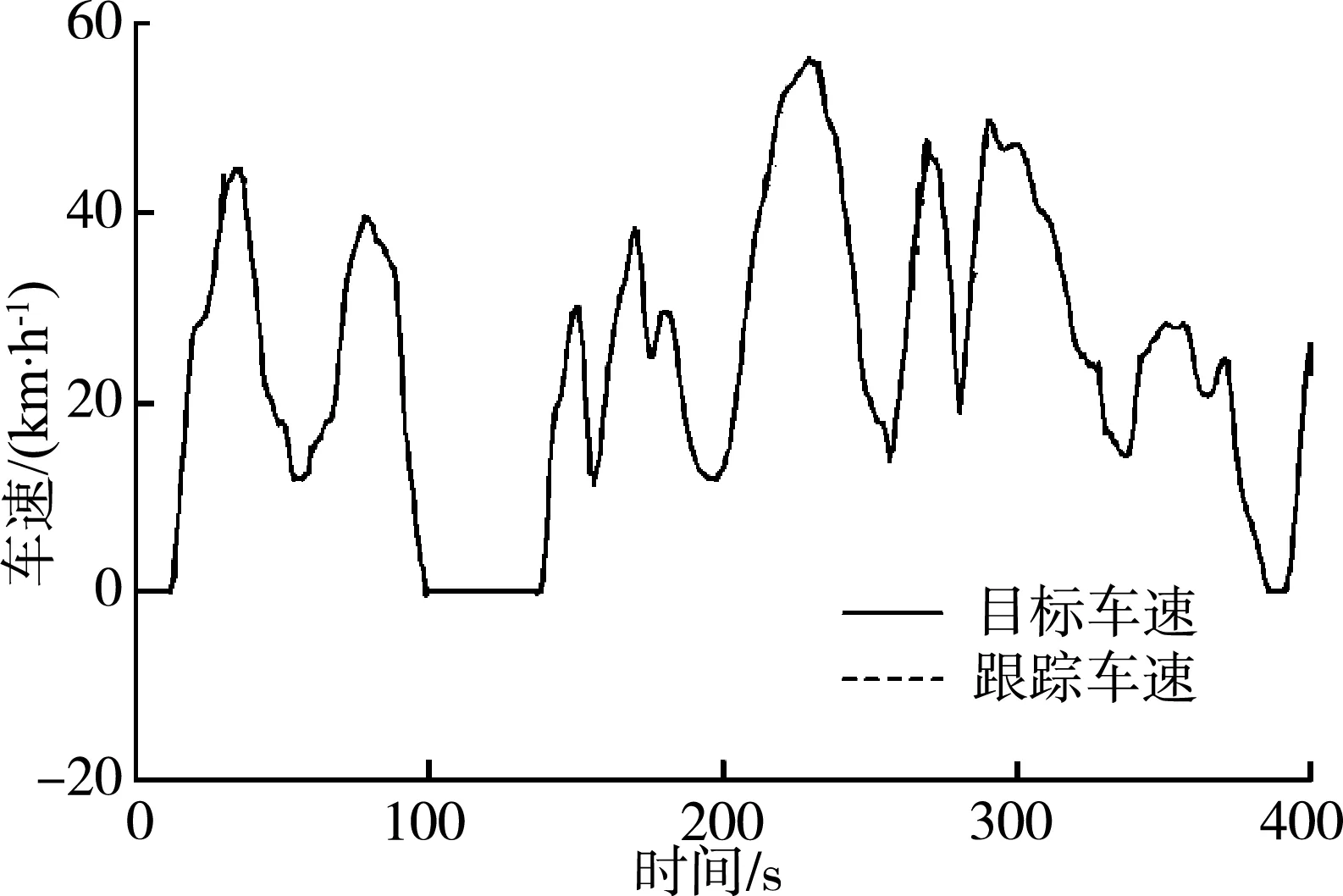
图10 WLTC工况车速曲线Fig. 10 Vehicle speed curve in WLTC working condition

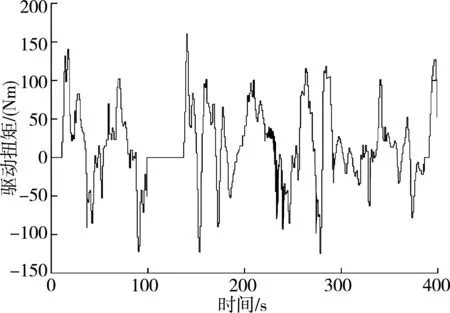
图11 WLTC驱动扭矩曲线Fig. 11 WLTC drive torque curve

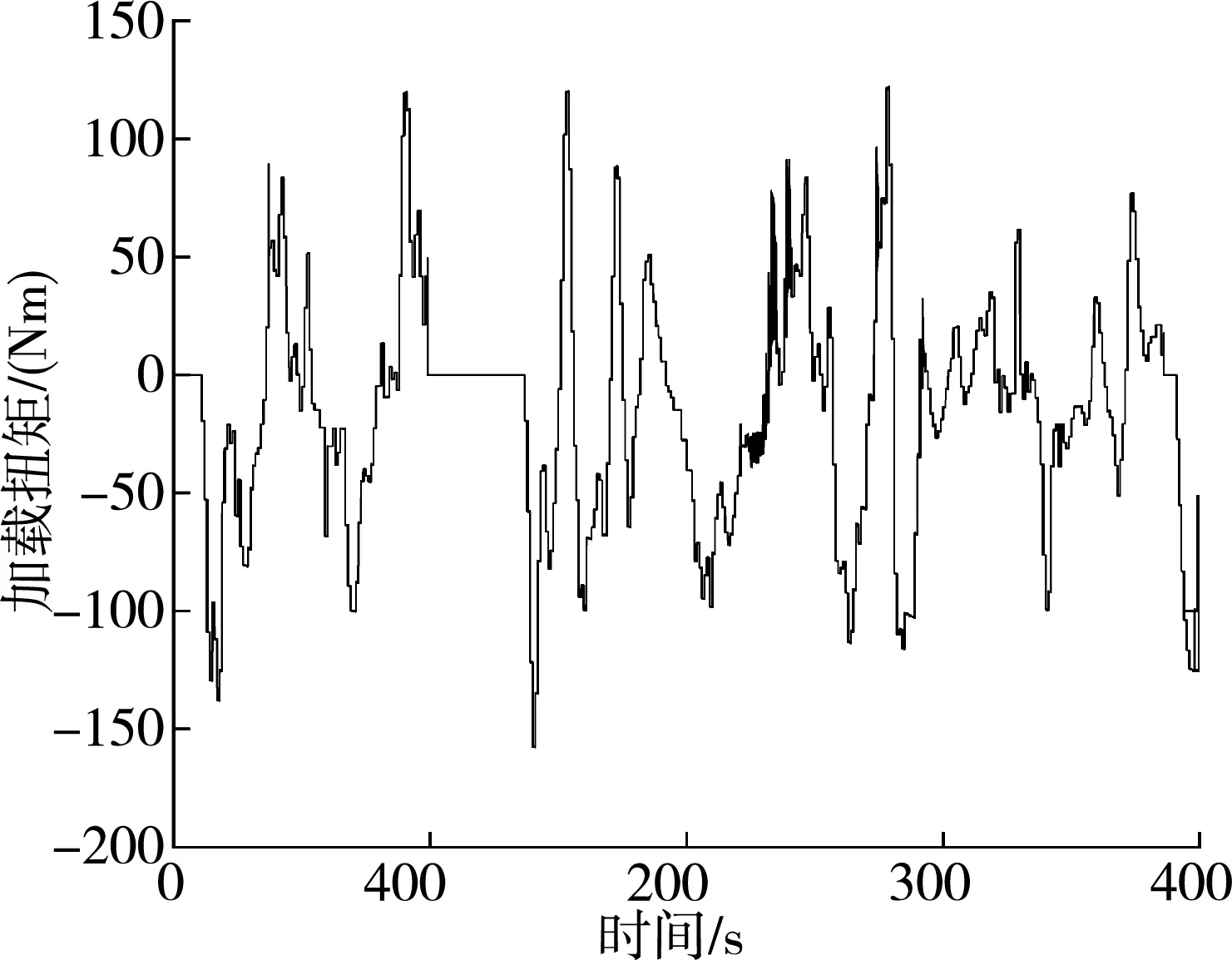
图12 WLTC加载扭矩曲线Fig. 12 WLTC loading torque curve

可以看出在100 Hz下转速跟踪较好，加载扭矩实际方向与驱动扭矩方向相反，驱动扭矩与加载扭矩相差不大，再次说明了100 Hz采样频率下能够达到负载模拟效果。此外影响负载精度的另一个因素是系统的测频精度。低速段以NEDC前100 s，最大转速32 km/h为例，高速段以郊区工况，最大转速120 km/h为例。在采样频率100 Hz情况下对比0.01%和0.001%不同测频精度下的角加速度结果。令C=1，A=0，可得到的低速段角加速度曲线，如图13、图15所示；高速段角加速度曲线，如图14、图17所示。

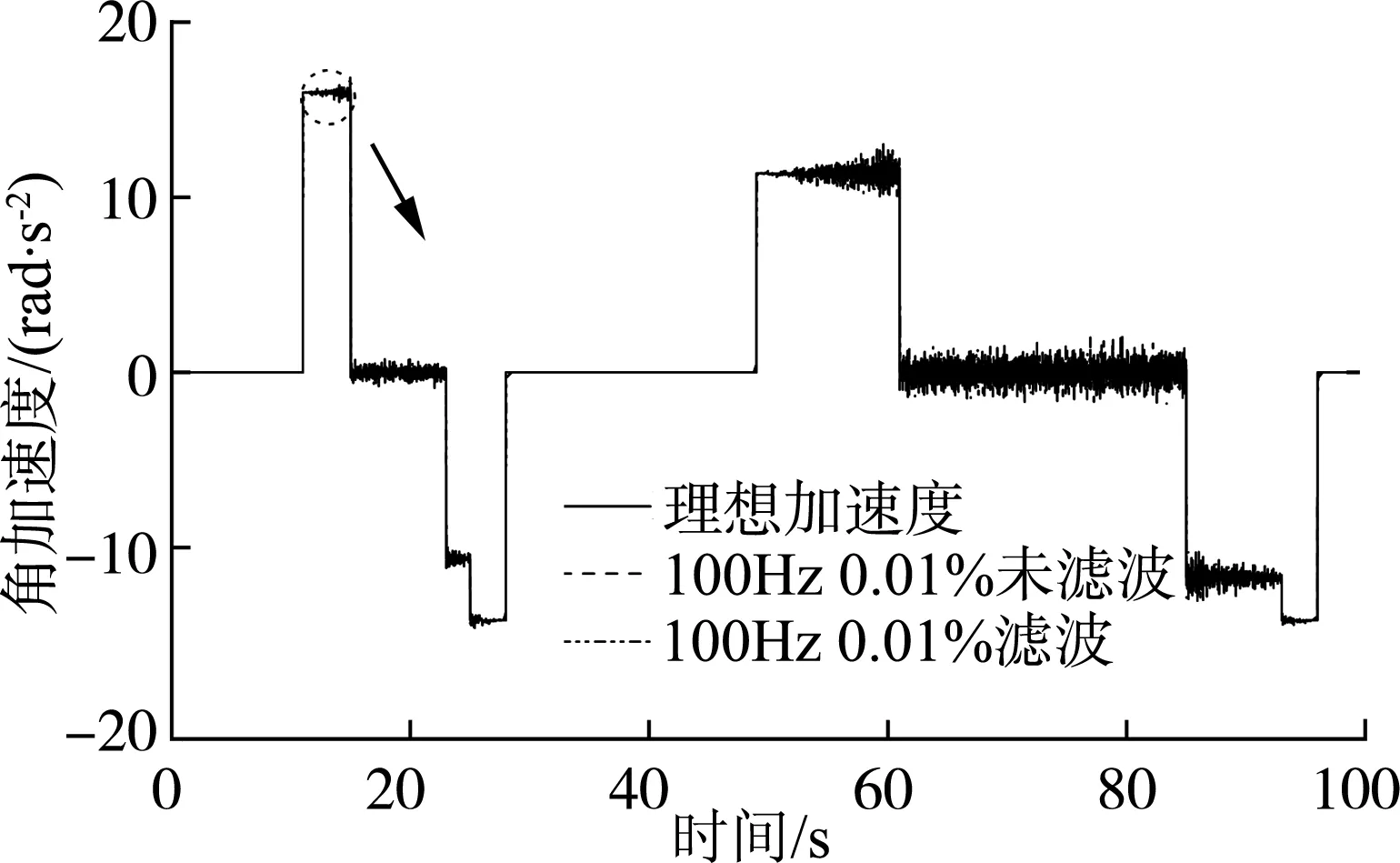
图13 采样频率100 Hz，测频精度0.01%低速段角加速度曲线Fig. 13 Sampling frequency 100 Hz, frequency measurement accuracy 0.01% low-speed angular acceleration curve

图14 采样频率100 Hz，测频精度0.01%高速段角加速度曲线Fig. 14 Sampling frequency 100 Hz, frequency measurement accuracy 0.01%, high-speed section angular acceleration curve

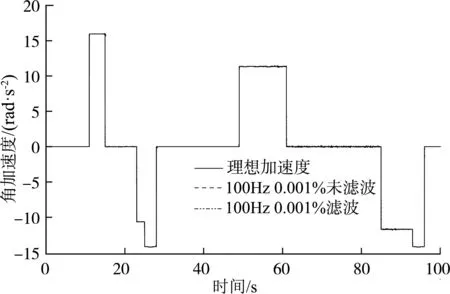
图15 采样频率100 Hz，测频精度0.001%低速段的角加速度曲线Fig. 15 Angular acceleration curve of low-speed section with sampling frequency of 100 Hz and frequency measurement accuracy of 0.001%

实时计算当前扭矩与传感器实测扭矩进行闭环扭矩控制，并将输出值给到电机控制器中(设置成扭矩模式)；调节控制器参数从而控制电机加载到目标曲线，得到负载电机实际扭矩，如图16、图18所示。

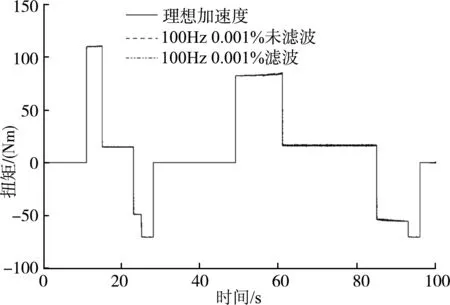
图16 采样频率100 Hz，测频精度0.001%的低速段的电机加载扭矩曲线Fig. 16 Motor loading torque curve in the low-speed section with a sampling frequency of 100 Hz and a frequency measurement accuracy of 0.001%

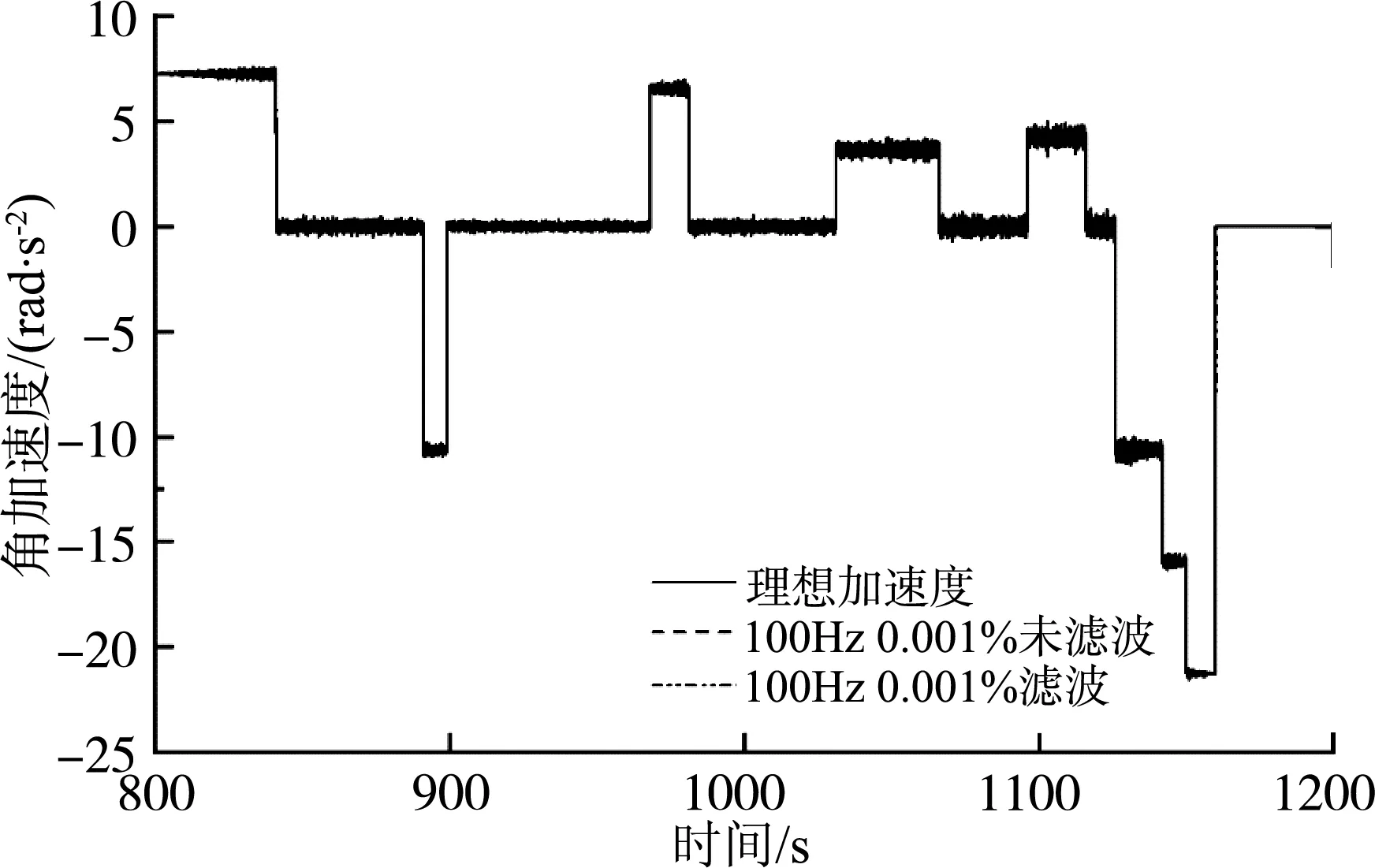
图17 采样频率100 Hz，测频精度0.001%高速段的角加速度曲线Fig. 17 Angular acceleration curve of high-speed section with sampling frequency of 100 Hz and frequency measurement accuracy of 0.001%

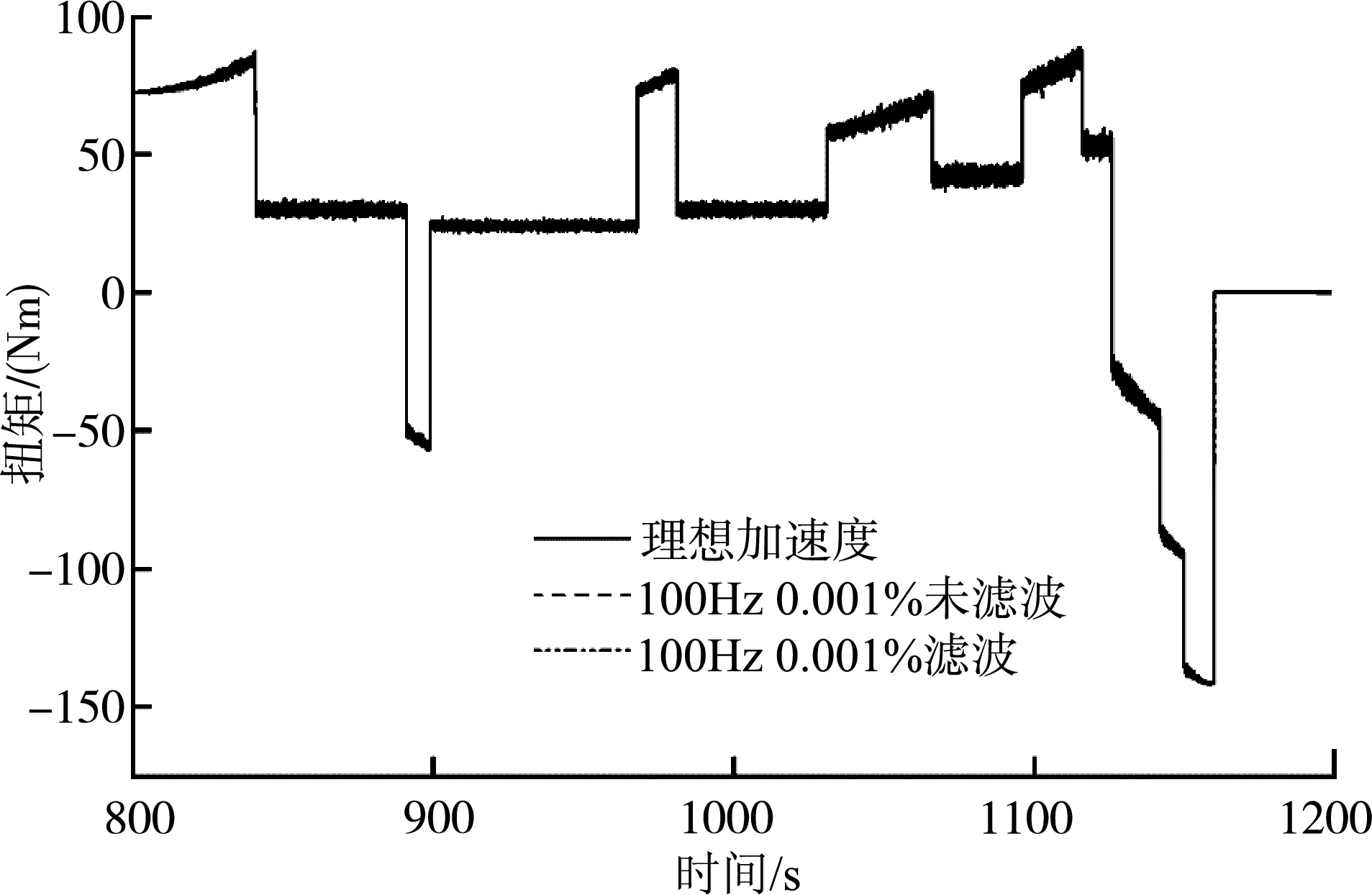
图18 采样频率100 Hz，测频精度0.001%高速段电机加载扭矩对比Fig. 18 Sampling frequency 100 Hz, frequency measurement accuracy 0.001%, high-speed motor load torque comparison

可以看出，低转速时角加速度和扭矩误差小，随着转速升高加速度和扭矩误差大。在低速段和高速段，测频精度0.001%方案都比0.01%方案下效果好，角加速度更加接近理想值。在低速段，因角加速度和扭矩误差小，所以测频精度0.001%下滤波后的结果比滤波前结果相差不大且滤波后会存在时间滞后；而在高速段角加速度和扭矩误差大，所以需要进行滤波处理。其结果如表2所示。在低速段，测频精度0.001%未滤波下最大扭矩误差在10%内；高速段经滤波后，动态扭矩响应时间为0.11 s，扭矩误差15%，满足台架测试要求，可以达到良好的负载模拟效果。

6 结论

本文针对试验动力台架需求，提出一种逆模型实时模拟负载的控制方法，设计了相应的控制器；搭建系统各部分模型，应用PI卡尔曼滤波对角加速度进行最优估计且分析系统了不同采样频率和测频精度对负载模拟的影响；结果表明，在低速段采样频率100 Hz、测频精度0.001%未滤波，扭矩误差10%；高速段采样频率100 Hz、测频精度0.001%滤波，动态响应时间0.11 s，扭矩误差15%，可以达到良好的模拟效果；该结果为硬件在环测试提供了理论依据。