随机约束满足问题相变研究综述*
2022-08-11牛鹏飞王晓峰张九龙
牛鹏飞,王晓峰,2,芦 磊,张九龙
(1.北方民族大学计算机科学与工程学院,宁夏 银川 750021; 2.北方民族大学图像图形智能处理国家民委重点实验室,宁夏 银川 750021)
1 引言
随机约束满足问题RCSPs(Random Constraint Satisfaction Problems)由一组变量和变量的约束条件组成。对约束满足问题求解就是对所有变量寻求一组赋值使得所有约束条件都被满足的过程。该问题在模式识别、时序推理和机器人路线规划等应用广泛。理论计算机科学和人工智能领域很多NP-完全问题本质上都可用约束满足问题来表示,因此,研究约束满足问题具有很强的理论意义和实际应用价值。对约束满足问题进行深入研究不仅可以探索该问题难解的原因,还可以从统计物理学和数学等交叉方向解析约束满足问题相变现象的本质,并据此为设计高效的求解算法奠定理论基础[1]。
1991年,Cheeseman等[2]发现在约束满足问题中存在约束密度,随着约束密度的不断增大,RCSPs会发生可满足相变现象。之后文献[3]揭示了随机约束满足问题的解空间变化更为复杂,在可满足相变之前,会依次发生聚类相变、冷凝相变和刚性相变等几类不可满足相变现象,这说明相变点附近不仅包含问题最难解的实例,而且在这几个相变点附近,解空间的结构特征具有不同的代数统计性质和几何统计性质。
随机图着色问题和随机可满足问题是随机约束满足问题中最重要的2个子问题,其中随机可满足问题是第一个被证明的NP-完全问题[4],随机图着色问题也是经典的组合优化问题。对随机图着色问题和随机可满足问题相变的研究主要是通过数值计算及算法分析、严格数学分析和统计物理分析3种不同思路的方法来展开的。
本文对近几十年来随机图着色问题和随机可满足问题相变研究的相关成果进行了汇总。其中,第2节介绍随机图着色问题及其相关定义,对随机图着色问题的可满足相变和不可满足相变进行详细综述;第3节介绍随机可满足问题及其相关定义,对随机可满足问题的可满足相变和不可满足相变进行汇总;最后对随机约束满足问题未来的研究趋势进行展望。
2 随机图着色的相变问题
给定一个无向图G(V,E),其中,V为顶点集合,E为边集合,图着色问题是指用q种颜色对顶点着色,并满足V中任意2个相邻顶点颜色不同,即将顶点集合划分为q个独立集。
2.1 相关定义
随机图理论作为图论的重要分支,是由Erdös等[5]在1959年引入随机图生成模型Gn,p而产生的。Gn,p模型中的参数n表示随机图的顶点个数,参数p表示随机图中任意2个顶点间以概率p相连。在该模型中,任意2个顶点之间是否存在边的概率是独立计算的,因此便于采用解析方法对其研究[6]。近几十年,针对图着色问题,研究人员已经从计算复杂性分析、色数、相变现象和求解算法等多个角度进行了大量的研究,并发现给定随机图的平均顶点度d=np,当d小于相变点Cs时,随机图高概率可着色,当d大于相变点Cs时,随机图高概率不可着色。

图1为约束密度增大时几类相变出现的位置以及解空间的变化情况。当顶点连通性很低时,所有解都出现在一个大解簇中,解与解的汉明距离很小,很容易从一个解“转移”到另一个解;当连通性稍微增加时,解的相空间分解成指数级数量的簇。随着约束密度的增加,解空间将依次经历以下几类不满足相变。

Figure 1 The change trend of solution space of random constraint satisfaction problems with constraint density图1 随机约束满足问题解空间随约束密度的变化示意图
2.2 随机图着色问题的不可满足相变
2.2.1 聚类相变
当图的顶点平均度达到相变点Cd时,随机图着色问题的解空间在结构上会发生变化,解空间的数目会突然增多,即解空间被分裂成数目众多的子空间,每个子空间包含一定数目的解,但不同子空间的统计性质各不相同,且不同子空间解的相似度远远低于同一个子空间解的相似度。这一突变被称为聚类相变,这个相变点Cd被称为聚类相变点或动态转移相变点。统计物理学认为聚类相变是由解簇上自旋变量之间的某些长程相关性引起的,这种相关性不是通常的两点函数,而是点到集合的相关函数。2007年,Zdeborová等[12]得到随机图着色问题聚类相变点的渐进值,如式(1)所示:
Cd=k(lnq-ln lnq+1+o(1))
(1)
聚类相变也对应着一个信息理论问题的转移,称为树重构相变点。Budzynski等[13]通过求解树重构相变点得到了随机图着色问题聚类相变点新的渐进值,如式(2)所示:
Cd=qlnq+ln lnq+γd+o(1))
(2)
其中,γd=0.812,表1为q=3时,随机图着色问题的聚类相变点的研究成果。

Table 1 Clustering phase transition point of random coloring problem when q=3表1 3-随机图着色问题聚类相变点
2.2.2 冷凝相变
当约束密度超过Cd到达另一个相变点Cc时,随机图着色问题的解空间进一步变化,解空间的统计性质开始由那些包含微观构型最多但是数目较少的子空间决定,此时解空间仍然有指数级数量的聚类解簇,并且这些聚类解簇之间彼此有较好的分离,这个变化现象被称为冷凝相变。冷凝相变也是随机约束满足问题相变研究中的热点。通过空腔法证实在可满足相变点之前解空间会发生冷凝相变,标志着解空间几何结构的进一步变化。冷凝现象似乎是解决各种问题的关键,包括寻找q色相变点和严格分析信息传播算法。Zdeborová等[12]给出了随机图着色问题冷凝相变点的渐进值,如式(3)所示:
Cc=2qlnq-lnq-2 ln 2+o(1)
(3)
目前最好的冷凝相变点渐进值是Bapst等[18]给出的,如式(4)所示:
Cc=(2q-1)lnq-2 ln 2+εq
(4)
当q→∞时,εq→0。Bapst等[18]证明了在随机图着色问题中确实发生了冷凝相变,并且发生在空腔法预测的精确位置上。这也是第一个通过严格证明得到的随机图着色问题的冷凝相变点。
2.2.3 刚性相变
若约束密度超过变相点Cc,随机图着色问题的解空间将发生另一种重要的相变:有限部分的冻结变量出现在占优势的解簇中时,刚性相变发生,这个相变点Cr被称为刚性相变点。刚性相变点是动态相变点,刚性相变可能发生在冷凝相变之前,也可能发生在冷凝相变之后。Zdeborová等[12]首次分析了这种相变现象,并给出了随机图着色问题刚性相变点的渐进值,如式(5)所示:
Cr=q(lnq+ln lnq+1+o(1))
(5)
此后,Molloy[19]在文献[12]的基础上得到刚性相变点新的渐进值,如式(6)所示:
(6)
2.3 随机图着色问题的可满足相变
随机图着色问题相变研究最多的是可满足相变,但直接求解可满足相变点是困难的,因此,研究人员通过对上下界的改进不断逼近可着色相变点,并取得了一系列丰硕成果。2004年,Krząkaa等[16]通过1RSB得到了随机图着色问题可着色相变点的下界,如式(7)所示:
Cs≥2qlnq-lnq-2+oq(1)
(7)
当q→∞时,oq(1)→0。与此同时,Achlioptas等[7]首次通过二阶矩方法得到了随机图着色问题可着色相变点下界的渐进值,如式(8)所示:
2qlnq-2 lnq-2+oq(1)
(8)
2007年,Zdeborová 等[12]得到随机图着色问题可着色相变点的渐进值,如式(9)所示:
Cs=2qlnq-lnq-1+o(1)
(9)
Coja-Oghlan等[20]对可着色相变点下界的渐进值进一步改进得到式(10):
Cc=2qlnq-lnq-2 ln 2
(10)
Cc为随机图着色问题的冷凝相变点,最早关于随机图着色问题可着色相变点上界的渐进值,如式(11)所示:

(11)
Coja-Oghlan[21]对可着色相变点上界的渐进值进一步改进得到式(12):

(12)
可以观察到上述文献中相变点上下界的差值为2 ln 2-1+o(1)。相较于以往研究人员得到的可着色问题相变点上下界的差值会随着q的增长不断增大,2 ln 2-1+o(1)是目前可着色问题相变点上下界的最小差值。q=3的随机图着色相变点的研究进展,与q为任意值的时候有很大的联系,但也有些区别。总体概括如表2所示。
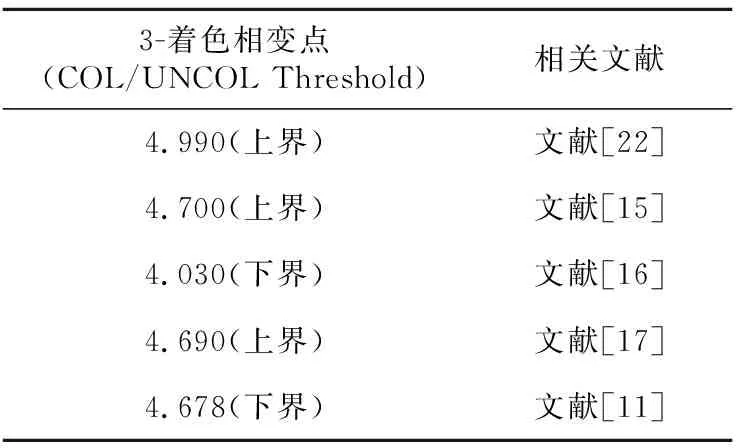
Table 2 Coloring phase transition point of random coloring problem when q=3表2 3-随机图着色问题可着色相变点
3 随机可满足问题的相变
可满足问题SAT(SATisfiability problem)是最具有代表意义的约束满足问题。给定一个合取范式CNF(Conjunctive Normal Formula)F,本文用1和0表示随机变元的true和false 。判定是否有一组布尔变元的指派真值指派x∈{0,1}n使F为真,这个判定问题就是SAT问题。长期以来SAT问题在人工智能和理论计算机科学中都是一个核心问题。
3.1 相关定义
每个子句长度均为k的SAT问题被称为k-SAT问题,称随机k-SAT模型生成的实例为随机k-SAT公式。虽然已经有很多性能优异的算法能够求解变元规模很大的随机k-SAT问题,但不论是完备求解算法还是非完备求解算法都仍有局限性。随着约束密度不断增大,这些算法会逐渐失效。这种现象激发了人们的研究兴趣,研究人员揭示了计算复杂性与相变现象存在密切联系,有学者认为NP-完全问题的相变研究是计算复杂性理论研究的延续,相变现象更直接、更细致地展示了约束满足问题难解的本质。
3.2 随机可满足问题的不可满足相变
在对随机k-SAT问题的研究过程中,相变中解空间的变化与随机k-SAT问题难解关系密切。由于统计物理学中对解空间结构分析的假设和方法的引入,对随机k-SAT问题的不满足相变的研究在近些年取得了很多突破性成果[23]。
3.2.1 聚类相变

3.2.2 冷凝相变

(13)
3.3 随机可满足问题的可满足相变
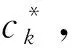
(1)算法研究。
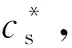
(14)
因为任意的SAT问题都能在多项式时间内规约到k-SAT问题,而随机3-SAT问题是最简单的NP-完全问题,因此对随机3-SAT问题的相变研究具有特殊性和代表性,难解实例是在C3=4.25附近出现的,该相变点是基于回溯的DPLL算法的平均计算时间来刻画的[30]。
研究人员发现可以通过算法实验来得到相变点的下界。Crawford等[31]的研究结果表明,随机3-SAT问题的数值实验显示相变点C3≈4.258。此后,Monasson等[32]通过实验得到随机3-SAT问题更新的相变点C3≈4.27。Mann等[33]通过“弹道网络方法”克服了一般局部搜索算法容易陷入局部最优的问题,得到了C3≈4.267。对于随机3-SAT问题的算法实验表明相变点C3≈4.3。Kirkpatrick等[34]首次给出了k-SAT问题可满足相变的相变点算法估计,运用完全算法估计方法得到C3≈4.17。
Chao等[35]通过设计算法一次一个地对文字进行赋值,直到找到一个解,或者发现进一步的赋值导致不能找到一个解。具体流程为:使用单位子句规则作为选择下一个文字的启发式策略,在每一步中,从包含最少数量文字的子句中随机选择一个文字进行赋值。进而求得随机3-SAT问题可满足相变点的下界为2.99。Chvátal等[36]将这一结果提升到2.67。Broder等[37]设计了基于纯文字规则的启发式算法,求得新的随机3-SAT问题可满足相变点的下界为1.63。此后,Frieze等[38]通过求解算法中的确切极限概率求得了新的下界为3.003,基于此,Achlioptas[39]在2000年提出了一种新的启发式算法,并运用微分方程分析了算法,得到新的下界为3.145。之后Achlioptas等[40]又将下界的值提升到3.26。Kaporis等[41]设计了一种新的启发式算法,得到新的随机3-SAT问题可满足相变点的下界为3.42。截止目前,随机3-SAT问题可满足相变点下界的最好结果是由Kaporis等[42]通过提出的一种启发式算法得到的,该算法得到的相变点下界为3.52。当k=4时,Gent等[43]得到可满足性相变点C4≈9.8。
本文中所提到的随机3-SAT问题可满足相变点下界的研究结果汇总如表3所示。

Table 3 Lower SAT/UNSAT threshold of random 3-SAT problem表3 随机3-SAT问题可满足相变点下界

(15)
由于NP问题的高度计算复杂性,在问题规模较大时,通过算法实验和数值模拟的方法设计高效算法是困难的。因此,在算法实验中估计出来的可满足相变点,当问题规模较小时可能比较准确,当规模较大时估计值误差较大。
(2)统计物理。
在统计物理学中,随机k-SAT问题等效于随机无序系统中的自旋玻璃,所以统计物理学在SAT问题的研究过程中表现相当活跃。对随机k-SAT问题的研究可以纳入到统计力学的研究框架中。下面从统计力学的角度综述随机k-SAT问题的研究成果。
通过统计物理学的有限尺寸缩放技术得到k=3,4,5,6时的可满足相变点。在极限情况下,文献[34]用一个简单的概率给出了可满足相变点的渐近表达式Cc≃2kln 2。Monasson等[47]使用一阶复本对称方法对随机k-SAT问题的可满足变相点进行了研究,发现复本方法并不能有效求解此问题,Monasson得到的渐进相变点如式(16)所示:
(16)
Mézard等[48]将统计物理学的自旋玻璃模型引入随机k-SAT问题的求解中,提出随机k-SAT问题的解空间“存在多个状态”,并利用统计物理学中的1RSB方法得到了随机3-SAT问题的可满足相变相变点为C3=4.256,并发现在可满足相变点之前的某个位置解空间分裂成了指数级数量的解簇以及解簇的扩散这2种现象。而且他们认为随机k-SAT问题难解的根本原因就是解空间分裂成指数级数量的小解簇。Mertens等[49]得到了随机k-SAT问题的可满足相变点是严格出现在几类不满足相变点之后的结论,这表明满足/不可满足相变点Cs始终处于稳定区域,且得到了可满足相变点的渐进表达式,如式(17)所示:
(17)
目前的统计物理得到的最好估计值C3=4.262[50]。一段时间内,一些难解问题都通过统计物理学的方法得到了很好的解决,人们对约束满足问题相变成因的认识也更为清晰。但是,随着研究的深入,研究人员发现对于更多的随机约束满足问题,1RSB方法得到的相变点要比算法得到的极限点更小,因而研究人员开始重新考虑1RSB方法与求解问题难解性之间的关系。直至2007年,Zdeborov等[12]应用基于能量和熵观点的landscape分析方法对解空间中占据主导地位的解簇进行了研究,推动了一系列对约束满足问题相变现象的本质研究。随着统计物理学在随机约束满足问题相变领域表现出强大生命力,产生了一系列重量级成果,以统计物理为核心研究技术的方向逐渐形成了一套比较完善的体系。但是,理论物理学对随机k-SAT问题相变现象的大量研究成果都是基于物理学假设,因此其本身仍有一定的局限性。
(3)理论分析。
Franco等[51]在1983年利用最基本的一阶矩方法首次给出了随机3-SAT问题的上界为5.191,之后Maftouhi等[52]通过对一阶矩进行改进得到了新的上界为5.081。Kamath等[53]运用球与箱子模型来生成随机3-SAT实例并得到新的上界为4.758。Dubois等[54]得到随机3-SAT新的上界为4.643。Kirousis等[55]通过CNF公式中一个随机变量的递减序列,得到了随机3-SAT新的上界为4.602。Janson等[56]对文献[51]中得到的所有真值赋值求和,这个和被重新表述为由n个点组成的自旋系统的配分函数,从而求得了随机3-SAT新的上界为4.596。Kaporis等[57]将局部最大满足真值分配方法与占用问题概率的结果相结合,求得了不满足相变点小于4.571。Dubois等[58]通过提出一种新的矩方法得到了随机3-SAT问题的上界为4.506。目前关于随机3-SAT问题可满足相变点最好的结果是4.484 9,是由Díaz等[59]使用概率方法得到的。
本文中所提到的随机3-SAT问题可满足相变点上界的研究结果汇总,如表4所示。
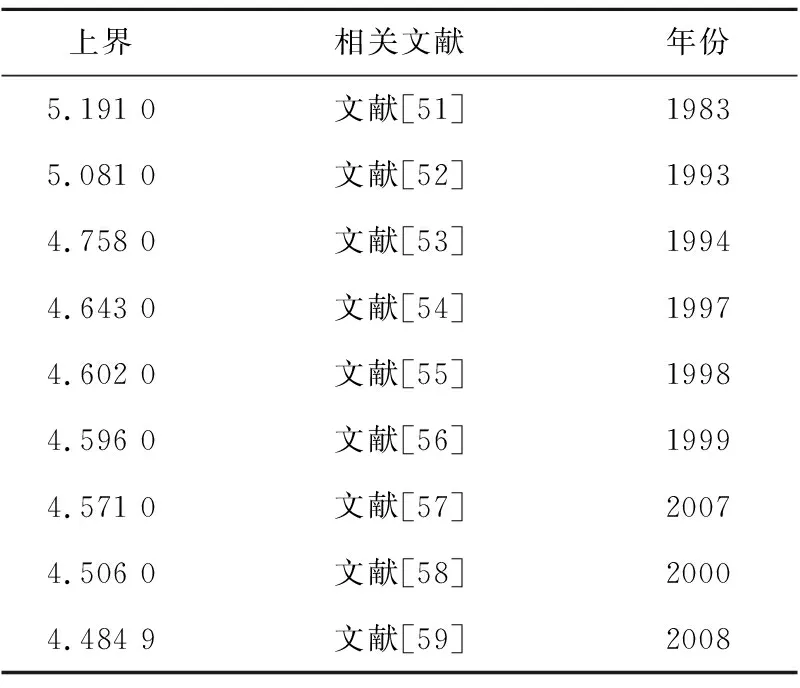
Table 4 Upper SAT/UNSAT threshold of random 3-SAT problem表4 随机3-SAT问题可满足相变点上界
对于任意k-SAT问题,Kaporis等[57]通过一阶矩方法得到了随机k-SAT问题可满足相变点上界,如式(18)所示:

(18)
Achlioptas等[60]通过二阶矩方法得到一个下界,如式(19)所示:
(19)
Achlioptas等[61]通过对二阶矩方法进行改进,提出了一种新的加权方式,如式(20)所示:
(20)
其中,c表示随机k-SAT问题对应的合取范式,u表示在赋值σ下文字被满足的个数,λ>0。通过这种改进得到了新的相变点下界,如式(21)所示:
(21)
基于此,刘军[62]提出了一种新的加权方法,如式(22)所示:
(22)
其中,β>-1,λ>0。
Coja-Oghlan等[63]得到了随机k-SAT问题可满足相变点新的下界,如式(23)所示:
(23)
之后,Coja-Oghlan等[64]得到随机k-SAT问题新的上下界,如式(24)所示:
(24)
2015年,Ding等[65]突破性地证明了当k充分大时,可满足相变点的正确性。证明存在一个常数k0,使得当k>k0时,随机k-SAT存在精确相变现象,且有:
Cs(n)=2kln 2-(1+ln 2)/2+ok(1)
(25)
4 结束语
随机图着色问题和随机可满足问题相变研究已经取得了一系列突破性进展,但现阶段并没有得到问题的精确相变点,我们认为未来的研究重要围绕以下几点:
(1)设计更加高效的启发式求解算法,得到更加精确的可满足性相变点。
(2)通过高阶复本对称破坏平均场理论刻画解空间结构,从而得到更加精确的可满足性相变点。
随机约束满足问题的相变研究与问题难解之间有紧密的联系,是理论计算机领域的重要课题之一。本文汇总了随机图着色问题和随机可满足问题的可满足相变和不可满足相变的国内外研究成果,并展望了未来的研究方向,以期对此领域相关的研究人员给予一定的帮助和启迪。
