基于MPI的并行大数据集生成器*
2022-08-11葛旭冉陈志广
葛旭冉,刘 洋,陈志广,肖 侬
(1.国防科技大学计算机学院,湖南 长沙 410073;2.中山大学计算机学院,广东 广州 510006)
1 引言
大数据时代大量企业需要处理的数据规模高达PB级甚至EB级,海量数据带来了海量价值,人们的生活方式越来越智能化。但是,数据规模的剧增也为传统的大数据处理平台和大数据处理分析算法带来了新的挑战,不断推动着技术改进和平台优化。另一方面,科技的高速发展使互联网用户对数据查询、分析、处理和响应的延迟要求越来越高,网络的实时性需求也持续增加。这些都导致传统大数据分析平台的处理能力与用户需求之间的鸿沟不断增大。例如,淘宝在“双十一”等重大节日时,经常会有页面卡顿、服务器崩溃等现象发生。对于这些企业而言,数据量大并不可怕,问题是如何实时处理海量数据,因为任何时延都可能会失去服务优势,进而引发企业用户的大量流失,从而导致商业经济下降。
为了解决上述问题,企业需要不断创新、研发新技术。在这个过程中,传统的大数据处理平台和大数据处理分析算法不断更新演进。然而,在这些大数据处理分析算法的优化研究过程中,速度常常受限于数据集规模。尤其是涉及到并行通信时,在数据集体量不足的情况下,算法的通信时间往往要高于真正的计算时间,进而难以验证算法本身的优化效果。因此,大规模集成数据是大数据处理优化研究的必要前提。但在现实生活中,往往难以找到适用于测试的大体量数据。为帮助其他大数据处理分析算法合理地测试性能和发现问题,需要自动生成一些满足分布条件的大规模随机数,并在此基础上建立可以控制数据规模和复杂性的人工测试数据集。
目前,国内外纷纷研究了应用于不同场合、不同环境的数据生成器[1]。在国外,Lo等人[2]提出了DBMS测试套件MyBenchmark和数据生成工具,以一组查询操作作为输入,生成数据库实例,同时用户还可以控制生成负载的特征; Houkjær等人[3]将数据表的生成转换成图的遍历过程,能够保证比较好的属性依赖和概率分布,但由于重点保持属性依赖,导致数据的并行化程度不高,降低了数据表的生成速度。在国内,中国科学院计算技术研究所的詹剑锋等人[4]提出了大数据测试基准BigDataBench,使用一个或多个数据模序组合来表示大数据和人工智能工作负载的多样性,其基准测试程序覆盖了多个大数据应用领域;顾伶等人[5]开发了一个流数据的分布式在线生成系统Chronos,可以由用户控制生成速度和吞吐量,并且在数据生成过程中能够保持属性之间的关联和时间依赖,生成满足流数据库测试套件的数据。
众所周知,大规模随机数生成器是产生复杂数据集的基础。目前,最常见的随机数生成器是基于线性同余算法LCG(Linear Congruential Generat- or)[6]实现的,被包含在大多数编程语言的随机数生成库中。LCG算法实现较为简单,但是产生数据的最低位具有相关性且序列周期相对较短。近年,MT(Mersenne Twister)方法逐渐流行起来,它可以产生周期较长的随机数序列,其MT19937变体可以产生周期为219937-1的离散型均匀分布随机数。但是,该方法实现较为复杂,并行化效率低且需要大量的缓冲器。因此,本文主要采用了线性同余算法生成均匀分布的伪随机数,然后通过各种函数变换及映射关系得到任意概率分布[7]的伪随机数,并在此基础上构造了并行伪随机数生成器。
本文将传统的随机数生成算法并行化,将整个任务分解成许多子任务在多个进程中并行运算,既要保证各处理器生成自己所需要的随机数子序列,又要减少处理器之间的通信负担,从而大大提高数据集生成规模和生成速度,帮助大数据处理分析算法进行性能测试和优化研究。
本文的主要贡献包括3个方面:
(1) 将LCG算法并行化生成符合均匀分布的伪随机数,然后通过各种函数变换及映射关系并行生成任意概率分布的随机数。
(2) 设计实现了不同用途的可以控制数据规模和统计属性的人工数据集生成算法,构造了一个通用的并行大数据集生成器,为运行在超级计算机上的并行大数据处理分析算法提供基准测试数据集。
(3) 研究实现了一个I/O系统,包括数据集的读、写操作,MPI-I/O读、写文件,生成不同数据格式的文件,分割数据集并将其分配到不同进程,以及设置映射规则使得所有节点之间都可以进行数据交互。
最后的实验结果表明,并行大数据集生成器有效提高了数据生成效率和生成规模,能够为大数据处理分析算法提供高质量、大体量的测试数据集。
2 背景
MPI并行编程是实现大数据集生成器的核心技术,生成满足不同概率分布条件的随机数是实现复杂人工数据集的前提。本节主要介绍MPI并行编程模型,以及生成均匀分布随机数的线性同余LCG算法和其他生成正态分布、泊松分布、多维正态分布、二项分布和多项分布等复杂分布随机数的算法。
2.1 MPI消息传递模型
MPI消息传递模型[8]面向分布式内存的单程序多数据并行计算机进行编程。常用的通信接口包括:MPI_Bast、MPI_Satter、MPI_Gather、MPI_Allgather、MPI_Allgatherall、MPI_Send、MPI_Recv和MPI_Barrier等。其基本思想是将一个大任务按照任务量或数据划分为若干个元任务,为了减少进程间的通信,合并适量的元任务,然后设置特定的映射规则将其分发到多个独立的进程中并行执行。在同一个通信器内,每个进程都有唯一的标识符rankID,通常,根据rankID编程控制各个进程运行相同或不同的代码块。根据程序的实际数据需要,调用MPI通信接口进行消息传递。通常的MPI程序结构如图1所示。
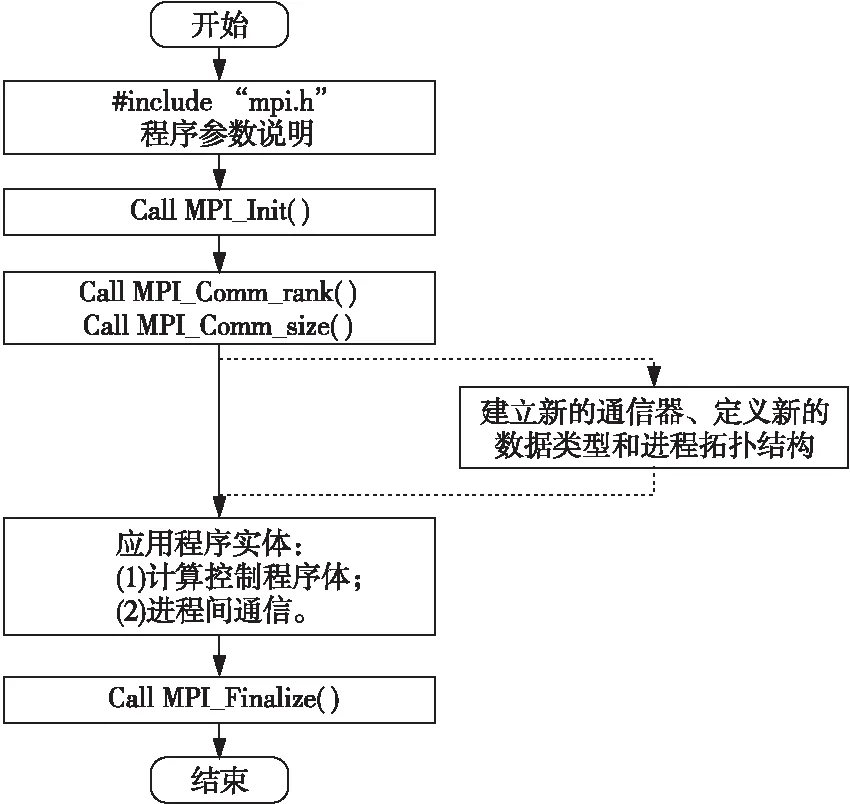
Figure 1 Framework of MPI parallel programming图1 MPI并行程序设计框架图
2.2 线性同余算法
线性同余算法是目前最流行的伪随机数[9 - 11]生成算法,其过程主要基于如式(1)所示的迭代公式:
Xi+1=(aXi+c) modm,i=0,1,…n,
m>0,0≤a (1) 其中,X0为随机数发生器的初始种子,a为乘数,c为增量,m为模数。由式(1)产生的随机序列并不总是随机的,它实际上是一个周期性序列。如果对于任意正整数i具有Xi+T=Xi,符合该条件的最小整数T为LCG序列的最大周期。但是,在实际情况下,它的周期要比m小。 c等于0时该随机数发生器的生成速度要比c不等于0时快。尽管c等于0时看起来缩短了随机数序列的周期长度,但它有很大概率获得较长的周期。起初,Lehmer[12]只提出了c等于0的情况,后来Thomson[13]和Rotenberg[14]发现:当c不等于0时,可以得到更长的周期。称c不等于0时的生成器为乘同余生成器;c等于0时的生成器为混合同余生成器。 (1)正态分布。Box-Muller变换的基本思想是使用2个符合均匀分布的随机变量构造符合高斯分布的随机变量。具体可以描述为:选取2个相互独立的在[0,1]上均匀分布的随机变量U和V,则符合均值为0、标准差为1的高斯分布随机变量X和Y如式(2)所示: (2) (2)多维正态分布。多维正态分布[15]的边缘分布仍然是正态分布,给定每个维度上边缘正态分布的均值mean和方差s,再加上相关系数矩阵cov,就可以得到它的联合概率分布P。算法具体步骤如下: ①根据边缘分布的均值mean和方差s,独立生成各个维度上的符合标准正态分布的随机数。将各个维度的随机数序列组合成一个向量X; ②将相关系数矩阵cov进行Cholesky分解得到下三角矩阵L; ③用分解得到的下三角矩阵L与向量X相乘,即可得到满足多维标准正态分布的随机数序列S。 (3)泊松分布。泊松分布[16]表示任意时刻都可能出现的一个事件在每个单位时间里出现的次数。假设离散随机变量X服从泊松分布,其概率密度函数如式(3)所示: (3) 其中,l等于离散随机变量X的均值和方差,k为随机事件发生的次数。 (4)二项分布。假设在n次伯努利实验中,每次实验成功的概率为p(0 0 (4) 其中,n为实验总次数,p为实验成功的概率,q为实验失败的概率。在实际模拟过程中,可以生成n个在[0,1]的随机数,统计其中大于p的数目即可得到符合二项分布的随机数。 (5)多项分布。多项分布是将二项分布的结果推广到多种状态得到的。如果把二项分布比作掷硬币,多项分布就类似于投骰子,骰子的6个面对应6个不同的点数,单次掷骰子每个点数朝上的概率都是1/6,重复扔n次。 假设某随机实验有r个可能结果A1,A2,…,Ar,每个结果出现的次数记为随机变量X1,X2,…,Xr,概率分布分别是p1,p2,…,pr,那么在t次采样的总结果中,A1出现t1次、A2出现t2次、…、Ar出现tr次的这种事件的出现概率P如式(5)所示: P(X1=t1,…,Xr=tr)= (5) Figure 2 Datasets for different purposes 图2 Dataset库中不同用途数据集 并行产生随机数的主要思路是使用同一个随机数生成器,各个进程分别产生随机数序列中不同的子序列。采用跳跃法将LCG算法并行化。 假设长度为L的原始序列为{X0,X1,…,Xi,…},总共有N个进程,进程i从Xi开始,每隔N个数取走1个数,进程i生成的序列为{Xi,Xi+N,Xi+2N,…},该序列中的下标代表进程i生成的随机数在原始序列中的位置。对于进程i来讲,可以构造该进程的混合同余递推公式,如式(6)所示: Yi,sub_i+1=(AYi,sub_i+C) modm (6) 其中,i=0,1,…,N-1,sub_i=0,1,2,…,各个进程的初始值{Y0,0,Y1,0,…,Yi,0,…,YN-1,0}为原始序列中的{X0,X1,…,Xi,…,XN-1}。A称为广义乘子,C称为广义增量,推导如式(7)所示: (7) 其中,a为乘子,c为增量,m为模数。 在实际计算中,可以采用式(8)来计算A: A=(…((a×amodm)× amodm)…×a) modm (8) 与分段并行方法相比,跳跃并行方法使用起来更加灵活,且各进程的初始种子容易计算。 人工大数据集的生成主要依赖于满足特定分布条件的随机数。这些数据集主要用于为运行在超级计算机上的并行大数据处理分析算法提供基准测试。通过调研大数据处理分析算法的实际需求,本文主要实现以下几类数据集:分类和聚类数据集、回归数据集、流形学习数据集和因子分解数据集,如图2所示。 将算法并行化的关键思路是拆解算法的循环部分,对其进行域分解,按照待生成数据集的样本总数为每个进程分配任务量。图2中17个数据集的生成算法虽各不相同,但其并行化思路相似。下面主要对聚类数据集make_gaussian_quantiles和因子分解数据集make_sparse__spd_matrix的生成算法并行化进行详细说明。 Figure 3 Parallel diagram of make_gaussian_quantiles algorithm图3 make_gaussian_quantiles算法并行示意图 3.2.1 make_gaussian_quantiles算法 make_gaussian_quantiles算法生成符合多维标准正态分布的各向同性单高斯簇,通过分位点定义由嵌套的同心多维球体分隔的类,以使每个类中的样本数量大致相等。用户根据实际需求设置样本数目n_samples、样本特征数目n_features、类别数目n_class、均值mean[]和标准协方差cov等。算法伪代码如算法1所示。 算法1make_gaussian_quantiles算法 Init: (1)输入样本数n_samples、特征数n_features、均值mean[]、标准协方差cov、类别数n_classes; (2)初始化随机数种子myseed; (3)生成n_samples×n_features维符合多维标准正态分布的随机数数据集samples[][]; (4)samples[][]←samples[][]×mean[]+cov; (5)for(每个样本点i)do 计算该样本点序列的方差: endfor (6)对样本集中每个样本的方差进行排序; (7)按照排序后的样本方差找出n_classese-1分位点quantile[]; (8)for(每个样本点i)do 判断该样本点在quantile[]上的区间位置,设置样本标签; endfor end 3.2.2 make_gaussian_quantiles算法并行化 通过分析算法1,可以对需要生成的数据集进行划分,每个进程生成一个符合多维标准正态分布的子数据集,分别计算各自产生的样本方差并进行排序,并按照排序结果分别设置样本标签。假设有N个进程,共需生成n_samples个样本,每个样本有n_features个特征。并行过程如图3所示。 各个从进程生成子数据集并按照样本方差排序,此时,从进程内的样本是局部有序的,本文使用PSRS( Parallel Sorting by Regular Sampling)算法对整个数据集进行全局排序,最后聚集到主进程。 make_gaussian_quantiles算法并行化的具体如下所示: 步骤1主进程设置随机数发生器初始种子,计算出前N个随机数并随机生成高斯簇中心点坐标centerbuffer,然后将其广播到从进程。 步骤2主进程计算各个进程需要生成的样本数。进程i生成的样本数目n_samples_per_procs[i]如式(9)所示: n_samples_per_proc[i]=n_samples/N+left[i], (9) 将式(9)计算得到的n_samples_per_procs[i]分发到从进程。 步骤3从进程随机生成n_samples_per_procsi个符合多维标准正态分布的样本点,然后计算每个样本点到中心点的距离dis[]。 步骤4各个进程按照从小到大的顺序对其生成的每个样本点到中心点的距离进行局部排序。 步骤6此时选取的N个数也是有序的,然后将总共N×N个数聚集到主进程。 步骤7主进程对N×N数据进行排序,此时的数据都是局部有序的,使用归并算法排序可以降低时间复杂度。 步骤8主进程从排序好的N×N个数据中等间隔选取N-1个主元,并将其广播到从进程中。 步骤9从进程根据N-1个主元将dis[]数组划分为N段。 步骤10进程i(i=0,1,2,…,N-1)将第j(j=0,1,2,…,N-1)段发送给进程j,即每个进程都要给其它所有进程发送相应的数据段,并且从其它所有进程中接收数据段,此过程称为全局交换。 步骤11此时,各个进程中的N个数据段都是局部有序的,使用归并算法对其进行最终排序。然后,将排序好的dis[]数组聚集到主进程,就得到了每个样本点到中心点距离的全局排序结果。 步骤12主进程在全局dis[]数组中寻找n_class个分位点quantile[],第j个分位点quantile[j]=j×(n_samples/n_class),j=0,1,2,…,n_class-1。然后将quantile[]广播到从进程。 步骤13从进程依次判断每个样本点到中心点的距离在quantile[]中的区间位置,设置样本标签。各个进程利用shuffle函数打乱样本集的顺序。 并行大数据集生成器[17 - 19]集成了若干并行生成数据集的算法,可以生成分类和聚类数据集、回归数据集、流形学习数据集和因子分解数据集等。用户可以根据自身需求高效地生成GB级数据集。 大数据集生成器的I/O系统的主要功能可以分为2部分:一是提供数据集读、写操作的函数接口;二是实现数据集在各进程之间的分发映射、数据交互等。 (1)多视口并行读取文件。本文在MPI-I/O系统[20 - 22]中实现了多视口并行读取文件的接口。每个进程对应一个文件视口,每个视口拥有独立的文件指针对视口进行读写。一个视口在物理位置上对应原始文件中连续或不连续的部分。文件与视口的关系如图4所示。 Figure 4 File and viewport mapping图4 文件与视口对应图 假设有N个进程,计算出每个进程需要读取的文件大小:bufsize=filesize/N。首先,使用MPI_FILE_OPEN并行打开文件;然后,根据每个进程的编号设置各进程的文件视口,通过调用MPI_FILE_SEEK将每个视口的文件指针移动到特定位置;最后,使用MPI_FILE_READ以阻塞方式将各个文件视口中的数据读入该节点的内存buffer中,并调用MPI_FILE_CLOSE关闭文件。 (2)共享指针写入文件。共享文件内有且仅有一个文件指针,任何一个进程对文件进行读写操作都会影响其他进程。共享文件的写入过程如图5所示。 Figure 5 Schematic diagram of writing shared files图5 共享文件写入示意图 假设有N个进程,首先,使用MPI_FILE_OPEN并行打开文件,调用MPI_FILE_WRITE_ORDERED使同一进程组内的所有进程以共享文件指针的方式按顺序写入数据;然后,根据各个进程的rankID标识,第0,1,…,N-1号进程依次对文件进行写入,当一个进程写入后,文件指针自动指向下一个数据单元,每个进程都向共同的文件视口中写入存放在各自buffer中的数据;最后,调用MPI_FILE_CLOSE接口关闭文件。 本文还提供了数据集分发、映射的接口。由主进程将文件读取到自己的缓冲区dataBuffer内,设置映射规则将文件分块发送到所有其他进程。假设将数据集分发到N个进程,数据集中共包含datasize个样本,各进程接收的样本数n_samples_per_proc[i]如式(10)所示: n_samples_per_proc[i]=datasize/N+left[i], (10) 文件到各进程的映射规则为连续分块放置,即每个进程接收文件中某一块连续数据,如图6所示。 已知某样本在原始文件中的全局索引globalIndex,根据文件块映射规则,需要寻找该样本点在并行节点上的位置,即获取样本点所在的进程号sendID和局部索引localIndex。首先,根据n_samples_per_proc[]数组计算出从进程0开始的累积样本数目accum_local_array[](数组元素升序排列)。然后,循环比较找到globalIndex应该插入accum_local_array[]中的位置下标,该下标即为样本点所在进程号sendID。样本点在sendID号进程的局部索引为:localIndex=globalIndex-accum_loaca_array[sendID-1]。为获取样本点,本文使用了MPI_Send和MPI_Recv接口以阻塞方式实现点对点通信。由进程sendID分别发送样本点的特征和标签,进程recvID接收数据。 为了验证并行大数据集的生成器对数据集生成速度和规模的有效提高,在天河二号计算机上进行测试,GPU(V100)集群中每个计算结点包含 2 个 Intel(R) Xeon(R) Gold 6132 、14核心的多核中央处理器(CPU)和 4 个 GPU 卡。每个计算结点拥有 256 GB 内存(2 个 CPU 共用)。GPU(V100)集群操作系统为 Red Hat 7.3。MPI编译环境为mvapich2/2.3rc2-gcc-4.8.5-CUDA-9.2.88。 为了测试人工数据集[23,24]是否满足大数据处理分析算法的测试需求,本文将MPI并行生成的数据集通过I/O系统的并行接口以.csv格式输出到同一个文件,然后调用并行大数据处理分析算法对生成的不同用途的数据集进行测试。以下测试过程中均使用原始生成的数据集,并未对其进行数据预处理。 (1)单标签聚类:make_blob数据集和make_gaussian_quantiles数据集,使用dbscan和GaussianNB算法进行功能验证; (2)双向聚类:make_biclusters数据集和make_checkerboard数据集,使用Spectral Biclustering算法进行功能验证; (3)单标签分类:make_circles数据集和make_moons数据集,使用dbscan和k-means算法进行功能验证; (4)多标签分类:make_multilabel_classification数据集,通过PCA (Principal Component Analysis)和CCA (Canonical Correlation Analysis)对数据集进行分析,抽取了数据集的前2个主成分进行分类,然后使用sklearn.multiclass.OneVsRestClassifier中带有线性核的C-SVC(Support Vector Classification) 的分类器学习每个类的判别模型。 (5)回归:make_regression数据集,使用随机抽样一致性算法RANSAC(RANdom SAmple Consensus)和线性回归算法LINEAR(LINEAR regression)进行功能验证; (6)流形学习:make_swiss_roll数据集和make_s_curve数据集,使用ISOMAP(ISOmetric MAPping)、 LLE(Locally Linear Embedding)、LE(Laplacian Eigenmaps)、LTSA (Local Tangent Space Alignment)和SE(Spline Embedding)等算法对数据集进行降维。 不同用途数据集的功能验证测试结果如图7所示。由图7可以看出,并行大数据集生成器生成的不同用途的数据集可以满足大数据处理分析算法的性能测试需求,可以用来作为基准测试数据集[25 - 29],其功能性得到了验证。 Figure 7 Functional verification of different datasets图7 不同数据集的功能验证 为了展示数据集生成器的数据生成速度以及不同数据集生成算法的生成速度是否一致,本文从中选取了5个有代表性的数据集生成器,测试了它们在20,50,100,200,500,1 000个进程下生成1e8个样本的程序运行时间,结果如图8所示。 Figure 8 Running time of different algorithms with different numbers of processes图8 不同算法在不同进程数目下的运行时间 从图8可以看出,随着进程数目的不断增加,各类数据集生成算法的运行时间不断缩短,符合预期效果。尽管不同算法的时间复杂度和并行设计不尽相同,但是它们生成数据集的速度是相对一致的。随着进程数目的不断增加,各类算法运行时间的差距不断减小。在1 000个进程下并行执行时,各类算法的运行时间基本相同。 为了测试算法并行后的性能,本文设置样本规模分别为106,107,108,109,测试算法在1,20,50,100,200,500,1 000个进程并行工作时的执行时间。主要的评估指标为加速比和效率,加速比用于评估并行算法的执行速度,效率用于度量各进程的资源利用率。并行程序的效率计算公式如式(11)所示: (11) 限于篇幅,本文只给出生成make_regression数据集算法的加速比和效率示意图(其他数据集算法的评测与make_regression类似),如图9和图10所示。 Figure 9 Speedup of make_regression algorithm after parallelling图9 make_regression算法并行加速比 Figure 10 Efficiency of make_regression algorithm after parallelling 图10 make_regression算法并行效率 由图9可以看出,当样本规模比较大时,随着分配进程数目(1 000以内)的增加,算法的加速比不断增大,但是增加的速度越来越慢;当样本规模较小时,随着进程数目(1 000以内)的增加,算法加速比先增加后减小。当进程数目不变时,样本规模越大,算法加速比越高。这说明多进程并行带来的算法加速效果是有局限性的,这不仅取决于算法的并行部分占整个算法的比例,而且还取决于各进程之间的通信开销。样本规模较小时,各进程的任务量也很小,进程间通信所消耗的时间抵消了一部分并行计算节省的时间,极端情况下,甚至会出现加速比小于1的情况,此时,参与并行计算的进程越多,算法的运行速度越慢。 由图10可知,样本规模一定时,随着进程数目的增加,算法效率不断降低,且降低的速率越来越慢;进程数目一定时,随着样本规模的增加,算法效率不断提高。效率主要用于度量各进程的资源利用率。任务量一定,进程数目越多,平均每个进程的利用率就越低;进程数目一定时,算法任务量越大,每个进程的资源利用率越高。在样本规模达到1e9时,在1 000个进程下运行并行程序,效率可达到80%以上。 本文面向超级计算机实现了一个大数据集生成器,主要用于解决大数据处理分析算法中的数据集体量不足问题,帮助测试大数据分析算法性能。在并行生成各种复杂分布随机数的基础上,利用MPI并行编程技术设计实现多种数据集(如单标签聚类数据集、分类数据集、回归数据集、流形学习数据集、因子分解数据集)的并行生成算法,以生成GB级数据。为大数据处理分析算法设置数据集在不同进程间的分发、映射规则,利用点对点通信实现不同节点上的数据交互访问功能。基本实现了大数据集从产生、读写、分发、映射再到样本点索引的全过程。2.3 复杂分布随机数的生成
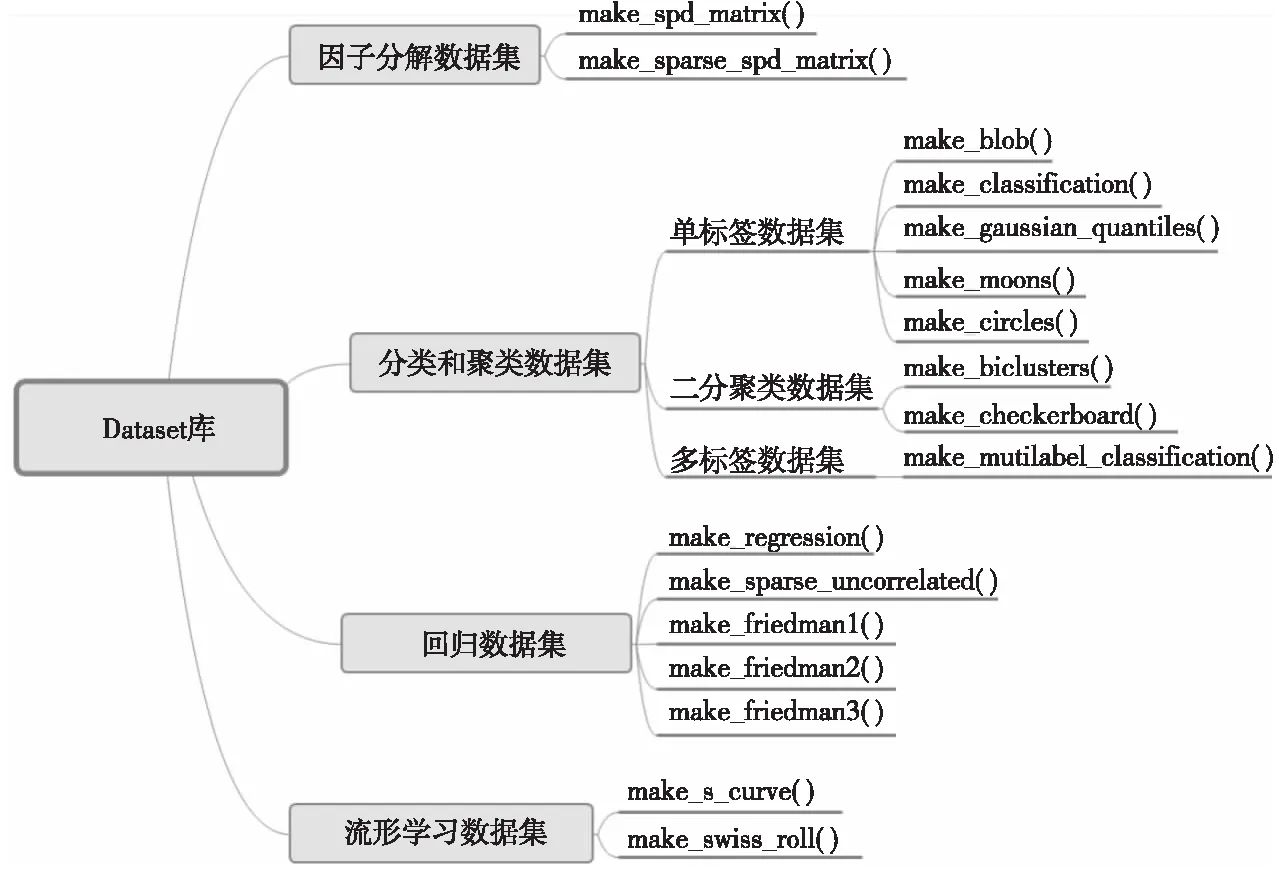
3 并行大数据集生成器的构造
3.1 线性同余算法并行设计
3.2 人工大数据集生成算法并行设计
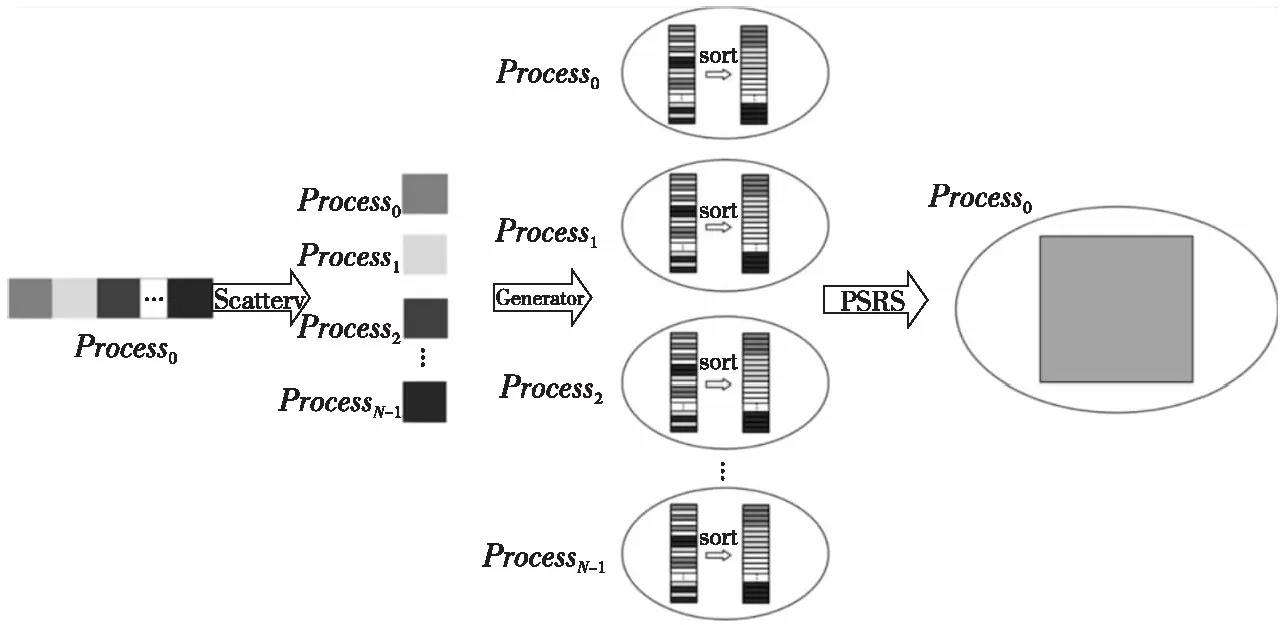

4 I/O系统
4.1 MPI-I/O并行读写文件


4.2 数据集分发映射
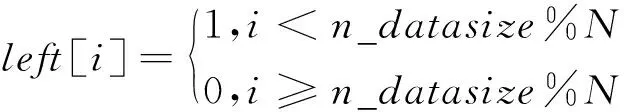
5 实验与评估
5.1 实验环境
5.2 数据集功能测试

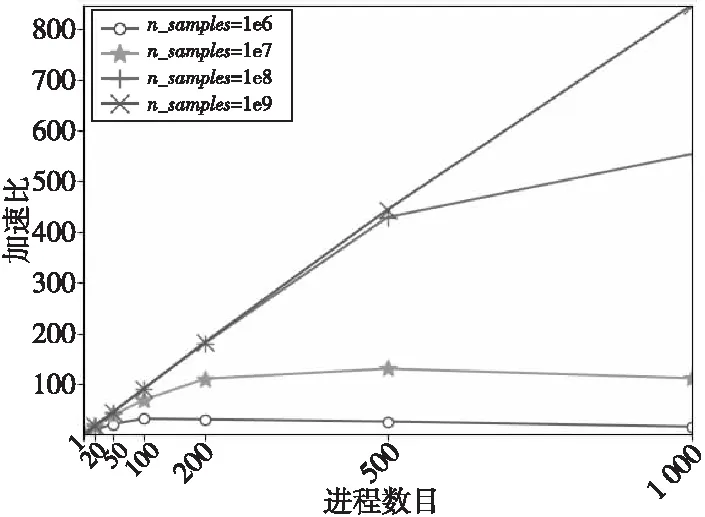
5.3 算法性能分析



6 结束语
