基于广义总场散射场技术的地面电磁环境数值方法

杨 超， 任泽平， 乔海亮， 陈剑楠

(西北核技术研究所， 西安 710024)

研究电磁波与地面的相互作用在遥感、移动通信、目标识别和军事等领域有重要的意义[1-2]。基于时域微分方程的时域有限差分(finite-difference time-domain, FDTD)方法是解决电波传播与电磁散射的常用工具[3-7]，它是由Yee[8]于1966年通过直接对时域Maxwell方程进行差分离散而提出的，不仅可求解时谐连续波的散射，还可计算非时谐脉冲波的散射。用FDTD方法计算散射问题时，通常将计算区域划分为总场区和散射场区，通过传统总场散射场(total-field/scattered-field, TF/SF)方法能有效引入平面入射波，但散射体被限制在TF/SF边界内[9-10]。随后，众多学者对TF/SF进行了改进[5,11-17]。

FDTD方法是研究电磁波与地面相互作用的常用数值计算方法[18-25]，而有效的平面波加载方法一直是重点关注的研究内容。Chan等[18]最先提出将FDTD方法应用于粗糙地面的散射计算。1994年，Fung等[19]较系统地阐述了用FDTD方法研究粗糙地面的电磁散射，提出以上表面处的TF/SF边界为粗糙地面来加载入射波，侧边直接接吸收边界，此时TF/SF不再是一个闭合的空间，而退化为一个面。该方法是用有限面元激励源代替平面入射波，无法将真实入射波引入到总场区中。Wong等[21]用三波法计算无限大半空间平面的散射特性，三波法是一种典型的半解析半数值混合方法，需解析计算出各个区域场分量，很难推广到粗糙地面及多层媒介情形。Winton等[22]提出了双侧边垂直加入法，采用非闭合TF/SF边界，通过在左右两边的TF/SF边界处附加1维FDTD的方法来引入入射波。

有文献用广义总场散射场(generalized TF/SF， G-TF/SF)方法模拟计算了无限大楔形物体的电磁波散射[26-27]，四周采用Berenger完全匹配层(perfectly matched layer, PML)[28]吸收边界，减少了截断处的绕射现象。本文将G-TF/SF方法应用于地面的电磁散射，四周改用吸收效果更好的卷积PML(convolutional PML, CPML)[29]吸收边界，可减小计算过程中由地面四周截断产生的边缘效应。与TF/SF方法类似，G-TF/SF方法在总场边界处加上或减去入射场，由于G-TF/SF部分边界埋在PML层中，所以在传统TF/SF的基础上，需对埋在PML层中的G-TF/SF边界入射波乘以相应的系数，以保证将入射波等效到主网格区域进行计算。为验证G-TF/SF方法的正确性，本文模拟计算了自由空间电磁波传播和水平有耗地面的电磁特性，计算结果表明，G-TF/SF方法可高精度地模拟水平地面对电磁波的散射作用，为后续将G-TF/SF方法应用于真实粗糙地面及分层媒介的电磁环境计算提供了理论依据。

1 基于FDTD的G-TF/SF方法

1.1 CPML区域G-TF/SF边界的递推公式

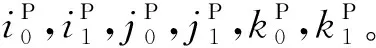
图2为G-TF/SF边界的6个面。G-TF/SF边界的侧面及底面均处于CPML区域，上面(图2(e))的V区域位于自由空间，其余也均位于CPML区域。G-TF/SF边界将FDTD计算区域划分为总场区和散射场区，G-TF/SF边界内(含G-TF/SF边界)的区域包含入射场和散射场，G-TF/SF边界外部只有散射场。自由空间中的G-TF/SF边界处理方法与传统的TF/SF边界完全相同[6-7]，而在CPML区域的G-TF/SF方法则需进行特殊处理。

对电场和磁场进行空间与时间离散[7]，CPML区域电场Ex的FDTD离散迭代公式为[6-7]

(1)

(2)

(3)

(4)

(5)

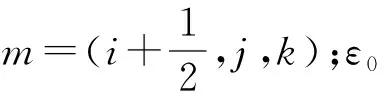
与TF/SF引入入射波类似，G-TF/SF边界法向分量的FDTD计算公式不变，切向分量的计算公式需改变。CPML区域中j=j0面(图2(c))G-TF/SF界面切向场Ex的离散迭代公式为

(6)

(7)

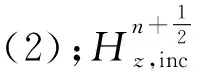
1.2 CPML层G-TF/SF边界入射场计算

在进行FDTD计算前，需进行预处理，求解CPML区域所需的入射场，令

Ψinc=X0ACPML(θinc，φinc)

(8)

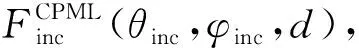
对于给定的入射角，需确定CPML区域中G-TF/SF界面位置是入射波的起源或到达区域，对于入射到CPML处的电磁波，ACPML(θinc，φinc)为衰减因子ηatt

(9)

对于起源于CPML区域的电磁波，ACPML(θinc，φinc)为增益因子ηamp

(10)

通过FDTD预处理可计算得到在w方向CPML层的ηw,att(θinc，φinc,d)和ηw,amp(θInc，φinc,d)。因为只用一侧TF/SF边界，存在着场泄露和两侧边界反射的问题，为减少偏差，在预处理中取CPML层最中间的电磁场幅值来计算ACPML。

CPML层所有G-TF/SF边界的ACPML都可通过ηw,att和ηw,amp计算。以图2(a)的i=i0面为例，对于90°<θinc≤180°，

区域Ⅰ：

ACPML=Ax,CPML(i0)Ay,CPML(j)

(11)

区域Ⅱ：

ACPML=Ax,CPML(i0)

(12)

区域Ⅲ：

ACPML=Ax,CPML(i0)Ay,CPML(j)

(13)

区域Ⅵ：

ACPML=Ax,CPML(i0)Ay,CPML(j)Az,CPML(k)

(14)

区域Ⅴ：

ACPML=Ax,CPML(i0)Az,CPML(k)

(15)

区域Ⅵ：

ACPML=Ax,CPML(i0)Ay,CPML(j)Az,CPML(k)

(16)

类似地，可计算i=i1，j=j0，j=j1，k=k0，k=k1面的ACPML值。利用式(8)-式(16)可得到CPML层所需的入射电场和磁场，进而可在CPML层G-TF/SF边界上进行电场与磁场迭代。

2 算例比对与结果验证

入射平面波为时谐波E(t)=sin(2πft)，频率f=300 MHz，波长λ=1 m，入射波方向为负z方向，电磁极化方向为x方向，FDTD空间离散间隔为λ/40=0.025 m。

2.1 自由空间

为在整个3D空间验证G-TF/SF的正确性， 利用G-TF/SF和TB方法计算了自由空间z=0面上的电场幅值，如图5所示。由图5可见，G-TF/SF方法计算z=0平面的幅值范围与理论值1 V·m-1的最大相对偏差为0.8%，而TB方法与理论值相差较大。

利用G-TF/SF和TB方法计算了自由空间y=0面上的电场幅值，如图6所示。由图6可见，G-TF/SF方法计算结果与理论值符合很好，而TB方法与理论值相差较大。TB方法无法高精度地将入射场引入计算区域，而G-TF/SF可高精度地引入入射波。

2.2 有耗地面

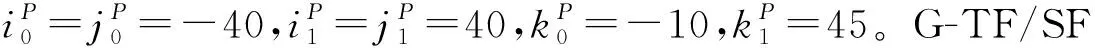
图7为利用G-TF/SF、TB和解析方法[30]计算的有耗地面上Ex(0,0,10)时域波形。由图7可见，G-TF/SF方法与解析方法计算结果的波形吻合很好，而TB方法存在较大偏差。

图8为利用G-TF/SF、TB与解析方法计算不同高度处电场幅值，G-TF/SF和TB方法计算结果为不同离散点(0,0,k)处，Ex(0,0,k)的电场幅值。由于入射波与地面的反射波传播方向相反，频率相同，所以电场沿不同高度的分布应为驻波形式。

由图8可见，G-TF/SF方法计算结果与解析法吻合很好，电场沿不同高度的分布为驻波形式，而TB方法存在很大偏差。

图9为利用G-TF/SF和TB方法计算有耗地面上y=0面的电场幅值。由于是水平地表，电场幅值与x方向无关，G-TF/SF方法计算结果与理论值一致。电场幅值沿z方向的变化即为图8所示曲线，TB方法计算结果存在较大偏差。

图10为利用G-TF/SF和TB方法计算有耗地面上z=0.25 m(即k=10)面上的电场幅值。由图10可见，G-TF/SF方法的计算结果在1.51～1.513 V·m-1范围内，与理论值符合很好，而TB方法与理论值相差较大。

3 结论

本文将G-TF/SF方法应用于地面的电磁环境计算，四周采用CPML吸收边界，减小了计算过程中由于地面四周截断产生的边缘效应。与传统TF/SF方法一样，G-TF/SF方法在总场边界处加上或减去入射场，但G-TF/SF方法把部分总场边界埋在CPML层中，在传统总场边界条件的基础上，需对埋在CPML层G-TF/SF边界入射波值乘以相应的系数，保证入射波等效到主网格区域进行计算。相应的系数可通过FDTD预处理计算不同CPML深度处的衰减值而得到。

本文用G-TF/SF方法模拟计算了自由空间电磁波传播及水平有耗地面上的电磁特性。结果表明，G-TF/SF可高精度地对自由空间的电磁波传播及水平有耗地面电磁环境进行数值模拟计算，验证了G-TF/SF方法的可靠性，与TB方法相比，展现了G-TF/SF方法的优越性。本文的相关研究可为后续将G-TF/SF应用于真实粗糙地面及分层媒介的电磁环境计算提供理论依据和技术支撑。