触土推板对土壤动态接触行为的离散元分析

2022-08-11马小英杜伊健闫玉涛邵鸿媚

沈阳理工大学学报 2022年3期

马小英，杜伊健，闫玉涛，邵鸿媚

(1.沈阳理工大学 a.机械工程学院；b.环境与化学工程学院，沈阳 110159；2.东北大学机械工程与自动化学院，沈阳 110819)

土壤在受到外力作用时产生的动态行为变化通常与作用力系统、工况环境条件及土壤性质相关，曾德超[1]以吉尔与范登堡的分类为基础，给出了土壤行为的定义，对土壤行为的动态变化过程、机理及影响因素进行了分析；但这种基于连续介质理论的土壤力学模型难以应对复杂的土壤变化。

随着计算机技术和数值模拟技术的的发展，一种基于不连续数值模型的离散元理论被提出，离散单元法(Discrete Element Method，DEM)[2]常用来描述复杂的散体系统变化，为解决动态响应问题提供了新的思路。Ucgul M等[3]采用离散单元法对土壤-板型犁的相互作用进行了模拟，验证了离散单元法对预测相互作用模型的有效性。Wang X等[4]利用离散单元法开发模型，研究了不同模型颗粒半径对土壤的破裂距离、扰动面积、密度变化率等参数的影响。王鹏等[5]利用离散单元法研究了铲式成穴器在不同倾角下的工作过程，确定了成穴器倾角对穴孔长度变化与宽度变化的影响。

推土板是一种与土壤发生接触响应的触土部件，常用于平整土地，推集泥土等作业，可针对各类散体颗粒进行工作。刘国敏等[6]对不同表面形态的推土板作用下的土壤变化规律和影响因素进行了离散元模拟，解释了推土板表面形态对土壤动态行为的影响。郭志军等[7]对推土板的触土曲面进行了不同的触土曲面准线设计，确定了不同曲面对工作阻力的影响程度，为推土板的结构优化提供了新参考。

国内外针对推土板的的研究多偏向表面形态、曲线设计等外形结构，针对推土板折弯角度对推土板性能影响的研究极少，因此对触土推板折弯角度的研究很有必要。本文研究推土板在不同折弯角度下与土壤产生动态接触行为时土壤的动态响应特性，以离散单元法作为研究手段，对触土件与土壤颗粒进行接触分析；利用离散单元法分析不同折弯角度的触土推板工作压力的变化趋势、研究触土推板与土壤颗粒相互作用时的变化规律，确定触土推板在推土作业中最佳折弯角度，并为后续的优化分析提供理论支撑。

1 触土推板模型建立

1.1 模型参数

触土推板模型的参数包括长度、宽度、高度、厚度、质量、角度等。触土件与土壤接触时会对土壤颗粒产生动态响应变化，其中角度参数对土壤的动态影响不明朗，因此针对一种具有折弯角度的平面型触土推板进行分析，模型材料选用45号碳素结构钢。触土推板模型如图1所示。

图1 触土推板模型

触土推板模型的左侧端点为模型末端，右侧端点为模型始端，模型的设计将整板分为A和B两段，两段长度分别为l1=62.1mm和l2=80mm，两段的尺寸比接近3∶4。模型的水平方向尺寸为L1，竖直方向尺寸为L2，两段之间的折弯角度为α，工作时的切土角度为β。其中：

L1=l1+l2×cosα

(1)

L2=l2×cosβ

(2)

α+β=90°

(3)

触土推板的折弯角度α一般为0～90°范围内，当折弯角度大于45°时，B段竖直方向的尺寸分量大于B段水平方向的尺寸分量，在固定质量参数条件下竖直方向上过多的尺寸分量会影响触土推板的推土能力，造成材料的浪费，因此将最大折弯角度设定为45°。

触土推板前端土壤的堆积、波动等动态行为变化直接受切土角β大小的影响[8]，为确定触土推板最优折弯角度，将折弯角度确定为5个等级，模型整体参数如表1所示。尺寸参数变化如图2所示。

表1 模型尺寸参数表

图2 模型尺寸参数变化趋势

随折弯角度的增加，L1方向尺寸减小速度逐渐增大，此时，触土推板在水平方向的作用范围缩小的也更快。

1.2 模型运动分析

触土推板的工作状态为水平直线运动，在水平进给工作时将土壤散体颗粒推离原始位置。对触土推板运动过程中两段板上的两颗粒进行分析，其受力和运动状态如图3所示。

图3 触土推板工作状态下颗粒运动趋势

在不考虑颗粒间作用力及运动碰撞等情况时，A段的颗粒受到Fa方向的力，B段的颗粒受到来自Fb方向的力。若A段位置γ角度为0°，B段位置φ角度为90°，模型拥有理想的工作状态。

但在实际运动状态中，触土推板由于加工误差、安装误差、振动、颗粒形状等因素的影响，推板并不能以理想的运动状态运动。

单个土壤颗粒的运动方向存在不确定性，在多颗粒同时运动时，需要考虑更多的影响因素，包括土壤颗粒间的接触力、摩擦力、粘性力、范德华力、液桥力等多种作用力。为在更复杂的工况环境下进行分析，需要使用离散单元法。

2 土壤力学离散单元模型

2.1 离散单元法颗粒模型原理

离散单元法是把离散体看做具有一定形状和质量的离散颗粒单元的集合。根据几何特征可将离散体单元分为颗粒和块体，土壤属于一种散体颗粒，在对土壤颗粒进行分析时常采用颗粒离散单元法。一般情况下认为颗粒的运动是相互独立的，只有在发生相互接触时才会在接触点处产生力的相互作用，因此颗粒会表现出离散性，离散性使颗粒在受载和不受载的情形下产生复杂且不同的运动。

离散单元法的颗粒模型是将颗粒与颗粒、颗粒与边界的接触采用振动运动方程进行模拟，模拟过程如图4所示[9]。

图4 接触模型转换成振动模型原理图

图4中，P1和P2为两个颗粒；R1和R2分别为颗粒的接触半径；δ为接触变形量；μn为法向接触相对位移；μ为滑动位移；Kn、Ks为接触模型中的法向和切向弹性系数；ηn、ηs分别为接触模型中的法向和切向粘滞阻尼系数；2a为接触圆直径。颗粒接触模型可表示成振动模型，振动模型由法向振动模型、切向振动模型和滑动模型组合构成。

2.2 土壤模型建立

土壤颗粒形状不规则且性质迥异，采样地不同，其性质参数会有很大不同；不同材质和成分的土壤具有不同的物理参数，且在相互作用中的接触参数也会不同，进而影响实际的动态接触响应效果。土壤颗粒的力学参数难以直接测量，精确的模拟结果取决于土壤颗粒模型参数的设置和标定，合理的土壤模型能够准确地反应土壤的力学性质[10]。

在土壤模型中将颗粒半径设置为4mm，土壤颗粒的粒径分布呈正态分布。采用Hertz-Mindlin无滑动接触模型模拟颗粒与颗粒、颗粒与触土推板间的接触行为。离散元分析过程需要确定恢复系数、摩擦系数、密度、剪切模量、泊松比等参数，离散元软件EDEM参数设置如表2所示，土壤为来自吉林省松原市长岭县腰井子牧场的砂壤土，经参数标定获得相关参数[11]。

表2 EDEM模拟参数设置

3 触土推板流动性分析

触土推板在推土作业时，当土壤颗粒与推板接触时颗粒发生移动，B段斜板位置处的颗粒会出现向A段平板方向运动的趋势；由于推板平动作业时颗粒运动趋势不明显，因此建立流动颗粒-静物流动性分析模型。通过在EDEM中建立边界完成颗粒堆积，将触土推板模型放入计算域内作固定设置，挡板抽离后，颗粒在重力作用下自然下落并与推板发生碰撞接触，经由推板的阻挡逸出边界，完成自由状态下不同折弯角度推板的颗粒流动性分析。流动性分析模型如图5所示。

图5 流动性分析模型

分析模型的总时间为3s，阶段分析步设置为15%，网格单元设置为2.5R(R为颗粒半径)，土壤颗粒由上向下共生成25000个；当模型分析时间为1s时，中间部分的挡板抽离，静止的颗粒开始做自由落体运动，在运动一段时间后开始进行流动性分析。五种折弯角度的推板分析过程中的运动速度变化如图6所示。

图6 土壤颗粒速度曲线图

颗粒在1～3s的时间内开始流动，因此只针对1s后的数据进行分析，并将时间轴坐标归零处理。由图6可以看出，颗粒掉落，并在0.2s左右达到速度峰值，此时颗粒与触土推板接触，速度开始下降，减速的颗粒与逐渐加速的颗粒碰撞冲击造成速度波动，当颗粒通过模型的缺口时开始逸出，避免造成堆积。随着时间的增加，颗粒的速度由波动变为稳定下降，45°的触土推板速度峰值最高，分析结束时的速度最低，说明45°推板的颗粒流动性更好，角度越大，流动性越好。15°触土推板在速度波动周期内的整体数值较低，且分析结束时的速度数值最大，说明推板在这种角度下对土壤颗粒的流动性控制更稳定。颗粒数目的变化曲线如图7所示。

图7 颗粒数目变化曲线图

由图7 可以看出，颗粒的数量变化曲线与速度变化曲线趋势相同，颗粒的数目随时间的增加而稳定下降，但折弯角度不同，颗粒数目的下降速率不同，分析时间周期内最终留存的颗粒数目也不同。

图7中，5°推板与15°推板的留存颗粒数目相近，说明两推板对颗粒数目的作用效果相近。综合两种曲线分析，15°推板的颗粒数目变化呈线性趋势，且留存颗粒数目更多，对于实现推土作业的触土推板而言，这种综合性能十分理想。颗粒的运动状态如图8所示。

图8 颗粒运动状态图

由图8可以看出，颗粒的整体状态可划分为三个区域：上端颗粒流动区、中端颗粒扰动区、下端颗粒微动区，三个区域很好地反映了颗粒的运动变化状态。

综合分析认为触土推板的折弯角度为15°时，土壤颗粒的流动性更好，颗粒数量留存率更高。

4 土壤颗粒动态变化离散元分析

触土推板的流动性分析仅表示土壤颗粒在与推板接触时的运动状态，并不能反映土壤颗粒在与推板发生动态接触时的动态响应变化，因此需要采用土槽实验进行分析。利用EDEM软件生成一个长300mm、宽300mm、高200mm的土槽放置土壤颗粒。土壤颗粒动态变化分析模型如图9所示。

图9 土壤颗粒动态变化分析图

为确定推板在工作时不同层级颗粒的运动变化，在生成颗粒时将土壤层按深度自下而上分为5层，每层颗粒生成6750个，共生成33750个颗粒。设定推板的前进速度为0.05m/s，分析时间步为20%，网格尺寸为2.5R，模型分析时间为5s。仅针对2～5s时间范围内触土推板运动阶段进行分析，并将此时的时间坐标归零。

不同工作状态的最终作用效果不同，为测定满负载状态下推板模型的工作压力与颗粒层动态变化，将土壤层高度设置为高于推板高度，土壤层延伸至无限远，使用土槽壁模拟运动阻碍，测定颗粒层的动态变化，如图10所示。

图10 土壤层动态变化图

由图10可以看出，触土推板向左移动，逐渐对土壤层颗粒进行挤压，颗粒层受力升高呈现出层级弧形空间堆积的效果，左上方颗粒层升高越过推板至推板后方，右下方颗粒层仅在触土推板的破坏范围内呈现出层级破坏效果，但原有的土壤层堆积形式依旧保持初始状态。为直观地呈现出土壤层动态变化，采用图11所示的势能曲线图进行表示。

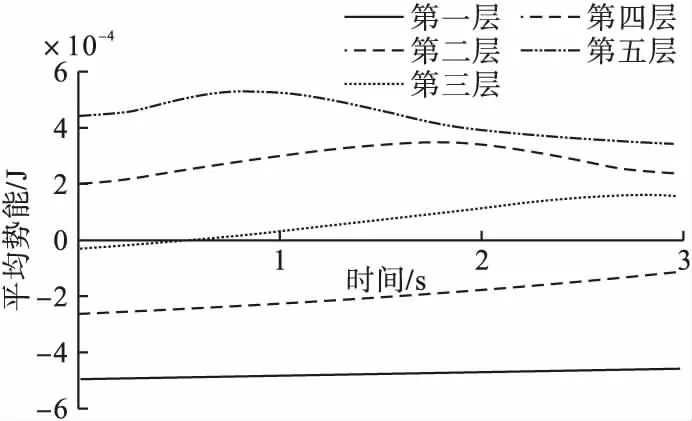
图11 土壤颗粒势能变化趋势图

由图11可以看出，一～三层颗粒在工作时，势能随触土推板的挤压而升高；随着时间变化，第四层与第五层的颗粒出现势能先升高后降低的效果，但第五层的势能变化波动与第四层比出现更早。更早的势能变化说明颗粒越过触土推板的时间更早。

对具有不同折弯角度的触土推板，前三层基本呈现出折弯角度越小，颗粒势能的升高越明显的现象。第三层土壤颗粒在2.8s出现势能下降的趋势，此时颗粒越过了推板。触土推板的压力变化曲线如图12所示。

图12 触土推板压力变化曲线图

由图12可以看出，触土推板在作业时，受到的压力随时间增加而增大，并且折弯角度越大，提升至峰值的速率越慢。推板在稳定前进时受到的压力随时间产生波动，5°推板的压力变化十分显著，具有组别中最高的峰值数据；15°推板的压力变化较稳定；25°推板的变化较大，并且在分析周期末端产生了剧烈的变化；其余两条曲线压力较小，但变化较剧烈。

综合分析结果，当触土推板折弯角度为15°时，推板压力变化较稳定，且此时触土推板的工作范围更大，工作效率更高。