一种改进的自适应噪声抵消系统算法研究

伍彩云，翁晶晶

(沈阳理工大学 装备工程学院，沈阳110159)

在噪声控制中，自适应噪声抵消系统在外部干扰源特性未知、传递途径不断变化以及待测对象和背景噪声波形相近的情况下，能够有效地消除外界噪声信号的干扰，从而提高信噪比[1]。传统最小均方(Least Mean Square，LMS)算法是目前最基础的自适应滤波算法，其结构简单，易于实现，应用广泛。算法的步长因子为定值，需要人为提前设定其大小。步长因子取值小，稳态误差小，但收敛速度差；步长因子取值大，收敛速度好，但稳态误差大[2-4]。鉴于此，国内外学者提出了多种变步长 LMS 算法。各学者通过不同的函数形式建立误差信号与步长因子间的特定关系，使变步长LMS算法在收敛初期有较大的步长因子，以得到较快的收敛速度；在要进入稳态阶段时，步长因子减少至较小值，获得更好的稳态性能。文献[5]基于Sigmoid函数提出了变步长最小均方(Sigmoid Variable Step Least Mean Square，SVSLMS)算法，相比传统的LMS算法，其收敛速度更快，但在完成收敛阶段时，步长因子值仍较大，导致稳态误差较大，稳定性能差。文献[6]针对文献[5]的缺点，给出了改进的SVSLMS算法，该算法将步长因子和误差信号构造为非线性函数关系，其在收敛速度和抗噪性能方面得到了提升，且具有偏小的稳态误差。除此之外，针对步长因子的其他函数形式，文献[7]提出了基于t分布的变步长(Based on Various T-distribution Least Mean Square，BVTLMS)算法，该算法在t分布概率密度函数的基础上对步长因子进行调整，实验结果表明，在收敛速度和抗噪性能上，BVTLMS算法都有大幅度提升，但步长因子函数复杂，占用较多存储空间。

现有的变步长LMS算法在一定程度上解决了收敛速度和稳态误差间的矛盾，为进一步提升算法性能，本文提出了一种新的基于Softsign函数的变步长LMS算法，该算法采用新Softsign函数对步长因子进行调整，并加入了绝对估计误差的扰动量，使权向量更新后始终保持在最优值。同时设计了一款自适应噪声抵消系统仿真平台，该平台具有噪声叠加、去噪处理等功能，操作界面友好。利用该仿真平台对传统LMS算法、已有变步长LMS算法和本文提出算法的噪声抵消特性进行了对比实验。

1 自适应噪声抵消系统

图1所示为自适应噪声抵消系统的原理图。

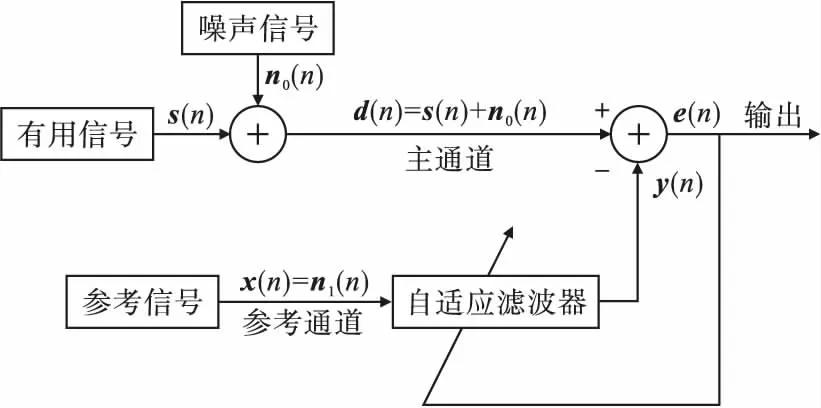
图1 自适应噪声抵消系统原理图

图1中，主通道的n时刻含噪信号d(n)包括有用信号s(n)与噪声信号n0(n)，参考信号x(n)是与噪声信号相关的参考通道输入信号，该信号经过自适应滤波器后得到输出信号y(n)与主通道的含噪信号相抵消，此时误差信号e(n)变为有用信号s(n)，从而达到去噪的效果[8]。

2 自适应滤波算法设计

2.1 LMS算法

传统LMS算法属于随机梯度算法，基本思想是在运算过程中沿滤波权系数的负梯度方向搜索至其最优值，即期望信号和输出信号间的均方误差(Mean Square Error，MSE)达到最小。自适应滤波器基本原理如图2所示[9]。

图2 自适应滤波器基本原理

图2中a(n)为n时刻滤波器的输入信号；v(n)为干扰信号；f(n)为期望信号；y(n)为输出信号；e(n)为误差信号。

LMS算法的迭代算式为

y(n)=wT(n)a(n)

(1)

e(n)=f(n)-y(n)

(2)

w(n+1)=w(n)+2μa(n)e(n)

(3)

0<μ<1/λmax

(4)

式中：w(n)为n时刻滤波器的权向量；μ为控制算法性能的重要参量，称为步长因子，其收敛条件为式(4)；λmax是输入信号自相关矩阵的最大特征值。

由上述迭代算法可知，LMS算法在步长因子的选择中不断显现出收敛速度和稳态误差间不协调的问题。

2.2 Softsign函数的新变步长LMS算法

为解决LMS算法存在的收敛速度和稳态误差间不协调的问题，在保证算法性能的前提下，采用新Softsign函数建立步长因子μ′(n)与误差信号e(n)间的函数关系。

Softsign函数具有反比例中心对称，能够微分、去中心等特点，返回值介于-1和1之间，其计算表达式为

(5)

式中：y为函数的因变量；x为函数的自变量。

将标准Softsign函数经过求导、自变量取倒数以及向上平移1个单位的方式，得到新Softsign 函数表达式为

(6)

现用μ′(n)和e(n)分别代替y和x，得到步长因子μ′(n)和误差信号e(n)间的新函数关系为

(7)

式(7)对应的函数关系如图3所示。

图3 μ′(n)和e(n)的函数关系

分析式(7)和图3可知，在算法收敛初始阶段(误差信号较大)，步长因子的调整函数可保持较大的步长因子值，从而提高算法的收敛速度。在收敛完成阶段(误差信号趋近于零)，步长因子的调整函数可选择较小的步长因子值，从而提高算法的稳定性能。

2.2.1 参数对步长因子的影响分析

为提高本文算法的可控性，在式(7)中加入参数α>0、β>0，得到步长因子μ(n)和误差信号e(n)间的新函数表达式为

(8)

式中：α用于保持函数形状；β用于限定函数的取值范围。

利用步长因子μ′(n)和误差信号e(n)间的关系曲线定性分析引入的参数α、β对算法性能的影响如下。

(1)参数α对算法性能的影响

选择β=1，α分别取值为2、3、4，得到μ′(n)与e(n)的关系曲线如图4所示。

图4 μ′(n)与e(n)的关系曲线(β=1，α不同)

由图4可见，对于同一初始误差，当α越大时，算法在收敛初期提供的步长因子值越大，但算法在完成收敛阶段的稳定性能下降。当α越小时，算法在完成收敛阶段的稳定性能越好，但算法的收敛速度较慢。

(2)参数β对算法性能的影响

选择α=3，β分别取值为0.9、1、1.1，得到μ′(n)与e(n)的关系曲线如图5所示。

图5 μ′(n)与e(n)的关系曲线(α=3，β不同)

由图5可见，对于同一初始误差，β值越大，在初始收敛阶段，算法的收敛速度越快。但β值过大，会导致步长因子不满足式(4)的收敛条件，算法发散。当β取值过小时，步长因子μ′(n)的迭代变化区间较小，此时收敛速度不会有很大提高。

参数α、β变化对收敛速度和稳态误差的影响如表1所示。本文选择α=3、β=1。

表1 参数变化对收敛速度和稳态误差的影响

2.2.2 引入绝对估计误差的扰动量Q(n)

为提高算法在未知系统突变时的跟踪速度和抗噪性能，基于上述步长因子μ′(n)与误差信号e(n)间的函数关系，本文在权向量w(n)的更新过程中引入绝对估计误差的扰动量Q(n)，此时权向量w(n)的更新公式为

w(n+1)=w(n)+2μ′(n)e(n)a(n)+Q(n)

(9)

Q(n)=kγ(n)(|e(n)|-|e(n-1)|)

(10)

γ(n)=pγ(n-1)=…=pnγ(0)

(11)

式中：k为单位列向量，维数与权向量w(n)相同；γ(n)>0，定义为扰动量的幅度因子，按式(11)的形式衰减，其衰减系数|p|<1。

算法利用幅度因子γ(n)把扰动量Q(n)对权向量w(n)的调节保持在一个最优值。同时，选用绝对估计误差|e(n)|表征估计信号偏离期望信号的程度。

在算法初次迭代时，扰动量Q(n)的幅度因子γ(n)较大，因此扰动量Q(n)对权向量w(n)的更新影响明显。随着迭代次数的增加，γ(n)逐渐减小并逼近于0，e(n)的轻微波动将不会对权向量w(n)的变化造成影响，从而使稳态误差处于较低水平。当系统发生突变时，扰动量Q(n)通过对权向量w(n)进行正反向调节提高收敛速度，即无论干扰信号多大，算法都保持良好的跟踪速度，快速达到较小的稳态误差，拥有较强的抗噪性能。

2.2.3 算法的收敛速度及抗噪性能分析

为检验本文算法同其他算法在收敛速度和抗噪性能方面的优劣，对算法进行仿真实验，并选取传统LMS算法、文献[6]和文献[7]中不同算法作对比实验。

文献[6]提出的改进SVSLMS算法为

(12)

文献[7]提出的基于t分布的改进LMS算法BVTLMS为

(13)

具体实验条件为：

(1)自适应滤波器的阶数M=2；

(2)参考输入信号a(n)是均值为0、方差为1的白噪声；

(3)干扰信号v(n)是均值为0、方差为0.04的白噪声，且与参考输入信号不相关；

(4)每次的迭代次数为600，分别做100次独立的仿真，求其统计平均得出学习曲线；

(5)设定未知系统滤波器的抽头参数为[0.8，0.5]，在第300次迭代时刻未知系统发生突变，抽头参数变化为[0.4，0.2]；

(6)传统LMS算法中取μ=0.001，改进的SVSLMS算法中取α=5、β=1、γ=2，BTVLMS算法中取α=3、β=2、η=0.0001，本文算法中取α=3、β=1、γ(0)=0.4、p=0.4。

由文献[10]可知，算法的收敛速度可由均方误差与迭代次数的关系曲线表示。算法达到稳态时的迭代次数越少，则其收敛速度越快。传统LMS算法、文献[6]算法、文献[7]算法和本文算法迭代0到600次时的学习曲线对比如图6所示。

图6 不同算法的学习曲线

由图6可见，文献[6]算法和文献[7]算法的学习曲线几乎重合。随着迭代次数的增加，传统LMS算法由于其步长固定，在迭代250次左右完成收敛过程，收敛速度最慢。文献[6]和文献[7]算法在第90次和第80次迭代后完成收敛。本文算法收敛速度最快，在迭代50次左右完成算法的收敛过程，且在算法收敛后，具有较小的稳态误差值。

为检验本文算法的抗噪性能，即检验收敛后算法在非平稳环境(未知系统发生突变)下的跟踪能力，设定未知系统初始的抽头参数为[0.8，0.5]，在第300次迭代时系统的抽头参数变化为[0.4，0.2]。

抗噪性能测试实验的前提为算法收敛后，未知系统发生突变。由上述收敛速度测试实验结果可知，四种算法均在300次前收敛，满足该前提条件。由图6可知，在未知系统发生突变后，传统LMS算法在第480次迭代后完成收敛过程，跟踪速度最差，抗噪性能不好；文献[6]和文献[7]算法在第370次和第350次迭代后完成收敛；本文算法在面对未知系统突变时，仅第330次迭代后完成收敛过程，有较好的跟踪能力，即较强的抗噪性能。

通过以上仿真可以看出，本文算法在迭代初期，拥有较快的收敛速度，当算法收敛后，有较小的稳态误差，在外界环境变化时，有较快的跟踪速度和较强的抗噪性能。

3 自适应噪声抵消系统仿真平台设计

本文利用Matlab的GUI工具设计了自适应噪声抵消系统仿真平台，并将传统LMS算法、文献[6]算法、文献[7]算法和本文提出的基于Softsign函数的新变步长LMS算法应用在噪声抵消系统中，进一步研究四种算法的去噪效果。

3.1 系统仿真平台的设计

自适应噪声抵消系统仿真平台设计框架如图7所示。

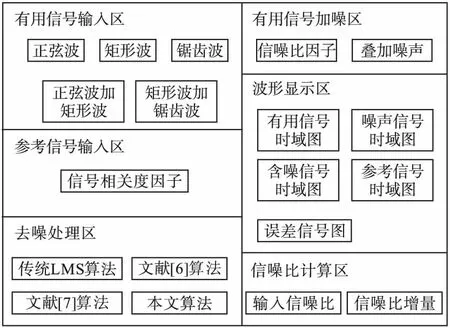
图7 自适应噪声抵消系统设计框图

该平台主要实现对有用信号、噪声信号和参考信号的读写、显示等基本操作以及对含噪信号的去噪处理相关操作，分为有用信号输入区、有用信号加噪区、参考信号输入区、去噪处理区、波形显示区和信噪比计算区6个模块。

(1)有用信号输入区。用户可在正弦波、矩形波、锯齿波、正弦波加矩形波和矩形波加锯齿波中选择需要处理的有用信号，波形显示区会自动生成该信号的时域波形图。

(2)有用信号加噪区。本文选用均值为0、方差为1的白噪声作为噪声信号，并用信噪比因子调节其方差值，点击“叠加噪声”按钮后，会在波形显示区出现噪声信号及含噪信号的波形图，同时在信噪比计算区显示此时输入信噪比的数值。

(3)参考信号输入区。本文选用与噪声信号相关的参考信号输入，并通过相关度因子调节噪声信号与参考信号二者间的线性相关情况。

(4)去噪处理区。在2.2.3中已证明本文提出的基于Softsign函数的变步长LMS算法可以很好地兼顾收敛速度和抗噪性能。在去噪处理部分，用户可以在确定信噪比因子、步长因子等参数后选择传统LMS算法、文献[6]算法、文献[7]算法或本文提出的算法进行相应的去噪处理。

(5)波形显示区。系统运行后，参考信号和去噪处理后的误差信号等会直接显示在波形显示区。

(6)信噪比计算区。为客观评价自适应噪声抵消系统的去噪效果，本文选定信噪比作为评价自适应噪声抵消系统性能的一个重要指标[11]。定义本文中系统的输入信噪比SNRin为主通道中有用信号s(n)的功率与噪声信号n0(n)的功率之比，并将其结果取以10为底的对数，表达式为

(14)

输出信噪比SNRout为有用信号s(n)与经过自适应抵消系统后的剩余信号e(n)-s(n)的总功率之比，并将其结果取以10为底的对数，表达式为

(15)

信噪比增量为

ΔSNR=SNRout-SNRin

(16)

3.2 自适应噪声抵消系统仿真平台运行结果与分析

有用信号为正弦信号，首先输入有用信号，设定信噪比因子的值(在本次实验中设定为1)，显示叠加噪声后的含噪信号，确定信噪比相关度的值(在本次实验中设定为1)，输入参考信号进行去噪处理。此时的有用信号、噪声信号、含噪信号和参考信号的时域波形图如图8所示。应用步长为0.001的传统LMS算法、文献[6]算法、文献[7]算法和本文基于Softsign函数的新变步长LMS算法的误差信号时域波形图如图9所示。

图8 各信号时域波形图

图9 4种算法误差信号时域波形图对比

由仿真平台运行结果可知，输入信噪比为-2.95dB，应用四种算法的自适应抵消系统信噪比增量分别为13.71、17.16、17.48和19.03dB，均有一定的去噪效果，可提高信号传递和接收的信噪比质量。

为检验信噪比因子和信号相关度因子的变化对系统去噪的影响，首先保持信号相关度因子始终为1，将信噪比因子的值从1设置为1.1。此时的输入信噪比随信噪比因子变化为-3.84dB，应用四种算法的自适应抵消系统信噪比增量分别为14.34、17.83、17.99、19.27dB。其次保持信噪比因子为1不变，改变信号相关度因子的值，将其值从1设为1.1。此时的输入信噪比仍为-2.95dB，应用四种算法的自适应抵消系统信噪比增量分别为13.56dB、16.06dB、16.23dB、16.78dB。由此得出，当信噪比因子和信号相关度因子变化时，应用本文算法的自适应抵消系统去噪效果始终优于应用传统LMS算法、文献[6]算法和文献[7]算法的自适应抵消系统去噪效果。

当输入的有用信号变为其他波形时，应用四种算法的自适应抵消系统的信噪比增量对比如表2所示。其中噪声信号取均值为0、方差为1的白噪声，信噪比因子和信号相关度因子的取值均为1，滤波器阶数为2，传统LMS算法的步长为0.001。

表2 不同有用信号下的信噪比增量对比 dB

由表2可知，在五种不同的有用信号下，应用四种算法的自适应抵消系统均有较好的去噪效果。应用本文算法的自适应噪声抵消系统去噪效果均优于传统LMS算法、文献[6]算法和文献[7]算法的自适应抵消系统去噪效果，且噪声信号干扰越强烈，应用本文算法的自适应噪声抵消系统去噪效果越明显，在正弦波及锯齿波有用信号输入时，信噪比增量达到19～20dB。

4 结论

分析了传统LMS算法及多种变步长LMS算法性能，提出了一种新变步长LMS算法。该算法首先基于Softsign函数建立了步长因子与误差信号间的函数关系，分析了参数α、β对步长因子取值的影响，引入了绝对估计的扰动量以应对未知系统的突变情况。仿真结果显示，本文提出的算法较传统LMS算法、文献[6]算法和文献[7]算法具有收敛速度更快和抗噪性能更强的优势。设计了自适应噪声抵消系统仿真平台，实现了噪声叠加、信噪比计算等功能，将新算法应用于该仿真平台中，验证了其具有较好的去噪效果，在噪声控制领域有一定的使用价值。