“情境引入探究教学法”的理论与实践
2022-08-10吴照奇朱传喜
吴照奇,屈 泳,朱传喜
(南昌大学,江西 南昌330031)
文章首先指出目前综合性本科院校“数学文化”课程面临的主要困境,并回顾关于“数学文化”课程改革和数学教学法的若干理论研究和实践探索。其次,阐述“情境引入探究教学法”的理论依据和主要操作流程。最后,通过具体教学案例展示该教学法如何运用。
一、“数学文化”课程的建设和面临的主要困境
“数学文化”课程主要以数学知识为载体来讲授数学的思想、精神、方法和观点。在国内,“数学文化”课程最早由南开大学顾沛教授于2001年开设,此后,国内多所高校相继开设此类课程。南昌大学从2005年开始开设数学文化类课程,包括“数学文化”与“数学学科导论”等,积累了一些经验[1]。除线下课程外,多所高校也陆续开始建设数学文化类在线开放课程,如南开大学顾沛教授的“数学文化十讲”、北京航空航天大学李尚志教授的“数学大观”、上海交通大学王维克教授的“数学之旅”、浙江大学蔡天新教授的“数学传奇”、南昌大学朱传喜教授的国家精品视频公开课“走近科学女王——数学”和国家精品在线开放课“聪慧的源泉——数学导读”等。其中,朱传喜教授作为负责人的“聪慧的源泉——数学导读”自2015年开始在教育部官网爱课程平台上线,目前已开设13期,反响很好。该课程同时作为南昌大学II类通识课供校内学生选修。2008年,由顾沛教授主编的《数学文化》教材出版,该教材注重知识性、趣味性、应用性和思想性的统一,以及科学素质教育与人文素质教育的有机融合,贴近教学实际[2]。2017年,《数学文化》(第2版)出版,这是作者在15年教学实践的基础上逐渐修改完善而成的,本次修订与“数学文化”课程紧密结合,将纸质教材与数字化资源一体化设计以新形态教材形式出版[3]。
杨叔子院士认为“数学文化”课程建设在推进素质教育中具有重要意义和价值[4]。顾沛介绍了南开大学“数学文化”课程的创建及其在全国推广的经验和做法[5]。朱长江、李书刚、胡中波介绍了华中师范大学在“数学文化”课程中引进优质网络教学资源开展混合式教学的经验[6]。吴照奇、朱传喜讨论了复合型人才培养视角下的“数学文化”教学改革与实践及如何在数学专业课程中渗透数学文化[7-8]。朱长江和朱传喜探讨了如何利用数学文化类课程提高学生的数学素养[9-10]。
在社会竞争日益激烈的时代背景下,复合型人才的培养成为迫切需要。在这一视角下,目前综合性本科院校“数学文化”课程教学仍然面临以下突出问题。
第一,作为全校公共选修课(Ⅱ类通识课),选课学生涵盖各个专业,数学基础不同,对数学的感知和理解有显著差异。
第二,部分学生对数学有恐惧和畏难心理,认为数学是枯燥乏味、艰深晦涩、高不可攀的,在课堂互动时参与感不强,热情不高。
第三,长期以来的应试教育导致学生对数学的思想、方法知之甚少,谈不上具有数学素养,不符合复合型人才培养要求。
通过与兄弟院校的交流发现,这些问题在本科院校开设数学文化类通识课的过程中普遍存在,且亟待解决。在这一背景下,文章通过理论创新和实践探索,解决以上问题。
二、“情境引入探究教学法”的相关研究和理论依据
目前,数学教学法已有“情境教学法”的相关研究。例如,张惠英提出“四环节”课堂活动模式:创设问题情境—学生自主探究—辨析与研讨—反思与评价[11]。曾小平、汪秉彝、吕传汉明确了数学“情境—问题”教学实践探索出的探究学习模式有“质疑—挑战”“猜想—论证”“感悟—发现”“探索—讨论”等[12]。此外,也有许多学者对数学探究性学习和探究性教学进行了深入研究[13-15]。
“深度学习”这一概念最早是由美国学者马顿和塞利约于1976年基于记忆和非批判性接受知识的浅层学习而提出的[16]。此后,大量学者对深度学习进行了系统而深入的研究,但学界对于其内涵并未形成统一认识。根据布鲁姆对认知领域学习目标的分类,即知道、领会、应用、分析、综合及评价6个层次,何玲、黎加厚指出深度学习对应布鲁姆认知领域学习目标分类中的应用、分析、综合、评价,并概括出深度学习具有理解与批判、联系与构建、迁移与应用这3个特征[17]。张浩、吴秀娟着重分析了建构主义、情境认知理论、分布式认知理论和元认知理论这四大理论与深度学习的关系[18]。郭华指出深度学习具有以下5个特征:(1)联想与结构:经验与知识的相互转化;(2)活动与体验:学生的学习机制;(3)本质与变式:对学习对象进行深度加工;(4)迁移与应用:在教学活动中模拟社会实践;(5)价值与评价:“人”的成长的过程要素[19]。
美国研究院(AmericanIn stitutes for Research)最新研究成果表明[20],深度学习是学生对核心课程知识的深度理解并将其应用于真实问题和情境中的能力。此处所述能力主要包括3种:一是认知能力,即深度理解内容知识、批判性思维与复杂问题解决能力;二是人际能力,即协作与交流;三是内省能力,即学会学习和学术信念。
基于上述观点,朱先东认为深度学习是基于学生对学习主题的理解,以解决挑战性问题和发展高阶思维为目标的学习,即通过对核心内容的分析和教材的整合,以及学生高阶认知参与,获得知识、过程、方法、价值的深度感悟,完善和发展认知结构,形成学习能力,并能将这种能力迁移到新的情境中,有效解决挑战性问题的学习,其在此基础上,提出了基于深度学习的数学整体性教学设计的理念和具体实施方法[20]。
20世纪90年代以来,国内探讨数学素养内涵的研究呈现多元化趋势,主要包括成分说、后天训练说、实践内化说、生活说等不同形式。黄友初指出,2010年以来,我国学者对数学素养的内涵有了相对统一的认识,包括数学素养称谓的统一化和数学素养的生活说逐渐得到广泛认同[21]。生活说强调的是个体要在生活中有意识地应用数学,认识到数学在现实生活中发挥着巨大作用。
“数学文化”课程的主要目的是提升学生数学素养。由上可见,数学素养与深度学习有内在相通的思想和理念。文章提出的“情境引入探究教学法”主要针对“数学文化”课程,共包含5个重要环节,强调情境引入和自主探究,以深度学习和布鲁姆目标教学法为理论依据和支撑。该教学法与已有教学法有相似之处,但其灵魂与精髓在于后两个环节,这是能否最终实现学生数学素养提升的关键所在。
三、“情境引入探究教学法”的操作流程
针对“数学文化”课程的特点,创立了“数学文化”课程“情境引入探究教学法”。这一方法的具体内涵为:通过创设具体情境的数学问题,进行数学思维方法的渗透,引导学生自主探究数学在实际问题中的应用,提高学生理论联系实际和协作交流的能力,不断提升学生数学素养。本方法主要操作流程共分为5步,如图1所示。
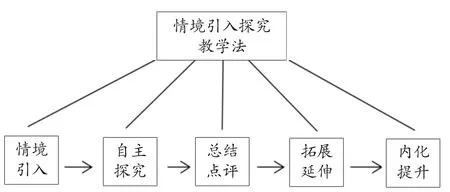
图1“情境引入探究教学法”操作流程
1.情境引入:首先,精心挑选或创设具体情境,将数学问题转变为有具体情境的实际问题,将问题展示给学生,让学生了解问题大意。
2.自主探究:首先将学生进行分组,组内学生先独立思考,有想法后进行组间讨论,必要时可给学生一些提示。这一步的关键是教师只能引导,不能急于给出答案,要让学生自主探究。学生会从各个角度进行尝试,有些尝试可能是失败的,但这并无妨碍,因为重点是要让学生享受主动探索的过程。
3.总结点评:让学生思考、讨论一段时间后,各组选派一个代表发言。一般先挑选1~2个小组代表对问题的解决进行阐述,然后让组内学生进行补充,再让其他小组学生进行生生互评,互相启发,最后再由教师进行点评。这一步一方面是训练学生在探索问题时反复求证和完善的能力,另一方面是训练学生用准确、简明、清晰的数学语言表达自己思想的能力。教师在总结点评时要让学生比较教师的表述与学生的表述有何区别,体会哪种表述更好。小组讨论环节的设置,目的是增强学生团队合作意识。
4.拓展延伸:很多问题并不是孤立的,因此在问题得到解决后,要趁热打铁。首先让学生思考是否还有其他方法和途径来解决这一问题;其次,这一问题是否可以进一步拓展和延伸,该如何解决。这样,学生就不会出现“一叶障目,不见森林”的状况,而是达到“通过一棵树木收获一片森林”的效果。
5.内化提升:本环节首先要让学生思考,上述具体情境的问题是否可以抽象为一个纯数学问题,作为纯数学问题,答案是什么。同时,让学生再回味在解决上述问题及其推广的过程中,使用了什么数学方法,体现了什么样的数学思想,有何特色和妙处,是否可以解决类似或相关问题。只有引导学生进行这些思考,才能让数学的思想和方法深入骨髓,溶入血液,内化提升为学生自己的数学素养。
“情境引入探究教学法”主要用于课堂教学,但相关的互动讨论和拓展延伸亦可放在线上,如网络教育平台或者在线课程平台上,以弥补课堂教学学时的不足。通过线上线下相结合的教学模式,可最大程度地实现教学目标。
四、教学案例:量杯量水问题
(一)情境引入
向学生介绍如下外企招聘题。
问题1:给定足量的水、3升量杯和5升量杯,如何量出4升的水?
(二)自主探究
将学生进行分组,让每组学生先自主探究,再交流想法。本题的提示为:注意水是足量的,因此,量杯盛满后可以倒掉然后再注入水,并可反复进行。
(三)总结点评
教师示意学生主动举手发言。如第一组学生代表发言如下。
“先将3升量杯装满,倒入5升量杯,再将3升量杯装满,倒入5升量杯,将5升量杯的水倒掉。将3升量杯中剩余的水倒入5升量杯,再将3升量杯装满,倒入5升量杯中。”
该学生发言完毕后,示意同组学生是否有补充。有学生表示最后一句应该说明确一些:“这时,5升量杯中的水为4升。”教师再选第二组学生代表发言,进行重新表述,具体如下。
“先将3升量杯装满,倒入5升量杯,再将3升量杯装满,倒入5升量杯,这时3升量杯中剩余1升水。再将5升量杯中的水倒掉。将3升量杯中剩余的1升水倒入5升量杯,然后,再将3升量杯装满,倒入5升量杯中。这时,5升量杯中的水为4升。”
教师可让其他各组学生对以上两位学生的发言进行点评,其他学生表示无进一步补充。此时,教师可进行总结和点评。首先,应肯定学生给出的答案是正确的,表述也是基本准确的,但需稍加完善。教师对这一方案进行重新表述。
解决方案1:先将3升量杯盛满,倒入5升量杯,再将3升量杯盛满,倒入5升量杯,直到5升量杯盛满为止,这时3升量杯中剩余1升水。再将5升量杯中的水倒掉。将3升量杯中剩余的1升水倒入5升量杯,然后,再将3升量杯盛满,倒入5升量杯中。这时,5升量杯中的水恰好为4升。
让学生比较表述的不同,关键是要加上“直到5升量杯盛满为止”这句话才比较准确。
(四)拓展延伸
1.让学生思考除上述方案外,是否还有其他方案解决这一问题?
给学生一定时间进行思考后,重新挑选未发言的学生发言,并进行点评。学生在经过前一轮的自主探究后,基本能比较准确地给出如下方案。
解决方案2:先将5升量杯盛满,倒入3升量杯。再将3升量杯中的水倒掉,将5升量杯中剩余的2升水倒入3升量杯,则3升量杯差1升盛满。再将5升量杯盛满,倒入3升量杯,直到3升量杯盛满为止。这时,5升量杯中的水恰好为4升。
2.这一问题是否可以进一步拓展和延伸,该如何解决?
仔细分析上一环节中问题1的解决方案1,不难发现,问题1实际上可以进一步推广,变成如下更一般的问题。
问题2:如何用一个2n+1(其中n为自然数)升量杯和2n+3(其中n为自然数)升量杯,以及足量的水,量出4n(其中n为自然数)升的水?
这一问题可沿用问题1的解决方案1,只需将解决方案1中的数字3、5、1和4分别替换成2n+1(其中n为自然数)、2n+3(其中n为自然数)、2n-1(其中n为自然数)和4n(其中n为自然数)即可。
再分析问题1的解决方案2,可知问题1又可推广为如下的另一个更一般的问题。
问题3:如何用一个2n+1(其中n为自然数)升量杯和2n+3(其中n为自然数)升量杯,以及足量的水,量出4升的水?
同理,问题3的解决方案只需将问题1的解决方案2中的数字5、3和1分别替换成2n+3(其中n为自然数)、2n+1(其中n为自然数)和2n-1(其中n为自然数)即可。
(五)内化提升
问题1如何抽象为一个纯数学问题?引导学生思考后,教师给出回答:问题1的本质是如下数学问题。
问题1':给定数字3和5,如何用这两个数字(可反复使用多次),以及加、减运算,得到数字4?
抽象为上述数学问题后,解题归结为两种思路,即3+1=4和5-1=4。这样,两套方案可以分别用如下两个等式来表示:
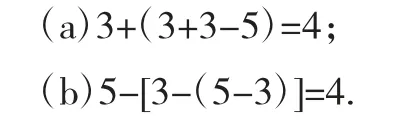
问题2可抽象为如下数学问题。
问题2':给定数字2n+1(其中n为自然数)和2n+3(其中n为自然数),如何用这两个数字(可反复使用多次),以及加、减运算,得到数字4n(其中n为自然数)?
问题2'的解决方案可用如下等式来表示:

同理,问题3也可抽象为如下数学问题。
问题3':给定数字2n+1(其中n为自然数)和2n+3(其中n为自然数),如何用这两个数字(可反复使用多次),以及加、减运算,得到数字4?
而问题3'的解决方案可用如下等式来表示:
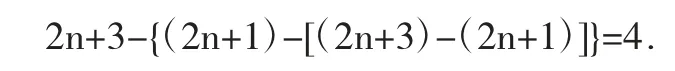
从具体情境的实际问题到数学问题,体现了抽象化的数学思想。上述几个等式对应相应的解决方案,但等式显然更简洁明了,这又体现了数学的简洁美。在解决问题的过程中,也体现了以下两点素养:(1)对各种问题运用“数学方式”的理性思维,从多角度探寻解决问题的方法;(2)善于对现实世界中的现象和过程进行合理的简化和量化,建立数学模型。这是教育部高等学校数学与统计学教学指导委员会给出的数学素养基本内涵中的两条。
“情境引入探究教学法”主要以创设具体情境的实际问题为载体来展示数学文化,这些问题的本质是数学问题。该教学法的核心是“自主探究”,目标是提升学生数学素养,即强调通过学生自主探索而有所收获。在操作流程的5个环节中,前3个环节是解决原始情境问题的基本环节,第四个环节“拓展延伸”是对前3个环节的推进,而最后一个环节“内化提升”又是前4个环节的进一步深化。学生是否能够通过情境问题实现数学素养的提升,关键在于后两个环节是否能够有效设计和实施。
纵观“情境引入探究教学法”的基本流程可知,该教学法的运用,能有效提高学生数学素养,契合目前“复合型人才培养”的新理念,故具有鲜明的时代性;5个环节环环相扣,层层递进,有机融合,缺一不可,故又具有高度的融合性;该教学法的亮点在后两个环节,具有典型的创新性;5个环节均内涵清晰,步骤明确,有较强的可操作性。因此,只要合理地、恰到好处地运用这一方法,就能有效开展本科院校“数学文化”课程教学,有力促进本科院校“数学文化”课程的改革,为培养更多复合型创新人才贡献力量。
