基于改进卷积神经网络的图像畸变快速校正算法

李云波, 李晓峰*, 李 东, 卫 晋

(1. 黑龙江外国语学院 信息工程系, 黑龙江 哈尔滨 150025;2. 哈尔滨工业大学 计算机科学与技术学院, 黑龙江 哈尔滨 150001;3. 北京理工大学 计算机科学与技术学院, 北京 100081)

在信息化时代,图像的重要性逐步凸显,然而市场中的摄像机质量参差不齐,采集到的图像质量也不相同[1-2]。摄像机成像会受到很多因素的影响,包括摄影过程中实体景物与摄像机的相对运动、大气湍流效应、周边环境的色彩噪声等[3-4],由这些因素所导致的图像失真问题被称之为图像畸变[5]。由于计算机科学发展迅速,很多图像畸变问题已经可以使用软件程序调整[6-7]。

当前对于图像畸变校正方法的研究已取得了一些有效的成果。文献[8]首先分析了投影图像之间的几何位置关系,采用网格划分法对畸变图像进行校正,然后采用边缘衰减算法来对图像进行边缘融合处理,并且通过过滤消除多源投影中球幕图像上的亮带,使投影图像的整体亮度保持均匀,但图像畸变校正耗时较长。文献[9]使用FPGA技术设计了一个图像畸变校正算法,并利用线性插值技术获取了映射的逆向容量坐标,在映射表中通过调整压缩参数保证图像数据的完整性与安全性,但计算准确度不够高。文献[10]通过对鱼眼图像有效区域进行划分,并对不同区域内的畸变点在横、纵2个方向上分别建立校正模型,确定畸变图像与理想图像之间的坐标映射关系,求取校正坐标的位置。最后对图像进行非线性拉伸,改善图像中心与边缘放大率不同而产生的“膨胀感”,获得符合人眼视觉习惯的图像,但对于畸变图像像素点定位效果还有待优化。文献[11]通过对透射电子显微镜图像畸变进行分析,以及其对应关系进行多项式变换,求出多项式拟合后最小误差,获取电子显微镜畸变测度,采用电子显微镜图像自适应的惯性权重,以适应度值来对惯性权重大小进行调节,以最优粒子作为全局最优解,完成图像畸变快速校正,整体效果较好,但存在耗时较长的问题。文献[12]采用光电测量技术对复眼系统进行畸变测量与校正,生成多模动态电子畸变测量靶标,构建畸变测量校正模型,建立多项式拟合算法,采用最小二乘法获得畸变系数,通过双线性插值法模型对图像进行重建,但网络损失值较大。

以上方法在定位像素点时的准确度较差,导致校正效果不理想,因此本文提出了基于改进卷积神经网络的图像畸变快速校正方法。本研究的主要贡献如下:①根据图像中心点计算畸变图像像素点坐标值,解决传统方法像素点定位不准确的问题。②利用改进卷积神经网络校正畸变图像像素点,得到像素点偏移坐标以及偏移距离,以此获取更为准确的像素点定位结果。③利用不同函数指令实现图像畸变快速校正,降低校正耗时,提升校正速度。

1 基于改进卷积神经网络设计图像畸变快速校正方法

1.1 计算畸变图像像素点坐标值

在摄像机的投影系统中,为了收集更多信息,在相机的投影模型中需要遵循

Rx=hjjtanθx。

(1)

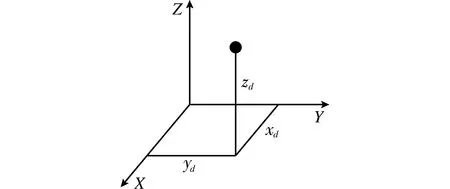
图1 笛卡尔坐标系Fig.1 Cartesian coordinate system

式中:Rx表示摄影图像中的任意一个像素点到图像最中心的直线距离;hjj表示摄影机的焦距;θx表示光线通过摄影机后与光轴形成的夹角。通过这样的投影模型,可以提升摄像机拍摄的面积[13]。从另一个角度出发,假设被摄像机拍摄的畸变图像分辨率为Xk×Yk,其中,Xk表示图像中第k个像素点在高度中的坐标,Yk表示图像中第k个像素点在宽度中的坐标。由此可以将像素点的坐标系与笛卡尔坐标系相互转化,笛卡尔坐标系如图1所示。

具体的转化公式为:

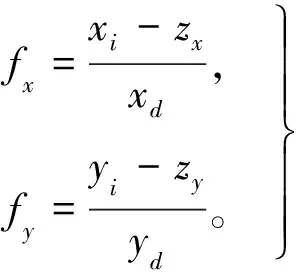
(2)

式中:fx和fy分别表示图像像素坐标值在x轴方向与y轴方向的像素格数量;xi与yi分别表示图像像素坐标在x轴与y轴方向的坐标;zx和zy表示图像中心点的坐标;xd和yd表示该像素点的笛卡尔坐标位置[14]。该像素点至图像中心点的距离为

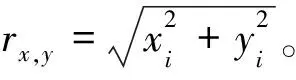
(3)

式中:rx,y表示畸变图像的任意一点到图像中心点的距离,此时得到投影模型为

(4)

式中:Rn表示畸变图像的像素点n与正常图像像素点之间的直线距离;fn表示畸变图像中像素点的数量;θn表示光线在通过镜头后与像素点形成的入射夹角。畸变参数为

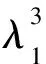
(5)

式中:λn表示畸变图像像素点的位置参数;δxy(λn)表示图像的畸变参数;λ0～λ3分别表示入射光线在几次反射之后的光线角度;R1～R3则表示入射光线行走的半径[15]。以畸变参数计算结果为基础,可以依据正常的图像像素点提取畸变图像的像素点坐标值。

1.2 基于改进卷积神经网络的畸变图像像素点校正

卷积神经网络是一种新型深度卷积结构,在图像分析中具有非常好的应用性,对于不同大小和类型的图像均具有很好的适用性。但卷积神经网络在训练过程中容易出现过拟合问题,因此对其进行改进,采用反向传播算法实时调整参数,完成权值更新,进而实现图像处理。改进卷积神经网络结构模型如图2所示。

图2 改进卷积神经网络结构模型Fig.2 Structure model of improved convolutional neural network

以图2改进卷积神经网络结构模型为基础,对畸变图像像素点进行误差校正。误差校正是一种将输出误差强行稳定在神经元中的一种修正算法。设输出样本为(Fd,Uk),其中,Fd可以作为网络输入的连接节点,Uk则表示网络输出的连接节点。网络权值的修正量为

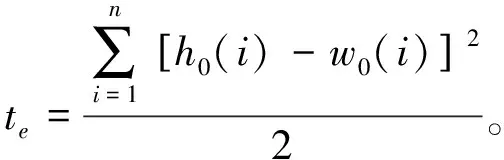
(6)

式中:te表示网络权值的修正结果;h0(i)表示网络神经元的输出误差;w0(i)表示网络神经元的输入误差。此时神经元的连接权值与修正结果之间存在关系

Δμdk=te(γhνkim)。

(7)

式中:Δμdk表示在结果修正以后连接权值的调整量;μdk表示连接权值;γh表示神经元连接的效率;νk表示神经元的输出效率;im表示误差函数在经过神经元过程中的偏导数因子[16]。

在改进卷积神经网络的隐含层和输入层中,可以将像素坐标标记为(xi,yi),此时的输入与输出向量可以作为影响因子的维度,因此隐含层的数量必须超出一定的阈值[17-18]。在畸变图像像素点的投影中,若投影点映射在正常图像中,则投影点可以以一种倾斜的方式平移到另一个方向,可以从其中选取两条平行线,就会将其中一个像素点变为精准的垂直函数,此时存在关系

(8)

式中:D1(xi,pk)表示2条像素点构成的线段在相互垂直的前提下组成的变量交叉函数;xi和pk分别表示一条垂直线;H(xi,pk)表示像素点的平移间距。若某一个图像畸变像素点出现了一个投影峰值,则像素单元的倾斜角度可以表示为

(9)

式中:φx表示投影面上像素点的与畸变图像之间的倾斜角度;Ds表示畸变图像像素点与正常图像像素点在统一投影面上的间距;Ud表示图像噪声峰值面积。此时若通过霍夫变换将像素点全部映射到参数空间,就可以通过累加和的方式获得所有像素点的倾斜方向,并以对偶的方式定义图像空间中的曲率[19]。通过曲率可以得到图像校正过程中像素点偏移距离为

(10)

式中:ρx,y表示经过校正后的像素点位置坐标;x0和y0表示校正后的坐标;x1和y1表示校正前的坐标;vi表示像素点的拟合偏移速度。至此应用式(10)即可校正畸变图像中的像素点。

1.3 设计图像快速校正算法

在图像的处理过程中,由于像素点数量庞大,导致数据集的训练以及测试时间较长,为加快图像校正的速度,可以设计一个改进卷积神经网络算法,用于图像畸变的快速校正。在快速校正算法中,只需要经过3个层面,从输入层的像素点输入开始,经过隐含层的修正与求和,最后从输出层输出[20]。在连接权中需有一个激活函数,处理偏置的求和信息。该激活函数为

(11)

式中:hu表示激活函数;ξxy表示像素点在x轴与y轴中的连接函数,在隐含层中起到抑制图像畸变的作用;et表示喜好的线性组合偏置模型参数[21]。经过以上3个层面的数据处理,可以将改进卷积神经网络中的函数分为两类,分别是区域线性函数和非线性函数。其中线性函数的关系式为:

(12)

而非线性函数的关系式则可以表示为:

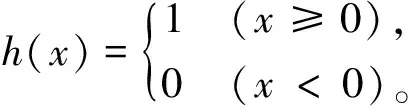
(13)

此时通过这些函数的指令,就可以快速校正畸变图像,并将未经过校正的图像输入输入层,经由隐含层传递到输出层中,此时就能够实现图像畸变快速校正。

2 实验、分析与结果

为了检测文中设计的改进卷积神经网络算法得到的校正结果是否优于文献[8-12]方法,设计如下实验。

2.1 实验环境和数据集

本文所有实验均在Windows 10系统, NVIDIA/英伟达TITAN RTX 24GB,GPU, TensorFlow深度学习框架环境下运行。 采用摄像机拍摄以及MNIST和ImageNet公开数据集中的5 000幅图像进行实验测试, 选取其中图像畸变现象较为明显的2 000幅图像作为实验数据, 其中1 400幅图像用于算法的训练, 400幅图像用于算法检验, 最后200幅图像用于算法测试。 为了使畸变图像具备普适性, 需要在畸变图像的像素点中设置畸变参数{kx,λ1,λ2}, 其中kx表示像素点的总数量,λ1和λ2表示像素点在图像中的位置。将以上畸变参数保存在参数数据集中, 将其与无畸变的参数相比, 可以得到校正参数{u0,xn,yn}, 将所有像素点的校正参数全部保存在同一个数据集中, 就可以得到该图像的参数数据集。

2.2 实验标准

考虑图像像素点数量的庞大以及参数的复杂性,本实验需要消耗大量的时间用于算法训练以及参数校正。在训练实验所有算法过程中,需要一个参与训练的网络参数对样本数据集进行校正。在此过程中,输入的数据是数据集中的畸变图像,输出的则是校正参数。通过损失函数计算网络参数校正值与畸变图像真实值之差

(14)

式中:pi表示第i个样本参数的真实值;wi表示网络参数中第i个样本的校正值;mx表示某图像中的像素点个数;Fmse则表示真实值与校正值之间的差值。 在定义网络参数时, 可以得到损失函数的定义式为

UK=β1U1+β2U2。

(15)

式中:UK表示损失函数,且UK值越小,表明该参数下图像畸变校正的效果越好;β1和β2均为平衡损失值的权重,该权重通过数量级来计算;U1与U2则可以表示校正前的损失值与校正后的损失值。

计算以上损失函数在图像畸变校正过程中的准确性,可以通过观测值拟合度来体现,具体计算公式为

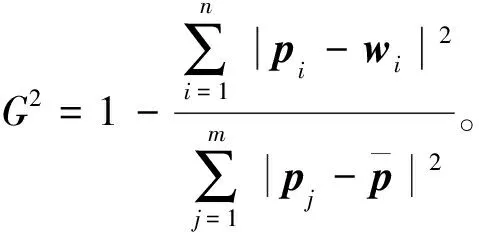
(16)

畸变图像像素点定位准确度是指不同方法定位定位结果与真实像素点位置之间的比率,具体的计算公式为

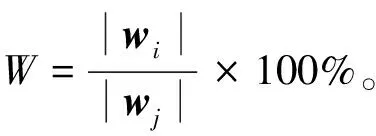
(17)

式中,wj表示真实像素点位置。

图像畸变校正耗时是指完成图像畸变校正所用时间,该指标的公式为

T=T1+T2+…+TN。

(18)

式中,T1,T2,…,TN分别表示不同的图像畸变校正步骤所用时间。

2.3 实验结果

在全网络中,输入的参数个数为256×12×12,且输出的参数总量为256,此时的参数是训练参数正常运行的最大值。为了避免过拟合现象,可以通过随机忽略的方法减少节点间的相互作用,同时在连接层中进行参数训练,通过以上方法可以得到在不断的迭代过程中,6种算法的网络损失函数具体如图3所示。

图3 网络损失函数对比Fig.3 Comparison of network loss function

分析图3可知,在网络损失函数的数据结果中,改进卷积神经网络算法最终的网络损失值约为0.009 2,其他5种对比算法的网络损失值分别为0.031 5、0.020 6、0.040 6、0.011 4、0.020 9。网络损失值的结果越低,表明该参数下的图像畸变校正结果越好,因此在以上6种方法中,本文所设计的改进卷积神经网络算法参数最优。观测拟合度比较结果如图4所示。

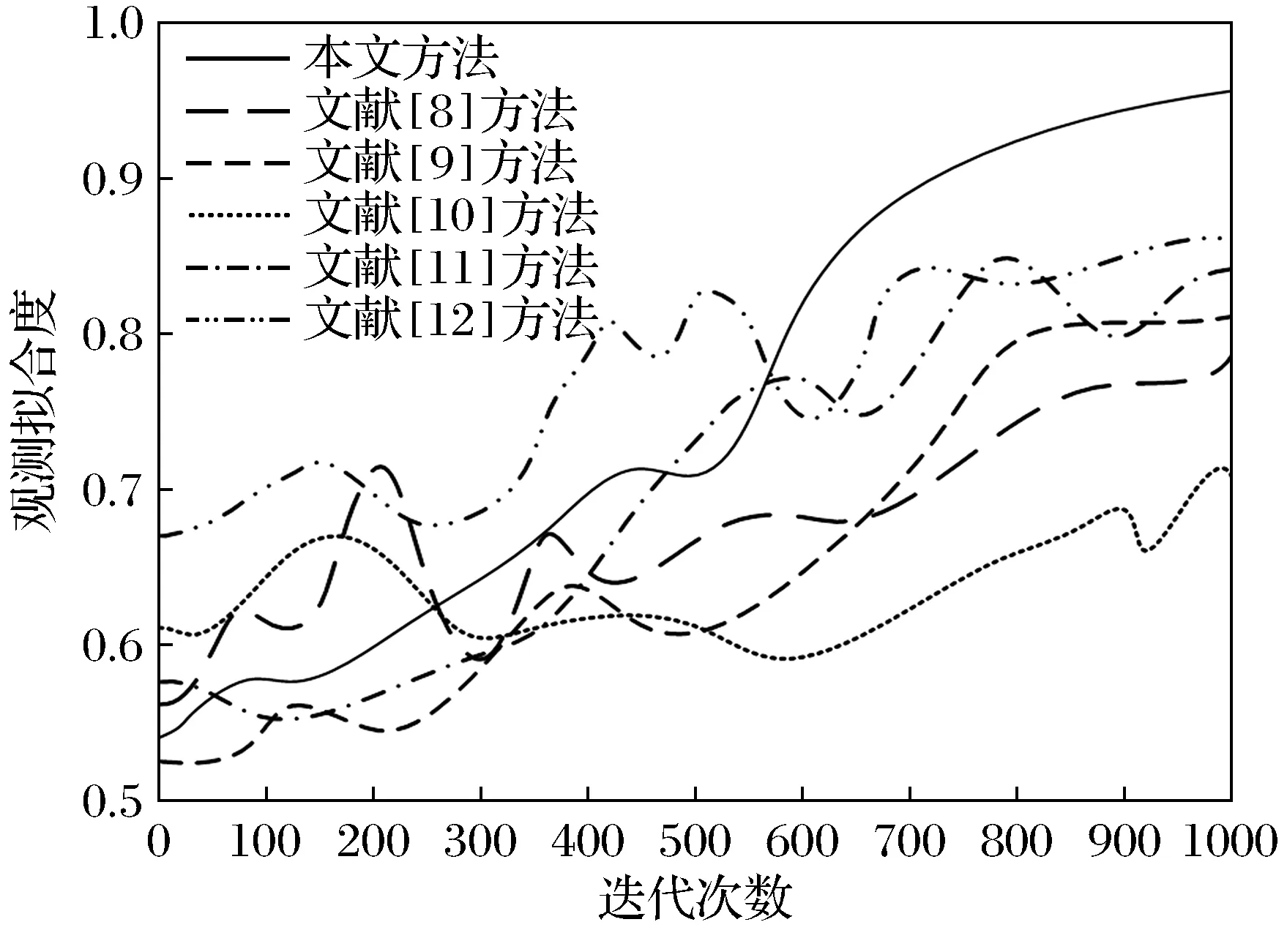
图4 观测拟合度对比Fig.4 Comparison of observational fit

分析图4可知,经过1 000次迭代后,本文方法得到的观测拟合度结果为0.96,其他5种对比方法的观测拟合度分别为0.80、0.83、0.72、0.85、0.86。观测拟合度越接近1,表明该校正参数越准确,因此在6种方法中,本文方法的校正参数准确度最高。因此说明本文设计的基于改进卷积神经网络算法的图像畸变快速校正方法得到的校正参数更佳,校正效果更好。

在上述基础上,选取2幅原始图像进行畸变校正,不同方法的畸变图像校正效果比较如图5～图8所示。

图5 原始图像1Fig.5 Original image 1

(a)文献[8]方法(b)文献[9]方法(c) 文献[10]方法(d)文献[11]方法(e) 文献[12]方法(f) 本文方法

图7 原始图像2Fig.7 Original image 2

(a) 文献[8]方法(b) 文献[9]方法(c) 文献[10]方法(d) 文献[11]方法(e) 文献[12]方法(f) 本文方法

由图5～图8可知,原始图像存在畸变,而本文方法可以有效对畸变处进行校正。

在上述基础上,比较6种方法的畸变图像像素点定位准确度,结果如表1所示。

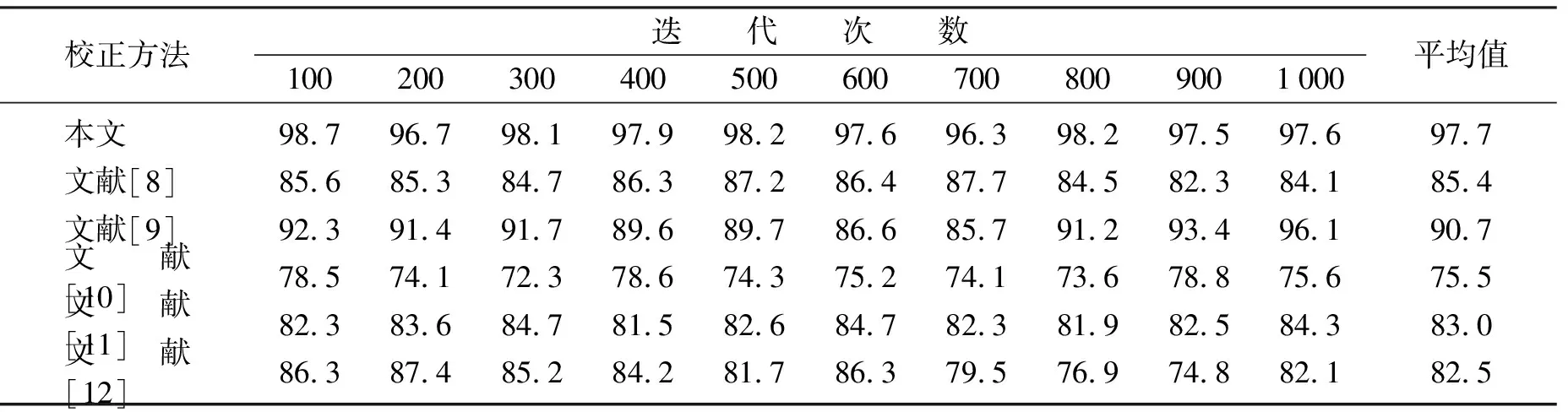
表1 畸变图像像素点定位准确度对比Table 1 Comparison of pixel positioning accuracy of distorted image 单位: %

由表1可知,与文献[8-12]相比,本文所设计方法的畸变图像像素点定位准确度平均值为97.7%,是6种方法中最高的,定位精度高,可以为后续的图像畸变快速校正奠定坚实的基础。

为了进一步验证不同方法的实际应用效果,对图像畸变校正耗时进行了比较,比较结果如表2所示。

表2 图像畸变校正耗时对比Table 2 Comparison of time consumption of image distortion correction 单位: s

由表2可知,与文献[8-12]方法相比,本文所设计方法的图像畸变校正耗时平均值为0.61 s,是6种方法中最低的,说明该方法可以达到图像畸变快速校正的研究目标。

3 结 语

本文以解决传统图像畸变快速校正方法存在的网络损失函数较高、观测拟合度较低、畸变图像像素点定位准确度较低以及图像畸变校正耗时较长的问题,提出了一种基于改进卷积神经网络的图像畸变快速校正方法。通过计算图像像素点的坐标值函数,得到了畸变矫正的模型,以此设计了一种图像畸变快速校正方法,使校正效果更好。实验结果表明,本文方法的网络损失值较低、观测拟合度较高、畸变图像像素点定位准确度较高以及图像畸变校正耗时较短。但本文设计仍有需要改进的地方,如在定义损失函数时,没有考虑到区域像素损失问题,导致最终的结果并不是全局最优解,且在引入图像信息时,没有进一步以非线性的方式优化畸变校正结果,因此在未来的研究中可据此对该方法进行改进与优化。