基于改进灰狼算法使用周期操作制取生物柴油过程的参数优化
2022-08-10史洪岩
史洪岩, 隋 杰
(沈阳化工大学 信息工程学院, 辽宁 沈阳 110142)
生物柴油与石化柴油特性类似,但更加环保,且原料来源广泛,有着良好的社会效益和经济效益,因此受到各国的广泛关注[1]。为了提高生物柴油的转化率,Tabatabaei等[2]从酯交换反应器的角度进行了研究,Norjannah等[3]从酶促生产以及改善酶促反应的方法进行了研究。Prabowoputra等[4]从温度和压力对生物柴油生产过程的影响,以及两者之间相互作用对生物柴油产率影响进行了研究。对于非线性系统,周期操作有可能产生比稳态操作更好的反应性能[5],在一定条件下可以改善系统的时均性,对转化率和产量等有不同程度的提高[6-7]。文献[8]对连续搅拌反应器(CSTR)进行了周期操作,提高了产物的转化率。目前的研究主要集中在周期操作反应转化率的分析和评估上,对于周期操作下系统参数的优化问题研究较少,并且周期操作制取生物柴油的参数研究同样也极为缺乏。生物柴油模型是一个非线性、多模态、高度约束和混合整数的化学反应系统,对其进行周期操作时其参数选择直接影响产物产率,文献[9]表明利用启发式搜索方法分析是解决这类问题最有效、最快、最可靠的方法。自然启发算法[10]具有良好的并行性和自主探索性,极大减少了解决复杂问题带来的时间成本与计算成本,给解决复杂问题提供了一种全新的思路和手段[11]。
本文采用改进的灰狼算法(improved grey wolf optimizer,IGWO)[12]优化单步与同步周期操作生物柴油生产的参数,能够克服普通的灰狼优化算法(grey wolf optimizer,GWO)由于关键狼数量少、缺乏狼群多样性而导致的陷入局部最优[13]的问题,在求解高维、多峰复杂函数问题时,需调整的参数少、收敛速度快和求解精度高,适合全局最优。实验结果证实其求解精度和稳定性均优于GWO算法、蜻蜓算法(DA)、粒子群算法(PSO)和遗传算法(GA),尤其在复杂的优化问题上其优化效果更加稳定,优势更加突出。
1 使用周期操作制取生物柴油
1.1 周期操作
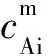

图1 周期操作Fig.1 Periodic operation
1.2 生物柴油制取过程的数学模型
生物柴油过程主要发生的是酯交换反应,反应过程中,1 mol甘油三酯(TG)和3 mol甲醇(A)生成3 mol脂肪酸甲酯(E)和1 mol甘油(GL),过程的简化表述为

(1)
其化学反应原理如图2所示。
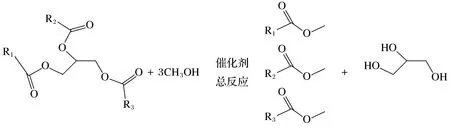
图2 酯交换反应过程Fig.2 Transesterification process
具体的反应过程包括
(2)
式中:甘油二酸酯(DG)和甘油单酸酯(MG)为反应的中间产物;R1,R2和R3是长链烃也称为脂肪酸链;kj,j=1,…,6,表示反应的速度常数。
生物柴油反应过程包括物料平衡方程和能量平衡方程,当涉及n种化学物质的m(n>m)个反应发生时的CSTR动力学,可用式(3)描述,具体的参数含义见文献[14]。
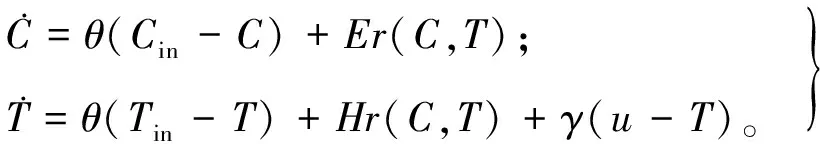
(3)
因此基于CSTR的物料和能量平衡方程为:
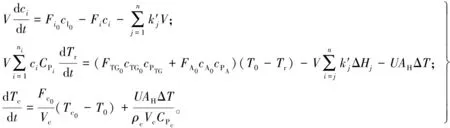
(4)
式中: ΔHj表示各组分的焓变;U表示热传递系数;ρc表示冷却水密度;AH表示热转换面积;ci表示反应过程中各组分的浓度;cI0表示原料初始流量;cA0为初始进料浓度;CPi表示各组分的热容;CPc为冷却流热容;cTG0为初始进料浓度;V为反应器的体积;cPTG为初始甘油三酸酯的浓度;cPA为初始甲醇浓度;Vc为冷却套管容积;Fc0表示冷却水流流量;Fi0表示原料流流量;Fi为反应流的体积流量;FTG0为甘油三酸酯的流量;FA0为甲醇的流量;Tc0为冷却流的初始温度;Tc表示冷却水实时变化温度;Tr为反应器初始温度;T0为反应物的初始温度;ΔT为反应器温度和冷却流温度的温度差值。CSTR模型参数可见文献[15]。
结合式(4),得到生物柴油酯交换反应过程的二阶动力学方程形式[16]如下:
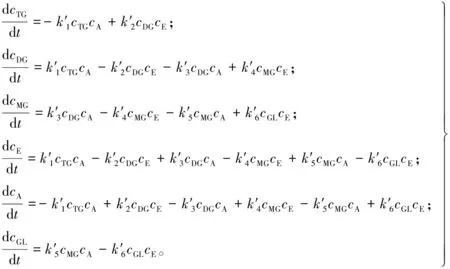
(5)
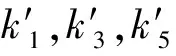
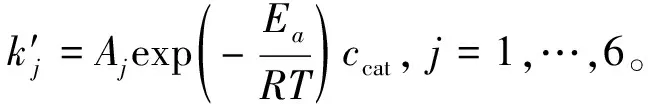
(6)
式中:ccat表示催化剂浓度;Aj和Ea分别是各组分的指前因子和活化能;R为气体常数;T为反应温度。
2 灰狼算法原理
2.1 普通灰狼算法
GWO算法由Mirjalili等[17]在2014年首次提出,是一种元启发式人工智能算法,具有差分进化和引力搜索能力。标准的GWO算法模仿灰狼捕猎的机制,主要模拟了搜索猎物、包围猎物和攻击猎物,具有结构简单、参数少、容易运算的特点。
算法中的狼群模拟了自然中狼群的等级制度,从不同的影响力和领导能力的角度分为4个等级,分别为α、β、δ、ω狼,其中α作为最佳适应度值的候选狼,第2和第3适应度值的候选狼为β和δ,算法中除了上述3种狼,其余的狼总称为ω。狼群在α、β、δ狼的带领下对猎物进行包围寻找,不断迭代更新α、β、δ狼的位置[18]。当狼群发现猎物时,头狼α发出猎杀指令,带领狼群对猎物发起攻击,因为α、β、δ狼位置最靠近猎物,所以根据这3只狼的位置可以判断猎物的位置,也就是最佳狼的位置Xi -GWO。
2.2 改进的灰狼优化算法
经典的GWO算法会使狼群的多样性损失导致过早地收敛从而无法准确的得到全局最优解。IGWO算法增加了基于维度学习的狩猎(DLH)搜索策略,DLH的作用是使群体中每只狼可以向周边狼学习并且进行信息的交换,保证了从种群中公平地选择最佳候选狼,从而增强了局部搜索和全局搜索之间的平衡,保证了个体的多样性,从而更好地搜索整个空间,很好地解决了优化复杂问题性能差等缺点。在IGWO算法中,重新定义了3个不同的步骤,包括:狼群的初始化、狼群的运动、狼的选择和更新。
1) 初始化阶段。N只狼在给定空间中[li,uj]内随机分布并搜索。由式(7)描述。
Xij=lj+randj[0,1](uj-lj),i∈[1,N],j∈[1,D]。
(7)
2) 运动阶段。 IGWO中的狩猎策略为Xi -GWO(t+1)和Xi -DLH(t+1)相结合的方式, 即基于群体狩猎方式和基于维度学习狩猎(DLH)的策略相结合。 使用式(8)计算当前位置Xi(t)与更新后Xi -GWO(t+1)的欧氏距离。 并且使用式(9)构造每只狼的邻域Ni(t)。
式中:Xj(t)的位置与当前迭代的位置Xi(t)相邻;Di为欧氏距离;p为灰狼的种群。由式(10)计算候选狼的位置,并确立建议的更新位置。
Xi -GWO(t+1)=Xi,d(t)+rand(Xn,d(t+1)-Xr,d(t))。
(10)
3) 选择和更新阶段。比较候选狼Xi -GWO(t+1)和Xi -DLH(t+1)的适应度值,最终选出最佳候选狼,可由式(11)描述。
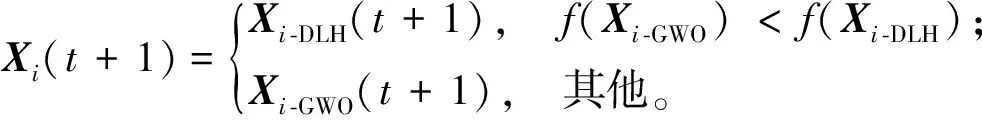
(11)
2.3 优化流程
1) 设置狼群规模、迭代次数,限制条件的上下界,对狼群进行在限制范围内随机分布并初始化。
2) 根据适应度函数计算每一只灰狼的适应度值,并按照适应度选出最好的前3只狼,将目标函数值最优、次优和次次优的个体位置记为Xα、Xβ、Xδ。
3) 根据灰狼的狩猎过程以及式(8)~式(10)计算其他搜索个体与α、β和δ狼的适应度值并且计算其邻域值的灰狼,依次计算其适应度值。
4) 根据步骤3)的适应度值再由式(11)进行比较,选出2者之中较优个体组成下一代种群,由适应度函数确定其中的α、β和δ狼。
5) 检查算法是否满足最大迭代次数或所有个体均已收敛,若条件满足则终止迭代,否则返回步骤3)。
3 周期操作生物柴油过程的参数优化
3.1 周期操作
周期操作是指在一个或几个输入变量稳态值基础上,通过施加周期性变化来实现的。
单输入变量的周期操作一般以正弦波形式给出,
x(t)=x0(t)+Asin(ωt)。
(12)
式中:x0(t)为输入变量稳态值;A为输入周期操作的谐波幅值;ω为周期操作的输入谐波频率。
如果同时对2个输入变量x,y围绕先前建立的稳态xs,ys进行周期性操作时,其表达式形式如下:
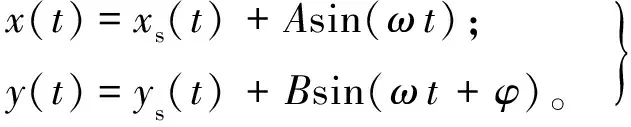
(13)
式中:φ表示2个同步输入变量之间的相位差;B为第2个输入周期操作的谐波幅值。
针对生物柴油生产过程,本文选择反应物流速和冷却液温度进行单步与同步周期操作。
单步输入谐波形式为:
同步输入谐波形式为:
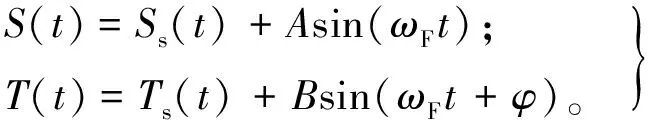
(16)
式中:S(t)为反应物流速;T(t)为冷却液温度;Ss与Ts为各自对应输入变量稳态值,分别为0.119 m3·min-1与293.15 K;A与B为各自输入谐波幅值,单位分别为m3·min-1和K;ωF为谐波频率,rad·min-1;φ为S(t)与T(t)之间的相位差。
3.2 建立最优化问题
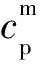
对同步操作时Δ3=f3(A,B,ωF,φ)含约束的最优化极值问题的表述如下:
定义周期操作的产物最大转换率δproducts,pmax,i,i=1,2,3,
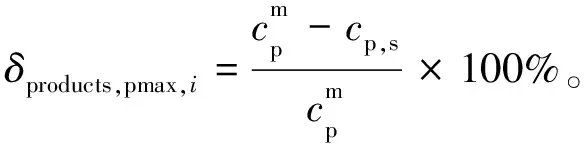
(19)
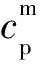
3.3 仿真条件设置
系统仿真应用中,每只狼都是问题的一个解。在提高产物产率的优化中,每只狼代表的产率反应为一组被优化的参数值。IGWO算法可以通过优化计算在众多反应物产率中找出一条最优产率所对应的参数值。同时为了保证生物柴油产率的稳定性与仿真的准确性,对仿真的时间进行了设置,选取时间范围为24×60 s。根据文献[19],优化技术不能保证找到精确的解决方案,所以本文提出将改进的灰狼算法的规模设置为50,每次运行最多100次迭代。并将其与GWO、DA、PSO和GA进行对比。
对式(17)和式(18)最优化极值问题进行周期操作生物柴油过程的参数优化,并且采样时间间隔设定为0.1 s。5种算法下各参数的选取见表1。
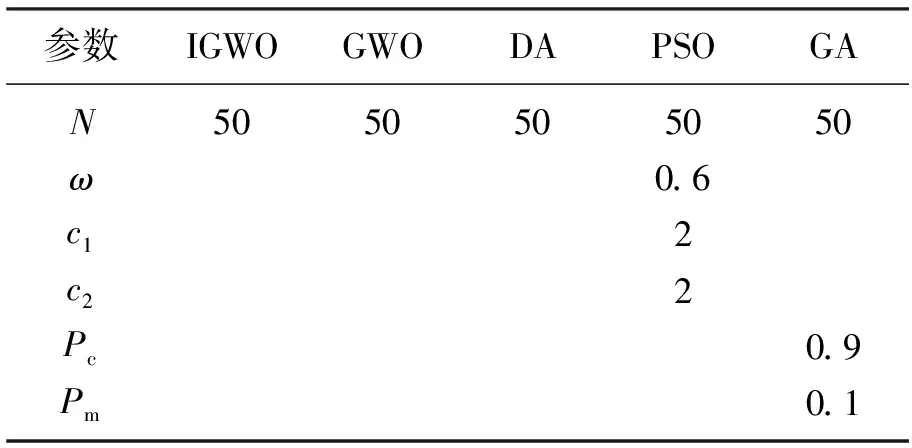
表1 各种算法的参数设置Table 1 Parameter settings of various algorithms
3.4 仿真结果
利用IGWO、GWO、PSO、GA、DA算法对选取的周期操作制取生物柴油的目标函数进行仿真,得到各个算法的适应度值变化曲线如图3~图5所示(见封2)。
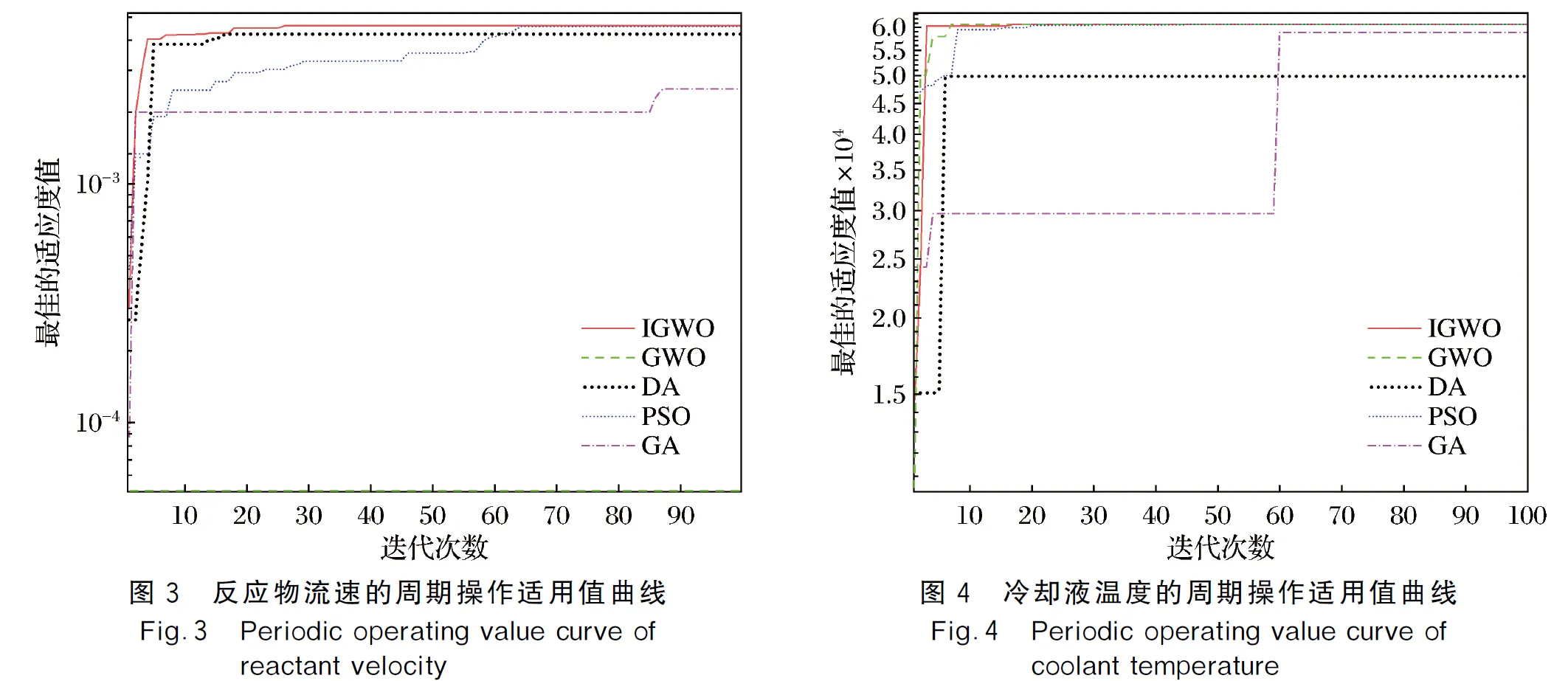
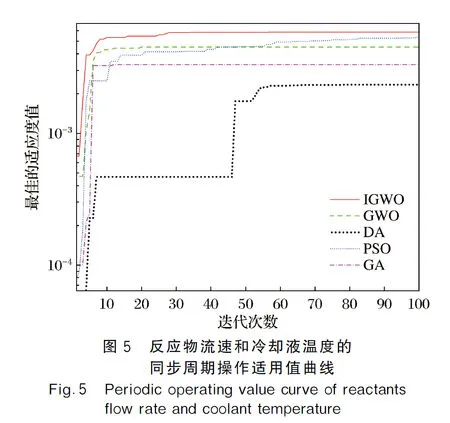
从各个适应度值变化曲线可以看出,IGWO算法无论在单步操作还是在同步操作上,其适应度曲线、上升速度、收敛代数以及最优的适应度都优于另外4种算法,并且变化幅度比较稳定,说明IGWO算法在收敛性与稳定性上具有明显优势。5种算法优化得到的参数值见表2。
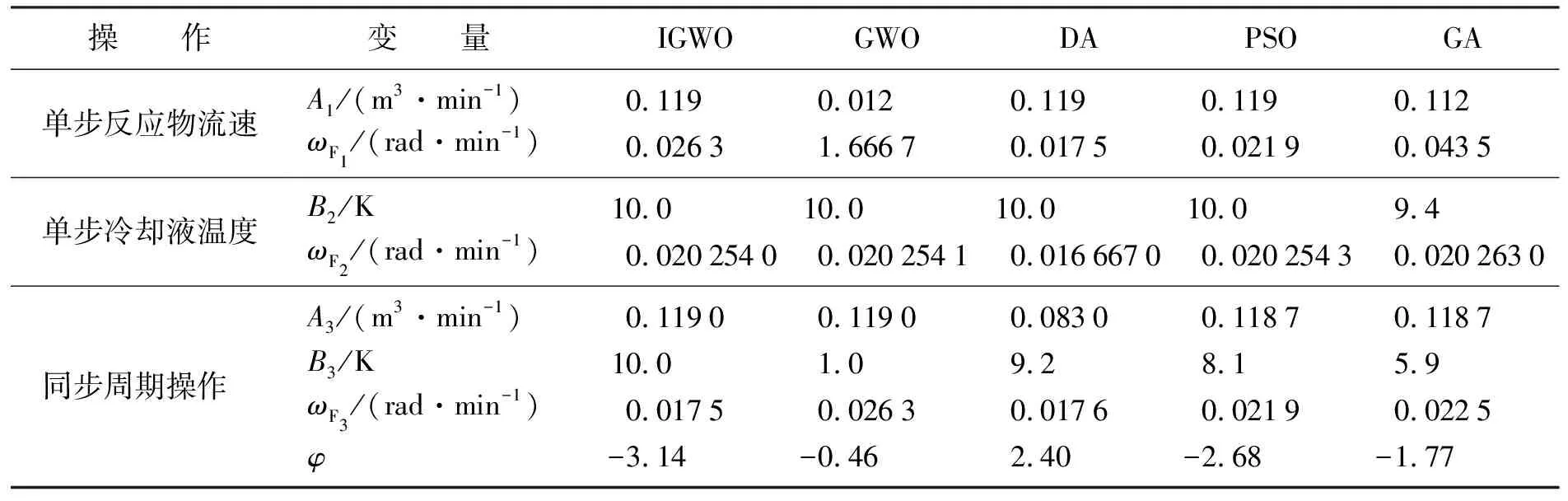
表2 各优化算法的参数值Table 2 Parameter values of each optimization algorithm
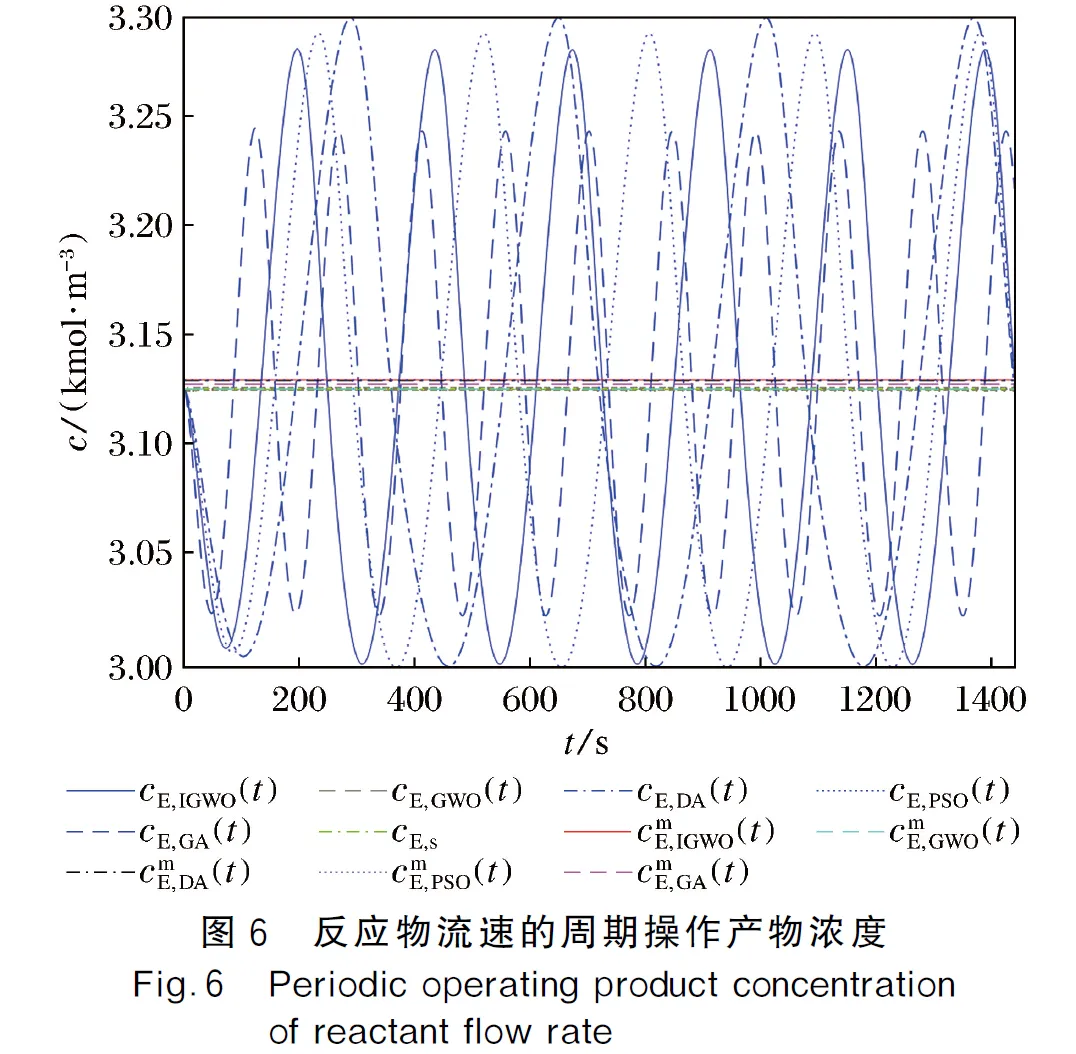
使用MATLAB R2019b对式(5)、式(6)模拟制取生物柴油进行仿真计算,稳态时的生物柴油产量为3.124 8 kmol·m-3,将表2中采用IGWO优化后的参数值带入仿真实验中可以得到生物柴油输出浓度的变化分别为如图6~图8所示(见封2),可以看出无论使用单步还是同步周期操作方式对生物柴油制取是有利的,能促进生物柴油的产率,并且使用IGWO算法优化的生物柴油输出浓度均高于另外4种算法,说明IGWO算法优化的效果最好。
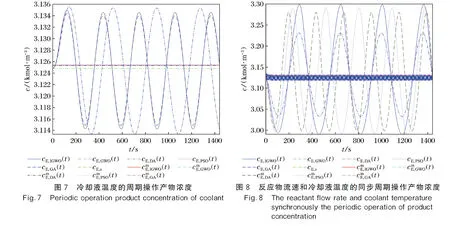
为了更加直观地观察优化后各自产物浓度的提升,在图9~图11(见封3)中忽略了周期操作时产物浓度时时周期性的变化,而保留了稳态操作浓度和各自算法优化后的出口浓度平均值。
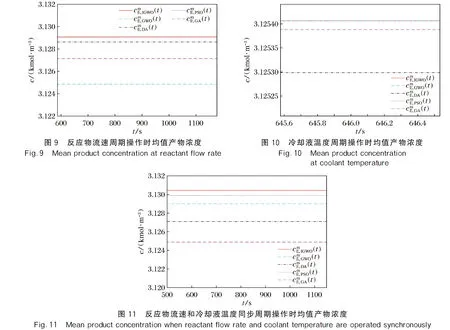
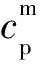
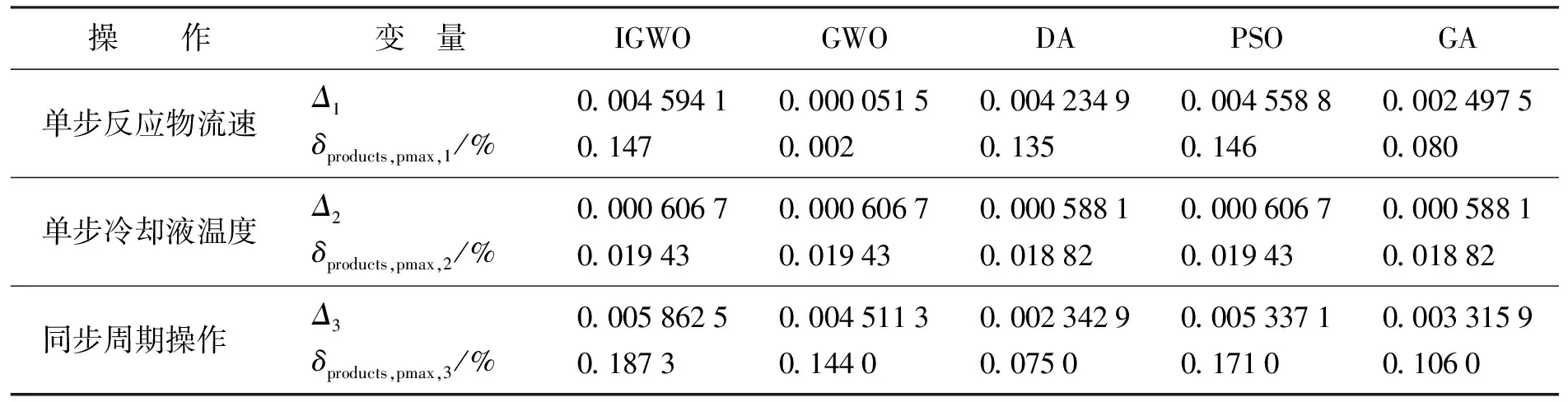
表3 各优化函数的物料浓度差与最大转换率Table 3 Material concentration difference and maximum conversion rate of each optimization function
4 结 论
本文首次提出了利用IGWO算法对周期操作生物柴油过程的参数进行优化,包括分别对反应物流速和冷却液温度的单步周期操作与同时对反应物流速和冷却液温度同步周期操作,不仅能够克服基于GWO、PSO、DA和GA的参数优化算法容易陷入局部最优的缺点,而且能够快速得到使产物浓度更优的参数,从而提高生物柴油的产物产率。从优化的适应度值,优化的物料浓度差与最大转换率说明IGWO对于复杂流程工业优化控制领域更加具有优势,能够获得更大的经济效益。
