火灾后方截面CFDST构件偏压机理分析

刘 晓, 刘思颖, 王 兵

(沈阳大学 建筑工程学院, 辽宁 沈阳 110044)

中空夹层钢管混凝土柱(CFDST)是把内外钢管同心放置,在两层钢管中间填充混凝土而形成的新型组合结构。CFDST结构不仅具有承载力高和延性好等优点,还具有更轻的自重、更大的抗弯刚度、良好的耐火性能等特点[1-4]。在各种灾害中,火灾发生最为频繁且危害性极强,所以提高建筑结构的抗火性能,确定合理的防火构造措施,改善建筑在火灾下和火灾后的工作性能,对人类安全、社会安定以及环境保护有重要意义。

目前对于CFDST抗火性能的研究主要集中在耐火极限和火灾后轴压力学性能方面,而关于火灾后CFDST偏压构件力学性能的研究较少。杨友福等[5]对火灾下CFDST的机械性能进行了试验,分析了CFDST火灾下残留负荷系数和影响部件耐火极限的各种因素;Lu等[6]进行火灾下自密实CFDST构件试验,证明了空心率对火灾下的耐火极限有显著影响,明确了钢管与混凝土之间的相互约束力能有效提高极限温度;以火灾受火时间为主要变量,余鑫等[7]研究认为火灾后构件的承载力显著下降,构件空心率在相同条件下,火灾后的剩余承载力最高的是方套圆截面的CFDST构件;Lu等[8]在之前试验的基础上,研究的关于火灾后自密实CFDST构件的理论表明,通过增加外钢管的厚度可以有效降低构件所经历的最高温度;刘晓等[9]利用有限元软件模拟分析高温后CFDST的轴压性能,研究空心率、温度和构件名义含钢率对构件火灾后剩余承载力影响的结果表明,随着构件空心率的增加、温度的上升及名义含钢率的减小,构件在火灾后剩余承载力逐渐下降。

在现代化建筑工程中,CFDST构件属于偏心受压构件,被广泛应用于高层建筑和桥墩等,但目前火灾后CFDST偏压力学性能研究较少。本文采用合理的本构关系模型,利用ABAQUS有限元软件,构建正确的火灾后CFDST偏心受压模型,分析不同变量对CFDST承载力的影响,深入研究方截面CFDST构件偏压工作机理。

1 有限元模型

1.1 材料的本构关系

考虑温度变化对混凝土的影响,核心混凝土选用林晓康[10]的本构关系(σ-ε)模型。高温后钢材内部结构发生变化,但冷却后其强度又有很大程度的恢复,高温后采用韩林海[11]提出的火灾后钢材本构关系(σ-ε)模型,具体表达式为

式中:fy为钢材的屈服强度;fy(θmax)为高温自然冷却后钢材的屈服强度;θmax为历史所遭受的最高温度。

1.2 模型建立

首先对方截面CFDST构件进行热力学分析,建立方截面CFDST的温度场分布,然后再加入力场进行力学分析。钢管在热分析中采用4节点壳单元DS4,在力学分析中采用8节点实体单元C3D8R;混凝土和盖板在热分析中采用实体单元DC3D8,在力学分析中采用壳单元S4。

设置热分析的边界条件时,忽略钢管和混凝土间的接触阻挡热量,只考虑柱与外部环境的热辐射和热对流,即认为热量可以完全传递。在力学分析中,设置盖板和混凝土之间采用硬接触传递力,内外钢管和盖板之间采用“shell to solid”约束方式,内外钢管与混凝土之间的界面模型采用法线方向的硬接触和切线方向的库伦摩擦接触,其中火灾后界面间的摩擦系数取0.25[12],在接触设置中遵循刚度大的面为主面,刚度较小的面为从面。网格的划分采用网格试验的方法选择合理的网格密度。边界条件定义为上端板加载线U1=U2=0,在Z方向上施加位移,下端板加载线U1=U2=U3=0,具体加载方式如图1所示。

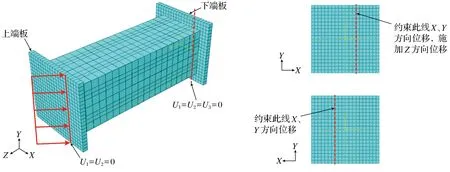
图1 火灾后偏心受压CFDST构件的边界条件Fig.1 Boundary conditions of eccentrically compressed CFDST after fire

1.3 模型验证

采用上述建模方法对文献[13-15]中的各偏压构件进行模拟,各文献构件的具体参数见表1。有限元模拟结果与试验结果的对比如表2所示,表中Nue、Nc分别为试验值和有限元模拟值,对数据处理计算得到有限元模拟的偏压极限承载力与各试验构件偏压极限承载力比值的标准差为0.061,说明本文所建立模型是正确的。

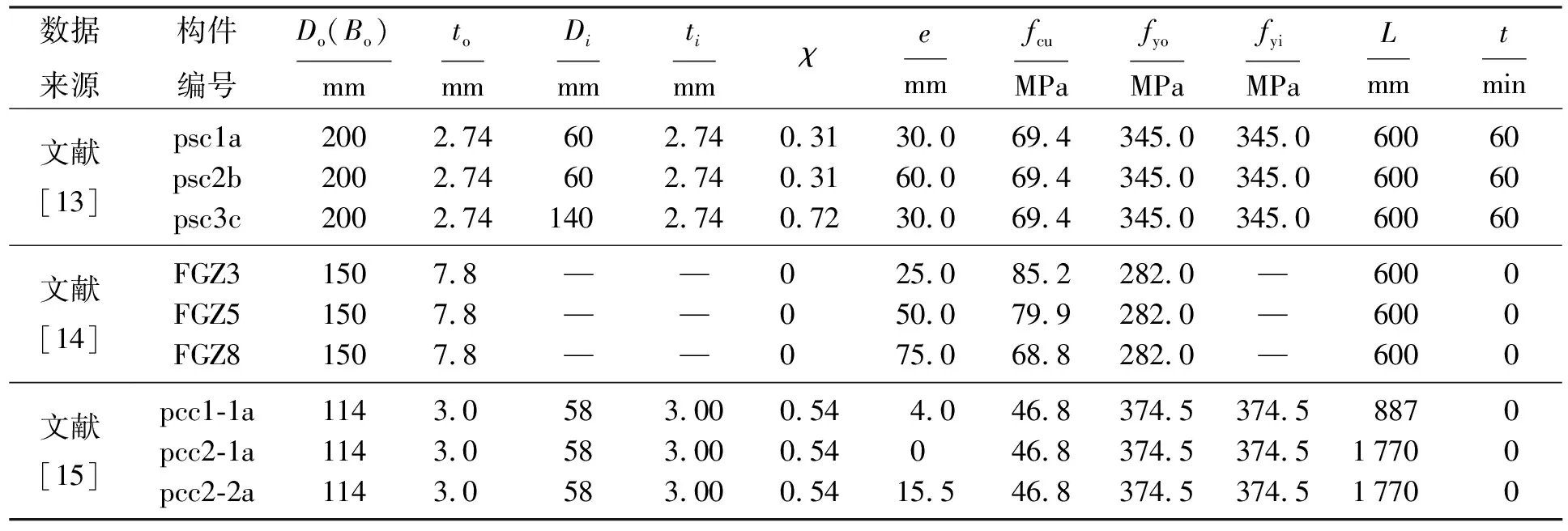
表1 试验构件参数Table 1 Parameters of test members

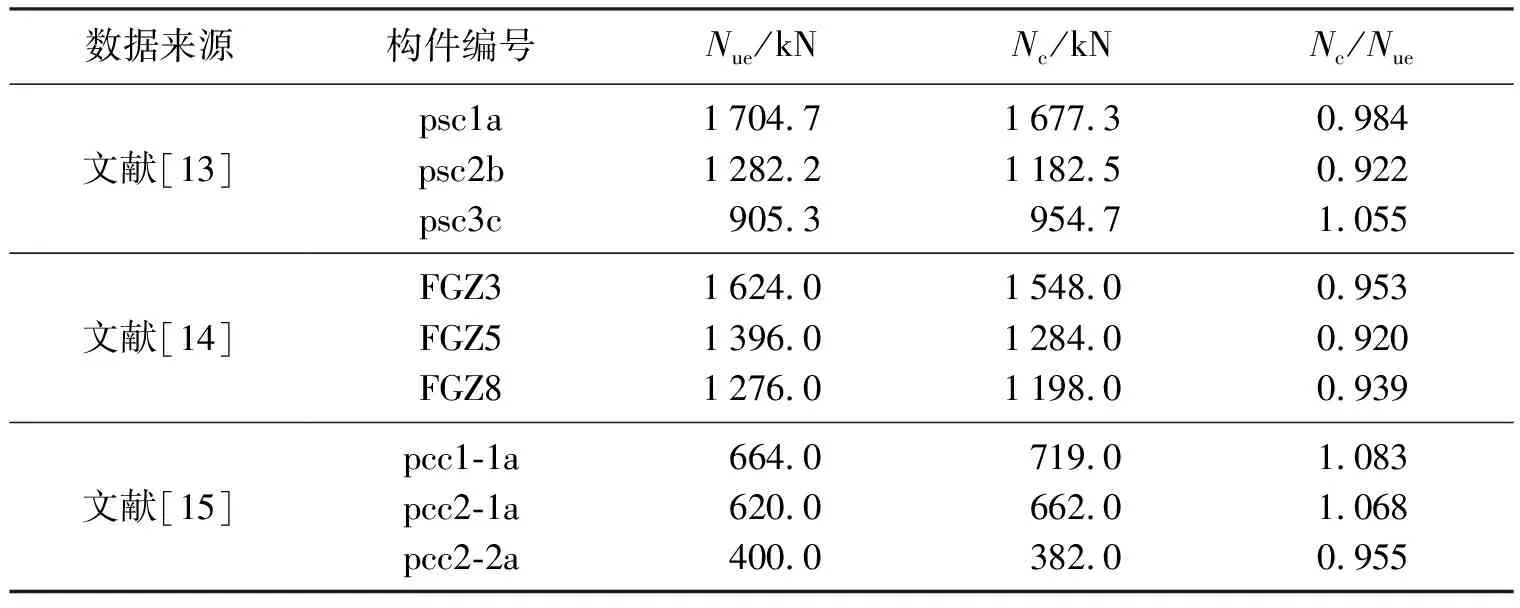
表2 有限元计算承载力与文献试验承载力对比Table 2 The comparison of bearing capacity between model results and literature test results

2 参数分析

使用ABAQUS有限元软件,基于正确的本构关系模型,将受火时间t(分别为0、60、120 min)、偏心距e(分别为15、30、45 mm)、空心率χ(分别为0、0.32、0.42、0.64)作为主要参数,共建立了18组方截面CFDST偏压模型构件,构件具体参数见表3。通过对比分析不同变量的构件得出各变量对火灾后方截面CFDST偏压构件载荷(N)-跨中挠度(um)关系曲线的影响规律。

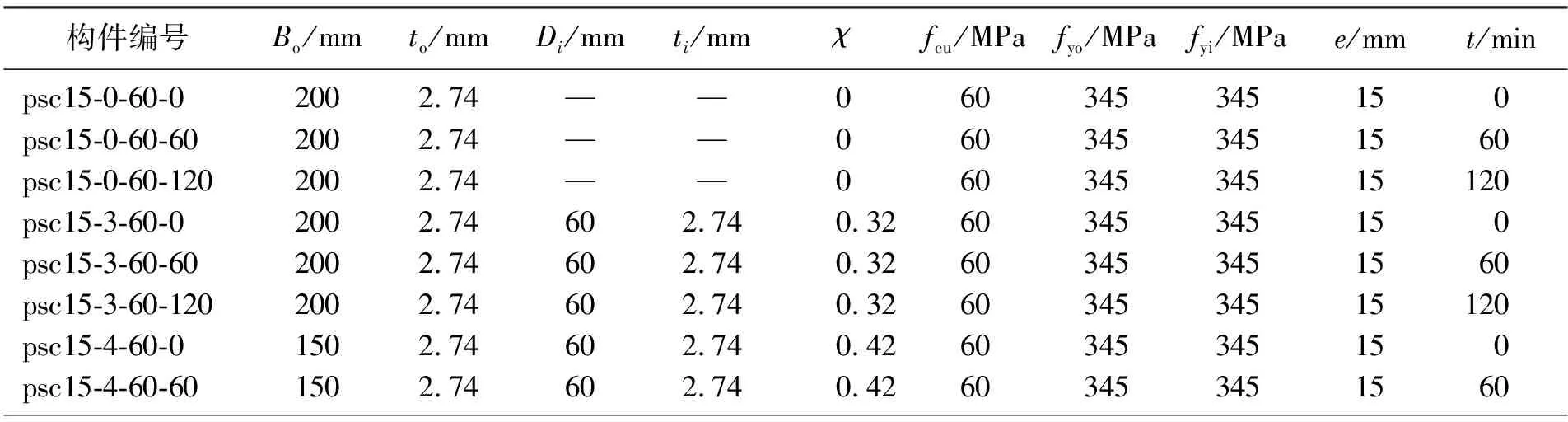
表3 有限元模型构件参数Table 3 Parameter list of finite element specimen

续表3

2.1 受火时间t

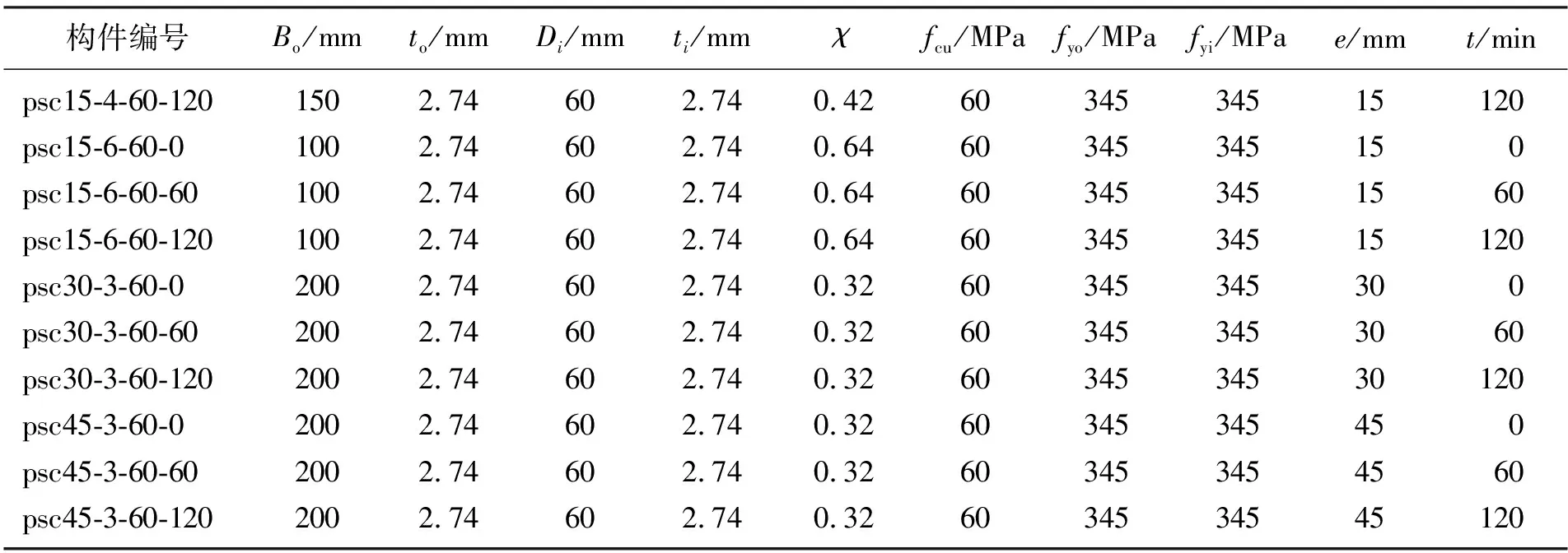
图2为偏心受压构件(偏心距e为15、30、45 mm)在不同受火时间时的N-um关系曲线,图2(a)中t=0、t=60和t=120 min所用的构件分别为psc15-3-60-0、psc15-3-60-60和psc15-3-60-120,图2(b)中t=0、t=60和t=120 min所用的构件分别为psc30-3-60-0、psc30-3-60-60和psc30-3-60-120,图2(c)中t=0、t=60和t=120 min所用的构件分别为psc45-3-60-0、psc45-3-60-60和psc45-3-60-120。由图2可知:相同偏心距下,构件受火时间增加,其偏压极限承载力均减小;构件达到极限承载力后,曲线下降趋势变缓,尤其在受火时间为60和120 min时,曲线不再有下降趋势,因此方截面CFDST构件在火灾后期也能表现出良好的延性。

(a) e=15mm(b) e=30mm(c) e=45mm

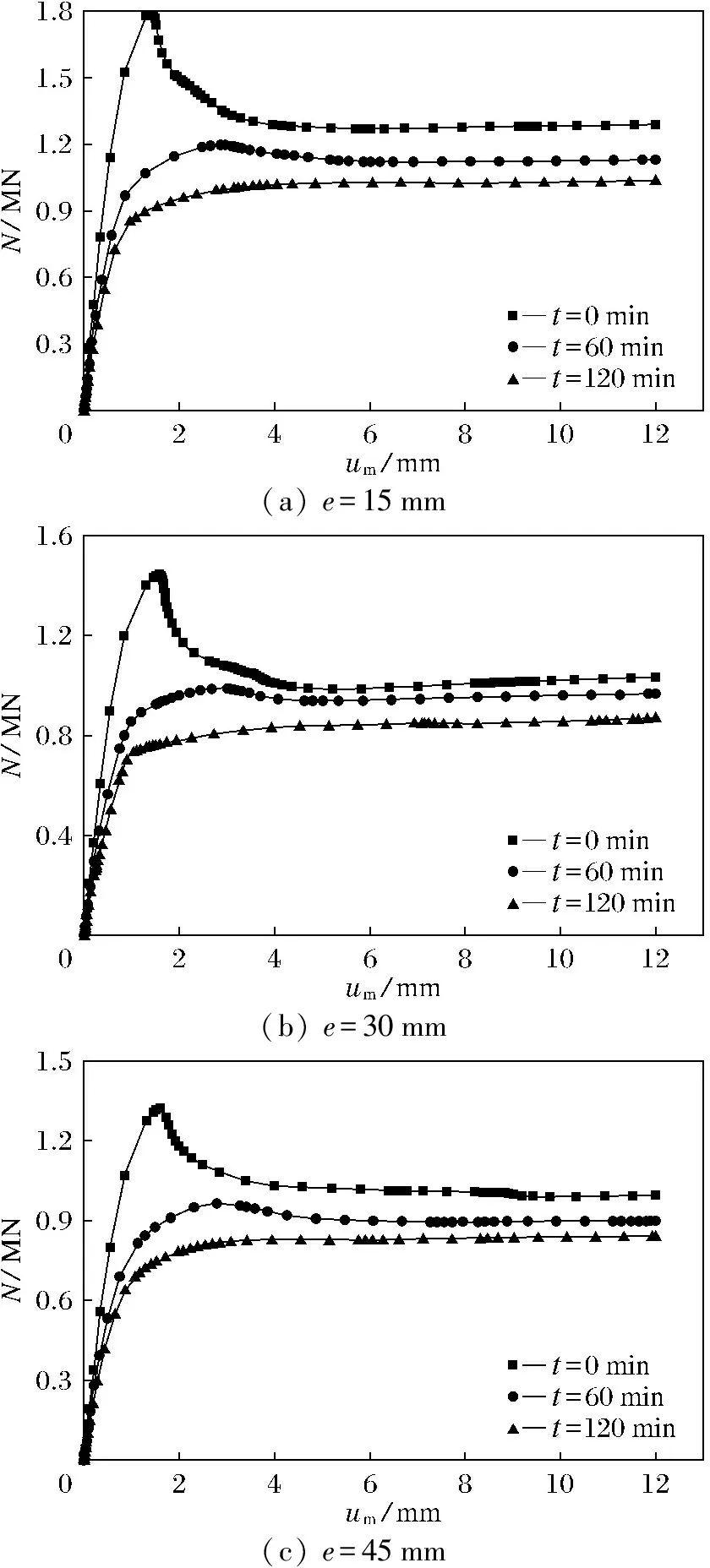
不同偏心距下构件的受火时间对承载力的影响对比情况如图3所示,由图3可知:受火时间60 min的构件承载力比受火时间0 min的极限承载力平均降低了31.61%;受火时间120 min的构件极限承载力比受火时间0 min的极限承载力平均降低了39.57%;受火时间120 min的构件极限承载力仅比受火时间60 min的极限承载力降低8.96%。构件极限承载力在受火时间不大于60 min时下降的幅度较大,受火时间60 min后下降的幅度较小。因为受火时间不超过60 min的情况下,方截面CFDST中的核心混凝土随受火时间的推移会产生温度裂纹,造成无法恢复的机械损失,所以随着受火时间的增加,承载力降低幅度会越来越大;受火时间超过60 min后,核心混凝土明显丧失了承载能力,此时钢材恢复了一部分力学性能,内外钢管开始分担载荷。因此,当受火时间超过60 min后,方截面CFDST承载力下降幅度逐渐减慢。

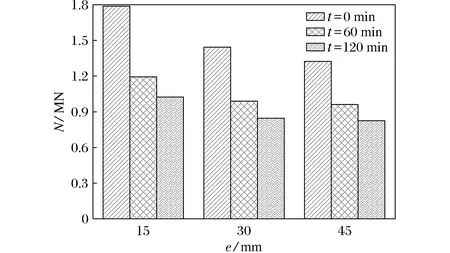
图3 不同偏心距下构件的受火时间对承载力的影响Fig.3 Influence of fire time on bearing capacity under different eccentricity

2.2 偏心距e

不同受火时间下的构件在偏心距不同时的N-um曲线如图4所示。由图4(a)可知:常温状态下,偏心距为45 mm的构件比偏心距为30 mm构件的极限承载力降低8.22%;偏心距为30 mm的构件比偏心距为15 mm构件的极限承载力降低19.35%。由图4(b)可知:受火时间为60 min时,偏心距为45 mm 的构件比偏心距为30 mm构件的极限承载力降低2.60%;偏心距为30 mm的构件极限承载力比偏心距为15 mm构件的极限承载力降低17.27%。由图4(c)可知: 受火时间为120 min时,偏心距为45 mm的构件比偏心距为30 mm构件的极限承载力降低3.37%;偏心距为30 mm的构件比偏心距为15 mm构件的极限承载力降低16.03%。由此可以看出,随着受火时间的增加,方截面CFDST偏压构件的极限承载力下降幅度并不大。

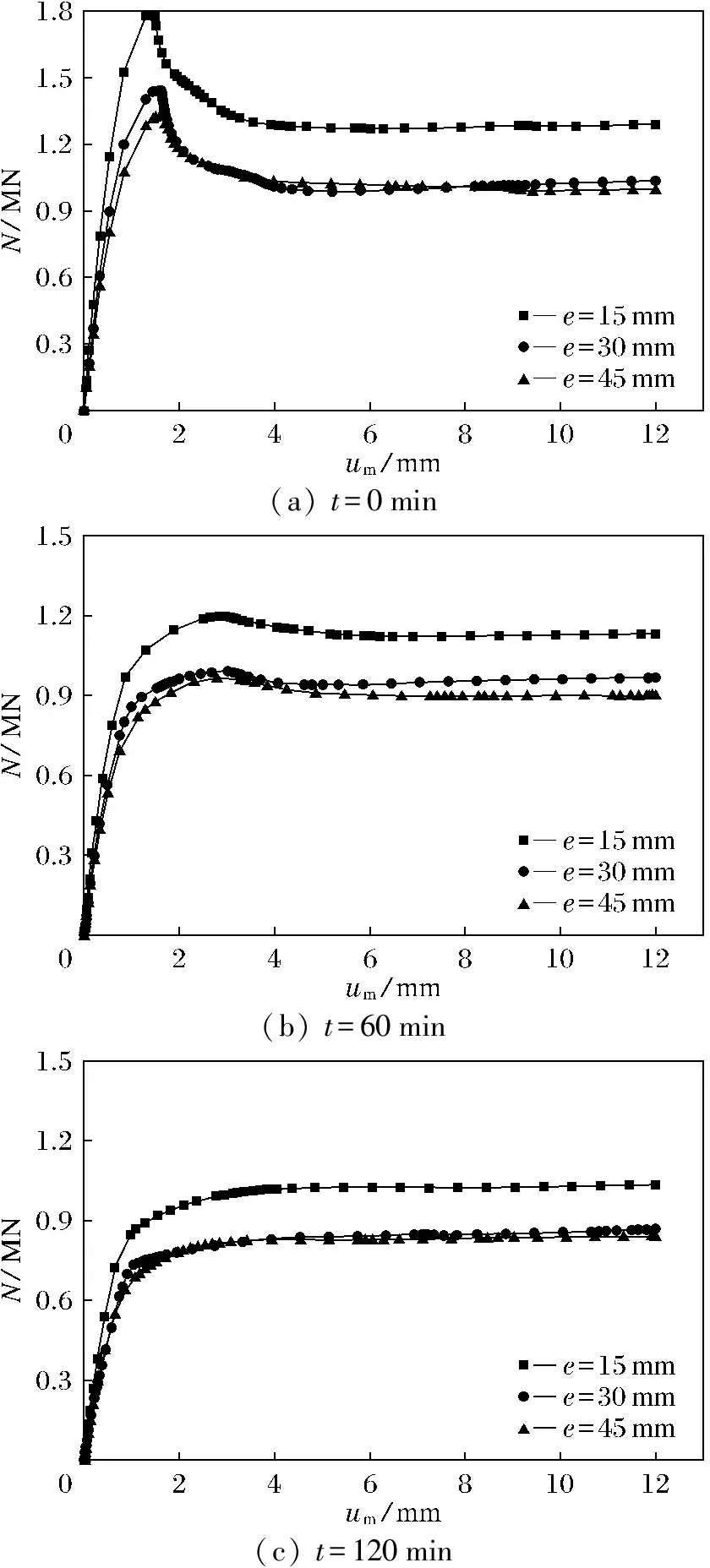
(a) t=0min(b) t=60min(c) t=120min

方截面CFDST偏压构件达到极限承载力后,随着偏心距的增加,N-um曲线变得平缓,表明其延性逐渐提高。这是因为在加载过程中,主要载荷由钢管承受,钢材的延性比混凝土好,并且构件偏心距越大,中和轴侵入内钢管距离就越大[15],所以方截面CFDST构件表现出良好的延性。

2.3 空心率χ

图5是不同受火时间的构件在不同空心率下的N-um关系曲线,图5(a)中χ=0、χ=0.32、χ=0.42和χ=0.64所用的构件分别为psc15-0-60-0、psc15-3-60-0、psc15-4-60-0和psc15-6-60-0,图5(b)中χ=0、χ=0.32、χ=0.42和χ=0.64所用的构件分别为psc15-0-60-60、psc15-3-60-60、psc15-4-60-60和psc15-6-60-60,图5(c)中χ=0、χ=0.32、χ=0.42和χ=0.64所用的构件分别为psc15-0-60-120、psc15-3-60-120、psc15-4-60-120和psc15-6-60-120。图6是不同偏心距构件的空心率对承载力的影响柱状图。总体上,随着构件空心率的增加,方截面CFDST构件承载力降低,其N-um关系曲线的下降段逐渐变缓,后期也未下降。这是因为随着空心率的增加,断面实际含钢率增加,钢材代替混凝土承担的负荷也逐渐增加。与混凝土相比,钢材具有更好的延展性,所以构件N-um关系曲线后期的下降段变得松弛,延展性变好。即随着空心率的有效增加,方截面CFDST构件延性相应增大。

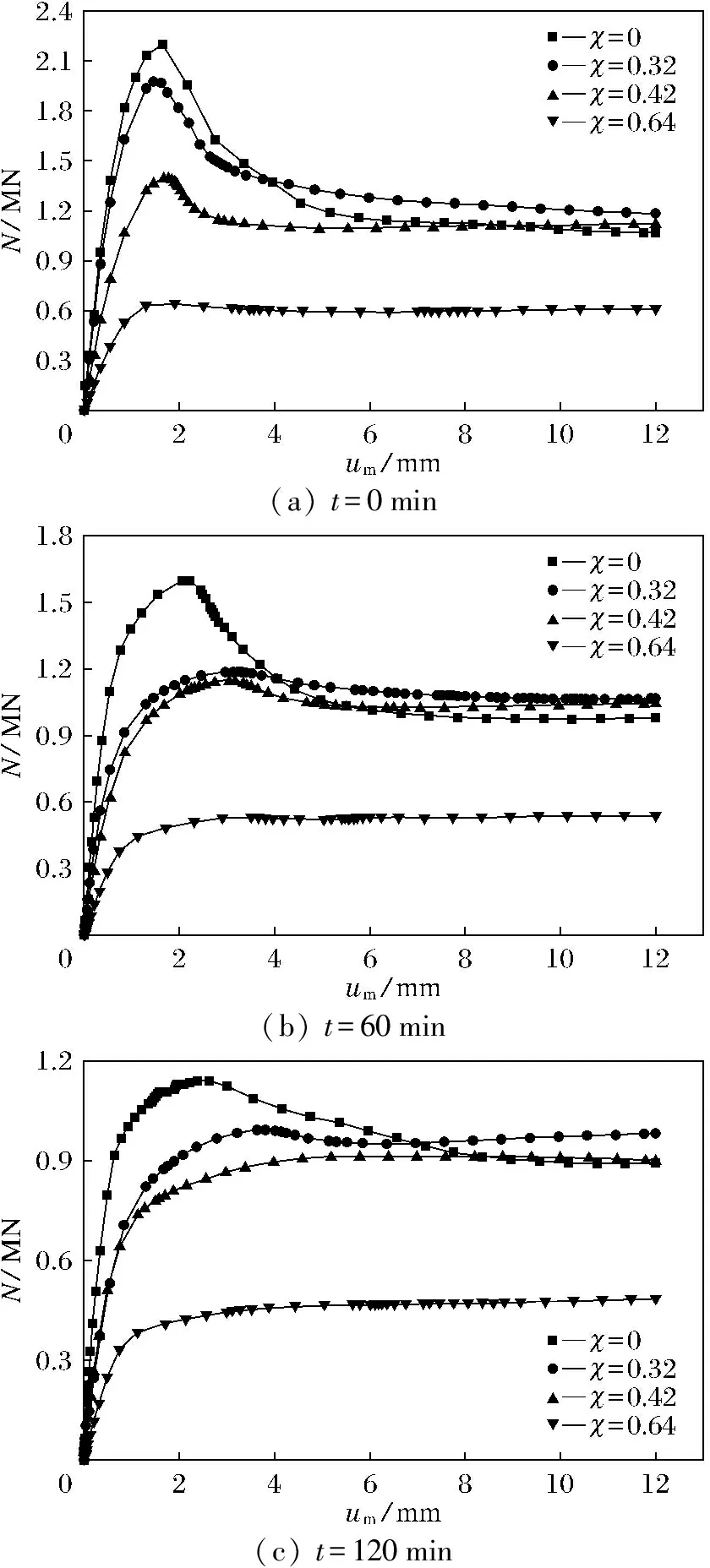
(a) t=0min(b) t=60min(c) t=120min

3 典型曲线分析

为了对火灾后方截面CFDST构件偏压工作机理进行分析,选取受火时间t=60 min、偏心距e=45 mm的方截面CFDST构件,对其典型载荷(N)-应变(ε)曲线进行分析。

图7为受火时间60 min时方截面CFDST偏心受压构件典型N-ε曲线。为了便于讨论,在曲线上取4个特征点,分别为点O、点A、点B、点C。点O为构件施加载荷的起点,点A为构件弹性阶段的终点,点B为构件达到极限承载力时对应的点,点C为构件纵向应变达到2×10-4的点。由图7可知整个方截面CFDST构件、混凝土、内钢管和外钢管随着应变的增加,各自承担载荷的变化情况。整体上看,受火时间t=60 min时方截面CFDST构件主要是由混凝土承担载荷,混凝土和外钢管分别占总承载力的44.96%和37.48%,占比最少的是内钢管,它所承担的载荷仅仅占17.56%。

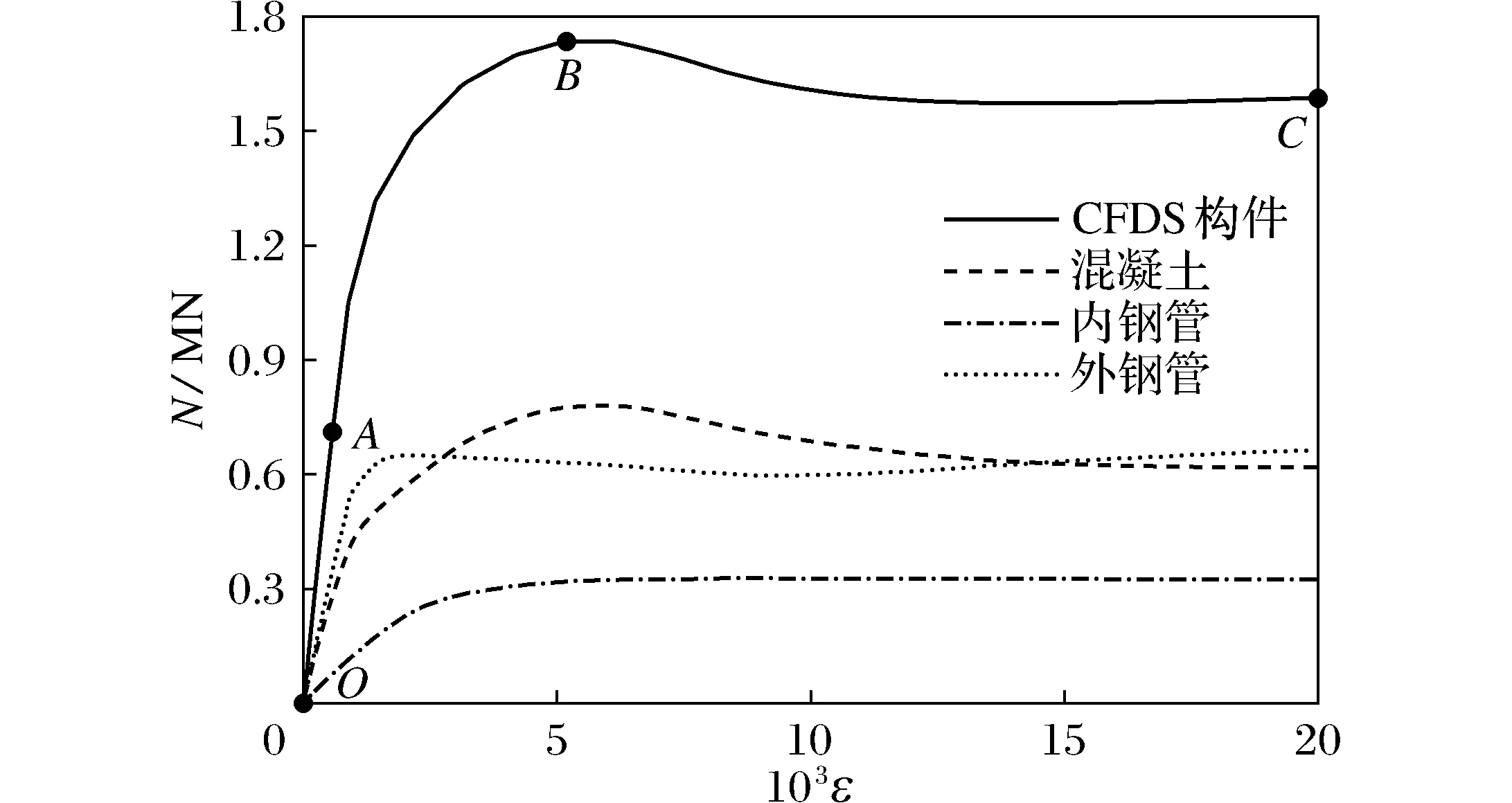
图7 典型方截面CFDST偏心受压构件N-ε曲线(t=60 min)Fig.7 Typical N-ε curve of square CFDST eccentric compression member(t=60 min)

图8为各特征点处的跨中截面混凝土纵向应力分布,图9为内、外钢管各特征点处应力分布。结合图8和图9得出:在点O时,构件中的混凝土和内外钢管的应力均为0,OA阶段是弹性阶段,基本是一条直线。构件承受偏载后,整个截面的压缩混凝土逐渐产生拉伸应力,最初的拉伸应力出现在外钢管附近,应力从远离偏心载荷的一侧逐渐增加到偏心载荷一侧,点A应力分布如图8(a)所示,此时,内外钢管处于弹性阶段,最大压应力出现在压区外缘,该阶段混凝土和内、外钢管独立工作;AB阶段属于弹塑性阶段,在这个阶段,混凝土开始开裂,拉伸面积逐渐增大,其特征是远侧拉伸,近侧压缩,中和轴移动进入内钢管,内钢管开始承担一部分力,然后承载力增加直到达到最大值,点B应力分布如图8(b)所示;在点C时,压区的混凝土被压碎,混凝土受拉区出现了很多条贯通的裂缝,然后逐渐退出工作,拉区混凝土的最大拉伸应力减少,内钢管也和混凝土脱离,内部钢管逐渐从全截面受压变为受拉,远离偏心载荷,内钢管负担主要的拉伸应力,承载力明显下降,点C应力分布如图8(c)所示。

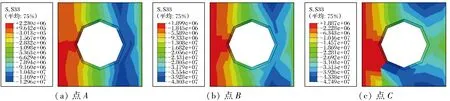
(a) 点A(b) 点B(c) 点C

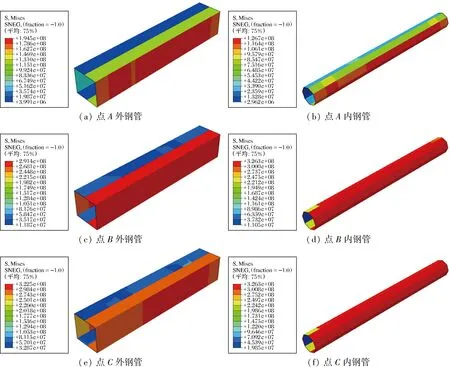
(a) 点A外钢管(b) 点A内钢管(c) 点B外钢管(d) 点B内钢管(e) 点C外钢管(f) 点C内钢管

4 结 论

1) 随着火灾受火时间的增加,构件达到偏压极限承载力后,载荷-挠度曲线的下降段逐渐变缓,说明火灾后方截面CFDST在后期表现出良好的延性;随着偏心距的增加,CFDST的承载力有小幅度下降;随着空心率的增加,方截面CFDST曲线下降段逐渐减慢,甚至不出现下降段,即方截面CFDST的延性随着空心率的增加而增加。

2) 当受火时间t=60 min时,方截面CFDST构件主要是由混凝土承担载荷,混凝土、外钢管及内钢管的承载力分别占总承载力的44.96%、37.48%和17.56%。