脊形前体俯仰动态绕流数值模拟研究

司芳芳，袁先旭，谢昱飞，刘福军，叶友达

(1.北京流体动力科学研究中心， 北京 100120； 2.中国空气动力研究与发展中心， 四川 绵阳 621000)

1 引言

随着空对空武器的发展，全方位射击成为可能，优先开火越来越重要[1]，这就需要飞行器具有较高的机动性和敏捷性，而这往往是通过飞机快速拉起到大攻角，甚至过失速来实现的。大攻角过失速机动是指战斗机在极短时间内实现姿态角大幅度的改变。要实现过失速机动，必须详细地了解大攻角下，静态和动态时飞行器空间流场及气动力特性。以往战斗机和导弹被限制进入大攻角状态，主要是因为机身、弹身这类细长体的绕流，在大攻角时会发生非对称乃至非定常分离，产生严重的横侧向气动力和力矩，从而导致飞机出现横/侧向偏离、机翼摇滚、下冲等复杂甚至不可控的飞行现象。

目前，先进战斗机如F-22和F-35均采用脊形前体，脊形前体主要由切拱弧和脊形边缘组成。脊形前体的背风流场的涡结构很强，且较稳定，该结构增加升力的同时也会对后面的机翼、垂直尾翼以及飞机头部等部件产生较强影响，进而影响飞机的操纵有效性[2]。较强的前体涡与机翼前缘涡相互干扰，常常能够延迟机翼的完全失速，增加最大升力，并能在有侧滑时提供稳定的滚转力矩，因此提高了飞机的横向稳定性[3]。脊形前体是一种兼具优良气动性能和隐身性能的构型，是当前和未来高机动飞行器设计可能采用的机身/弹身布局形式

经过国内外的大量研究，对脊形前体飞行器的静态气动特性[4～12]，已有较充分的认识，动态气动特性也有一定的研究。G.E.Erickson和J.M.Brandon[3]最早通过实验研究了单自由度、自由滚转运动对包括脊形前体的四种常规前体气动特性影响。Kenneth P.Iwanski和Robert C.Nelson[13-14]也研究了滚转运动对脊形和圆形前体气动力的影响。Tiger L.Jeans等[15-17]用DDES(delayed detached-eddy simulation)方法数值模拟研究了单自由度滚转对脊形前体和三角翼耦合的战斗机模型的气动力特性的影响。R.L.Mange[18-21]实验研究了脊形前体俯仰振荡运动时俯仰旋转点、减缩频率和雷诺数等参数的影响。

但由于常规风洞试验具有难以实现变来流马赫数、高角速率拉起以及在运动的同时进行测力等难点，且成本很高，对大攻角机动过程中流动演化机理和影响的研究尚不充分，因此，开展脊形前体快速、大振幅俯仰运动的数值模拟研究，掌握大攻角机动过程中涡结构演化和气动力迟滞效应，仍有着重要的工程应用价值和学术意义。

因此，针对脊形前体动态大攻角湍流大分离流动特点，采用基于SA(spalart allmaras)模型的IDDES(improved delayed detached-eddy simulation)混合模型，以及高效、高精度的动态非定常算法，开展了90°脊形角前体模型俯仰运动时的动态流场特性研究，与静动态数值模拟结果对比，分析动态流场的迟滞效应和动态气动力的非定常效应，并研究了来流马赫数对俯仰振荡动态涡流场结构和非定常气动力的影响。研究结果和结论可为先进高机动飞行器设计提供参考。

2 数值模拟方法

2.1 湍流模型

由于机动飞行时，动态流场结构可能跨越附着流动、分离涡流动、涡破裂流动和完全分离流动等具有显著差异的流态特征，气动力和力矩会呈现强烈的非定常、非线性特征，综合目前各种湍流方法的优缺点，为确保模拟结果能准确地反映流场结构和气动力非线性特性，采用基于SA的IDDES方法[22]，该方法结合了DDES和WMLES(wall-modeled large eddy simulation)方法，可有效解决DDES方法中存在的对数层不匹配的问题，并节省计算量。

WMLES模型通过长度尺度耦合雷诺平均Navier Stokes(RANS)模型和LES(large eddy simulation)模型，主要用于非定常和有湍流的流动中，长度尺度定义为

lWMLES=fB(1+fe)lRANS+(1-fB)lLES

式中:混合函数fB从0～1变化时，模型快速的从LES模式(fB=0)过渡到RANS模式(fB=1.0)。混合函数fe用于修正RANS和LES交界面相互作用而损耗过多的雷诺应力。

相对于通常的LES和(D)DES(detached-eddy simulation)，IDDES 采用了与网格大小和壁面距离皆有关的新的亚格子尺度，可实现湍流求解模型的转换。IDDES方法的长度尺度可以定义为

其中:νt为涡粘性，dw为到壁面的距离，κ为冯卡门常数，Ui， j为速度梯度。

2.2 数值计算方法

数值模拟中为了保证非定常的时间计算精度，同时又具有较高的计算效率，非定常时间推进采用双时间步隐式迭代法；无粘项的空间离散都采用迎风型NND格式。对于文中采用的IDDES混合湍流模型和相匹配非定常算法，课题组成员已通过大量典型算例进行了考核和验证，图1给出了三维NACA0015翼型强迫俯仰振荡的数值模拟结果与实验结果[23]的比较。从图1中可以看出：采用IDDES方法得到的计算结果在升力、阻力和俯仰力矩系数上与实验更接近，能准确地模拟到翼型上表面的非定常涡脱落现象，反映了从最大攻角下行时阻力和俯仰力矩的阶跃性突变。IDDES对于深失速分离流动特征结构有着更好的捕捉能力，对于动态强非定常流动的适用性和可靠性更好。其他算例验证结果参见文献[24-27]。

图1 升力、阻力和俯仰力矩系数迟滞曲线

2.3 研究模型和计算网格

选用的90°脊形角的前体模型是参考R.M.Hall的实验模型[13]，最大半展宽bmax为38.1 mm，全长为L=133.35 mm。图2给出了根据数据点拟合出来的前体横截面模型与实验模型外形数据。图3为计算模型三视图。

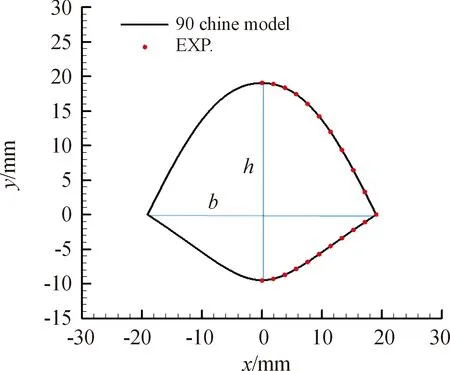
图2 计算模型横截面与实验模型外形数据图

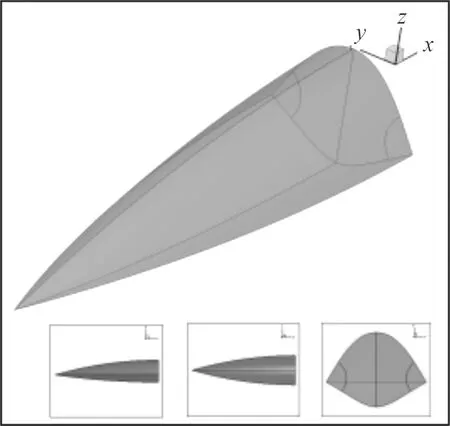
图3 脊形前体计算模型图

模型宽度b、高度h与体长x的关系式为

针对所研究的飞行器的运动的规律，采用刚性动网格技术来生成不同瞬时攻角下的动网格。以飞机的顶点为坐标原点，以静态时机体坐标轴的反向为x轴，y轴向上，z轴和x、y轴构成右手系，当物体绕其俯仰旋转轴发生θ角位移时，则：形成新网格系统的网格点坐标与静态网格系统的网格点坐标满足下面的关系式：

其中：下标s和d分别表示静态网格坐标和动态网格坐标，(x0，y0，z0)为俯仰旋转轴坐标。

文献[27]考察了网格疏密度对脊形角7.5°的前体模型计算结果的影响，为了满足IDDES对网格质量的要求，给出较为准确的空间涡结构图，且综合考虑计算效率，文中前体模型的网格参照脊形角7.5°的前体模型的G2网格的规模，采用C-H型网格，网格规模为820万，沿流向、法向和展向分布为231×181×91，其中前体上沿流线分布141个点。所有网格都在壁面附近加密，物面法向第一层网格间距为1×10-4mm，确保y+<10，计算网格如图4所示。

图4 计算网格示意图

1.4 计算条件

本文中主要开展俯仰振荡时脊形前体动态涡流场结构和非定常气动力特性的影响规律研究。取海拔0 km的大气参数，T∞=288.16，a∞=340 m/s，参考长度Lref=38.1 mm，力矩俯仰点Xm=88.01 mm，无量纲时间步长Δt=0.01。

来流不变，脊形前体绕机体坐标轴做俯仰运动。强迫俯仰振荡定义为攻角随时间以正弦函数变化：

α(t)=Am+A0sin(2kt)

式中：Am为平均攻角，A0为振动幅值，k为减缩频率，定义为

其中f为俯仰振荡频率。

取来流Ma=0.2、0.4、0.8，f=2.5 Hz，Am=30°，A0=30°。

3 数值结果

3.1 随攻角变化规律

俯仰运动是高机动飞行器典型的简化模拟机动动作。研究了Ma=0.4时脊形前体模型俯仰振荡时气动力特性以及相应的空间流场，并与静态时分析比较。

图5为前体强迫俯仰时气动力系数与静态时的气动力系数曲线。从图5中可以看出：

1) 升力系数随攻角的变化。α<10°时，俯仰振荡时CL与静态时基本一致；上仰过程中，10°<α<60°时，俯仰振荡时CL比静态时大；α=60°时，俯仰振荡时CL与静态时趋于一致；下俯过程中，30°<α<60°时，CL比上仰时明显偏小，α<30°时趋于一致。

2) 阻力系数随攻角的变化。α<30°时，俯仰振荡时CD比静态时略微偏大；α>30°时，上仰过程中CD比静态时偏大；α=60°时，俯仰振荡时CD与静态时趋于一致；下俯过程中，α>30°时，CD比上仰时明显偏小，α<30°时趋于一致。

3) 俯仰力矩系数随攻角的变化。α<30°时，俯仰振荡时Cm与静态时基本一致；上仰过程中，30°<α<60°时，俯仰振荡时Cm比静态时大；下俯过程中，40°<α<60°时，Cm比上仰时明显偏小，α<40°时趋于一致。

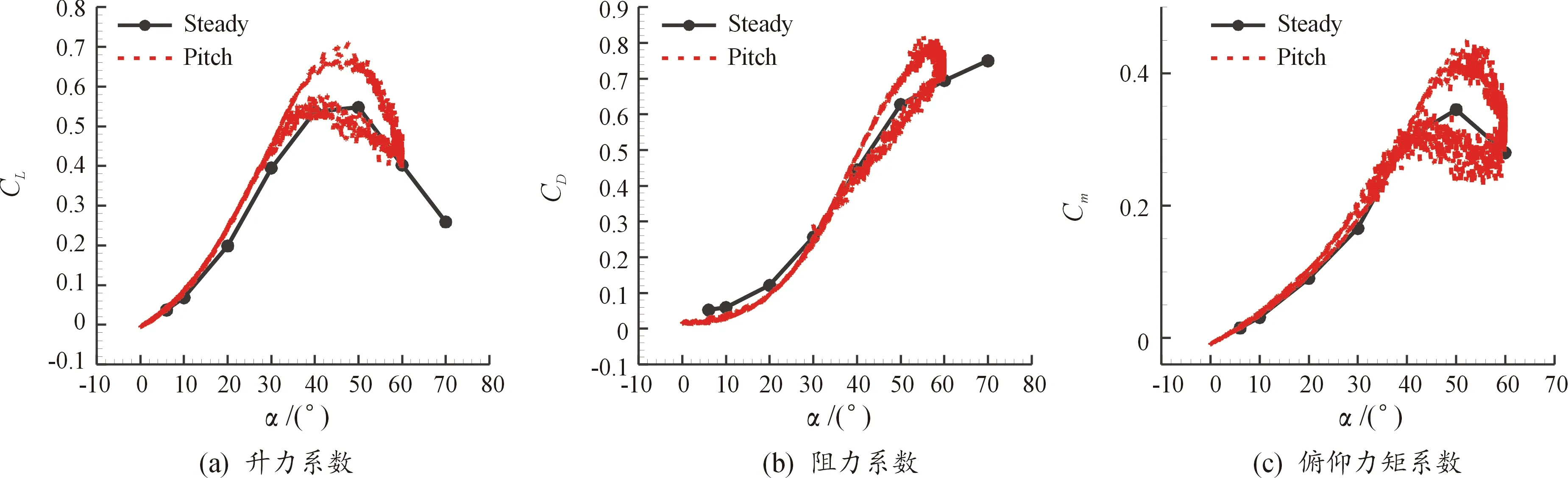
图5 俯仰振荡时气动力系数与静态时的气动力系数曲线

图6为俯仰振荡过程中典型攻角空间流线和总压损失云图。从图6中可以看出：上仰时前体涡的空间结构、二次涡和三次涡的产生、涡破裂等主要流场特征与静态时相似。但α=20°，上仰时，前体涡比静态时更贴近机身壁面，产生明显的二次涡和三次涡，而静态时没有三次涡的产生；下俯时的空间涡结构与上仰时趋于一致，但前体涡比上仰和静态时远离机身壁面。α=40°，上仰时三次涡破裂，而静态时三次涡没有破裂；下俯时前体涡、二次涡再附，与上仰时相比，破裂点更靠近机头顶点，没有三次涡的产生。α=50°，上仰时前体主涡、二次涡和三次涡破裂延迟，出现明显的非对称；下俯时前体涡没有再附，涡完全破裂。α=60°，静态和俯仰振荡时前体涡都完全破裂。

这表明小攻角时，俯仰振荡时流场与静态流场趋于一致，相应气动力系数差别很小；随着攻角增加，上仰时前体涡更贴近机身壁面，流场二次涡、三次涡产生的临界攻角减小，且动态运动效应使得前体涡破裂延迟，因此，在30°<α<60°范围内上仰时CL、Cm值较大。下俯过程中，由于涡破裂的历史效应，α>30°时，前体涡再附延迟，且远离机身背风面，导致CL、Cm比上仰时小，出现迟滞环；α<30°时，前体主涡、二次涡、三次涡完成再附，同一攻角下俯流场与上仰、静态流场结构趋同，导致气动力系数与静态时基本一致，气动力迟滞效应不明显。

3.2 马赫数影响

马赫数是一个重要的来流影响参数。研究了Ma=0.2、0.4、0.8时脊形前体模型俯仰振荡时气动力特性以及相应的空间流场。

图7为前体强迫俯仰时马赫数变化对气动力系数影响。从图7中可以看出：上仰过程中，α<40°时，CL、Cm随马赫数变化较小；α>40°时，随马赫数增加，CL、Cm变小；整个上仰过程中，马赫数变化时CD变化很小。下俯过程中，α>20°时，随马赫数增加，CL、CD、Cm变大；α<20°时，随马赫数变化CL、CD、Cm又趋于一致。随马赫数增加，CL、CD、Cm的迟滞环变小，压缩性效应增强，可抑制大攻角气动力脉动幅值，使得脊形前体纵向稳定性增加。

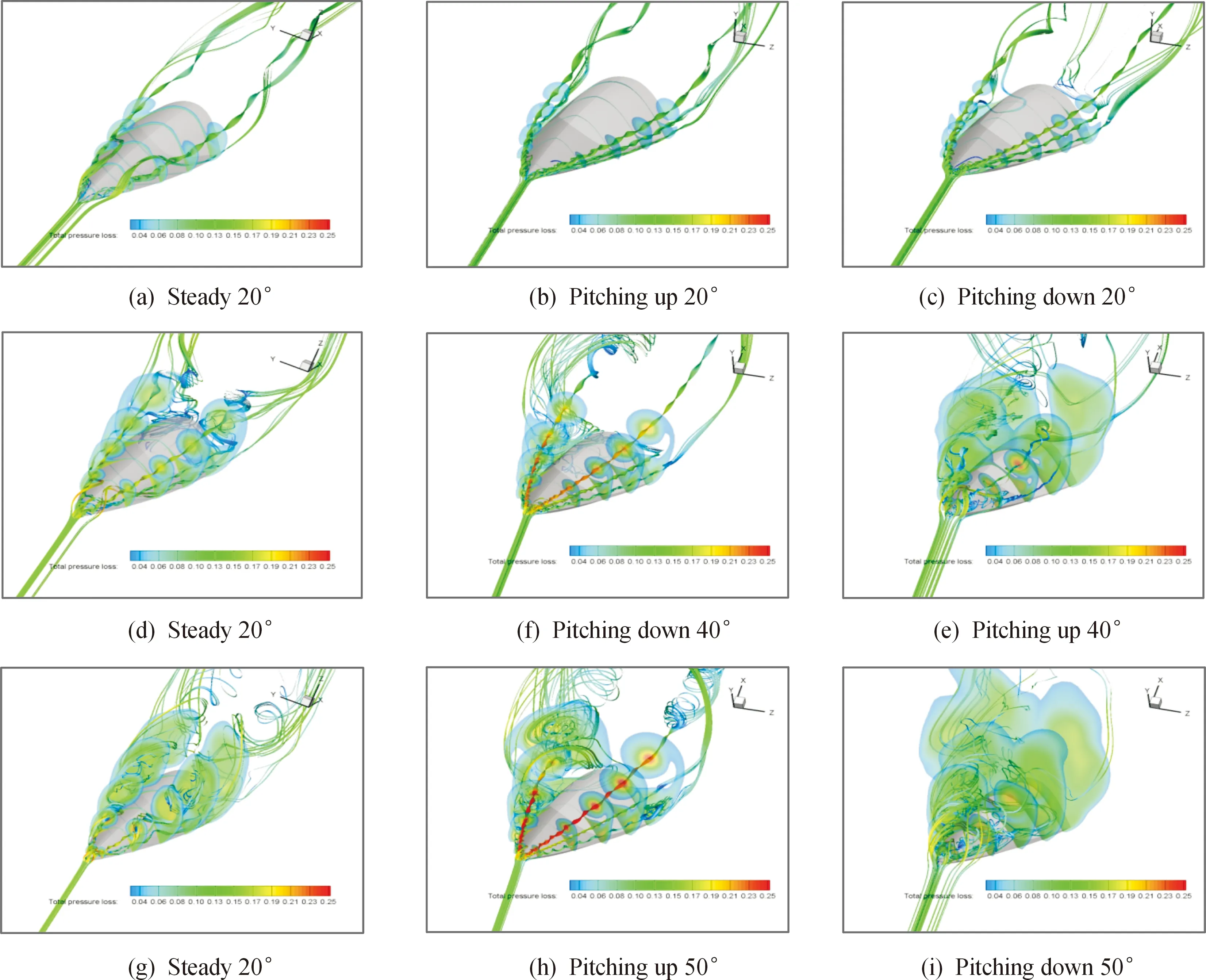
图6 俯仰振荡时空间流线和截面总压损失云图

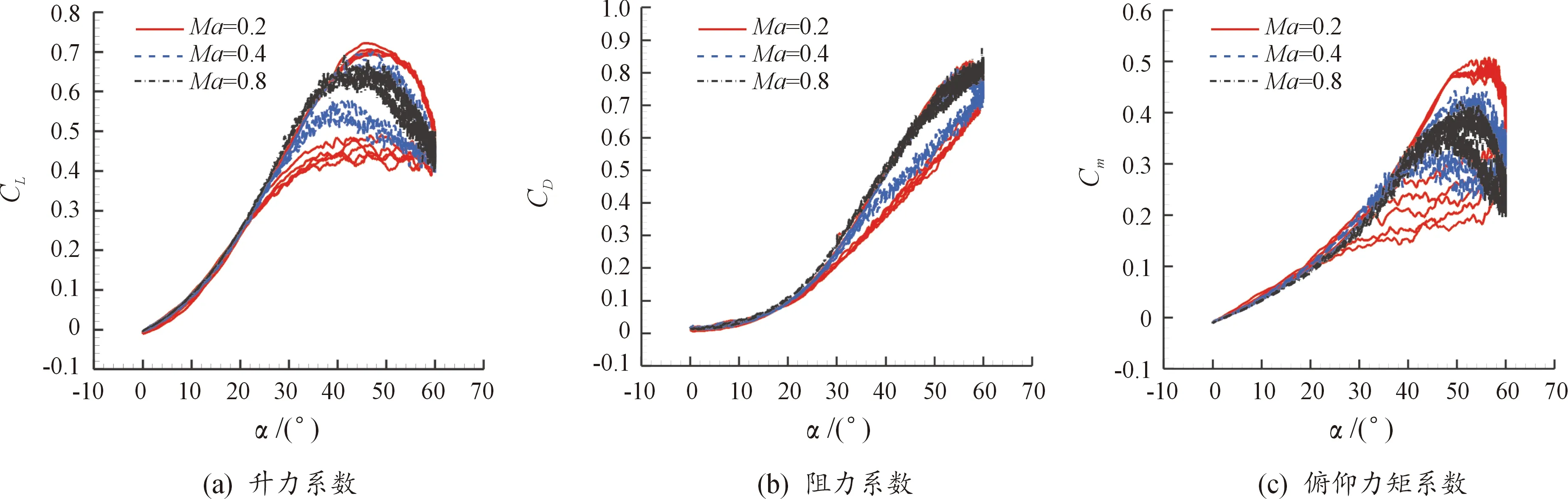
图7 不同马赫数时气动力系数曲线

图8、图9为强迫俯仰振荡时典型攻角的空间流线和截面总压损失云图，对比Ma=0.4时典型攻角的空间流线和截面总压损失云图可以看出：

上仰过程中，α<40°时，马赫数变化对空间流场结构影响较小；α=50°时，马赫数越大，前体远离机身壁面，涡破裂点越靠近机头顶点。下俯过程中，α=20°，Ma=0.2时前体主涡再附，主涡远离机身壁面；而Ma=0.4、0.8时前体涡完成再附，Ma=0.8时上仰和下俯流场基本一致，Ma=0.4时下俯流场前体涡比上仰时离背风面较远。α=40°，Ma=0.2时前体涡没有再附；Ma=0.4时前体主涡再附；Ma=0.8时前体主涡、二次涡、三次涡完成再附，与上仰时相比，涡破裂点前移。α=50°，Ma=0.8时前体涡再附，而Ma=0.4和Ma=0.8时前体涡没有再附。这表明，在亚声速范围内，上仰过程中，中小攻角时，马赫数变化对脊形前体空间结构影响很小，相应对气动力系数影响较小；随着攻角增加，α>40°时，马赫数越小，前体涡破裂延迟，相应的CL、Cm越大。下俯时，马赫数越小，前体涡的再附过程越缓慢，前体涡远离机身壁面，相应的CL、Cm越小。

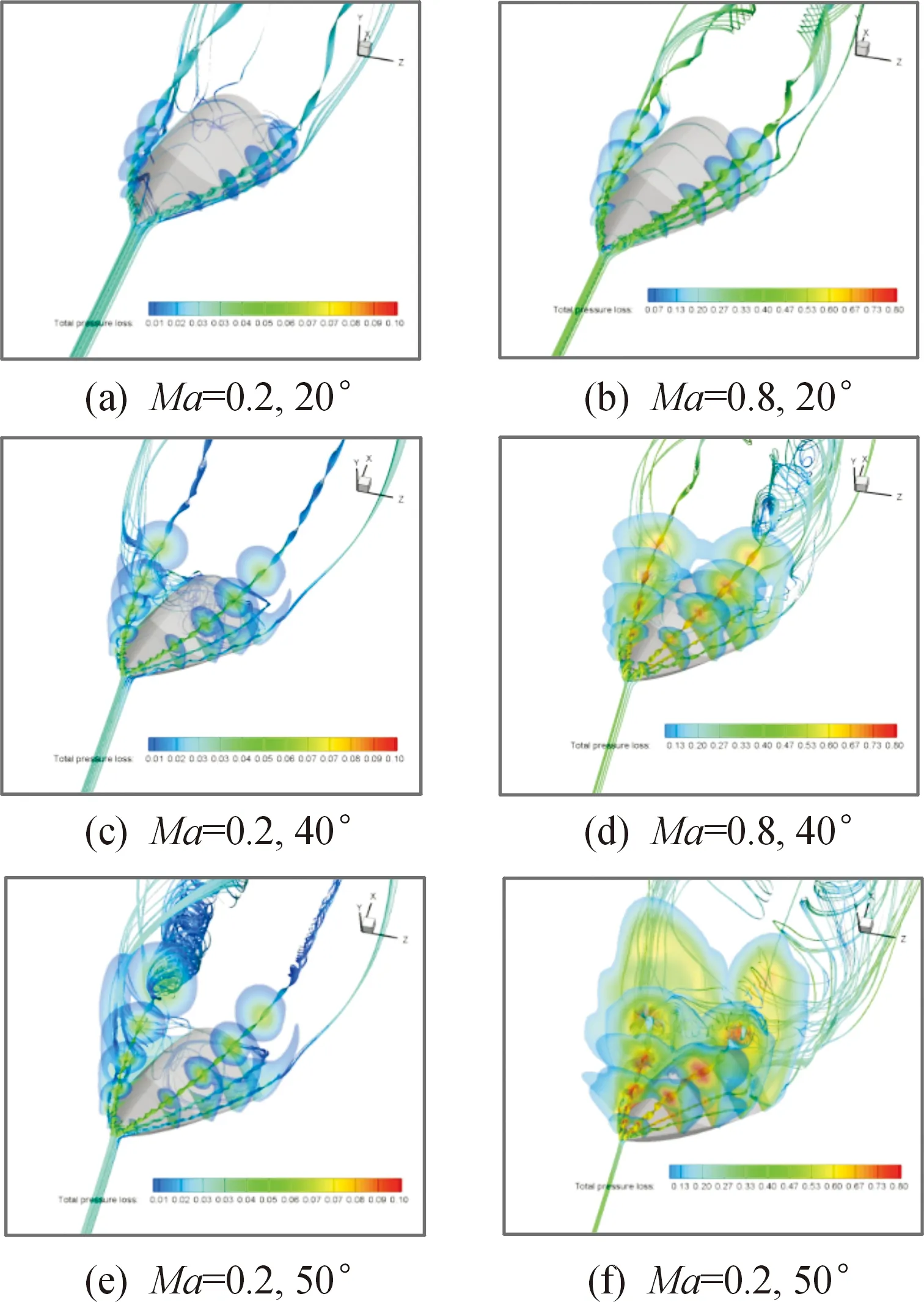
图8 上仰时空间流线和截面总压损失云图

图9 下俯时空间流线和截面总压损失云图

4 结论

在亚声速范围内，对于大振幅俯仰振荡运动，上仰和下俯动态运动效应对流场结构的影响差别显著，相应地，非定常气动力迟滞效应显著。上仰时，相较于静态而言，脊形前体动态运动效应使得二次涡和三次涡产生的临界攻角减小，主涡破裂延迟，导致大攻角时升力、俯仰力矩明显大于相应攻角的静态值。下俯时，由于涡破裂的历史效应，在α>30°时，前体涡再附延迟，且远离机身壁面，导致升力、阻力、俯仰力矩比上仰时小，出现迟滞环；当α<30°时，前体涡完成再附，同一攻角下俯流场与上仰、静态流场结构趋同，导致气动力系数与静态时基本一致，气动力迟滞效应不明显。马赫数效应表现为，马赫数越小，俯仰振荡的迟滞效应越显著。