用非惯性系中的角动量定理分析飓风球的运动

陈影，张艳燕，马晓栋

（新疆师范大学 物理与电子工程学院，新疆 乌鲁木齐 830054）

国际青年物理学家锦标赛（International Young Physicists′Tournament,简称IYPT）是全球最有影响力的年度物理学竞赛之一，比赛组织者每年为IYPT选定17个题目，与考试不同，这些题目是开放性的，没有标准答案。学生们研究IYPT 题目，就解决题目中物理问题的基本知识、理论分析、实验方案、结果讨论等进行辩论性比赛。在解决IYPT题目的过程中，将体会科学研究的思维方式和处理问题的方法，能够学到很多新知识，学习如何应用新知识，这些知识与通常课程中的有所不同。

IYPT 题目也可以用于地区性的和全国性的比赛，中国大学生物理学术竞赛（China Undergraduate Phys⁃ics Tournament，简称CUPT）是借鉴IYPT 的模式创办的面向全国所有高校本科生的层次最高、规模最大的辩论性物理学术赛事。

文章研究2019 年第32 届IYPT 的第六题，其内容为：通过起始时用手旋转，并使用一根管子（如吸管）朝其吹气，连在一起的两个钢球能以极高频率旋转，解释并探究这一现象。上述飓风球运动，是一个复杂而有趣的现象，两个刚性连接在一起的钢球，开始在地面绕过其质心的竖直轴旋转，在旋转频率增大到一定值时，其中一个钢球翘起，脱离与地面的接触，当翘起的角度达到一定值时，翘起的角度不变，两个连在一起的钢球整体进行稳定的进动，做类似陀螺的运动。

由于题目复杂，目前文献［1-2］分别用自由旋转对称体潘索理论和拉格朗日方程对飓风球的进动进行了定量分析，但它们对飓风球翘起原因的分析都是简单和定性的。文章推导非惯性系中的角动量定理，应用其定量分析飓风球的运动，既包括飓风球翘起的原因也包括飓风球的进动。

1 非惯性系中质点组角动量定理的推导

因为刚体可以看作是由质点组成的，所以上述角动量定理可以用来研究刚体的运动，以下用上述非惯性系中的角动量定理（3）和（4）来分析飓风球的运动。

2 飓风球地面转动状态的分析

用管子向飓风球吹气，由于吹气不均匀，对飓风球左边和右边施加的力大小不相等，使飓风球绕如图1所示过飓风球质心的竖直轴公转，设其角速度为同样由于吹气不均匀，对飓风球上部和下部施加的力大小也不相等，使飓风球绕如图1 所示过两球质心的轴自转，设其角速度为。其中，图1-2 是飓风球相对图1-1公转180度后的情况。

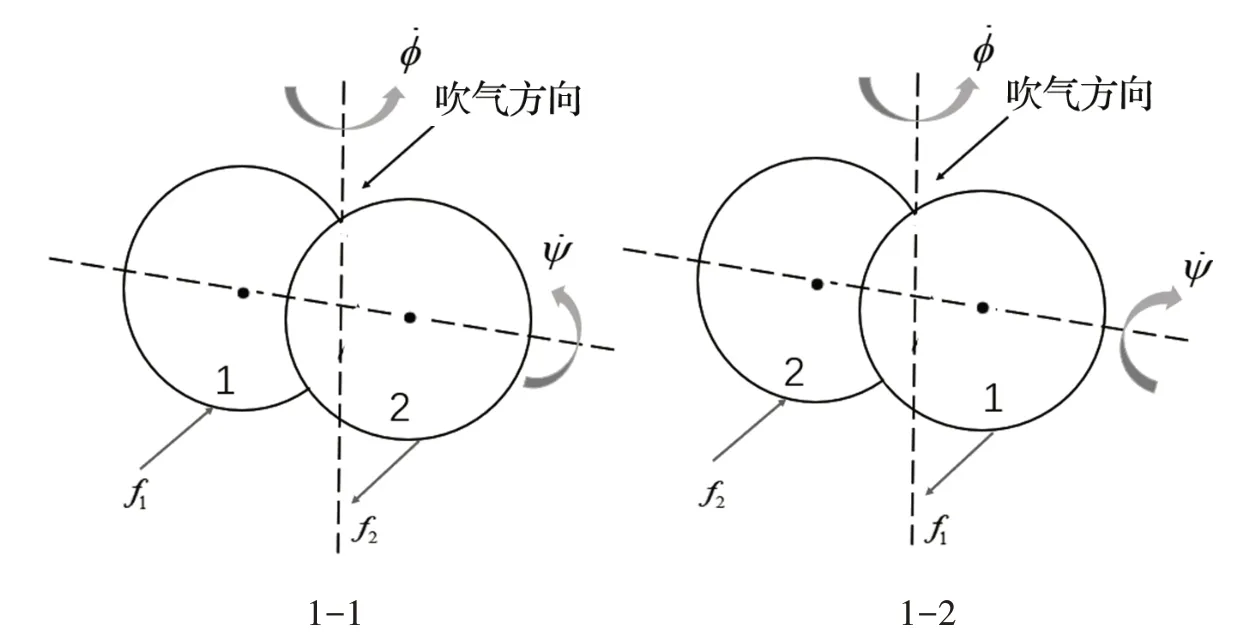
图1 飓风球在地面转动的情况

在每次实验中，吹气的管子相对飓风球的位置具有一定的任意性，所以的方向是随机的。不失一般性，图1给出其中任意一种情况，在此情况中，球1顺着公转方向滚动，而球2逆着公转方向滚动。

假设在图1-1中，吹气方向偏于球1，当飓风球公转180 度后，在图1-2中，吹气方向则偏于球2，但这两种情况下，吹气都促进飓风球公转；假设在图1-1中，吹气方向偏于飓风球的上部，吹气促进飓风球的自转，但当飓风球转过180度，在图1-2中，吹气阻碍飓风球的自转。所以在一般情况下，吹气产生的公转角速度比自转角速度大，以下都在此一般情况下讨论。

如图1 所示，球1 和球2 与地面的接触点绕公转轴和自转轴做圆周运动的半径与球1 和球2 的半径R相同。球1与地面的接触点绕公转轴和自转轴做圆周运动的分速度分别为，这两个分速度方向相反，球1 与地面的接触点相对地面运动的速度为，由于公转角速度比自转角速度大，球1 与地面的接触点向前滑动，摩擦力f1方向与其运动方向相反；球2与地面的接触点绕公转轴和自转轴做圆周运动的分速度也分别为，但这两个分速度方向相同，球2 与地面的接触点相对地面运动的速度为，球2与地面的接触点也向前滑动，摩擦力f2方向也与其运动方向相反。

球1 和球2 与地面的接触点相对于地面的加速度都有三个分量，其中两个分别是垂直指向公转轴和自转轴的法向角速度分量和，另一个是摩擦力产生的加速度分量，方向为沿球1 和球2 与地面的接触点所做圆周运动的切向方向。

从图1中不难看出，f1产生的力矩阻碍公转但促进自转，f2产生的力矩既阻碍公转又阻碍自转。

3 飓风球翘起原因的分析

以球1 与地面的接触点为参考点，尚未翘起的飓风球受到重力2mg和分别与两个法向加速度方向相反的惯性力，其中m是球1 和球2 的质量，如图2-1 所示。以下要讨论以球1 与地面接触点为支撑点球2 翘起的问题，所以在以上受力分析中没有考虑球2 受到地面的支持力，球1 受到地面的支持力和摩擦力也都没有考虑，因为它们过球1 与地面的接触点，不产生让飓风球翘起的力矩，与沿球1 与地面的接触点所做圆周运动切向方向的加速度相应的惯性力也没有考虑，因为它的方向与翘起的转轴平行，也不产生让飓风球翘起的力矩。

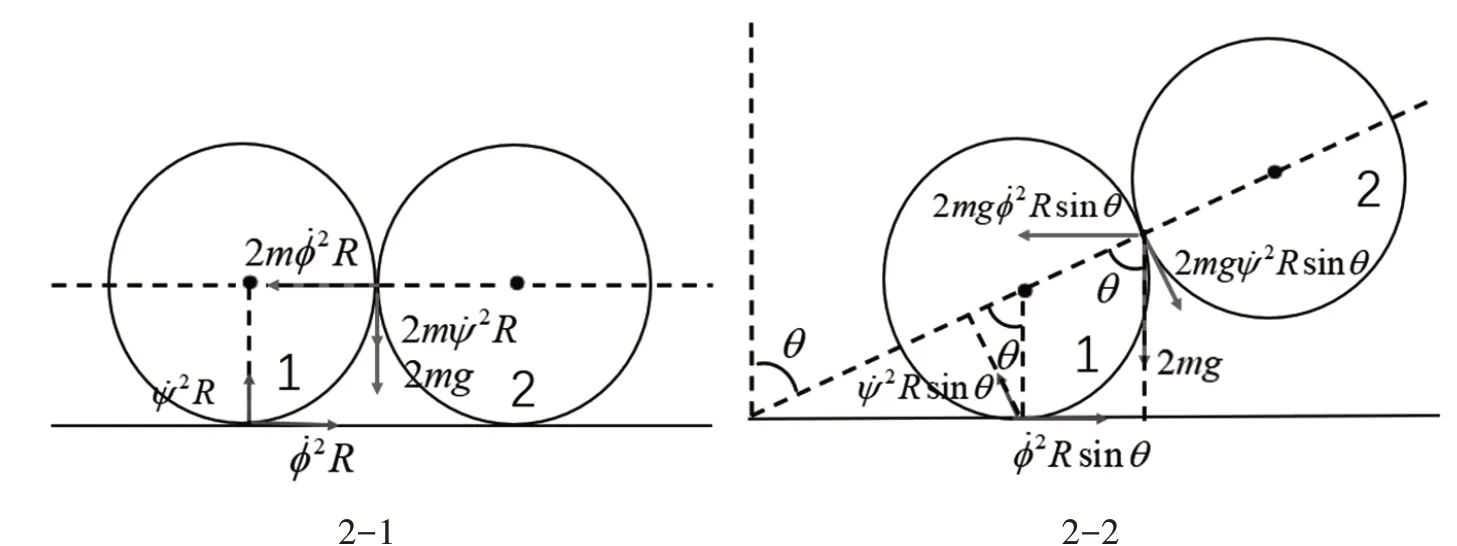
图2 以球1与地面的接触点为参考点，飓风球的受力分析

当球2翘起时，设过两球质心的自转轴与竖直方向的夹角为θ，称之为飓风球的站立角，球1与地面的接触点绕公转轴和自转轴做圆周运动的半径均为Rsinθ，如图2-2 所示，球1 与地面的接触点的法向加速度为以球1 与地面的接触点为参考点，飓风球受到的惯性力，它们产生的力矩大小分别为此时重力产生的力矩大小为2mgRsinθ，继续向上翘的条件是

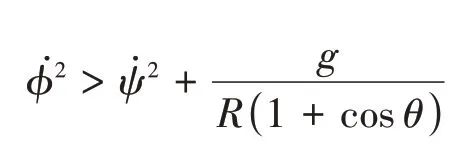
不难看出，如果以球2与地面的接触点为参考点，进行受力分析，讨论以球2与地面接触点为支撑点球1翘起的问题，结果与上面是一样的。但实际上，球2相对于球1更容易翘起，原因分析如下。

如图2-2 所示，当球2 翘起时，球1 与地面的接触点绕公转轴和自转轴做圆周运动的分速度分别为，这两个分速度方向相反，球1与地面的接触点相对地面运动的速度为，由于公转角速度比自转角速度大，球1与地面的接触点向前滑动，摩擦力f1方向与其运动方向相反，在摩擦力f1产生的力矩作用下，公转角速度减小，自转角速度?增大，球1 与地面的接触点相对地面的速度减小，当自转角速度和公转角速度相等时，球1与地面的接触点相对地面的速度为零，球1做无滑滚动，球1所受摩擦力f1=0，公转和自转加速度不变而达到稳定状态。

当球1翘起时，与以上的分析同理，球2与地面的接触点绕公转轴和自转轴做圆周运动的分速度分别为和，但这两个分速度方向相同，球2 与地面的接触点相对地面运动的速度不易减小到零，球2 与地面的接触点始终在地面上滑动而不能做无滑滚动，在摩擦力f2产生的力矩作用下，公转角速度和自转角速度持续减小，状态不稳定。

图3-1给出飓风球翘起过程的中间状态，以飓风球与地面的接触点为参考点，飓风球受到的惯性力之和2ma0，其中a0是法向加速度和之和，在翘起过程中从图3-1 中可以看出，惯性力之和2ma0对飓风球的翘起起到促进作用。

图3 以飓风球与地面的接触点为参考点，飓风球所受惯性力之和

图3-2 给出飓风球翘起达到的无滑滚动稳定状态，以瞬心为参考点，飓风球受到的惯性力之和，瞬心合加速度的方向指向飓风球的质心，飓风球所受合惯性力的方向则指向瞬心，此时只有重力产生力矩，其作用看似阻碍飓风球的翘起，但实际上重力产生的力矩让翘起的飓风球发生进动而保持稳定状态。这个问题在下一节讨论。

4 飓风球进动稳定状态的分析

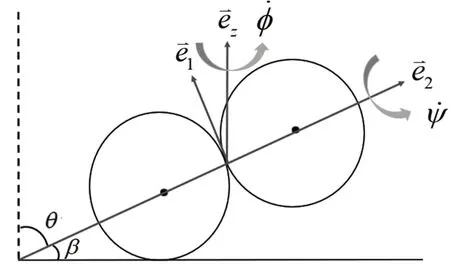
图4 飓风球三个惯量主轴方向上的单位矢量

则整个飓风球的角动量为

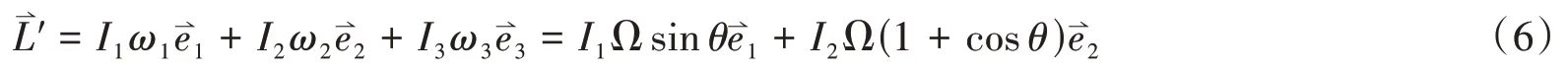
如前所述，当飓风球做无滑滚动时，以瞬心为参考点，只有重力能产生力矩，力矩为

图5 飓风球角动量的矢尖做匀速圆周运动

得出的翘起角和角速度之间关系与文献［1-2］得出的理论结果一致，而文献［2］的实验结果与理论结果符合较好。

5 结语

在一般教材［3-4］中，有质点的角动量定理、质点组的角动量定理，它们的参照系都是惯性系，其中质点组的角动量定理可推广应用于刚体，参照系是非惯性系的角动量定理也有，但仅限于质点组对质心的角动量定理和无滑滚动的刚体分析力学对瞬心的角动量定理两种特殊情况，而没有一般情况下非惯性系中的角动量定理，文章对此进行推导并用于分析飓风球的运动，而飓风球也是属于一般教材中少见的复杂问题。

文献［2］用分析力学推导飓风球的站立角度，把力学体系的运动方程以能量为基本概念的形式表达，使数学分析与几何和力学脱离开来，非常简洁精炼。文章用角动量定理分析飓风球的翘起过程，推导直观形象，并且辅以几何作图相对清楚透彻地分析其中的物理过程及其细节，两种方法优势互补。

教学内容的更新［5-8］是教学改革的重要方面，飓风球既可以作为学习拉格朗日方程和潘索自由旋转对称体理论一个具有指导性的练习，也可以作为引入非惯性系中角动量定理的实例。高校开展大学生物理学术竞赛活动，是大学生实践教学的一个重要举措，结合大学生物理学术竞赛进行各类教学活动，有利于提高学生综合运用知识去分析和解决实际问题的能力，使学生的知识、能力和素质得到全面的提升和发展。