基于神经网络和模糊补偿的水下机械臂控制

高 阳，张晓晖，高玉儿，尚 婷，杨启航

西安理工大学 自动化与信息工程学院，西安 710048

水下机械臂在海洋资源的开发和利用过程中扮演的角色越来越重要，它已成为水下机器人进行深海资源研究与勘探的重要工具，在海洋探索和资源开发中起到至关重要的作用[1]。与传统的工业机械臂相比，水下机械臂动力学模型具有时变、非线性、外部干扰和水动力干扰的特点，成为限制水下机械臂作业的主要因素。为进一步提升水下机械臂的运动性能，需要对水下机械臂的动力学模型以及运动控制方法进行更进一步的研究[2]。

国内外学者在水下机械臂的控制方面提出许多方法。谢宏等[3]提出了机械臂卷积神经网络滑模轨迹跟踪控制方法，通过此算法实现对机械臂轨迹跟踪的精确控制；魏娟等[4]提出了一种改进的径向基函数模糊神经网络算法来控制机械臂，使得控制系统的控制精度提高、收敛速度加快，有着良好的鲁棒性和控制性；Soltanpour等[5]提出了一种用于机器人手臂位置跟踪控制的模糊自适应滑模控制，降低了输入的计算量和抖动现象；刘建昌等[6]设计的高斯径向基函数神经网络补偿器可有效地补偿机械臂动力学模型的非线性，并具有较强的泛化能力和自适应能力；He等[7]采用径向基函数神经网络对机器人的动力学进行估计，成功地补偿了系统不确定性影响，提高了机器人系统的鲁棒性；杨亮等[8]采用RBF神经网络处理动力学参数不确定问题，将动力学分成两部分，分别设计两个神经网络同时处理，较好地克服电机参数漂移对跟踪控制性能的影响；徐智浩等[9]设计一种自适应模糊神经网络控制器，采用模糊神经网络补偿器，实现对系统中包括LuGre摩擦在内的非线性环节的逼近，并利用滑模控制项减小逼近并利用滑模控制项减小逼近误差。

RBF神经网络对非线性连续函数有着优良的动态逼近能力与自适应能力，能够以任意精度近似各种非线性函数和动态系统，且学习收敛速度快，需要的条件较少，网络结构简单，具有良好的泛化能力，能够大幅度提高设计和仿真的效率。因此，通过将RBF神经网络与传统滑模控制相结合，能够有效地改善滑模控制的“抖振”缺陷。但神经网络逼近分段连续函数的能力较差正是其进行摩擦补偿的难点所在，对于摩擦这类难以精确获取模型的参数，模糊补偿方法简单，不要求被控系统的精确数学模型，有着良好的动态性能。

基于以上研究，本文针对水下机械臂动力学建模复杂且控制算法精度不高的现有问题，建立了水下机械臂的精准动力学模型，并结合RBF神经网络控制和模糊控制在滑模控制器优化设计过程中的有效性，提出一种复合控制策略，该策略使用RBF神经网络逼近建模参数的不确定项，利用模糊控制补偿摩擦力造成的建模影响。通过仿真实验验证，本文针对水下机械臂提出的控制算法有较好的综合控制性能，能够实现良好的控制效果。

1 建立水下机械臂动力学模型

Lagrange法是通过计算控制系统的动能和势能，基于Lagrange约束得到动力学方程。由Lagrange法可以得到一组形式简洁的动力学方程，适合于计算机高速求解。本文使用Lagrange法求解机械臂动力学方程[10]。理想机械臂的动力学模型为：

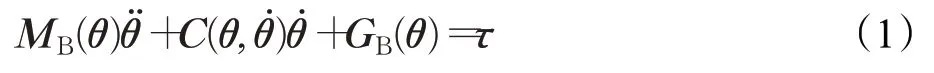
式中，MB(θ)是n×n阶正定惯性力矩阵，C(̇)是n×n阶离心力和哥氏力矩阵，其中GB(θ)是n×1阶重力矩阵，τ是关节力矩，θ、̇、̈依次是关节的角度、角速度、角加速度矩阵。二连杆串联机械臂模型示意图如图1所示。

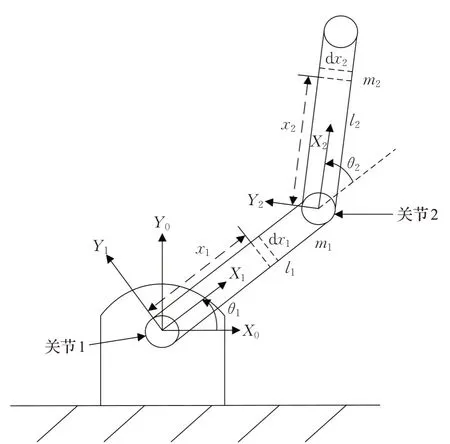
图1 二连杆串联机械臂示意图Fig.1 Schematic diagram of two-link series manipulator

基于Lagrange方法得到二连杆串联机械臂动力学参数为：

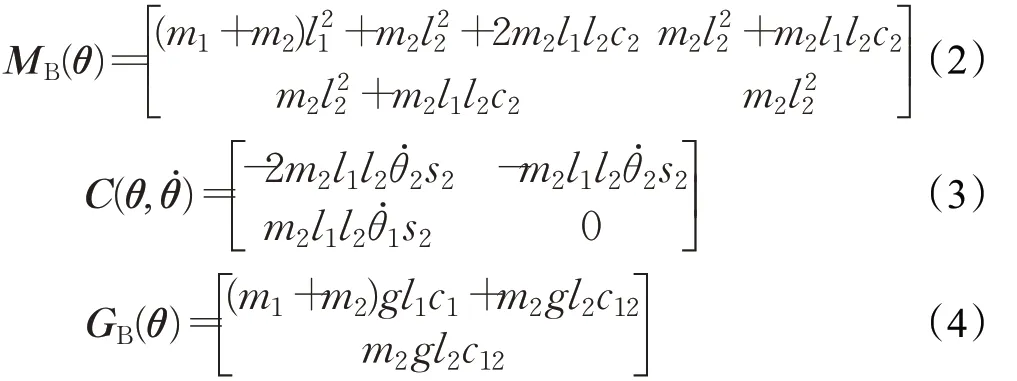
式中，c1=cosθ1，c2=cosθ2，s2=sinθ2，c12=cos(θ1+θ2)。

由于水下机械臂所处的工作环境复杂，控制系统的稳定性会受到水流、摩擦、外部干扰等因素的影响，因此水下机械臂的动力学分析需要考虑到部件与水流相对运动所受的力。

由流体力学可知，机械臂在水下的受力主要由水阻力Fd、附加质量力Fm、浮力Ff和升力Fl组成。

假设机械臂各连杆均是规则圆柱体，则升力为0。

1.1 水阻力矩和附加质量力矩计算

根据Morison方程[11]，水阻力和附加质量力为：

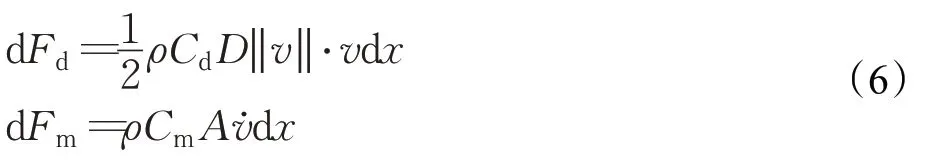
式中，dFd和dFm分别表示连杆单位厚度所受到的水阻力和附加质量力，ρ是流体的密度，D表示连杆的直径，A是水下机械臂连杆的横截面积，v是连杆速度函数，Cd是水阻力系数，Cm是附加质量力系数。由于实际的水阻力系数和附加质量力系数很难测量，一般使用常数。查阅相关文献后，本文取Cd=1.1,Cm=1[12]。

1.1.1 水阻力矩

当物体运动时，就会受到阻力的影响，水阻力就是由于机械臂与水的相对运动引起的。

关节1的角速度和关节2的角速度̇使连杆1产生法向速度，从而导致水阻力矩τD1的产生[13]，连杆1的水阻力矩为：

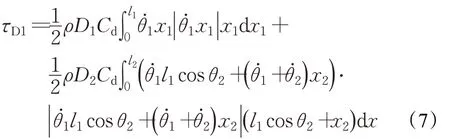
式中，x1是单位厚度dx1距离连杆1底端的长度，x2是单位厚度dx2距离连杆2底端的长度，l1是连杆1的长度，l2是连杆2的长度。

关节1的角速度̇和关节2的角速度也使得连杆2产生法向速度，进而导致水阻力矩τD2的产生[13]，同理可得，连杆2的水阻力矩为：

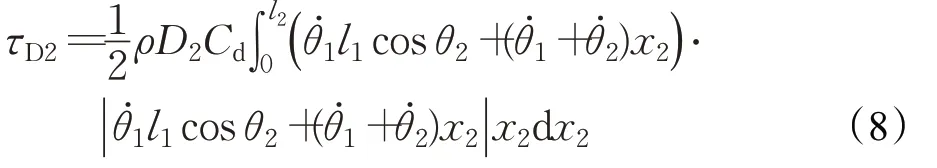
二连杆串联机械臂计算得到的水阻力矩为：τD=，水阻力矩阵DW为：

其中：

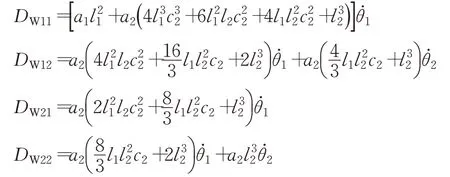
1.1.2 附加质量力矩

当物体在水中做加速运动时，物体周围的水也跟随其做加速运动，就会存在一个作用力使水做加速运动，同时物体必然受到一个反作用力，这个反作用力就称为附加质量力[13]。

连杆1所受的附加质量力矩τA1为：

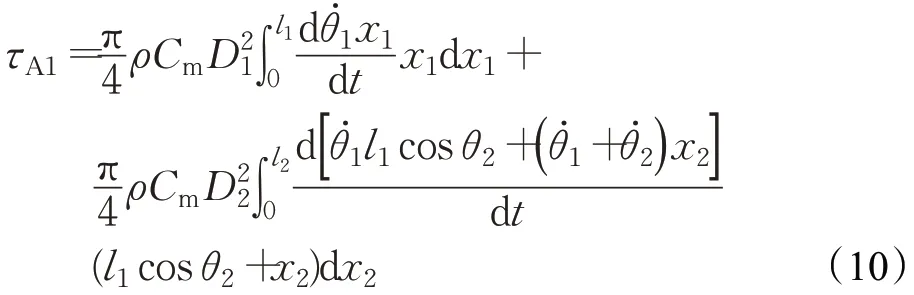
连杆2所受的附加质量力矩τA2为：

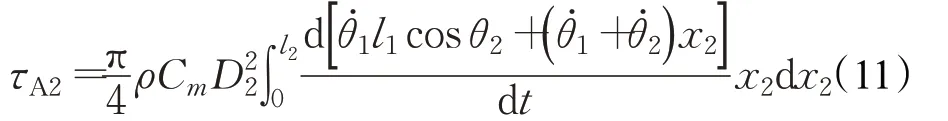
由式（10）和式（11）知，附加质量力矩表达式为：τA=，求得矩阵DA和MA为：

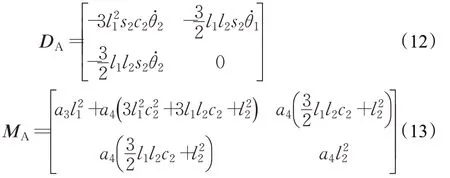
1.2 浮力力矩计算

由于重力和浮力方向相反，所以假设连杆重心和浮心重合的情况下，用等效重力代替重力和浮力[14]，则等效重力为：

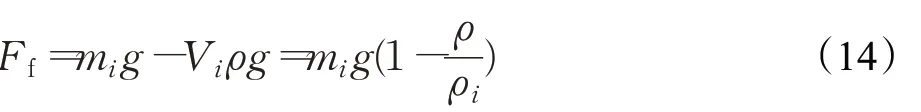
式中，mi是连杆i的重量；g是重力加速度；V i是连杆i的体积；ρ是水的密度；ρi是连杆i的密度。

所以两个连杆的等效重力G(θ)为：

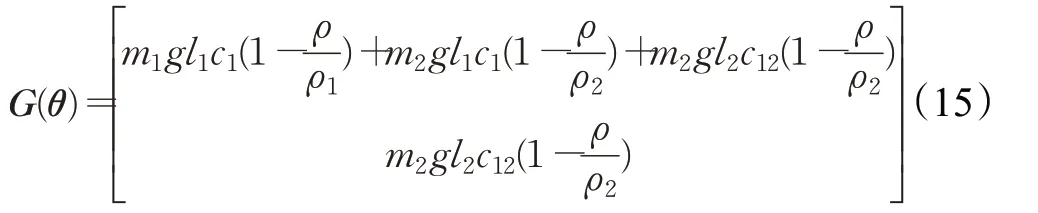
依据以上分析，建立基于Lagrange和Morison的水下机械臂动力学模型：

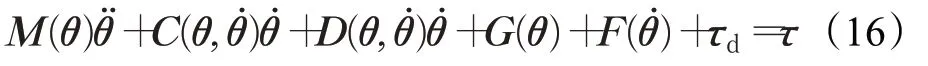
式中，M(θ)=MB(θ)+MA(θ)是含有部分附加质量力矩的正定惯性矩阵，表示离心力和哥氏力矩阵，是含有水阻力矩和部分附加质量力矩的矩阵，G(θ)∈Rn是等效重力矩阵，表示摩擦力矩阵，τd∈Rn是外部干扰，τ∈Rn是控制力矩。

2 水下机械臂控制系统设计

2.1 水下机械臂动力学模型分析

设机械臂实际角度为θ(t)，目标角度为θd(t)，则跟踪误差为：

定义滑模误差函数为：

其中Λ=ΛT＞0，联立式（17）与式（18），则：

结合式（16），可得：

式中：

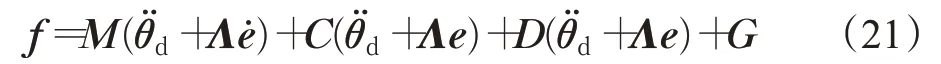
水下机械臂动力学模型中的参数主要分为以上两类，而大多数控制算法的改进针对这两种不同类型的参数使用同一种控制策略，由于水下机械臂控制系统的多耦合和非线性的特点，单独以神经网络或模糊控制作为控制策略存在局限性，对于这两种不同性质的参数使用不同的算法逼近是较为合理的选择。

对参数M、C、D、G使用整体RBF神经网络，不能精确地重构机械臂的水动力学方程[15]。而分块RBF神经网络可以对每个神经网络单独调整，从而简化了设计，实现更快的权重更新过程。

本文拟采用4个RBF网络分别逼近M(θ)、C(̇)、D(̇)和G(θ)。神经网络是一种具有高度非线性的连续时间动力系统，它有着很强的自学习功能和对非线性系统的强大映射能力[16]。对于伺服系统而言，摩擦环节是提高系统性能的障碍，使系统响应出现爬行、振荡或稳态误差[17]，本文基于模糊补偿摩擦力F(̇)的系统控制方法设计控制律。

2.2 控制律设计

（1）对f进行逼近

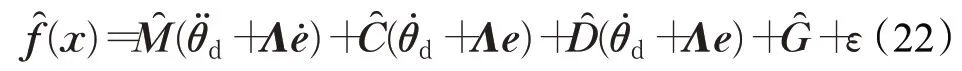
式中，ε为神经网络逼近误差。使用RBF神经网络，对(x)中的各项分别进行逼近：

自适应律取：

（2）对F的逼近

由于机械臂的摩擦力只与关节角速度相关，因此用于逼近摩擦力的模糊系统可表示为

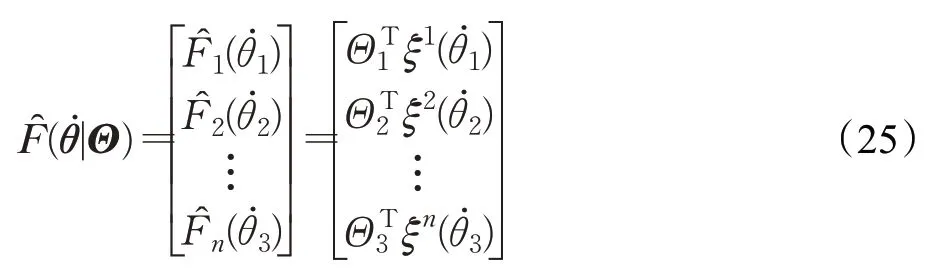
式中，ξ(̇)为模糊系统的基函数向量，Θ为自适应调节参数。

ξ(̇)为维向量，其第l1,l2,…,l n个元素为：

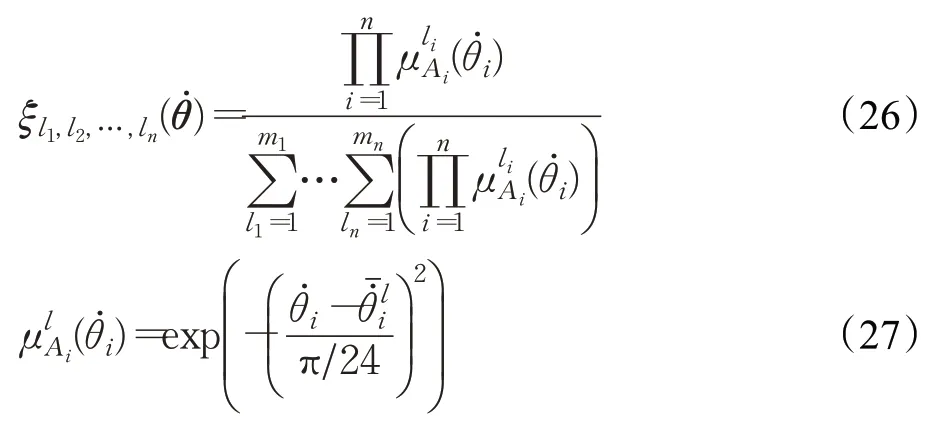
式中，分别为-π/6，-π/12，0，π/12和π/6，θ̇i的隶属函数如图2所示。

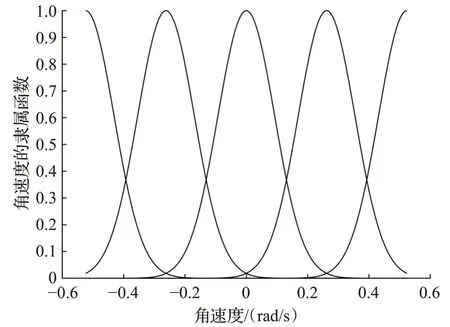
图2 的隶属函数Fig.2 Membership function oḟ

基于传统模糊补偿的控制器设计方法，设计模糊系统的自适应律为：

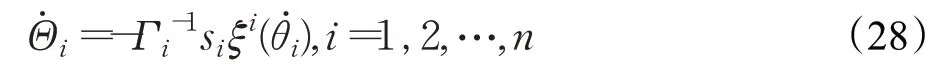
得到RBF网络和模糊系统的输出，设计控制律为：

式中，RBF神经网络对f的估计值为̑，模糊系统对摩擦力F的补偿输出为̑，K v是对称正定矩阵，v是克服RBF神经网络逼近误差ε的鲁棒项。

鲁棒项设计为：

2.3 稳定性分析

定义Lyapunov函数为：

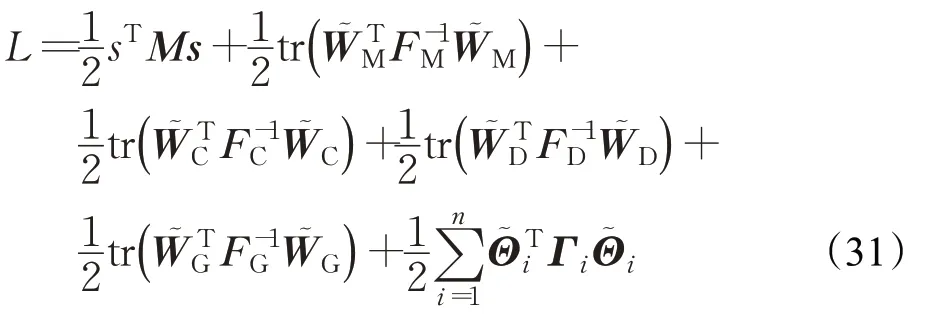
对Lyapunov函数求导可得：

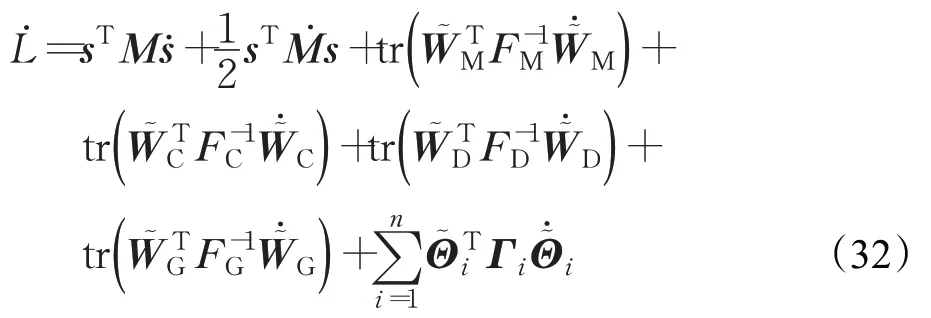
考虑到水下机械臂动力学的特性，将式（24）和式（28）代入式（32），得：

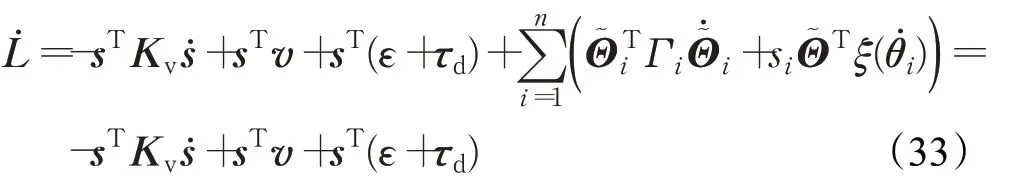
由于

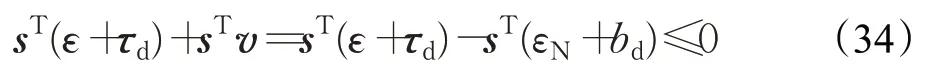
则̇≤0，根据李雅普诺夫稳定性定理，控制系统的稳定性可证。

根据设计合适的各种控制函数项和算法，本文设计的水下机械臂控制原理示意图如图3所示。

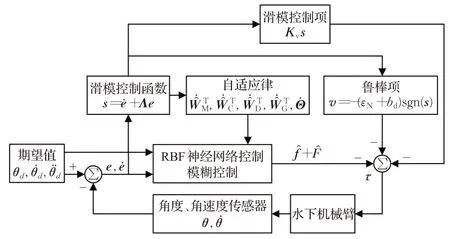
图3 水下机械臂控制原理Fig.3 Control principle of underwater manipulator

3 二连杆串联水下机械臂动力学仿真

3.1 仿真参数

仿真使用的二连杆串联水下机械臂的尺寸为：连杆1的质量m1=6 kg，长度l1=0.45 m，等效直径D1=0.1 m，密度ρ1=1 698 kg/m3；连杆2的质量m2=4 kg，长度l2=0.275 m，等效直径D2=0.1 m，密度ρ2=1 852 kg/m3[18]。

二连杆串联水下机械臂的关节角度的期望值为θ1d=θ2d=0.1 sint，关节角度和角速度的初值设置为：

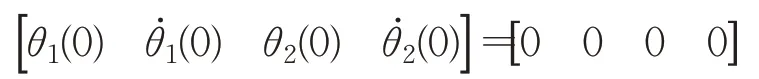
二连杆串联水下机械臂水动力学方程参数设置为：

（1）带有部分附加质量力矩的惯性矩阵为：

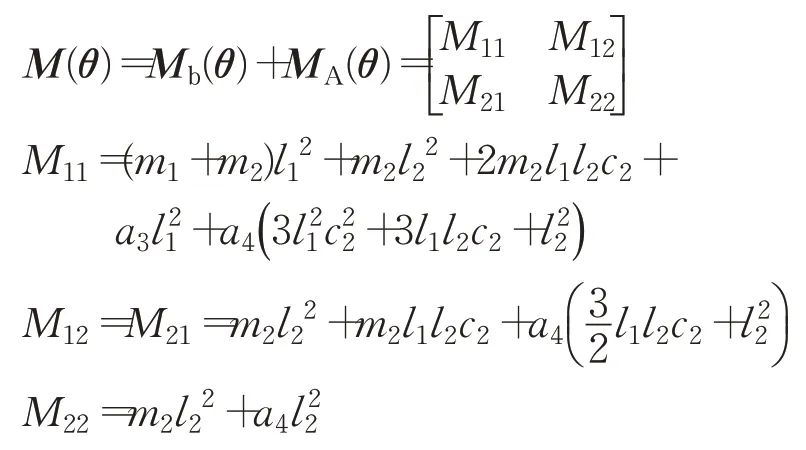
（2）离心力和哥氏力矩阵C(̇)由公式（3）求得。

（3）水 阻 力 矩 阵Dw(̇)和 部 分 附 加 质 量 力 矩DA(̇)的矩阵为：

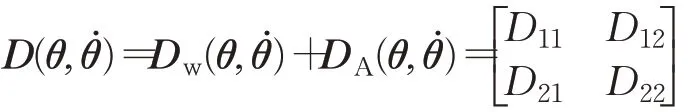
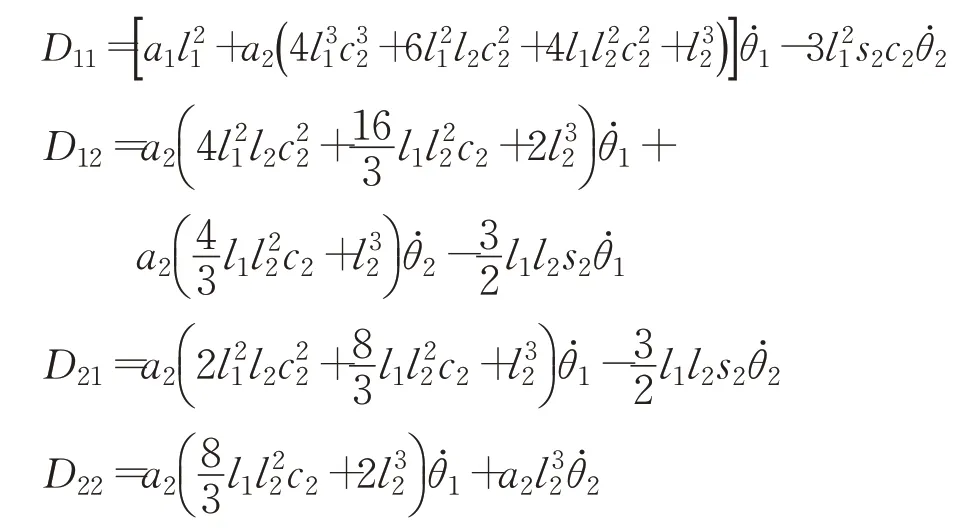
（4）等效重力矩阵G(θ)由公式（15）求得。

（5）摩擦模型为一般模型：库伦摩擦力+黏性摩擦力，则摩擦力矩阵F(̇)为：

其中，K1和K2分别表示库伦摩擦系数和黏性摩擦系数，取K1=0.2，K2=3。

（6）假设外加干扰项和水下机械臂期望运动轨迹一致，则外加干扰τd是0.1sint。

二连杆串联水下机械臂控制算法参数设置为：

本文四个RBF神经网络的高斯函数中，均值c i取[-1-0.5 0 0.5 1]，标准差b=10，权值矩阵中任意元素初值取0.1，滑模系数Λ=diag（10，10），K v=diag（30，30），鲁棒项中εn=0.1，bd=0.1，自适应律中FM、FC、FD、FG取对角阵，每个元素取值为100。

3.2 仿真结果与分析

本文使用了4种方法对二连杆串联水下机械臂控制系统进行仿真实验。其中，整体RBF神经网络、分块RBF神经网络和本文提出的控制算法的参数基本一致。关节1的输出力矩仿真如图4所示，关节2的输出力矩仿真如图5所示，两个关节的角度跟踪曲线如图6所示，误差曲线如图7所示。

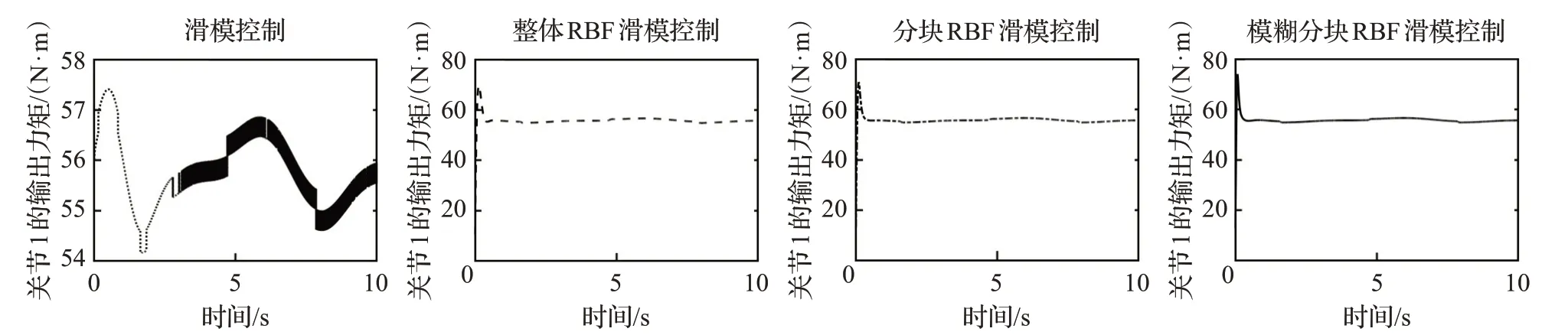
图4 不同算法下关节1的输出力矩Fig.4 Output torque of joint 1 under different algorithms

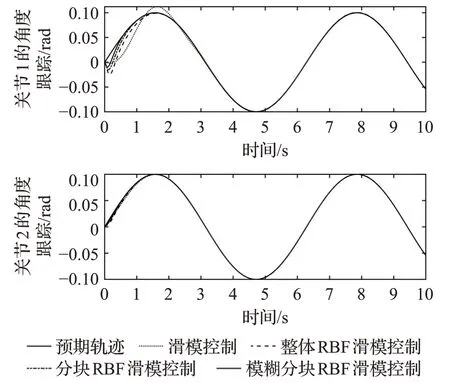
图6 两个关节的角度跟踪Fig.6 Angle tracking of two joints

由图4和图5可以得到，本文提出的算法有效地消除了滑模控制算法的天然缺陷——抖振，并且它的响应速度更快，能够更稳定、更快地输出合适的力矩。根据图7结果，对机械臂的关节角度跟踪误差从响应速度、均方差、平均误差和最大误差四个方面进行分析，结果如表1所示。

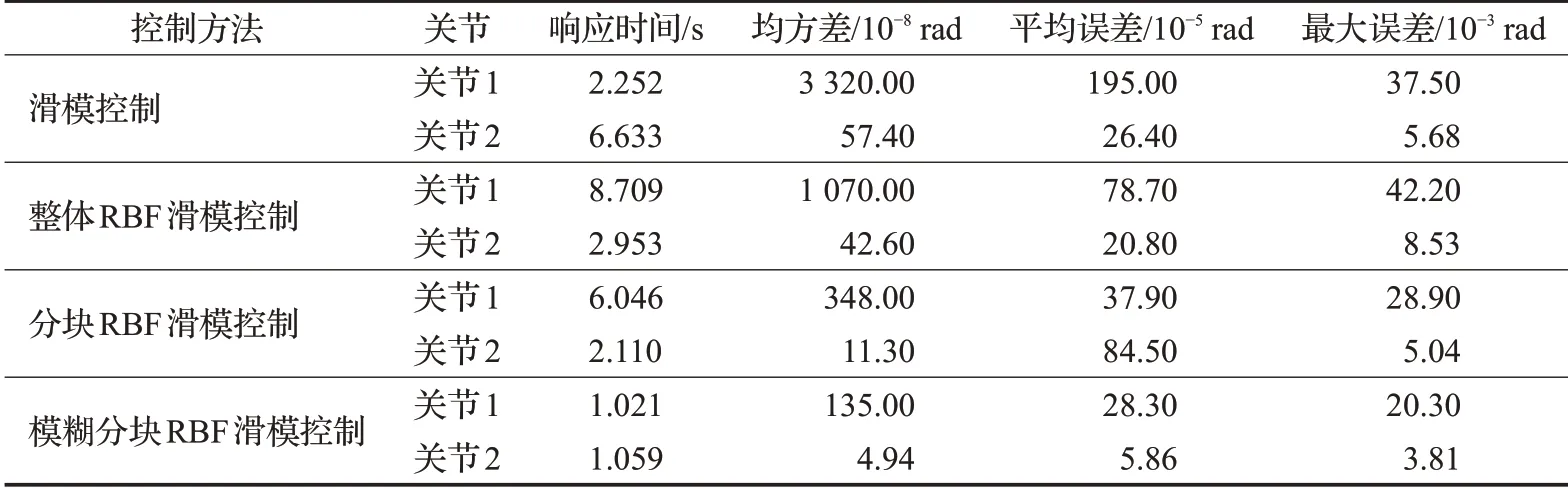
表1 二连杆水下机械臂各关节的角度跟踪误差分析Table 1 Angle tracking error analysis of each joint of two-link underwater manipulator

图5 不同算法下关节2的输出力矩Fig.5 Output torque of joint 2 under different algorithms

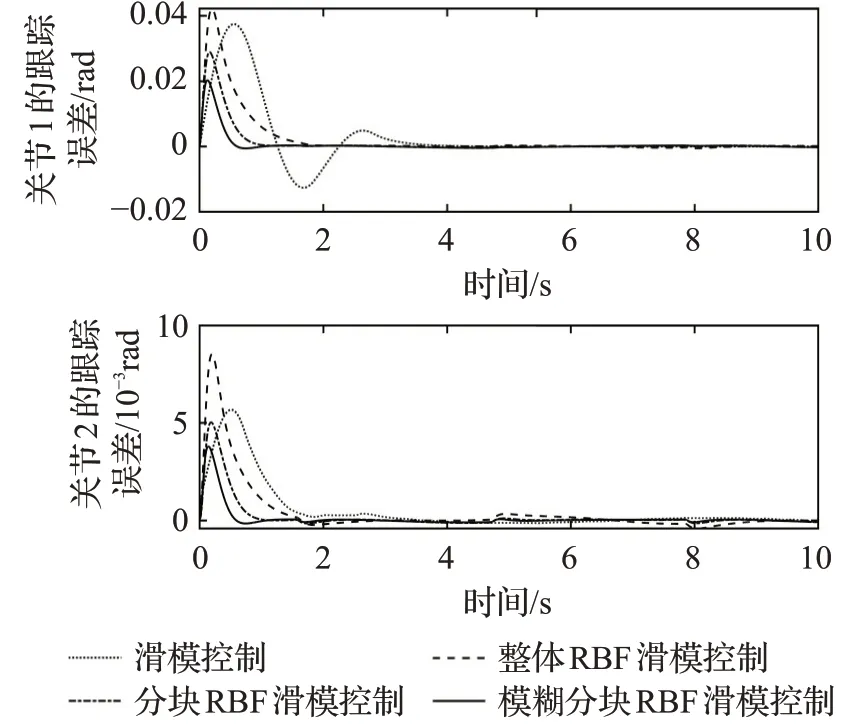
图7 两个关节的跟踪误差Fig.7 Tracking error of two joints

由表1可知，在二连杆串联水下机械臂控制系统的响应时间上，整体RBF滑模控制的响应时间较长，模糊分块RBF滑模控制的响应时间相比较其他控制算法大幅度降低，关节1的响应时间是1.021 s；关节2的响应时间是1.059 s，体现出了本文算法的响应速度有了显著提高。

在水下机械臂控制系统的轨迹跟踪误差上，传统的滑模控制的均方差、平均误差和最大误差都是这四种控制算法中最大的，存在需要改良的缺陷。相比而言，整体RBF滑模控制和分块RBF滑模控制误差会小很多，而本文的模糊分块RBF滑模算法的误差是四种控制算法中最小的，关节1的均方差是1.35×10-6rad，平均误差是2.83×10-4rad，最大误差是2.03×10-2rad；关节2的均方差是4.94×10-8rad，平均误差是5.86×10-5rad，最大误差是3.81×10-3rad。

本文算法与分块RBF滑模控制算法对比，关节1的平均误差降低了25.3%，关节2的平均误差降低了93.1%；与整体RBF滑模控制算法对比，关节1的平均误差降低了64.0%，关节2的平均误差降低了71.8%；与滑模控制算法对比，关节1的平均误差降低了85.5%，关节2的平均误差降低了77.8%。结果表明本文设计的模糊分块RBF滑模控制算法的控制效果要明显优于其他三种控制算法。

4 结论

本文针对水下机械臂控制系统提出了一种基于分块RBF神经网络和模糊补偿的自适应滑模控制算法。该方法使用分块RBF神经网络对动力学模型参数的不确定项M、C、D、G进行逼近，使用模糊系统对非参数的不确定项F进行补偿。并且结合自适应控制、鲁棒控制和滑模控制，改善了传统滑模控制抖振的问题。同时，该方法还降低了水下机械臂控制系统的跟踪误差，提高了水下机械臂控制系统的响应速度、稳态性能和抗扰性能，具有非常重要的实用价值。