纯策略纳什均衡的博弈强化学习
2022-08-09陈希亮赵芷若
王 军,曹 雷,陈希亮,陈 英,赵芷若
1.陆军工程大学 指挥控制工程学院,南京 210007
2.东部战区总医院 博士后科研工作站,南京 210002
DQN(deep Q-learning)算法[1-2]在Atari游戏中的完美表现标志着单智能体强化学习已取得重大突破,而多智能体强化学习由于维度爆炸、环境非平稳性和信度分配等问题依旧未能完全攻克。
近年来,将博弈理论融入到多智能体强化学习形成博弈强化学习取得了不错结果,典型算法有Nash Qlearning[3]和Mean field[4-5]。博弈理论和强化学习可以相互结合的原因主要有以下四点:(1)博弈论研究的主要是社会系统、经济系统的各类问题,并且这些系统的很多行为都依赖于计算机系统做出的决策和预测,如智能推荐系统和广告投放系统;(2)大多数经济系统和社会系统中的决策者都是多个个体或多个组织,与强化学习中多智能体形成对应关系;(3)大多数多智能体强化学习任务主要是希望在有限时间、有限资源、有限沟通下实现高效率计算并获得更高累积回报,而博弈论所研究的经济系统主要是在多个类型不同,限制不同的玩家中寻找出互惠且稳态的策略,因此两者都是在一定限制条件下的优化问题;(4)博弈论中根据玩家之间的利益关系而划分成的竞争型、合作型和混合型模型可以平行推广,用来描述强化学习中智能体的相互关系,然而博弈强化学习仍然有许多亟待解决的关键问题。
1 博弈强化学习关键技术问题
博弈强化学习除了多智能体强化学习的维度爆炸、环境的非平稳性和信度分配等固有问题外[6-7],还存在以下几个特有问题。
(1)如何平衡理性假设与探索利用。大多数博弈理论的结果都是基于理性人假设和共同知识假设,即博弈玩家所采取的策略都是为最大化自身的效用值,并且同步地认为对手也会采取最大化效用值的策略。然而强化学习主要是通过智能体与环境的不断交互,凭借试错机制和奖赏函数最大化自己的长期累积回报的期望,而试错机制的重要环节就是增加探索几率。如果智能体是完全理性的,则何时探索、何时利用是两个理论融合必须要考虑的问题。
(2)如何高效通用求解大规模博弈强化学习任务。大规模博弈问题的求解是博弈理论中的公开难点,主要由于大规模博弈问题不易建模,且多数为非凸问题不易求得近似解,因此利用强化学习中集中式训练分布式执行框架、值函数分解等是求解上述问题的一个新型思路,典型算法有MADDPG[8]、COMA[9]、VDN[10]和QMIX[11]等。但是这些算法还远未达到高效和通用的层次,基本都是在累加性和单调性等假设条件下对特定问题进行抽象、分解和转换,因此高效通用求解博弈强化学习任务仍需要重点关注。
(3)纯策略纳什均衡的存在性。诺贝尔经济得主Aumann曾说:“混合策略在直觉上是有问题的”。美国著名经济学家Roy Rander也指出“博弈理论没有广泛应用于各个领域的一个重要原因就是在于策略的随机性”。关于混合策略,博弈论大师Ariel Rubinstein给出了两种解释,一是解释认为混合策略是玩家认知能力的偏差和不完全信息共同作用的结果,另一种认为混合策略是基于所有玩家关于纯策略选择的分布,然而这种分布无法解释单个玩家的策略选择。同时,对于智能体而言混合策略纳什均衡的执行往往需要多次决策,并以频率替代概率,这种做法会花费更多的时间和精力。因此,混合策略一直以来都饱受诟病[12-13],更高效、敏捷的博弈强化学习更需要纯策略纳什均衡,然而在很多具有实际背景的博弈问题中,纯策略纳什均衡并非总是存在。
针对博弈强化学习中的纯策略纳什均衡问题的主要解决办法有如下几类:
(1)简化式方法。该类方法的主要思想是简化问题模型,仍然用混合策略的纳什均衡代替纯策略纳什均衡,该类方法的优势是使得问题可以求解,但是混合策略也会使得算法的计算量增加,并且最终学习到的策略在执行时也存在一些难度。该类的典型算法有Nash Q-learning和Friend or foe[14]算法。
(2)逼近式方法。由于纯策略纳什均衡并不总是存在,所以此类方法主要是利用其他解来逼近纯策略纳什均衡,例如ε-均衡[15]就是通过控制与纯策略纳什均衡的距离来保证问题的合理性,Lipschitz博弈[16]也是通过Lipschitz常数来控制智能体收益变化的幅度来求解具体问题。
(3)推理式方法。此类方法主要是基于当前的局部信息对对手进行建模,然后通过推理和预测得出对手的策略,然后在针对性的做出最佳反应。如此反复地进行上述过程直至最终收敛至稳定策略。此类典型的算法有OpenAI和牛津大学提出的LOLA算法[17]。
如何解决不存在纯策略纳什均衡的博弈问题正是本文重点讨论和解决的问题,针对此问题主要提出了元强化学习算法和基于分形维数的均衡程度评估模型,全文的逻辑框架如图1所示。

图1 逻辑框架Fig.1 Logical framework
2 主要概念
重点叙述文中涉及到博弈强化学习相关概念,如元博弈和元均衡。同时也会介绍基于分形的均衡程度评估模型中提及的分形及分形维数。关于马尔科夫决策过程和纳什均衡等基本概念不再过多描述,具体定义、符号和基本结论可在相关文献中查找[18-24]。
2.1 元博弈
对于n人一般式博弈,其关于智能体i的一阶元博弈iG可以表示成:
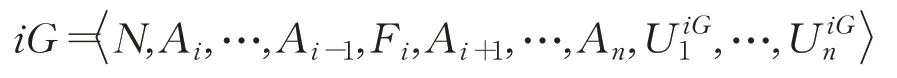
其中,Fi表示智能体i的反应函数空间。反应函数的定义为f:A-i→A i。对于智能体i的任意反应函数f∈F i,以及其他智能体的任意联合动作a-i∈A-i,有
2.2 元均衡(Meta equilibrium)
对于一个n人一般式博弈G及该博弈中某个联合动作a,如果存在一个元博弈θG和这个元博弈的一个纯策略纳什均衡σ*,满足φ(σ*)=a,则称联合动作a为博弈G的一个元均衡[25],也可以称a为元博弈θG导出的一个元均衡。
2.3 盒维数(Box dimension)
假设P∈Rn为非空有界集,Nε(P)为能够覆盖集合P所需要的最小网格数,且此这些网格中最大直径为ε,定义集合P的上盒维数和下盒维数分别为:

如果集合P的上下盒维数相等,则称该值为集合P的盒维数[26]。
2.4 Weyl分数阶微积分
假设f(x)∈C(I),0<v<1,如果f(x)逐段可积,则f(x)的v阶Weyl分数阶积分[27]定义如下:

记BV I为在I上所有有界变差函数的集合,C(I)为所有在I上连续的函数集合。
3 均衡建模模型
解决不存在纯策略纳什均衡博弈问题的首要是对均衡问题进行合理建模,然后利用现有理论和算法进行科学求解。目前主要建模及求解方式有如下二种,一是转换为具体表格形式,再利用压缩映射求解不动点问题。二是转换为具体线性或非线性函数[28-29],利用李雅普诺夫稳定性理论求解。
3.1 基于不动点理论的均衡模型
不动点,即方程f(x)=x的解,博弈问题中的均衡解是使博弈过程达到一种稳态的策略。在问题规模比较小且状态为离散时,可将玩家的策略、状态以及效用分别以表格形式进行存储,通过Banach不动点定理进行求解,Banach不动点定理的主要内容如下:
引理1(Banach不动点定理)[30]如果f是完备距离空间(X,d)到自身的压缩映射,则在X中一定能找到唯一的x∈X,使得f(x)=x,即x是压缩映射f在X上唯一的不动点。
下面结合具体的博弈问题,给出利用Banach不动点定理求解不动点的详细过程,求解过程基于以下两条假设:一是玩家的动作空间和状态空间都是完备的距离空间,二是构造出的策略选择函数f是压缩映射。因此在运用该框架求解时应对上述两点假设进行合理证明和解释。
假设博弈玩家的数量为n,并且具有相同动作集A=(a1,a2,…,an),初始阶段时任取x0=(y1,y2,…,yn),其中y i∈A,设策略选择函数f的Lipschitz常数为β,d(x n,x n-1)=d(f(x n-1),f(x n))≤βn-1d(f(x0),x0),同时,对于任意给定的n和k,根据完备空间中关于距离的三角不等式,可知:
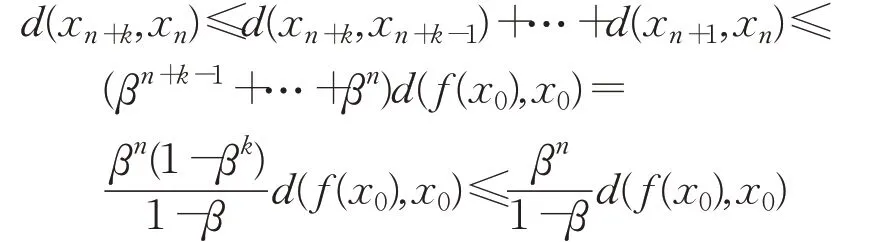
因此,{x n}为Cauchy列,结合空间的完备性可知:
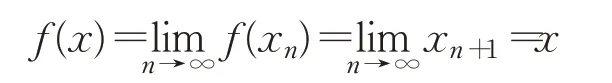
如果x*是另外一个不动点,则:

所以x=x*,即唯一性得证。
3.2 基于李雅普诺夫稳定性的均衡模型
该建模方法的核心思想主要是将玩家已选取策略、当前状态和环境一起看成一个系统,通过寻找并建立合适的Lyapunov函数L(x),再利用李雅普诺夫稳定性理论来判定当前状态是否稳定,稳定性定义如下:
(1)对于任意状态x,∀t0,∀ε>0,∃δ(t0,ε)使得‖x(t0)‖<δ(t0,ε),则称该状态为李雅普诺夫稳定的。
(2)对于任意状态x,∃δ(t0)>0,‖x(t0)‖<δ(t0)使得,则称该状态为渐进稳定的。
上述两类稳定性的主要区别在于渐进稳定的状态在出现扰动后会随着时间的推移逐渐回到状态x,而李雅普诺夫稳定意味在出现扰动后平衡点仍在一定范围内移动,两者的具体解释可见图2。

图2 稳定性解释Fig.2 Explanation of stability
点A与点B的区别在于,分别给两点一个任意扰动后,点A将脱离原状态并无法回到原始状态,但是点B仍然能够回到原始状态,因此点A是在李雅普诺夫稳定性理论下是不稳定的,点B是稳定的。点C在施加扰动后如果仍在圆中波动,则称其为李雅普诺夫稳定的。点D在受到扰动后,如果最终会收敛到原点则称其为渐进稳定的。在针对具体问题抽象建模时,可依据实际将其建模成线性系统或非线性系统,并且二者的判定依据有所差异。
(1)线性系统:x=A x,矩阵A的所有特征值为λ=a+bi。如果a≤0,b=0,则为李雅普诺夫稳定的;如果a<0,b=0,则为渐进稳定的,否则为不稳定的。
(2)非线性系统:针对x=x0,如果L(x0)=0,并且L(x)≥0,L′(x)≤0,x为除x0以外所有点,则称x0为李雅普诺夫稳定的;如果L(x0)=0,并且L(x)>0,L′(x)<0,x为除x0以外所有点,则称x0为渐进稳定的,否则为不稳定的。
运用过程中,最主要的难点在于如何找到合适的Lyapunov函数L(x)。
4 元均衡博弈强化学习算法
Howard在1971年提出的元博弈理论,其核心思想是在原有博弈基础上构建一种假想博弈,称为元博弈,元博弈导出的元均衡是一种纯策略纳什均衡,元均衡和纯策略纳什均衡最主要区别在于,不存在纯策略纳什均衡的博弈也存在元均衡,在任意一个一般式博弈中,至少存在一个元均衡,从该博弈的完全元博弈中导出的元均衡一定存在。同时,元均衡能够保证每个玩家的效用值高于某个阈值,因此元均衡所对应的策略具有一定的合理性。
4.1 元均衡的合理性和存在性
引理1联合动作a为元均衡的充要条件为:

定理1在任一般式博弈G中,元均衡一定存在。
证明设G为n人一般式博弈,对于扩展博弈1G和智能体1,可以找到最优反应函数,对于∀a-1∈A-1有:

因此,f1(A-1)在博弈1G中是对其他智能体的联合动作的最佳反应。以1G为基础博弈再以智能体2进行扩展,形成博弈21G。在21G博弈中,在智能体1始终采取f1(A-1)情况下,可以找到智能体2的最佳反应函数为:

从上述推导过程可知,f2(A-2)是对其他智能体的任意联合动作的最佳反应。重复上述构造过程可知,由G推导出的元博弈n…1G的元均衡一定存在。
4.2 元均衡博弈强化学习算法复杂度
Meta EquilibriumQ-learning算法的主要改进在于智能体动作集的替换,元博弈是以原始博弈为基础,元博弈中智能体的动作变成对于其他智能体的联合动作的反应函数。联合动作的数量由于组合变化的多种可能使得联合动作的数量大幅增加,因此元博弈中的动作空间与原始博弈动作空间相比会增大。
以二人矩阵博弈为例,||S=m为状态集的大小,为玩家动作集的大小,因此双人矩阵博弈的空间复杂度为2m42。扩展成元博弈1G后,玩家1的反应函数集大小为:

所以元博弈1G的空间复杂度为2m4×312。基于元博弈的算法模型虽然增加了空间复杂度,但是该算法在理论上可以保证纯策略纳什均衡的存在性。
Meta EquilibriumQ-learning算法的伪代码如下:
1.初始化
2.令t=0,获得初始状态s0
3.对于智能体i,获取对应的元博弈iG,反应函数f∈F
4.对于所有的s∈S,f i∈Fi,令
5.选取动作f it
7.更新,对于j=1,2,…,n

MetaQt j(s′)为元博弈中的纯策略纳什均衡中的Q值,αt∈[0,1]
8.令t=t+1
4.3 收敛性证明
Meta Equilibrium Q-learning算法的收敛性证明基于Schauder不动点定理,具体内容如下:
引理2(Schauder不动点定理)A是赋范线性空间中的凸紧集(如果A⊂X,∀x,y∈A,t∈[0,1],tx+(1-t)y∈A,则A是X中的凸紧集),对于从A到A的连续映射f,存在不动点使得f(x*)=x*。f t是完备空间Q到Q的映射:

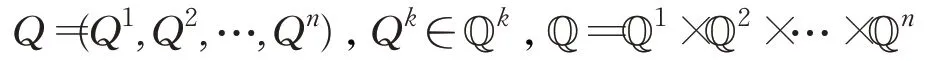
其中:

定理2Q是Q函数空间,对于任意的Q1,Q2∈Q,定义如下范数:

则该范数满足非负性、齐次性和三角不等式。
证明(1)非负性:对于每个

当且仅当智能体保持静止不采取任何动作。
(2)齐次性:∀x∈R,Q∈Q

(3)三角不等式:任意Q1,Q2∈Q

因此,上述定义的范数有合理性。对于s,a1,a2,…,an,令

所以,f(Q*)=E◦P(Q*)=Q*。
定理3Q是一个凸集,并且f是Q到Q的连续映射。
证明由于Q=Q1×Q2×…×Qn,


记元均衡为σ*,则

此处r k(s,σ*)是从状态s到s͂的累积回报,由于Q kx和Q ky是收敛的,则tQ kx+(1-t)Q ky也是收敛的,即tQ kx+(1-t)Q ky∈Qk,Q是一个凸集。

同时:
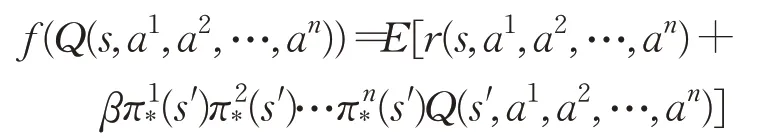
通过函数连续性定义可知,
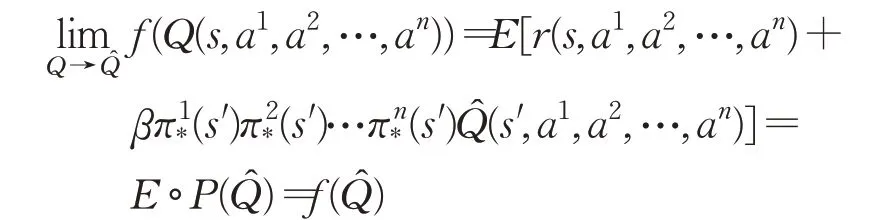
f是Q到Q的连续映射。因此,根据上述论述过程可知,映射f满足Schauder不动点定理条件,并且Q是一个凸集,即映射f的不动点σ*存在。如果智能体的每个动作和状态都能随机的采样,并且学习率满足:

则算法最终会收敛至Q*。
4.4 实例验证
(1)福利博弈:福利博弈模型中的玩家分别为政府和贫民,政府愿意救济努力寻找工作的贫民,但是不愿意救济在家待业的贫民。然而,贫民只有在政府不救济的情况下才会努力寻找工作,福利博弈的支付矩阵如表1所示。

表1 福利博弈的支付矩阵Table 1 Payout matrix of welfare game
通过验证可知(救济,寻找工作)、(救济,在家待业)、(不救济,寻找工作)和(不救济,在家待业)都不是纳什均衡。因此,福利博弈中不存在纯策略的纳什均衡。记政府为玩家1,贫民为玩家2,一阶元博弈1G中贫民的反应函数的集合为(f1,f2,f3,f4):
f1:无论政府救济还是不救济,贫民始终工作;
f2:无论政府救济还是不救济,贫民始终待业;
f3:如果政府救济就工作,不救济则待业;
f4:无论政府救济就待业,不救济则工作。
则一阶元博弈1G的支付矩阵如表2所示。

表2 一阶元博弈1G的支付矩阵Table 2 Payout matrix of first-order metagame 1 G
通过计算可知,一阶元博弈1G存在纯策略纳什均衡σ*=(救济,f4),则

即(救济,在家待业)是原始福利博弈的一个元均衡。原始博弈中四个策略的总效用值如下:
(救济,寻找工作):总效用值为5;
(救济,在家待业):总效用值为2;
(不救济,寻找工作):总效用值为0;
(不救济,在家待业):总效用值为0;
从总体效用可知该策略并不是最优策略,但是在保证得到纯策略的前提下,该策略是最合理策略。
由于福利博弈中并不存在纯策略的纳什均衡,而Nash Q-learning算法要求博弈的每个阶段都存在鞍点或全局最优点,因此Nash Q-learning算法在福利博弈中难以收敛,然而利用元均衡替代纳什均衡形成的Meta Equilibrium Q-learning算法仍然可以此问题。
(2)夺控战:夺控战中,红蓝双方的起始位置分别为2号地域和1号地域,双方在对抗的每个阶段每次只能移动至与其相连的地域,如蓝方首次可到达的地域编号分别为3、4和6,红方首次可到达的地域编号分别为4、5和7。双方对抗的核心目标都是尽快占领14区域。
具体对抗中,如果双方同时到达除14号以外的区域,系统将对双方做出处罚,并将双方分别移动至上个阶段的各自位置,如在对抗的第一阶段,红蓝双方都移动至4号区域,则系统将会使红蓝双方分别重新回到2号和1号区域。如果其中一方优先达到14地域,则该方获胜,对抗结束。对抗示意图如图3所示。

图3 夺控战Fig.3 Control war
具体实验中,奖赏函数的设置为到达目标区域获得回报值为100;如果双方到达同一位置,则分别获得回报值为-1;其他情况下的回报值为0。以Nash Q-learning算法作为参考。两种算法的具体实验结果如图4所示。

图4 两种算法实验结果图Fig.4 Experimental results of two algorithms
实验结果表明,Meta Equilibrium Q-learning算法收敛时间比较长,但是两个算法的累积回报相差不大,这表明在保证纯策略的纳什均衡的前提下,使用Meta Equilibrium Q-learning算法解决类似博弈问题更有优势。然而,Meta Equilibrium Q-learning算法也有很大的改进空间,算法使得智能体的动作集变成对于其他智能体联合动作的反应函数集,这使得动作空间较原始博弈会大幅增大,从而使得算法的时间复杂度会增加。对于元博弈中智能体的反应函数,从福利博弈的具体实例可以看出某些特殊的反应函数不满足合理性和科学性,所以反应函数可以进一步优化。同时,均衡解的求解被证明是NP-hard问题,因此寻求更高效的求解方式也是博弈强化学习研究的重难点,基于群体智能优化算法是否能够为求解均衡解带来新的突破也寄希望于后续研究。
5 基于分形维数的均衡程度评估模型
元均衡博弈强化学习算法的缺点主要是由于动作集的扩大而导致计算量递增,为提高算法计算效率,如果能够评估某些特定状态与均衡状态的距离,则可以人为地引导智能体向正确的方向收敛,以减少算法计算时间。李雅普诺夫稳定性理论虽然可以评估系统的稳定性,但是在实际运用过程中发现,很多博弈问题通过此方法建模后,很难找到合适的Lyapunov函数,导致没法判定状态是否趋于稳定。但是均衡状态与非均衡状态在本质上是有所区分的,因此应该有其他可以刻画此差异的指标。
分形维数最早是用于度量某些不规则的集合和函数,如三分康托集、谢尔宾斯基垫片和Koch雪花曲线等。分形维数较拓扑维数的优点在于其度量的尺度更加精确,能够扑捉特殊集合和系统的内部构造,同时分形维数的计算与构造Lyapunov函数相比更加简单。分形维数的种类有很多,常见的分形维数有Box维数、豪斯道夫维数和K-维数,每种维数的计算方式也有差别,应用最广泛的是Box维数和豪斯道夫维数,本文主要计算的是Box维数,因为它是豪斯道夫维数的天然上界,且更易于编程和计算。关于一般连续函数的分形维数主要有以下定理。
5.1 分形维数定理
定理4任意给定的有界变差函数f(x):
(1)f(x)的Box维数为1;
(2)f(x)经过Weyl分数阶积分后的函数的Box维数依然是1;
(3)任意连续函数的Box维数大于等于1小于等于2。
证明假设是分划点并且满足:
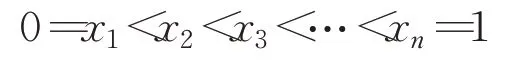
则:

假设m为等于或者大于ε-1的最小整数,令Nδ是f(x)图像与ε-网正方形相交的正方形的个数,则:

令1≤i≤m-1,同时令:
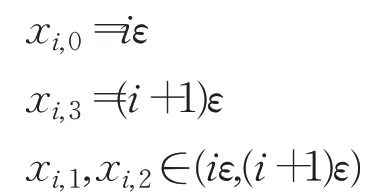
则:
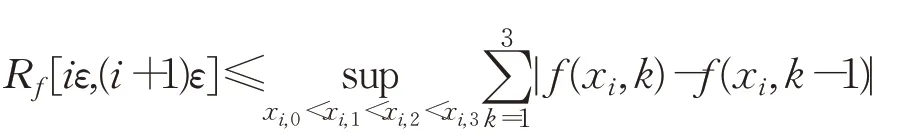
所以存在一个确定的常数C使得Nδ≤Cε-1。
结合Box维数的定义可知:
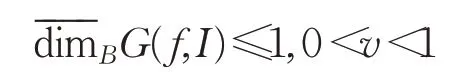
又因为连续函数f()x的拓扑维数不小于1,所以
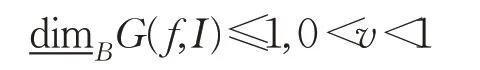
由于f(x)∈C(I),并且f(x)在I上是有界变差函数,由实变函数可知,f(x)可以被写成两个连续且单调递增函数w1(x),w2(x)的差,即:

这里w1(x)=h1(x)-c,w2(x)=h2(x)-c,同时在区间[1,+∞)上,h1(x)=h2(x)=c,显然可知h1(x)、h2(x)也是单调递增的连续函数。
(1)如果f(0)≥0,选定w1(0)≥0和w2(0)=0,根据Weyl分数阶积分的定义可知:

由连续的定义知当w1(x)在I上连续时,G1(x)仍然在I上连续。令0≤x1≤x2≤1和0<v<1,则:

因此函数G1(x)在I上仍然是一个单调递增的连续函数。同理可得G2(x)是一个单调递增的连续函数。
(2)如果f(0)<0,选定w1(0)=0和w2(0)>0,使用类似的讨论即可得出D-v w1(x)和D-v w2(x)在I仍然是单调递增的连续函数。所以,D-v f(x)在I仍然是一个有界变差函数。由于任意给定的一元连续函数无法超出整个平面,因此其Box维数小于等于2。
5.2 分形评估模型计算流程
基于分形维数的均衡程度评估模型中计算的分形维数是盒维数,该方法将智能体的动作、状态、回报和环境等看成多维空间的点,对于任意状态s,将初始状态s0到s的多个点构建为空间中不规则点集,通过求解该点集的盒维数来判断此状态与均衡状态在空间中的距离。盒维数越大状态越稳定,离均衡状态距离越近。但在具有求解过程发现,随着网格最大直径的变化,盒维数也在不断变化,因此模型最后采用最小二乘法对盒维数进行拟合处理。分形评估模型计算流程如下:
1.数据归一化
2.计算权重因子:

3.计算N(P):为点到原点的距离
4.计算盒维数:B=lnN(P)lnr
5.最小二乘法拟合盒维数

在上述夺控战的红蓝博弈中,从开始至对抗结束,分别依次选取四个状态,记为s1,s2,s3,s4,计算其盒维数并进行最小二乘法拟合后的结果如图5所示。
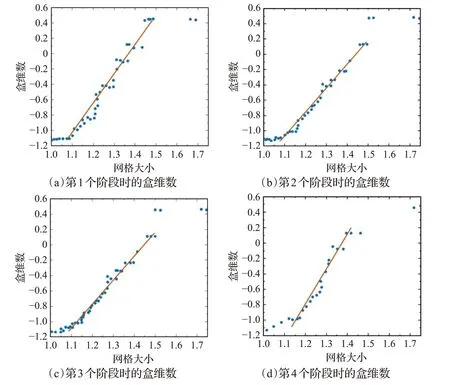
图5 四个状态的盒维数拟合结果Fig 5 Box dimension fitting results of four states
从拟合结果可知,第四个状态s4的盒维数最大,因此该状态相对最稳定,离均衡状态的距离最近,这与具体的博弈进程一致。
6 结论
纯策略纳什均衡运用于强化学习算法中的效率相比于混合策略纳什均衡要高很多,但是纯策略纳什均衡的存在性在实际问题中并不能总是得到有效保证,Meta Equilibrium Q-learning算法主要的优势如下:
(1)能够保证纯策略纳什均衡的存在性
该算法通过反应函数将原始博弈转换为元博弈,而从元博弈推导出来的元均衡必定是纯策略纳什均衡。因此能够有效解决纯策略纳什均衡的存在性问题。
(2)能够保证最终策略的科学性
Meta Equilibrium Q-learning算法中智能体的动作空间会增加,但是所有智能体的回报会大于某个特定的阈值,这使得智能体有意愿选择该策略,因此该算法学习到的最终策略具有科学性。
(3)能够扩大算法应用的范围
解决纯策略纳什均衡意味着Meta Equilibrium Q-learning算法能够解决一些不存在纯策略纳什均衡的问题,因此该算法的应用范围要大于一般强化学习算法。
博弈强化学习目前还处于发展阶段,即概念融合阶段。例如,Nash Q-learning主要利用纳什均衡引导智能体快速收敛,FFQ(Friend-or-Foe)则是通过划分智能体为朋友和敌人以达到削减博弈规模的目的,并且上述算法和结论都依赖于博弈论中理性人假设和共同知识假设。因此,博弈强化学习在后续的研究中需要考虑的问题仍然有很多,一是如何解决“战争迷雾”下的博弈强化学习。博弈充满了不确定性,博弈也可划分为完美信息博弈和不完美信息博弈、完全信息博弈和不完全信息博弈,则此时的问题是建模成扩展式博弈模型还是部分可观测下的马尔科夫决策模型,两种模型内部又存在何种联系。二是如何解决非对称下的博弈强化学习。目前博弈强化学习所解决的问题局限在德扑和网格世界等游戏环境中,重要的是此时各智能体的动作集都是相同的,即对称博弈。然而,博弈强化学习的落地无法回避非对称博弈强化学习,虽然基于复因子动力学等方法通过将非对称博弈转换为对称博弈进行求解,但此类方法远未达到通用效果,且高度依赖于专业领域知识对模型进行抽象和简化。博弈强化学习的现有成果指明了学科交叉融合是解决该问题的正确思路,未来持续不断地研究和新领域知识的加入必将解决博弈强化学习的现有难题,使其广泛应用于各个领域。
