多标签特征选择研究进展
2022-08-09周慧颖汪廷华张代俐
周慧颖,汪廷华,张代俐
赣南师范大学 数学与计算机科学学院,江西 赣州 341000
传统的监督分类解决了一个实例只有一个标签的问题,将其视为单标签分类,包括二分类和多类情况。然而,在许多实际情况中,一个实例可能同时与多个标签关联[1]。例如,一幅画可以属于政治,也可以属于宗教或者是地方冲突[2]。这种学习任务称为多标签分类[3-4]。
在过去,多标签分类的主要动机是文本分类[5]。文本一般含有一个以上的概念类,例如一篇晚间新闻可以同时归类为娱乐或者体育。如今,多标签分类在生物信息学[6]、图像标注[7]、视频分类[8]、音乐分类[9]和语义场景分类[10]等方面得到了广泛的运用,例如在图像标注中,一个视频片段可能与一些场景相关,如城市和建筑等。类似地,在音乐分类中,一首交响乐可能同时属于多个类别。
在大数据时代,由于数据维度高、量级大和冗余特征多等特点,机器学习算法面临的任务越来越复杂,为知识挖掘与发现带来了诸多挑战,降低了数据价值密度,影响分类模型效率,易产生维数灾难[11]。特征选择是实现数据降维的有效手段之一。特征选择基于某一评价标准,从原始数据集合中选择出最优的特征子集,使得分类器的性能得以保持甚至提高。在实际应用中,越多的特征可能导致数据收集成本越高,模型解释难度越大,预测器的计算成本越高,有时泛化能力也会降低[12]。因此,在实际学习之前进行特征选择是很重要的。
与单标签学习一样,多标签数据通常具有数千甚至数万个特征,图像和文本尤其如此。例如,一个网页或文件的集合选择了数百万信息词汇来反映它们的主题。对于给定的学习任务,许多特征是冗余的、不相关的,这可能会给学习任务带来很多缺陷,如计算量大、过拟合、性能差。为了解决这一问题,研究者们提出了多标签特征选择算法,以降低多标签数据的维数,提高分类学习的准确性,生成更紧凑、更泛化的分类模型。因此,多标签特征选择是模式识别、机器学习、数据挖掘等领域的重要研究课题,也是现在研究热点之一。
1 知识基础
1.1 特征选择
特征选择的目的是确定可用特征的子集,这是最有区别性和最具信息量的数据分析。在实际应用中,更多的特征可能与更高的数据收集成本、更困难的模型解释、更高的预测器计算成本有关,有时还会降低泛化能力[12]。因此,在实际学习之前进行特征选择非常重要。传统上,特征选择技术从不同角度有两种分类方法[13]。一是根据分类问题中类别标签等监督信息的可用性,可分为有监督、无监督和半监督三种方法。当有足够的标签信息可用时,监督特征选择起作用,而无监督特征选择算法不需要任何类标签。半监督特征选择是监督和无监督方法之间的一种折衷,这种方法可以在标记数据有限的情况下同时利用有标记数据和无标记数据。二是根据选择策略的不同,分为过滤式方法、包裹式方法和嵌入式方法。过滤式方法选择特征子集作为预处理步骤,独立于选择的学习机器。包裹式方法利用所选预测器的学习性能来评估所选特征的质量。嵌入式方法利用学习算法的内在结构,将特征选择嵌入到模型学习中[14]。
通常,特征选择过程包括四个基本步骤[15],即子集生成、子集评估、停止准则和结果验证。在第一步中,根据给定的搜索策略选择候选特征子集,在第二步中根据一定的评价准则评价候选特征子集。在满足停止准则后,从所有已评价的候选对象中选择最适合评价准则的子集。在最后一步中,选择的子集将使用领域知识或验证集进行验证。其中,子集生成实质上是一个启发式搜索的过程,搜索空间中的每个状态指定一个候选子集进行求值。它包含了3个不同的策略,即完全搜索、顺序搜索和随机搜索。子集的优劣总是由一定的准则决定的(即用一个准则选择的最优子集不一定是根据另一个准则选择的最优子集)。评价标准可以根据其对挖掘算法的依赖程度大致分为两类,即独立标准和依赖标准,最终这些算法将应用于选定的特征子集。生成程序和评价函数会影响停止标准的选择。基于生成过程的停止准则包括:是否选择了预定义的特征数量,以及是否达到预定义的迭代数量。基于评价函数的停止标准可以是,添加(或删除)任何特征是否不会产生更好的子集;是否根据某个评价函数得到最优子集。循环继续,直到满足某个停止条件。通过向验证过程输出选定的特征子集,特征选择过程停止。结果验证的一种直接方法是使用数据的先验知识直接度量结果。它试图通过执行不同的测试来测试选定子集的有效性,并将结果与先前建立的结果进行比较,或者与使用人工数据集、真实数据集或两者的竞争特征选择方法的结果进行比较。具体流程如图1所示。
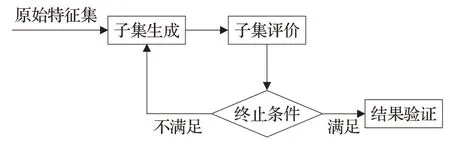
图1 特征选择框架Fig.1 Feature selection framework
1.2 多标签分类
现有的多标签分类方法大致可以分为两大类[16]:(1)问题转换法(problem transformation methods),即将多标签分类问题转化为一个或多个单标签分类问题的方法。(2)算法适应法(algorithm adaptation methods),即通过采用扩展特定学习算法直接处理多标签数据来解决多标签学习问题。多标签学习的任务是从多标签训练集D中学习一个函数h:X→2L。对于任何未知的实例E i(x i是一个d维特征向量,Y i是与x i相关的标签集合),多标签分类器h(·)预测h(x i)⊆L为x i的适当标签集。为了便于参考,表1列出了本文中使用的主要符号及其数学含义。

表1 主要符号及其数学意义Table 1 Main symbols and their mathematical significance
1.2.1 问题转换法
基于问题转换策略的多标签分类方法是将多标签数据通过特定的过程分解为一个或多个单标签数据,并使用单标签分类器进行分类。接下来,执行与此相反的过程,将分类后的单标签数据转换为多标签数据。
(1)二元关联法(binary relevance,BR)。它是多标签分类最常见的问题转换方法。该方法将多标签学习任务转化为q个独立的单标签二元分类问题,其中一个为L中的标签。换句话说,原始数据集被分解为q个数据集,其中包含所有实例原始数据集,如果原始实例的标签包含y(正实例),则标记为y,否则标记为-y(负实例)。最后,为了对一个未知的多标签实例进行分类,BR通过查询每个单独的二元分类器上的正标签然后组合这些标签来预测其关联的标签集Y。与其他多标签方法相比,BR方法的优点是计算复杂度低。对于一定数量的例子,BR与标签集L的大小q成线性比例,因此,对于一般情况下q不是很大的情况,BR方法是非常合适的。然而,在不同的领域中可以找到大量的标签,一些分治方法已经被提出,将标签组织成树形层次结构,这样就可以处理比q小得多的标签集。
标准BR算法的主要缺陷有:(1)完全忽略了标签间可能存在的相关性以及存在的冗余属性;(2)可能会导致类别不平衡问题。为了克服该缺陷,研究者们提出了这种方法的不同变体,如文献[17]提出了一种新的多标签分类链接方法CC(classifier chain)和文献[18]在分类器链的基础上提出了一种基于树型的标记依赖关系的分类器链算法TCC(tree-based classifier chain)。针对分类器链算法预测性能不足以及链序问题,文献[19]提出了一种基于梯度提升的多标签特征选择算法。
(2)标签幂集法(label powerset,LP)。这种方法将多标签学习问题转化为单标签多类分类问题。其主要思想是把每个样本所属的标签集Y i看作一个单标签yY i,训练集数据中出现的所有具有不同值的yY i组成一个单标签集合LY,为了对未知的多标签实例进行分类,LP首先查询多类分类器的预测,然后将其映射回L的幂集,从而预测其关联的标签集Y。与BR不同,LP考虑了标签之间的相关性,但随着标签的增加,新类的数量急剧增加,容易导致训练阶段的复杂度增加。在这些情况下,类的数量可能会变得非常大,同时许多类与很少的训练示例相关联。LP的另一个缺点是它只能预测以前出现在训练集中的标签集,不能推广到外部的标签集[20]。文献[21]提出的多标签分类方法即RAkEL(random k-labelsets)和文献[22]提出的用于多标签分类的广义标签集集成方法GLE(generalizedk-labelsets ensemble)克服传统LP方法的缺点,减少类的数量,提高分类的性能。文献[23]提出了一种基于剪枝的问题转化法PPT(pruned problem transformation),这是对LP算法的一种改进,但这种不可逆的转换可能会导致类信息的丢失。
1.2.2 算法适应法
这类算法通过采用流行的学习技术直接处理多标签数据来解决多标签学习问题,其核心是算法对数据的拟合。它包括Boosting算法、KNN(Knearest neighbor)算法、决策树算法、神经网络算法、支持向量机(support vector machine,SVM)算法等。其中,Boosting算法较为代表性的算法是BoosTexter[24](a Boosting-based system for text categorization),它是对Boosting改进算法AdaBoost.MH和AdaBoost.MR进行的扩展。KNN是一种分类算法,对于每个测试样本,首先在训练数据中检测出K个最近邻,然后将测试样本分配给其近邻中最常见的一个类,其代表性算法为ML-KNN[25](a lazy learning approach to multi-label learning),它是基于不可见实例的相邻实例的标签集的统计信息,利用最大后验准则来确定不可见实例的标签集。张敏灵[26]针对其未充分考虑样本多个标签之间的相关性,提出了改进算法IMLLA(an improved multi-label lazy learning approach)。决策树算法代表性算法为ML-DT[27](multilabel decision tree),它是在C4.5基础上提出的一种允许叶节点使用多个标签的算法。神经网络算法中较为代表性的有BP-MLL[8](back-propagation for multi-label learning)和MMP[28](multi-class multi-label perceptron)。BP-MLL是由流行的反向传播算法推导出来的,它通过使用一个新颖的误差函数来捕捉多标签学习的特征;MMP是一组基于感知器的多标签数据标签排序的在线算法,它为每个标签保留一个感知器,但每个感知器都必须执行权重更新才能得到较好的标签排序结果。SVM算法中较为代表性的有Rank-SVM[29],它通过最小化Ranking Loss,将SVM扩展到多标签数据学习中;Xu[30]针对Rank-SVM缺乏检测相关标签的自然零点,提出了一种通过增加一个零标签来定义一种新形式的排序损失和简化Rank-SVM的原始形式的改进方法,它大大降低了计算成本。
1.2.3 评价准则
对于多标签分类,有多个评价指标,本文主要介绍几个经典的评价指标[3]。这些度量通过分别评估学习系统在每个测试示例上的性能,然后返回整个测试集的平均值来工作。
(1)子集精度(subset accuracy)

其中,〚·〛如果·成立则返回1,否则返回0。子集精度评估正确分类的例子的比例,即预测的标签集与原本真实的标签集相同。直观上,子集精度可以被视为传统精度度量的多标签对应指标,并且往往过于严格,特别是当标签空间(即q)较大时。
(2)汉明损失(Hamming loss)
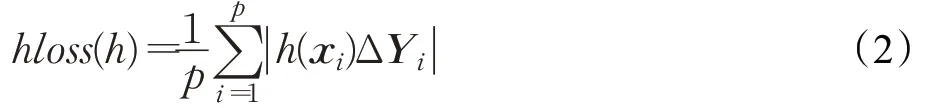
这里,Δ表示两个集合的对称差,|·|返回集合·的基数。汉明损失计算的是错分类标签的百分比,即与错误标签相关联的样本或属于不被预测的真实样本的标签。
(3)精度(accuracy),查准率(precision),查全率(recall),加强调和平均(Fβ)

此外,Fβ(h)检测是Precision(h)和Recall(h)的综合版本,具有β>0平衡因子,最常见的选择是β=1,这会导致查准率和查全率的调和平均值。
(4)1-错误率(one-error rate)
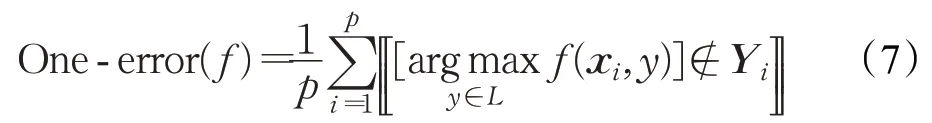
1-错误率计算排名靠前的标签不在相关标签集中的例子的比例。
(5)覆盖率(coverage rate)
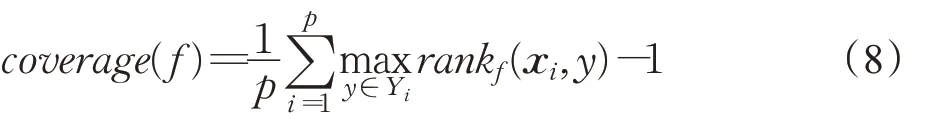
其中,rank f(x,y)根据f(x,·)的降序返回y在L中的排序。覆盖率计算平均需要沿着标签列表向下走多远才能覆盖示例的所有相关标签。
(6)排名损失(ranking loss)
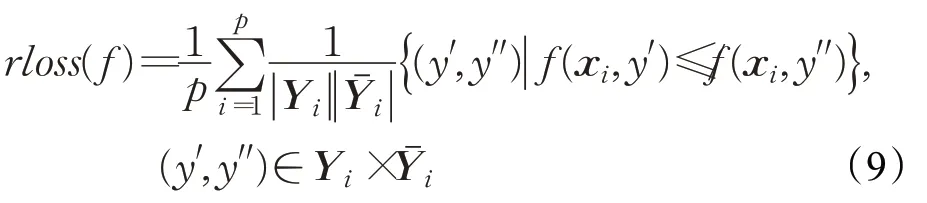
其中,是Y的互补集。排名损失计算的是逆序标签对的比例,即不相关标签的排名高于相关标签。
(7)平均精度(average precision)
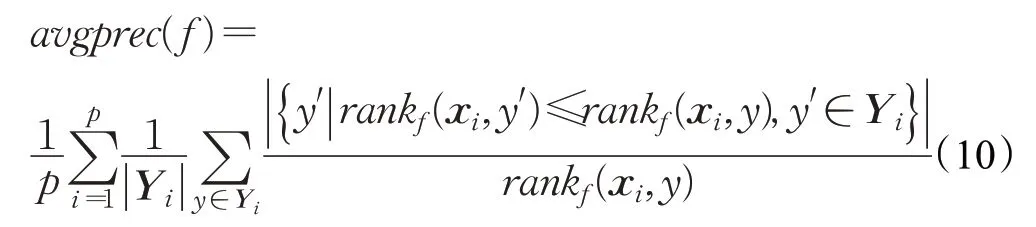
平均精度评价的是排在某一特定标签y∈Y i之上的相关标签的平均分数。
对于上述度量(除平均精度和精度外),度量值越小,系统性能越好,覆盖率最优值为,1-错误率和排名损失最优值则为0。对于平均精度和精度的多标签度量,度量值越大,系统性能越好,最优值为1。
2 多标签特征选择
不同于单标签特征选择,多标签特征选择所面临的问题更多,比如数据样本具有高维的特征,冗余、不相关的特征更多,此外每个特征与多个标签相关联,标签之间也存在一定的关联性。而标签的关联性也使得多标签特征选择面临着更多的可能和挑战。根据特征选择与分类器的关系,多标签特征选择可以分为基于过滤式的多标签特征选择,基于包裹式的多标签特征选择,基于嵌入式的多标签特征选择三种,如图2所示。

图2 多标签特征选择的分类Fig.2 Classification of multi-label feature selection
2.1 基于过滤式的多标签特征选择
特征选择过程独立于具体的学习算法,通过数据本身选择最相关的特征,即基于数据的内在属性来评估特征,而不使用任何可以指导相关特征搜索的学习算法,特征选择的过程与后序学习器无关。依照是否对多标签数据集进行分解,可以进一步分为基于问题转换的多标签特征选择和基于算法适应的多标签特征选择。
2.1.1 基于问题转换的方法
主要思想:在使用问题转换策略的多标签特征选择方法中,分解步骤类似于基于问题转换的分类。这里,首先对单标签数据应用合适的单标签特征选择方法,确定要选择的显著特征。然后在原始多标签数据中选择这些特征,并删除其他特征。在这一步中,使用多标签分类器来评估所选特征子集的性能。
针对1.2.1小节提出的BR未考虑标签相关性[3]以及存在冗余属性[31]的问题,文献[32]提出基于标签相关性和特征选择的二元关联算法FLBR(binary relevance with feature selection and label correlation)。该算法使用信息增益为每个标签选择与其相关的特征属性,同时针对现有考察标签相关性方法存在的冗余依赖和错误传播问题,采用控制结构的方式考察标签相关性。文献[33]提出了一种基于标签空间相关性的改进分类器链算法LSCC(an improved multi-label classifier chain algorithm via label space correlation),用于处理大规模多标签学习的特征选择和标签链序列优化。同时,结合标签空间降维与改进多标签分类器链算法的优势,提出了一种基于LSCC的标签空间降维算法。针对分类器链标签排序是随机决定的和所有标签都是插入到链中的两个问题,文献[34]提出了一种带有特征选择的部分分类器链方法PCC-FS(partial classifier chain method with feature selection),该方法利用了标签和特征空间之间的相关性,但该方法只使用了logistic回归方法作为二分类器,未考虑其他二分类器。
基于1.2.1小节提出的LP方法中类别多、类别不平衡问题,文献[35]提出一种利用互信息的多标签特征选择算法,首先应用PPT方法对问题进行转化,然后以多维互信息作为搜索标准进行贪婪前向搜索策略,实验验证了该方法的有效性。文献[36]提出了可扩展的Relief-F多标签学习方法PPT-Relief-F,该方法首先使用PPT将多标签问题转换为单标签问题,然后利用Relief-F算法为特征分配权重。
目前的基于问题转换的多标签特征选择方法的局限性在于,它们需要一个预处理步骤,将多标签问题转换为单标签问题,这个过程可能会导致后续问题。例如,如果转换后的单标签由太多的类组成,学习算法的性能可能会下降。此外,如果在转换过程中发生信息丢失,特征选择就不能考虑标签关系。
2.1.2 基于算法适应的方法
在传统的单标签学习中,一个样本只与预定义标签中的一个相关联,而在多标签学习中,一个样本可能同时属于多个标签。高维样本向量包含了一些不相关和冗余的特征,增加了计算复杂度,甚至降低了分类性能。目前,这一问题是通过特征选择技术,从原始特征中选择一个高度相关和低冗余特征的子集。而现有多标签特征选择算法大多仅仅考虑了特征间及特征与标签的相关性,忽略了不同标签之间的相关性。
(1)未考虑标签间的相关性
过滤式特征选择算法一般使用距离度量标准、相关性度量标准、一致性度量标准或信息度量标准来衡量特征与标签之间的相关性,特征的冗余性,比如:ReliefF、互信息(mutual information,MI)、最大相关最小冗余(maximal relevance and minimal redundancy,MRMR)、Hilbert-Schmidt独立性准则(Hilbert-Schmidt independence criterion,HSIC)等。不同评价标准可能获得不同的最优特征子集。
①使用ReliefF准则衡量特征与标签相关性
通过对多标签数据的研究,在传统单标签特征选择算法ReliefF的基础上,文献[37]提出了一种用于多标签图像分类的特征选择的ReliefF(multi-label ReliefF,ML-Relief F)和F统计量(multi-label F-statistic,MFstatistic)方法的扩展。但该模型只考虑了成对标签之间的关联度。马晶莹等人[38]提出了基于ML-ReliefF的特征选择算法,并研究了最接近相似样本和异构样本的搜索方法。Xie等人[39]提出了一种针对不平衡数据集的ML-Relief特征选择算法来降低维度。然而,这些算法都有其不足之处。例如,冗余特征不能通过删除低权重的特征来消除;在确定最近邻样本时,使用ML-ReliefF随机选取的样本较少,导致特征权重波动较大[38]。为了解决这些问题,文献[40]在多标签邻域决策系统中提出了一种新的基于ML-ReliefF和邻域互信息的多标签特征选择方法,该方法采用已知的相似样本和非均匀样本之间的平均距离来评价样本之间的差异,但其需要耗费大量的时间且不能较好地平衡所选特征子集的大小和分类性能。文献[41]提出了基于全局样本相关性的改进ReliefF多标记特征选择算法,但仅依靠特征与标签之间的相关性选择特征子集,忽略了标签间的依赖关系,并且该算法只适合处理小规模数据集。Slavkov等人[42]将RReliefF算法用于回归,提出了用于分层多标签分类任务的HMC-ReliefF(ReliefF for hierarchical multilabel classification)算法,但没有考虑不同类型的层次结构。
基于ReliefF的多标签特征选择方法一般步骤是首先提出一种判断样本是否同类与异类的模型,并将其引入改进的ReliefF算法中用于判断随机样本的近邻同类和异类,然后用于多标签数据集中给样本赋权重,迭代更新权重,最后根据特征权重选择特征子集。此类算法能够有效地提高分类的性能,但样本数量过少易导致权重的波动。其中,最优方法可以解决不稳定性以及预测精度低的问题,还可以解决采用ReliefF搜索最近样本时可用随机样本少的问题,并且降低了计算复杂度,去除了冗余特征,提高了分类性能。
②使用MI衡量特征与标签相关性
MI作为变量的依赖度量,可用于评估变量的关联度,并测量一个变量与另一个给定变量之间减少的不确定性[43],例如两组随机变量A、B之间的MI定义如下:
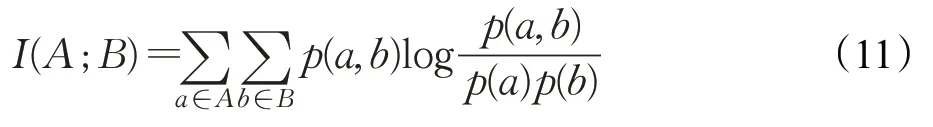
其中,p(a,b)为A、B的联合概率分布函数,p(a)和p(b)分别是A、B的边缘概率分布函数。
对于多标签数据集,Lee等人[44]开发了一种使用多元互信息的多标签特征选择方法。Doquire等人[45]通过考虑标签和特征之间的依赖性,为多标签分类提供了一种基于MI的特征选择方法。不幸的是,这两种方法几乎没有处理选定特征和候选特征之间的条件冗余。Lin等人[46]提出了一种结合MI的基于最大依赖和最小冗余的多标签特征选择算法。但这种方法忽略了标签之间的相关性。文献[47]提出了一种简单快速的多标记特征选择方法EF-MLFS(easy and fast multi label feature selection)。该方法首先使用MI衡量每个维度的特征与每一维标记之间的相关性,实验表明该方法具有良好的分类效果,且无需进行全局搜索,时间复杂度低。但它将冗余性去掉,只考虑了特征与标签之间的相关性。而针对贪婪搜索和启发式搜索方法会陷入局部最优的缺点,Lim等人[48]于2017年提出的一种基于MI与凸优化的方法,改进了以往基于启发式搜索的特征选择策略,在MRMR方法的基础上利用MI计算相关性与冗余性,得到全局最优解,但该方法需要计算所有的一阶依赖关系,因此计算效率不高。针对高阶特征相关性的低阶近似度量缺乏理论基础支撑的问题,文献[49]提出了一种基于联合互信息和交互权重的多标签特征选择方 法MFSJMI(multi-label feature selection method based on joint mutual information),但并没有准确度量候选特征与已选特征关于标签集合的冗余性。针对大多数研究没有考虑到标签的不平衡性,文献[50]提出了一种基于标签不平衡性的多标签粗糙互信息特征选择方法,实验验证了该算法的有效性,但该算法没有考虑特征之间存在的冗余性。
有研究人员将MI推广到模糊互信息上,文献[51]提出了一种基于模糊互信息的多标签特征选择。它考虑的是连续数值的MI。在多标签学习中,假设相关标签均匀分布,会忽略了相关标签之间的差异,导致监督信息的丢失。文献[52]针对此问题提出了一个基于标签分布和模糊互信息的特征选择算法。但上述算法大多没有关注标签之间的共现特性。为了解决这一问题,文献[53]提出了基于标签共现关系的多标签特征选择LC-FS(multi-label feature selection based on label co-occurrence relationship),该算法利用样本标签间的共现关系定义了特征与标签之间的模糊互信息,并结合MRMR实现特征选择。在5个公开数据集上进行了实验,实验结果表明所提算法的有效性,但忽略了标签间的相关性。
也有研究人员将MI推广到条件互信息CMI(conditional mutual information)上,刘杰等人[54]提出一个新的基于条件相关性概念的条件相关特征选择算法CRFS(condition relevance feature selection),验证了条件相关性较传统的相关性具有一定的优势,然而,随着数据特征维数的不断增加,数据间的关系变得越来越复杂,如何客观、快速地找出数据间真实的关系仍是一项艰巨而紧迫的任务。程玉胜等人[55]提出利用CMI将专家特征与其他特征联合并进行了相关性排序,去除冗余性较大的特征,提高算法的性能,但其存在专家特征的选取与个人选取的特征不一致的问题,从而造成结果存在一定的误差。文献[56]提出了一种新的基于CMI的过滤式特征选择方法,该方法通过最大化逼近的全维CMI,并通过建立HSIC的关系,对其内在的相关性最大化和冗余最小化的促进作用进行了定性验证。实验结果表明该方法在标签预测方面具有优势。文献[57]根据MRMR准则,采用类标签与特征集之间的联合互信息和特征集之间的联合互信息来描述关联和冗余,提出了一种基于CMI的最大关联最小冗余特征选择算法CMI-MRMR。实验结果表明,与其他算法相比,CMIMRMR在花费更多时间的前提下,能够获得更好的特征选择性能,但在某些数据集上该方法选取的前50个最优特征的分类精度比所有特征的分类精度差,因此对特征个数的确定需要进行进一步优化。
在多标签数据的标签集合中,每个标签都具有不同的重要性权重,不同权重的标签对选取特征具有重要的影响。一些研究人员就此方面给出了相应的办法。陈福才等人[58]针对标签关系和标签权重,提出了一种基于标签关系改进的多标签特征选择算法MLFSLC(multilabel feature selection algorithm based on the improved label correlation),该算法对特征相关性和冗余性进行了加权,从而选择出最佳特征子集。实验结果表明该算法能够提高多标签学习算法的效率,但是由于互信息量计算方法的限制及算法的处理对象是离散型特征变量,在对具有连续型特征变量的数据集进行离散化处理的过程中,会对数据结构造成破坏,影响分类结果。白伟明[59]提出了一种MI加权标签的多标签I-Relief(iterative Relief)算法,但在选取I-Relief框架处理多标签时,有可能得到局部的最优子集。孟威[60]提出了一种基于相关特征组的多标签特征选择算法CFGFS(multi-label feature selection algorithm based on correlation feature group),该算法根据带有不同重要性权重的标签组,在每个特征组中选取与标签组相关的特征,但该算法仅考虑了特征之间存在的相关性,却没有考虑特征集合中可能存在的某些结构关系,例如特征分层、特征重要性。
大部分基于MI的多标签特征选择方法先是使用MI或者MI的推广衡量特征的重要性和相关性,然后构造搜索策略求解评分函数对所得重要性进行排序选择最优特征子集。该类方法与基于一致性的多标签特征选择方法相比,时间、内存消耗显著减少。并且较其他过滤式方法应用广泛。其中,最优方法不仅考虑了特征与标签相关性强的特征,还考虑了重要性次要的特征以及可能决定整体预测方向的最关键特征,并且它具有较好的稳定性和实际应用价值,去除了冗余性较大的特征,减少了计算时间,提高了分类性能。
③使用MRMR衡量特征与标签的相关性
MRMR是在MI最大化的基础上提出的基于关联和冗余的特征选择算法。它采用特征与类标签之间的MI来描述相关性,利用特征之间的MI来描述冗余。由于同时考虑了相关性和冗余性,提高了这些算法的特征选择性能。MRMR由Peng等人[61]首次在2005年提出,其理论基础为:

其中,D表示独立性R表示冗余性S为选择的特征子集,C为对应的标记。
文献[62]提出了一种过滤式多标签特征选择算法ML-MRMR(multi-label max-relevance min-redundancy),该算法通过对特征进行权重运算,获得特征与多标签集合的关联信息,以得到最优特征子集。文献[63]提出了一种基于MRMR联合MI多标签特征选择算法JMMC(multi-label feature selection algorithm based on joint mutual information of max-relevance and minredundancy),该算法通过使用MI和交互信息的理论以及最大最小的特征选择原则,得到最优子集,并且降低了计算复杂度。文献[64]针对MRMR算法存在的问题,提出一种新的最大相关最小冗余特征选择算法New-MRMR(new algorithm for feature selection with maximum relation and minimum redundancy),该算法在冗余度度量准则方面引入了2种不同的方法,在相关度度量准则方面引入了4种不同的方法,结果表明新提出的方法所选的特征子集更优,当然其他评价冗余度和相关度的方法也可以适用该框架,且这些算法在不同数据集上表现性能不同。文献[65]基于MRMR准则提出一种新的基于相关性与冗余性分析的半监督特征选择方法S2R2(semi-supervised feature selection method based on relevance and redundancy),该方法可以有效识别与移除不相关和冗余特征,提高算法的运行效率,但其在高维数据集中计算复杂度较高。
基于MRMR的多标签特征选择方法与基于MI的方法步骤类似,但该方法不仅考虑了特征之间的相关性和冗余性,还考虑了特征与标签之间的相关性,可以提高分类的准确率,降低特征的维数。其中,最优方法可以有效识别与移除不相关和冗余特征,提高了算法的运行效率,降低了计算复杂度,可以更好地应对大规模特征选择问题,较其他方法性能好且具有泛用性。
④使用HSIC准则衡量特征与标签的相关性
HSIC准则是两组随机变量之间基于核的依赖测度,包括有偏HSIC[66]和无偏HSIC[12]两个版本。给定一组的观察结果D={(x i,y i)}m i=1来自P xy联合概率分布和所选的核函数k和l,可以构造两个核矩阵K,L∈Rm×m,其中K ij=k(x i,x j),L ij=l(yi,y j)。呈现的是如下形式:
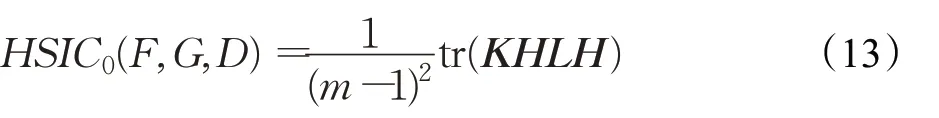
为了解决这一偏差,在文献[12]中提出了无偏估计,其形式为:
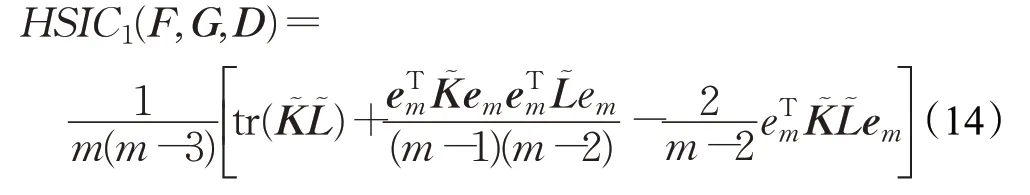
其中,͂和是通过使K和L的对角项为零得到的矩阵,即,这里的δi,j为克罗内克符号。
将HISC应用于特征选择问题时,可以描述所选特征与标签之间的显著相关性。对于候选特征,既要最大化其相关性,又要最小化其最大或平均冗余,文献[67]利用特征空间和标签空间的线性核,提出了一种简单特征排序和顺序前向选择相结合的多标签特征选择方法。但这种方法由于其贪婪搜索策略,只能找到局部最优特征子集。因此,文献[68]提出了一种基于无偏HSIC准则和控制遗传算法的多标签特征选择方法CGAHSIC(multi-label feature selection method combining unbiased Hilbert-Schmidt independence criterion with controlled genetic algorithm),但它没有考虑标签之间的依赖关系。文献[69]提出了一种基于HSIC的最大化依赖性多标签半监督学习方法DMMS(dependence maximization multi-label semi-super vised learning method),该方法选用HSIC作为所有样本特征集和标签集之间的依赖程度的度量,但未考虑标签之间的依赖性。文献[70]提出了一种基于HSIC准则的图数据特征选择,然而使用子图作为特征的方法仍然面临着信息丢失的问题,因为子图有效考虑多个脑区之间的拓扑结构信息,但这种方法对单个脑区的变化不是很敏感,且对病理相关的区域的变化以及怎样的变化导致疾病的发生的问题没有很好的解决。文献[71]提出了一种半监督多标记特征选择算法SSMLFS(semi-supervised multilabel feature selection),通过分析样本特征与其相对应的标记之间的相关性,合理利用未标记数据的信息,但该算法是基于每个数据样本属于正确标记的前提下进行研究的,没有考虑样本误分类的情形且没有考虑成对标记之间的依赖性。为了增强多标签分类器的泛化能力,利用多标签特征选择方法对原始空间进行表征,可以得到近似最优的特子集,Li等人[72-73]提出了两种对连续数据具有Pareto最优性的多标记特征选择方法MLFSPO(multi-label feature selection approach with Pareto optimality for continuous data)和UN-MLFSPO(multilabel feature selection with Pareto optimality without presetting threshold)。不过UN-MLFSPO仅根据Pareto最优性得到最优特征子集,无需预先设定特征数量和阈值。它们都不适合特征少标签多的情况,也没有针对标签间的相关性进行分析。
基于HSIC的多标签特征选择方法以最大化特征与标签之间的相关性为目标,利用HSIC构造特征与标签之间的相关矩阵,然后根据搜索策略与特征排序准则相结合选择最优特征子集。该方法具有较好的分类性能和鲁棒性,尤其在半监督方法上可以合理利用未标记数据的信息进行特征选择。其中,最优方法利用标签加权方法评估标签的重要性,可以有效地处理低维空间中的线性不可分问题,提高了分类的泛化性能和鲁棒性。
(2)考虑了标签间的相关性
现有多标签特征选择算法在选择最优特征子集时较少考虑不同标签之间的相关性对结果的影响。
①使用ReliefF衡量
文献[74]提出了一种用于处理多标签问题的过滤特征加权方法ReliefF-ML,该算法根据特征对近邻样本中同类和异类的感度来选择较优的特征并利用加权特征集进行分类,该方法可以应用于连续问题和离散问题,它包含了特征之间的相互作用,并考虑了标签依赖性。Slavkov等人[75]将HMC-ReliefF与基于BR的特征排序方法进行了比较,实验表明HMC-ReliefF算法表现良好。该算法利用了标签之间的依赖关系,并可扩展到具有大量标签的域,但该算法生成的排名的稳定性对邻域的大小不太敏感。
②使用MI衡量
Li等人[76]设计了一种基于MI的最大关联最小冗余粒度特征选择算法。但当信息颗粒数量很大时,其复杂度较高。Sun等人[77]通过约束凸优化构造了一种基于MI的特征选择算法,通过标签相关性生成广义模型。但上述算法假设标签空间中所有标签的比例相同,忽略了每个标签的比例对特征与标签集的关联度的影响,从而降低了分类性能。基于这一观察,引入每个标签的比例来改善MI衡量变量之间的相互依赖性,它可以表明标签之间的重要性,特征和标签集之间的强度对多标签数据集进行预处理。文献[78]提出了一种基于MI和ML-ReliefF的多标签特征选择方法,以提高多标签分类性能。
传统的基于MI的多标签特征选择算法大多未探讨标签集内在的语义结构,针对以上不足,文献[79]利用标签之间的MI和挖掘出的标签集语义结构信息进一步度量特征和标签集的相关性,再利用MRMR框架筛选特征,实验证明了该算法的有效性,但对于标签个数较少的数据集采用聚类方法可能效果不佳。针对多标签特征选择方法在测量不同特征时忽略了标签关系对特征的不同影响和标签关系的动态变化,文献[80]提出了两种新的多标签特征选择方法,即考虑标签补充的多标签特征选择方法LSMFS(multi-label feature selection considering label supplementation)和考虑最大标签补充的多标签特征选择方法MLSMFS(multi-label feature selection considering maximum label supplementation)。
②使用HSIC准则衡量
在图分类中,在多标签情况下对图数据进行分类的主要困难在于图数据结构复杂,缺乏对多标签概念有用的特征。因此为图数据选择合适的特征集是多标签图分类中必不可少的重要步骤。文献[81]首次将多标签特征选择用于图数据,提出了一种新的图数据多标签特征选择方法gMLC(multi-label feature selection frameworkfor graph classification),该方法可以利用子图特征与图个标签之间依赖性的评价标准gHSIC来寻找最优的子图特征集进行图分类。当然,标签相关性也考虑在内。不过它只使用了简单的策略来构造标签核矩阵,也可以采用各种其他类型的标签核函数来衡量多个标签之间的标签相关性,且该方法只选择一组子图特征并在多个支持向量机上使用。文献[82]根据图的标签之间存在着相关性提出了一种基于HSIC的多标签特征选择算法,并采用交替最优解算法来进行优化。但图的多个标签之间的关联性仍需进一步挖掘,可采用更优秀的核函数替代多项式核函数。
在过滤式算法中,选择一个合适的评价准则可能得到较优的分类效果,但无法保证选择的最优特征子集的规模最小,当特征与分类器存在较大相关性时,找到的最优特征子集规模会更大,冗余和不相关的特征也会增多,很大程度上影响多标签学习的分类性能。但这类算法可以快速剔除大量冗余和不相关特征,运行效率高,适合于大规模数据。
2.2 基于包裹式的多标签特征选择
包裹式算法可以看作分类算法的一部分,它将特征选择过程和分类器封装在一起,根据分类器来评估特征子集的优劣。其主要思想是从特征集合中选择可使学习器性能最佳的特征子集。由于特征子集组合种类随特征个数增加而指数性增长,因此从所有特征组合中进行搜索是一个NP-hard问题。为此一般会选取一些时间复杂度低的搜索策略,例如启发式策略或是进化算法(evolutionary algorithm,EA)等。
2.2.1 采用进化算法的包裹式算法
进化算法也可称为演化算法,遗传算法(genetic algorithm,GA)是进化算法的其中一种。
针对遗传算法的搜索策略,文献[83]提出了一种新的基于标注关键词的图像检索多标签图像标注方法。除此之外还采用了基于PageRank的标注细化方法。文献[84]提出一个混合优化的多标签特征选择算法HOML(hybrid optimization based multi-label feature selection),该方法结合了全局优化能力较强的模拟退火算法和遗传算法及局部优化能力较强的贪婪算法得到最优特征子集。实验证明,该方法有效地降低了数据的维度并较好地提高了分类性能。但并未从根本上解决遗传算法本身缺陷给特征选择带来的不良影响。因此,文献[85]提出了一种基于改进型遗传算法的多标签特征选择算法,该算法通过在模拟退火过程引入Metropolis准则和在遗传算法中引入大变异来获得最优解,但其存在计算效率不高等缺陷。针对遗传算法在识别接近全局最优的特征子集方面存在局限性,导致运行时间长的问题,文献[86]提出了一种适用于多标签分类的模因特征选择算法,防止了早熟收敛,提高了分类效率。但这种方法在对特征进行选择的时候并未考虑标签之间的隐含关联信息,使得到的特征子集并未达到最佳。包裹式方法也可用于多目标,比如文献[87]提出了一种包装型多目标多标签特征选择MMFS(multi-label multiobjective feature selection method)。该方法以多标签最近邻法ML-KNN为基础,进而利用进化遗传算法NSGA-II对平均精度最大化和汉明损失最小化。实验表明,该方法比现有的其他方法具有更好的性能,但还需在更多的数据集上验证和控制所选特征的大小。
针对传统进化算法中的由于初始种群通常是随机产生的造成对输入数据集的知识不可获取的问题,文献[88]提出了一种基于EA的考虑特征和标签之间依赖关系的多标签特征选择方法的初始种群生成方法,这是首次提出一种无参种群初始化方法,该方法可以作为EA的预处理。文中首先引入CMI,设计了一种得分函数计算每个特征的重要度,进而生成初始种群;然后将生成的种群作为基于EA的多标记特征选择方法的输入。该方法提高了传统基于EA的多标记选择方法的分类性能,但该方法需要二次计算,虽然采用了一种低秩近似方法来减少计算问题,但作为种群初始化过程的一部分,在大型特征数据集中选择特征的计算负担仍然很重。
进化算法除了上述算法,还包括其衍生算法多目标演化算法、神经进化算法、差分进化算法、粒子群算法(particle swarm optimization,PSO)等。比如文献[89]提出的一种基于差分进化的多标签多目标特征选择算法,该方法将分类性能和特征数作为适应度函数。文献[90]提出了一种基于PSO算法的包装器多标签多目标特征选择算法。该方法利用基于概率的编码策略来表示每个粒子,使问题适应于PSO算法。为了提高粒子群算法的性能,还加入了自适应均匀变异和局部学习策略,针对基于PSO的离线多标签特征选择方法,文献[91]提出了一种基于PSO的多目标多标签在线特征选择方法,然而,如果在选择的开始就出现了大量的显著特征,那么该方法可能会遭受计算上的困难,并且该方法没有考虑标签之间的依赖性。进化算法中的最优方法可以快速收敛,比随机初始化的种群所需的进化过程更少,较传统的基于遗传算法的多标签特征选择方法提高了分类精度,得到更优的特征子集。
2.2.2 采用启发式搜索的包裹式算法
启发式搜索获得的通常为局部最优解,比较常见的算法有前向搜索法SFS(sequential forward searing)、后向搜索法SBS(sequential backward searing)和增l减r法。
针对标签相关性对特征选择的影响,叶苏荷[92]提出了基于标签相关性和贝叶斯网络分类器链BNCC[93]方法(Bayesian network-based classifier chain method)的多标签特征选择算法BNCC-FS(multi-label feature selection algorithm based on label correlation and BNCC algorithm),该方法采用互信息进行优化评分函数,并利用启发式搜索策略搜索最优的特征子集。实验结果证明了该算法的有效性和可行性,但该算法根据链式的顺序依次选择最优的特征子集,未同时考虑所有标签和所有原始特征之间的复杂关系。文献[94]提出了一种基于启发式搜索的多标签特征选择算法,该算法使用ReliefF去除数据集中的不相关特征,采用启发式算法MFO(moth-flame optimization)进行特征子集寻优,进一步去除数据集中的冗余特征和提高分类器的性能,实验结果验证了该算法的有效性,得到了较好的分类效果。文献[95]提出了一种基于标记相关性的模糊粗糙多标签特征选择方法,该方法通过整合全局和局部标签相关性来衡量标签之间的联系,构建多标签模糊粗糙集模型进行特征选择,进而提出模糊依赖函数来评价特征的重要性和前向搜索策略选择最优特征子集。但该方法容易陷入局部最优解。其中,最优方法考虑了标签间的相关性,具有较好的分类效果和相对较低的时间复杂度。
包裹式算法优点在于特征选择与训练分类器结合时能选择出最优的特征子集,这也说明,选择出的特征子集不适用于其他分类器。然而,包裹式方法的主要缺点是它们通常具有很高的计算成本,并且它们仅限于与特定的算法结合使用。
2.3 基于嵌入式的多标签特征选择
嵌入式方法试图利用前面两种方法的特性,在计算效率和有效性之间取得良好的折衷。嵌入式方法克服了计算的复杂性。在该方法中,特征选择和模型学习同时进行,并且在模型的训练阶段选择特征。嵌入特征选择使用从某些分类器中提取的度量来评估特征子集。
在嵌入式方法中,稀疏正则化被广泛应用,因此分类器归纳和特征选择都安排在单一框架中。可以把特征选择问题看成正则化的系数矩阵稀疏问题,因此,可以通过稀疏权重矩阵W选择特征子集,且l2,1范数可以有效地约束W的行间稀疏、行内稳定,更有利于特征选择。从而有:
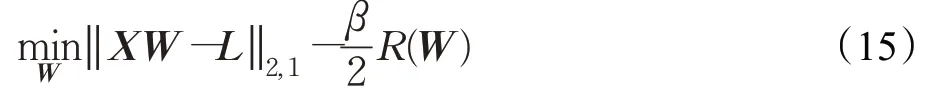
其中,X为特征矩阵,L为标签矩阵,且在l2,1范数距离上有L=XW,第一项为目标函数项,β为惩罚因子,R(W)为正则化项,又为惩罚函数,表示对W的相应约束惩罚
传统的半监督方法主要采用稀疏正则化,但未能充分利用特征与标签之间的关系。文献[96]提出了一种新的基于图的半监督学习框架来解决多标签问题同时考虑多个标签之间的相关性和图上标签的一致性。Chang等人[97]提出了一种有效的半监督特征选择算法CSFS(convex semi-supervised multi-label feature selection),它选择特征不需要图的构造和特征分解。但是,该算法没有考虑到不同标签之间的相关性。然后Chang等人[98]设计了基于标签关联的多媒体标注半监督特征选择FAMLC(semi-supervised feature analysis for multimedia annotation by mining label correlation)。为了更好地利用有限的标签信息来有效地选择特征,文献[99]提出了一种基于稀疏正则化和依赖最大化的半监督多标签特征选择算法FSSRDM(semi-supervised multi-label feature selection based on sparsity regularization and dependence maximization)。该方法利用标记数据和未标记数据来选择特征,同时利用HSIC准则来捕获特征与标签之间的相关性,并采用l2,1稀疏项来获得回归系数稀疏矩阵。实验结果表明,FSSRDM比现有的特征选择方法更有效,但其没有考虑标签之间更复杂的关系来帮助选择重要的特征。
文献[100]提出了一种考虑特征与标签之间共享共模的多标签特征选择方法SCMFS(multi-label feature selection considering shared common mode between features and labels)。该方法可以充分利用特征矩阵和标签矩阵的有用信息来选择信息量最大的特征,但由于SCMFS涉及非负矩阵分解,只适用于非负数据,因此对于混合符号值的数据需要对数据进行非负处理。文献[101]则提出了一种新颖的基于局部标签相关性的共有和类属性特征选择框架,引入l2,1和l1稀疏项同时选取共有和类属性特征,但该方法只考虑了标签之间的正相关性,而没有考虑标签之间的负相关性。针对Zhu等人[102]忽略的特征空间可能是形成标签相关性的一个内在因素的问题,Fan等人[103]提出了一个基于局部判别模型和标签相关性的多标签特征选择方法,但其计算成本较为昂贵,可以专注于基于标签相关性的半监督多标签学习方法。
此外,有研究者将流行学习与稀疏回归相结合,以此来提升算法性能。陈红等人[104]提出了一种基于相关熵和流形学习的多标签特征选择算法CMLS(correntropy and manifold learning feature selection),该方法在目标函数中不但加入了稀疏回归模型而且加入了特征图的正则化,并通过迭代算法解决该问题,实验结果证明了该方法的有效性,其时间复杂度较高。针对正则化项的l1范数、l2范数、Frobenius范数均有自己的局限性问题,且K-Support范数可以在l1范数的稀疏度和l2范数的算法稳定性之间保持平衡的特点,文献[105]提出了基于K-Support范数和流形学习的多标签特征选择算法。文献[106]提出了一种基于流形正则化的嵌入式特征选择方法MDFS(an embedded feature selection method via manifold regularization),用于选择多个类标签共享的判别特征,该方法利用局部标签相关性来增强成对的标签关系,并使用了l2,1范数的正则化。针对大多数多标签特征选择算法都是直接嵌入权重矩阵,很少有对权重矩阵的柔性嵌入,张要等人[107]提出了结合流形结构和柔性嵌入的多标签特征选择算法MFFS(multilabel feature selection based on manifold structure and flexible embedding),但在学习标签相似矩阵时,固定的近邻参数不能够较好地学得标签间的相似矩阵,从而影响了MFFS算法的性能。之后,张要等人[108]又提出了一种柔性结合流形结构与logistic回归的多标签特征选择方法FSML(multi-label feature selection combining manifold learning and logistic regression),但由于近邻参数不能自适应学习,导致同一个近邻参数不一定能够很好地学习到每个数据标签的底层流形结构。从而影响了FSML算法的性能。马盈仓等人[109]针对现有的嵌入式多标签特征选择方法没有充分利用无标签样本的问题,提出一种基于流形学习与l2,1范数的无监督多标签特征选择方法UMLFS(unsupervised multi-label feature selection based on manifold learning andl2,1norms),实验表明该方法的有效性。文献[110]提出一种基于约束回归和自适应谱图流行框架的多标签特征选择方法,并通过实验验证了该方法的有效性,但还需进一步探索如何利用数据的结构化信息。
当然,嵌入式多标签特征选择除了稀疏正则化,还有其他方法,比如:Li等人[111]提出一种新的半监督多标签学习算法COMN(co-training ML-KNN)和PRECOMN(prediction risk based embedded feature selection for COMN),去除了不相关和冗余的特征,但该方法仅说明了半监督多标签学习中的特征选择是可行的,如何应用到无监督学习上还需要进一步探究。Gu等人[112]提出的一种相关多标签特征选择算法CMLFS(correlated multi-label feature selection),但其计算成本较高。You等人[113]提出了一种多标签嵌入特征选择方法MEFS(multi-label embedded feature selection),它采用预测风险准则对特征进行评价,采用向后搜索策略对特征子集进行搜索,选出最有特征子集,它考虑标签相关性,但其特征选择的效率还不是很高。Huang等人[114]提出了一种将稀疏性联合特征选择和多标签分类方法。该方法利用成对的标签相关性学习标签特定特征和共享特征,并在学习到的低维数据表示上同时构建多标签分类器。实验验证了该方法的有效性,但对于大规模数据集时,将要花费大量的时间。其中,在基于嵌入式的方法中,最优方法不仅考虑了标签间的相关性,还引入非负矩阵分解,有利于选择最具区别性的特征,提高了后续特征选择过程的可解释性,并且具有收敛性和较好的分类性能。
与包装器方法相比,基于嵌入式的多标签特征选择方法的计算成本明显更低。这种方法避免了每次探索新的特征选择时对模型的训练。该算法的运行速度较快,但鲁棒性不高。
2.4 几种方法的比较
每种算法都存在自身的优缺点,上述所提出的3种多标签特征选择算法性能总结如表2所示。
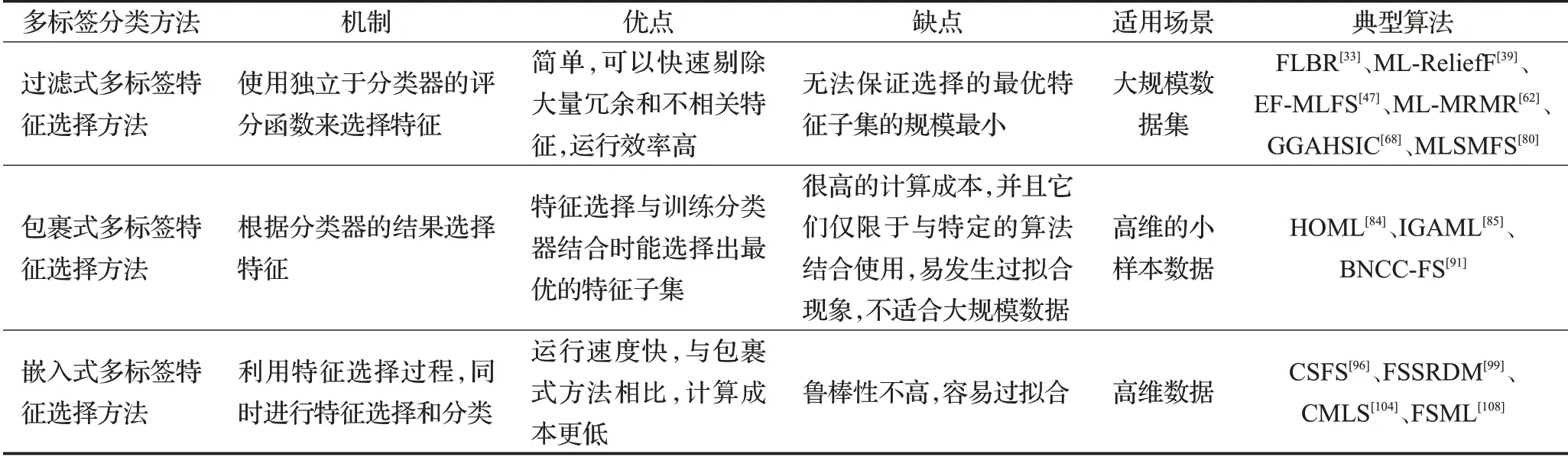
表2 多标签特征选择方法的性能比较Table 2 Performance comparison of multi-label feature selection methods
3 结束语
多标签数据中大量冗余的、不相关的、带噪声的特征,不仅增加了计算的复杂度,还影响算法分类器的性能。多标签特征选择因不仅能够有效地去除冗余特征、不相关特征,还可以保持甚至提高分类器的性能、节省存储空间、缩短分类时间,被成功运用到模式识别、机器学习等领域。然而如何在多标签数据集中选出最优的特征子集是一个十分具有挑战性的事情。本文系统回顾了几种多标签特征选择算法,希望能够为新的实践者和理论者提供有价值的参考,以寻求创新的方法和应用。尽管多标签特征选择算法应用广泛,但仍存在一些问题和挑战有待解决,可以从以下几个方面进行概述:
(1)现有大多数多标签特征选择算法针对于特征空间的相关性和冗余性未进行较多的分析,仅仅考虑了特征间及特征与标签之间的相关性,忽略了不同标签之间的相关性。标签相关性是多标签分类中的一个关键问题,因为根据它从已知标签中导出实例的未知标签是可能的。然而,在多标签特征选择方法中对此问题存在争议。且现有的特征选择算法大都可以删除无关特征并且在一定程度上去冗余,但冗余特征过度删除导致丢失大量信息,比如高维样本数据的去冗余的过程较为复杂,很容易将有价值的特征遗漏,或将冗余特征保留下来。因此如何准确有效地去除冗余特征非常重要。
(2)在单标签和多标签特征选择算法中,另一个开放和具有挑战性的问题是如何确定选择特征的最优数量。对于大多数特征选择方法,要选择的特征数量应该由用户决定。然而,特征的最优数量通常是未知的,并且对不同的数据集是不同的。一方面,选择的特征数量过多可能会增加包含不相关、有噪声和冗余特征的风险。另一方面,由于选择的特征数量太少,一些需要包含在最终子集中的相关特征可能会被消除。因此,更可取的是特征选择算法自动决定最终特征子集的大小。
(3)在多标签特征选择上,过滤式方法大多数情况下较包裹式和嵌入式方法使用更多。虽然过滤式方法是处理大量特征时最合适的方法,但包裹式和嵌入式方法的较高精度不应被忽视。也许可以将它们组合起来[115-117],比如:使用过滤式方法消除不相关的特征,然后使用包裹式或嵌入式方法选择最显著的特征。根据特定的环境选择所需要的度量准则和分类器是也一个值得研究的方向。
