渠道边壁糙率变化对其输水能力影响研究

欧祖贤，杨会朋，王志国，陈力晖，李书芳，3，张亚春

（1.河北工程大学 水利水电学院，河北 邯郸056038； 2.中国水利水电科学研究院北京中水科海利工程技术有限公司，北京 100038； 3.河北工程大学 河北省智慧水利重点实验室，河北 邯郸 056038； 4.河北工程大学 财务处，河北 邯郸 056038）

自然条件的变化和人类活动会使天然明渠渠道输水能力发生变化。 采用河工模型试验可以在分析河流原型的基础上，模拟与原型相似的动力学条件，从而研究河床演变、河道整治等复杂问题。 为使模型阻力与原型阻力相似［1］，模型河床必须达到一定的粗糙程度，而普通的水泥床面往往达不到所需粗糙度，因此需要对其进行人工加糙。 侯志军等［2］通过设计河工模型，分别以梅花形和密排平铺加糙方式对模型进行加糙，结果表明以梅花形布置的糙体糙率比密排平铺糙体糙率大。 朱代臣等［3］通过水槽试验对Y 型加糙体阻力特性进行深入研究，结果表明糙体间距越大，水流阻力越小，且水流阻力的减小幅度随糙体间距的增大逐渐递减并趋于稳定。 已有研究中大多数模型试验是对渠底进行加糙，对边壁加糙并不多见，因此本文在前人研究的基础上，通过对梯形渠道边壁加糙的方式，分析渠道边壁加糙后垂线流速、壁面切应力以及摩阻流速的变化规律，从而剖析渠道边壁糙率变化对其输水能力的影响。

1 模型构建及试验设计

试验梯形渠道长4.000 m、底宽0.350 m、高0.133 m，边坡系数为1.5，梯形渠道由砖砌而成，渠底和边壁采用水泥抹光，在渠道末端安设人字形尾门，通过改变尾门开度来调节渠道水位。 对整个梯形渠道划分20 个断面（编号为cs1～cs20），相邻断面间距为0.2 m，在渠道首部预留1.4 m、尾部预留0.6 m作为过渡段；渠道中部为试验段，长2.0 m，试验段内有10 个测量断面（编号为cs7～cs16），在试验段的渠底和边壁均铺设塑料板，以保证其表面足够光滑。 试验段内每个断面布置5 条测速垂线，从左岸到右岸依次为垂线1—垂线5（其中：垂线3 为中垂线，垂线1 和垂线5 为边壁垂线），干渠横断面垂线布置见图1。

通过设计未加糙试验和加糙试验来对比渠道边壁糙率变化对其输水能力的影响。 在加糙试验中，加糙体尺寸为5 mm×5 mm×6 mm，采用梅花形布置（见图2）并利用双面胶将加糙体粘于渠道边壁，具体分为L＝P＝30 mm 和L＝P＝60 mm 两种糙体间距布置形式，各糙体间横距L和纵距P分别与水流方向平行和垂直。

试验工况见表1，在加糙和未加糙试验中共设置7种流量Q（3、4、5、6、7、8、9 L／s），5 种尾门开度θ（0.0°、7.5°、15.0°、19.0°、23.0°）。 人字形尾门使用时间较长，尾门开度为0°时仍有水流从尾门缝中流出，通过调节流量发现，θ＝0°、Q＝3 L／s 时，水流未溢出渠道；而θ＝0°、Q＝4 L／s 时，水流溢出渠道。 由于电磁流速仪测流速时需满足水深大于3 cm 的条件，为保证渠道内有足够水深且不影响流速的测量，尾门开度为0°时对应的流量设为3 L／s。

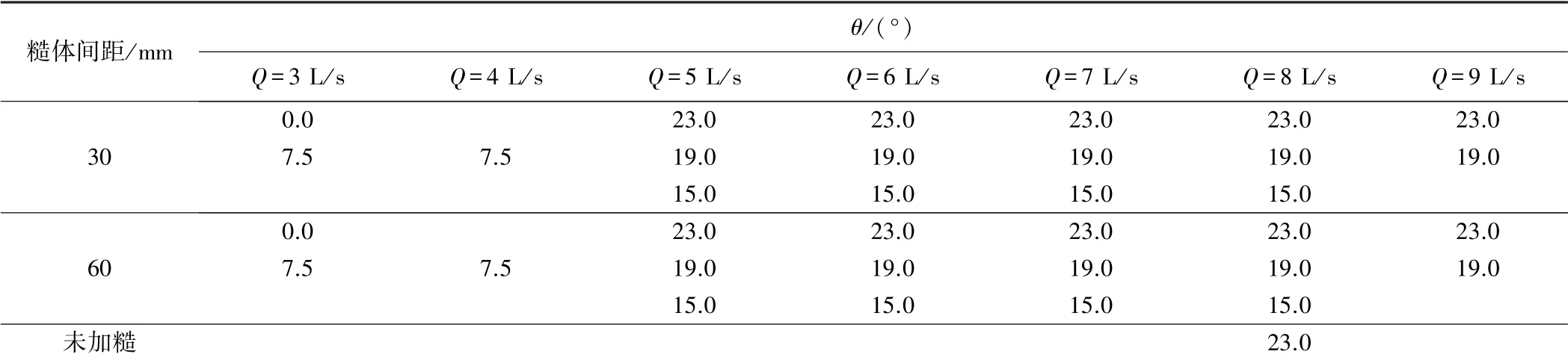
表1 试验工况

2 试验结果及分析

2.1 垂线流速

考虑到试验数据较多，仅选取典型断面cs10 的垂线流速分布进行分析，即对糙体间距为30 mm 时同一尾门开度对应最大流量的垂线流速分布进行分析，见图3（图中纵坐标为垂线上任一点到渠底的距离，横坐标为流速）。

可以看出，垂线3 流速最大，垂线2 和垂线4 流速次之，垂线1 和垂线5 流速最小，原因是水流受渠道边壁糙体阻碍作用的影响较大，垂线3 距边壁糙体最远，垂线1 和垂线5 比垂线2 和垂线4 距糙体更近。 受空气阻力和壅水的影响，同一垂线上水面以下部分流速存在比表层流速大的现象，最大流速出现在水面以下，并且自水面向下第2 个测速点流速最大。 原因是流量和水深一定时，水流分层流经过水断面，而表层流速偏小，水面以下会出现一个较大流速促使水流顺利通过过水断面。 此外，近水面处垂线2 和垂线4 流速与垂线3 流速相差较大，原因是受边壁影响，垂线2 和垂线4 流速小于垂线3 流速，导致水流分离，渠道左右两侧表层出现回流，使垂线2 和垂线4 近水面流速与垂线3 近水面流速差距变大。 从图3 中还可以看出，离渠底最近的测速点流速比垂线上其他测速点流速小，这是由于糙体厚度（绝对粗糙度）为5 mm，糙体影响范围最大值是糙体厚度的10 倍，即为0.05 m，离渠底最近的测速点与糙体的间距小于糙体影响范围最大值，因此糙体影响范围内的测速点流速变小现象较明显。

对未加糙工况下尾门开度为23.0°、流量为8 L／s时cs10 断面的垂线流速分布进行分析（见图4），发现其分布规律与其他工况的垂线流速分布规律不同，最靠近水面的测速点流速为垂线上最大流速，原因是该工况下水深较浅，没有出现壅水现象，导致距渠底越远，流速逐渐增大，表层流速最大。

对同一工况（糙体间距为30 mm、尾门开度为7.5°、流量为4 L／s）cs10 和cs12 断面的垂线流速分布进行对比，见图5。 从图5（c）可以看出，整体上cs12 断面的垂线1 和垂线5 流速分别小于cs10 断面的垂线1 和垂线5 流速，原因是尾门开度小，上游流量大于尾门泄流量时水面壅高，会造成回流现象，而cs12 断面离尾门较近，受回流影响较大。 当流量一定时，由于cs12断面边壁流速偏小，为让水流顺利通过过水断面，同一断面的垂线3 流速应偏大，因此cs12 断面的垂线2、垂线3、垂线4 流速整体大于cs10 断面的流速。 从图5（b）和（c）可以看出，受渠底黏滞力和侧壁糙体的影响，近渠底流速偏小，且自渠底向上第3 个测速点处出现流速拐点，认为是壅水与边壁糙体的交互作用导致该处流速减小。

通常未加糙梯形渠道的垂线流速呈J 形分布［4］，与本试验渠道加糙后的垂线流速分布对比发现，加糙后渠道的垂线流速并不符合J 形分布，特别是垂线2和垂线4 以及边壁垂线上近渠底流速分布不规律。 原因是加糙体布置于渠道边壁上，受梯形渠道边坡的影响，垂线上各测速点与加糙渠道边壁的水平距离不等，近渠底水流受渠底与边壁糙体的综合影响，其垂线流速分布较不规律。

2.2 壁面切应力与摩阻流速

由力平衡方程和能量方程导出的壁面切应力τ0表达式为

式中：ρ为液体密度，kg／m3；g为重力加速度，取9.8 m／s2；R为水力半径，取相邻两个断面的水力半径平均值，m；J为水力坡度，由能量损失计算求得。

采用基于明渠均匀流的阻力平衡原理计算摩阻流速u∗，公式为

摩阻流速和壁面切应力计算结果见表2，可以看出，同一糙体间距和尾门开度下，整体上摩阻流速和壁面切应力随流量的增大而增大；糙体间距和流量一定时，尾门开度越大，摩阻流速和壁面切应力越小；尾门开度和流量一定时，糙体间距为30 mm 的摩阻流速和壁面切应力大于糙体间距为60 mm 的摩阻流速和壁面切应力。 此外，摩阻流速和壁面切应力与糙率呈正相关，加糙后渠道糙率增大，说明水流克服阻力需要的能量增加，导致摩阻流速、壁面切应力增大，从而影响渠道的输水能力。

表2 摩阻流速和壁面切应力计算结果

3 结 论

（1）分析加糙体布置后渠道内cs10 断面的垂线流速分布可知，垂线3 流速最大，垂线2 和垂线4 流速次之，垂线1 和垂线5 流速最小；近渠底流速比其他水深处的流速小。 流量和水深一定时，壅水导致垂线最大流速出现在水面以下；受回流和边壁糙体的影响，垂线2 和垂线4 近水面水流流速与垂线3 的相差较大。 未出现壅水现象时，表层流速最大。

（2）同一尾门开度和流量下，糙体间距越小，摩阻流速和壁面切应力越大。 摩阻流速和壁面切应力与糙率呈正相关，糙率越大，水流克服阻力所需能量越多，从而削弱渠道输水能力。