内蒙古榆树根径与胸径回归关系研究

周志峰,郭 祁,张信杰

(国家林业和草原局林草调查规划院,北京 100714)

目前,我国针对根径与胸径回归关系的研究多涉及针叶树和杨树、刺槐等阔叶树[1-9],涉及榆树的却很少见。本文通过实测内蒙古四子王旗榆树的根径与胸径,筛选出适用性较强的数学模型,确定其应用的最佳范围,以期在今后对内蒙古盗伐、滥伐林木案件进行司法鉴定,以及森林资源管理与监督工作提供科学、准确的依据。

1 研究区概况

四子王旗位于内蒙古自治区中部的大青山北麓,乌兰察布草原西北部。地理坐标为北纬41°10′～43°22′,东经110°20′～113°00′。区域地处中温带大陆性季风气候区,冬季漫长寒冷,多寒潮天气；夏季短促凉爽,降水少而集中,昼夜温差大,日照充足；春秋季气温变化剧烈,大风日数多。年平均气温 1～6℃,无霜期78～142d,年降水量110～350mm,年蒸发量2 300～2 400mm。年平均日照时数3 117.7h,≥10℃积温1 800～3 200℃。年平均风速3.6m/s,风能资源丰富,8级以上大风日数为50d,最高年份达到100d。大风常形成沙尘暴天气使春旱危害加重,也加剧了土壤风蚀沙化速度。

研究区域野生植物较多,有45科225 种。其中以禾本科、菊科最多,豆科、藜科、蔷薇科、百合科次之。主要草本有羊草(Leymuschinensis)、冰草(Agropyroncristatum)、花苜蓿(Medicagoruthenica)、山野豌豆(Viciaamoena)等。灌木树种有柠条(CaraganaKorshinskii)、红砂(Reaumuriasoongarica)、白刺(Nitrariatangutorum)等。天然乔木有白桦(Betulaplatyphylla)、胡杨(Populuseuphratica)、黄榆(Ulmusmacrocarpa)、山杨(Populusdavidiana)等,其中胡杨为世界珍稀树种；人工栽培乔木主要有榆树(Ulmuspumila)、杨树(Populus)、旱柳(Salixmatsudana)等。

2 研究方法

2.1 样本选取与数据采集

样本选取前,根据森林资源管理“一张图”筛选出研究区域优势树种(组)为榆树的森林小班,在此基础上兼顾行政区域和各种立地条件、林分类型(片林、林带)、龄组、郁闭度等抽取不同类型的森林小班作为调查测量的实际地块。在每个地块中选取干形与生长正常的榆树林木作为样木,用围尺测量其根径(D0.05)和胸径(D1.3),并做好记录。根据调查,共实测436株样木,胸径径阶范围为10～22cm。其中,模型参数估计样木共有392株,涉及7个径阶(2cm为1个径阶),各径阶样木株数最多有65株,最少有42株,径阶数量和径阶样木株数均达到《根径立木材积表编制技术规程》[10]规定的径阶范围不少于5个、每个径阶的样木株数不少于40株的要求；模型检验样木44株,均匀分布于每个径阶,以检验模型的适用性。

2.2 模型筛选

首先,根据根径—胸径的散点图推导选出多个拟合程度较好的数学模型。然后,利用SPSS软件或EXCEL估计每个数学模型的各个参数,计算离差平方和(SSR)、相关系数(R)、总相对误差(RS)、相对误差平均值(REA)、相对误差绝对平均值(REAA)、残差(SR),并分析每个数学模型的有效性,选出最佳的数学模型。最后,对选出的数学模型开展F检验,确定其是否适用。相关公式如下:

(1)

(2)

(3)

(4)

(5)

(6)

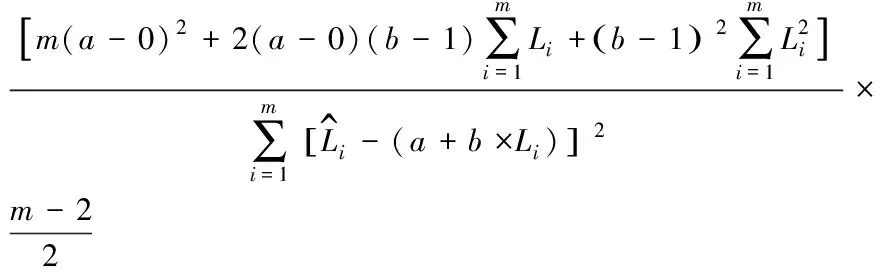
(7)

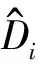
3 结果与分析

3.1 调查结果与分析处理

模型参数估计样木和模型检验样木的调查结果如表1所示。

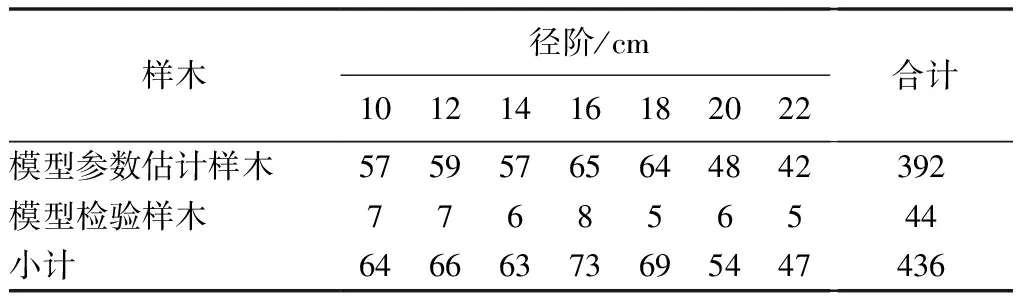
表1 样木统计表

将模型参数估计样木的测量结果以根径(D0.05)为X轴,胸径(D1.3)为Y轴在直角坐标系中绘制散点图(图1),观察每个样木数据在直角坐标系中的分布情况。由图1(a)可以看出:图的右侧和下部有少数样木明显偏离于其他样木,说明这部分样木典型性和代表性不足,应将其作为异常样木从模型参数估计样木中剔除,以保证整个调查结果的合理性和有效性。异常样木被剔除后,模型参数估计样木数量由原来的392株减少为381株,共剔除11株,剔除量占模型参数估计样木总数的2.8%。异常样木占比小于5%,说明本次研究所选取的样木合理、有效。剔除异常样木后的散点图如图1(b)所示。

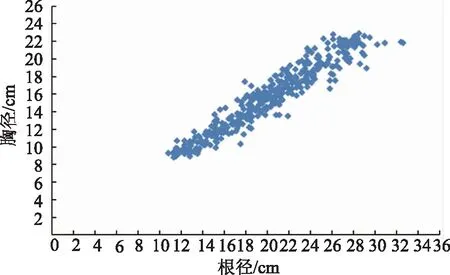
(a)处理前

以剔除异常样木后的381株榆树样木作为根径(D0.05)和胸径(D1.3)数学模型选择和参数估计样本,将样本数据导入SPSS或EXCEL软件,进行拟合试验。参考有关文献[11-13],根据散点图中样木的分布规律,从常用的相关数学模型中选取了拟合程度较好的3种模型,第1种是线性函数数学模型,公式为D1.3=a+b×D0.05；第2种是对数函数数学模型,公式为D1.3=a+b×In(D0.05)；第3种是二次函数数学模型,公式为D1.3=a+b×D0.05+c×D0.052。拟合的同时,通过软件自动计算出每个数学模型的各种参数(常量参数和其他参数)。拟合效果如图2所示。

2.充分发挥E-training 的技术优势，尽可能采用视频、动画或图片等员工喜闻乐见的生动形式，使E-training 内容生动、活泼，充满乐趣，能够吸引员工的眼球，使其乐于打开手机，喜读乐看，爱不释手。总之，应充分发挥E-training 自身优势，在编好课件基础上，通过生动活泼、灵活多样的表达形式，吸引广大员工主动学习、自觉学习，享受学习、培训过程所带来的乐趣，从而做到既能把大家吸引了过来，自觉投入学习培训之中，又能让大家真正看懂、弄通，确保培训效果的提升。

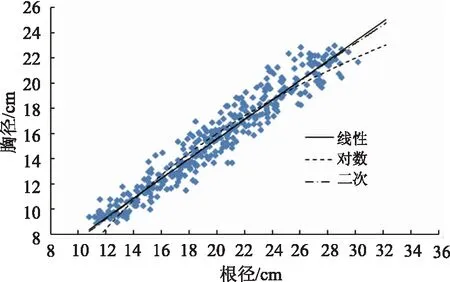
图2 根径-胸径曲线的拟合结果

由图2可以看出:线性函数数学模型和二次函数数学模型的趋势线与各散点的距离上下相对均匀,而对数函数数学模型的趋势线仅在中部与各散点的距离上下相对均匀,越往两端与各散点的距离上下偏差越大。这表明线性函数数学模型和二次函数数学模型的拟合效果明显好于对数函数数学模型,但前两者孰优孰劣,有待进一步评价。

3.2 模型评价

3种根径—胸径数学模型的离差平方和(SSR)、相关系数(R)、总相对误差(RS)、相对误差平均值(REA)、相对误差绝对平均值(REAA)的计算结果如表2所示。

由表2可知:3种数学模型的RS均大于-5%且小于5%,说明此次研究选取的3种数学模型均有效；二次函数数学模型的SSR,R,RS均优于线性函数数学模型和对数函数数学模型,而REA,REAA略低于线性函数数学模型,但优于对数函数数学模,对数函数数学模型相比另2种数学模型而言,在各个指标上明显不占优势。另外,比较残差分布图(图3—图5)可以看出:二次函数数学模型、线性函数数学模型的残差均呈现出以横轴(根径)为中心上下均匀分布,上下相差值仅为0.1,而对数函数数学模型的残差分布上下并不均匀,下半部分明显比上半部分偏离横轴,上下相差值为0.3。

表2 根径—胸径数学模型评价表

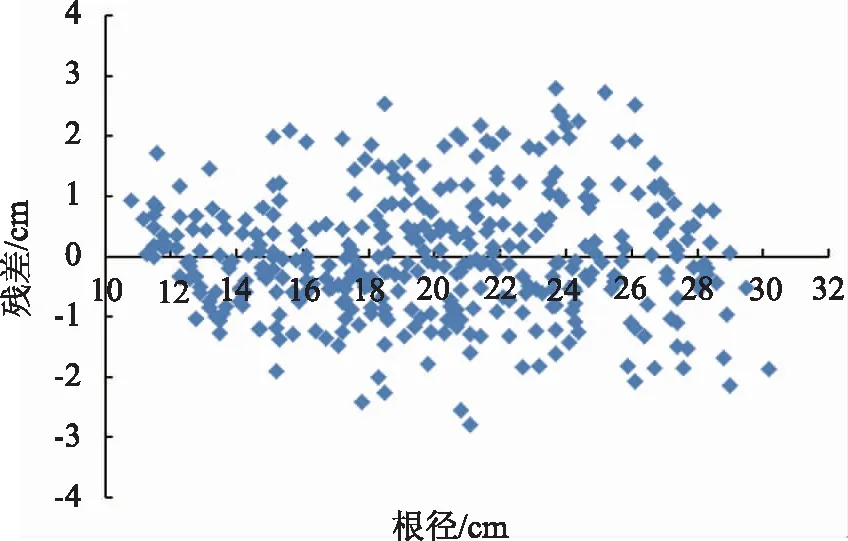
图3 线性函数数学模型的残差分布

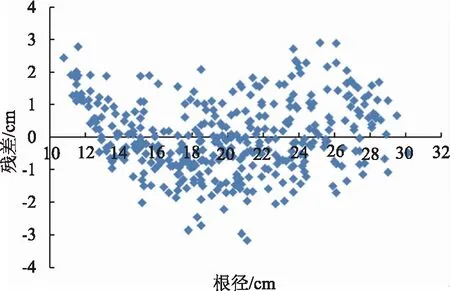
图4 对数函数数学模型的残差分布

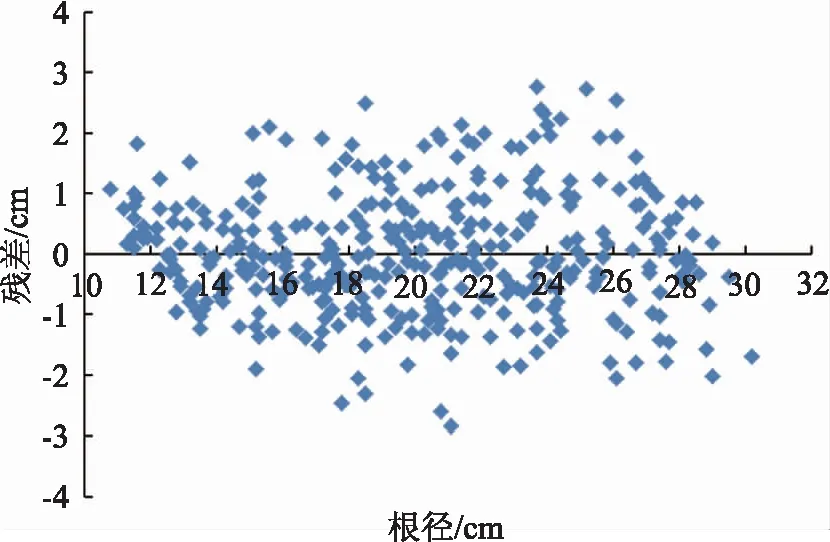
图5 二次函数数学模型的残差分布

综合上述评价,二次函数数学模型相比其他2种数学模型而言,即有效又优秀。因此,将二次函数数学模型作为本次研究的根径—胸径数学模型适用性检验对象,其公式为:

3.3 模型检验

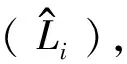
表3 根径—胸径二次函数数学模型检验表

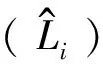
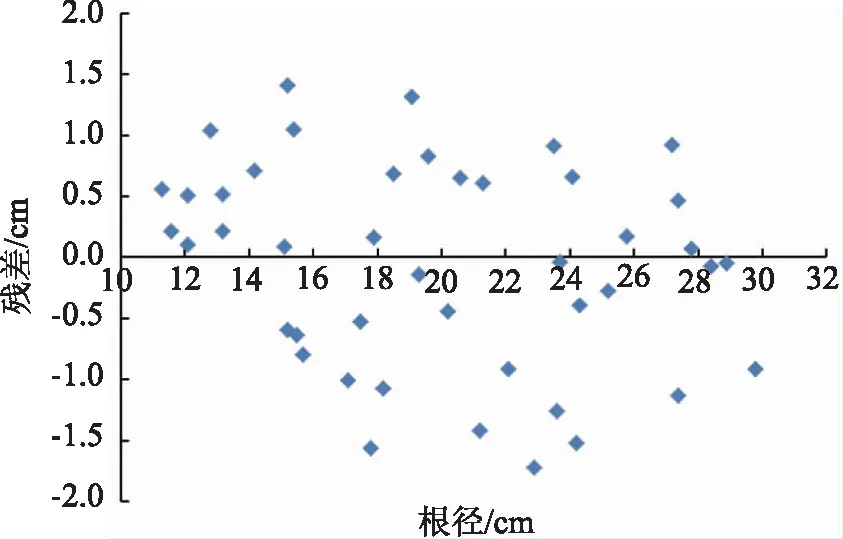
图6 数学模型检验残差分布图

以上说明:本次研究所确定的二次函数数学模型满足各项检验条件,通过适用性检验,能够用于榆树根径向胸径的推算。

4 讨论与结论

4.1 讨论

1)本次研究确定的二次函数数学模型,在拟合的3种数学模型中最优,这与光增云等[4]、顾丽等[6]在其他树种多数学模型比较选择中的结果基本相同,说明研究成果具有一定的科学性和准确性,能够用于榆树根径—胸径回归关系的计算。

2)本次研究成果应用的前提是被盗伐、滥伐、采伐林木的伐根未遭到破坏、保存完好,且有与之对应的胸径一元立木材积表。在依法查处涉及榆树的盗伐、滥伐林木案件时,如果被盗伐、滥伐的林木已不在现场,但留有伐根,那么司法鉴定或技术调查人员可以通过测量被盗伐、滥伐林木的地上5cm处的伐根直径,利用本次研究成果二次函数数学模型计算得出与该根径对应的胸径,再查阅胸径一元立木材积表获得与该林木根径对应的立木材积。如果有当地对应的榆树胸径一元立木材积计算公式,还可将本次研究成果和根径实测值代入该公式中,直接计算得出相对应林木的立木材积。此方法在盗伐、滥伐林木案件中,现场只留有伐根的情况下,推算蓄积量时得到广泛应用[14-16]。除此之外,还能应于林草主管部门对林木采伐利用和森林抚育的监督管理工作,如，检查伐区作业质量、审核采伐林木蓄积、检查采伐限额，以及估计风折木、雪折木、材积等[17],这对森林资源的保护和森林经营具有重要意义。

3)利用本次研究成果计算被盗伐、滥伐、采伐榆树的蓄积量也具有一定的局限性。在其伐根受损、被挖情况下,则不能按照本次研究成果和常规方法计算被毁(伐)林木立木蓄积。此时,可以按照《国家林业局关于毁林案件中被毁坏林木及其伐桩灭失的立木蓄积测算有关问题的复函》[18]规定,根据相应的森林资源“一类”清查数据、“二类”调查数据、森林资源管理“一张图”数据等计算确定；没相应资料的,可以按照国家有关技术规程的规定由司法鉴定人员或技术调查人员在与被毁坏(采伐)林木相同起源、相同优势树种(组)、立地条件和林分生长状况相近似的其他林分内设置标准样地,测量样地内树高、胸径等因子,测算单株、单位面积蓄积量后推算与被盗伐、滥伐、采伐林木株数或面积相应的蓄积量,以此作为刑事立案的依据。

4.2 结论

1)研究结果表明,四子王旗榆树根径(D0.05)和胸径(D1.3)存在着明显的线性关系,通过对榆树根径—胸径的线性、对数、二次3种函数数学模型的比较,得出二次函数数学模型适用性高,公式为:

2)研究得出的四子王旗榆树根径(D0.05)和胸径(D1.3)的二次函数数学模型,适用于人工起源的榆树林,根径最佳适用范围为10～30cm,且在被盗伐、滥伐、采伐数量较大情况下使用时精度会更高。因为被伐林木中包括了不同大小和削度的树木,其正负误差会基本抵消[19]。对于超出此范围或单株林木而言,则可能会出现较大偏差,使用时应慎重。