缝洞型碳酸盐岩储层水力裂缝扩展机制
2022-08-09金仁才
师 访 王 瀚 金仁才
(1. 淮阴工学院机械与材料工程学院,江苏 淮安 223003;2. 中国十七冶集团有限公司,安徽 马鞍山 243000)
0 引 言
碳酸盐岩储层在世界范围内广泛存在[1-2],这类储层含有大量不同形状和尺寸的岩溶缝洞,其中孔洞(溶洞、溶孔等)可为油气提供储存空间,天然裂缝可为油气开采提供有效通道,具有较大的开采潜力。水力压裂技术是油气开发的关键技术之一,其目的是建立开采井与孔洞之间的流动通道,因此压裂过程中应尽可能使得水力裂缝朝着孔洞扩展并形成有效贯通[3]。由于相关实验难以开展,因此借助数值仿真方法开展缝洞型储层水力裂缝扩展机制研究具有重要意义。
近年来随着计算机技术的不断发展,研究人员利用有限元法(FEM)[4]、不连续位移法(DDM)[5]、 相 场 法[6]以 及 扩 展 有 限 元 法(XFEM)[7-9]等不同方法针对水力压裂问题进行了相关研究。其中,针对水力裂缝和天然裂缝相互作用问题,国内外学者开展了大量研究[10-11],研究结果表明:水力裂缝和天然裂缝交会后,根据天然裂缝类型、材料参数以及地应力水平不同,可能会直接穿过天然裂缝形成十字形交叉、终止扩展、T 型或L 型交叉等。由于孔洞周围存在显著的应力集中效应,缝洞型储层水力压裂与常规水力压裂具有显著区别,其裂缝扩展受到孔洞尺寸、地应力水平、地应力差、压裂参数、储层物性参数等多种因素的影响,其裂缝−孔洞交互作用机制较为复杂,目前针对该类问题的水力压裂研究开展得较少。Z.Liu 等[6]基于相场法研究了填充型溶洞对水力压裂的影响,发现裂缝扩展路径与岩石孔洞填充物弹性模量比、孔洞和裂缝的相对位置以及应力水平相关。L.Cheng 等[9]通过扩展有限元法研究了孔洞位置和地应力差对水力裂缝扩展路径的影响。Z.Luo 等[12]建立了流固耦合数值计算模型,研究了孔洞内流体压力对水力裂缝扩展路径的影响,发现较高的流体压力能够减弱水力裂缝的偏转程度。此外,王毓杰等[13]利用单元劈裂法研究了地应力差对缝洞型储层水力压裂效果的影响。
尽管国内外学者开展了一些水力裂缝、天然裂缝和孔洞相互作用机理的相关研究,但相比常规储层,学术界仍然缺乏针对碳酸盐岩储层水力压裂问题的系统化研究,对影响缝洞型储层水力压裂效果的关键因素的认识还不够清晰。为此,本文采用T.Belytschko[14]提出的扩展有限元法描述裂缝和孔洞周围的位移场、水力裂缝和天然裂缝的交叉以及裂缝和孔洞的贯通情况,从而避免裂缝扩展之后繁琐的网格划分过程[8]。在构建流固耦合模型时,采用雷诺方程[7]描述裂缝内压裂液的层流流动,用有限元法对流动控制方程进行离散化处理,最后结合Newton−Raphson 迭代求解流固耦合方程[8],获得节点位移(包括常规节点和增强节点)以及裂缝流体节点压力。本文将通过多个算例研究缝洞型碳酸盐岩储层中水力裂缝扩展机制,找出影响水力裂缝扩展的关键参数,为相关压裂设计提供参考。
1 数值计算模型
考虑含有水力裂缝ΓHF、天然裂缝ΓNF以及孔洞的计算域Ω,Ω 的边界记为Γ,Γ 的外法线为nΓ。边界Γu和Γt分别施加有固定约束和外载荷t。以压裂液注入点为原点,沿裂缝扩展路径定义坐标系s。压裂液视作不可压缩牛顿流体。假设裂缝为准静态扩展[15],孔洞为规则的圆形,孔洞内部无填充物。
1.1 控制方程
根据线弹性假设,岩体变形的控制方程[8]为
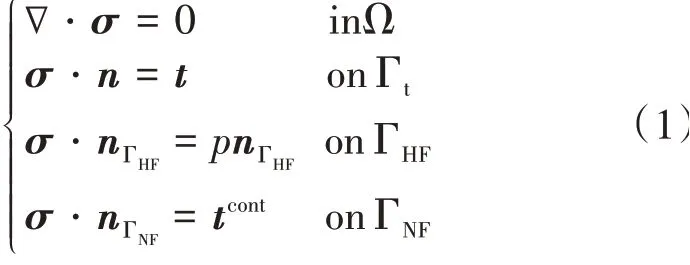
式中:σ——应力张量;tcont——裂缝面接触力,MPa;p——水力裂缝内的流体压力,MPa;nΓHF——水力裂缝的法向量;nΓNF——天然裂缝的法向量。
裂缝内流体流动采用雷诺方程进行描述[8,15],即
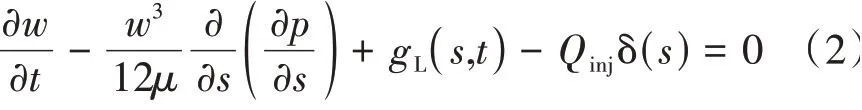
式中:w——裂缝宽度,m;t——时间,s;μ——流体黏度,mPa·s;gL——压裂液滤失量,m/s;Qinj——压裂液注入速率,m2/s;δ(s)——狄拉克函数。
其中,gL的表达式为
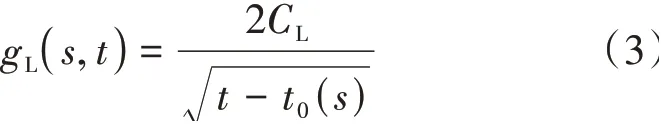
式中:CL——滤失系数,m/s1/2;t0(s)——s点发生滤失的时间,s。
裂缝宽度w的表达式为

式中 [[u]]——裂缝面两边的相对位移,m。
引入试函数u(x,t)和权函数δu(x,t)可得式(1)的等效积分弱形式为
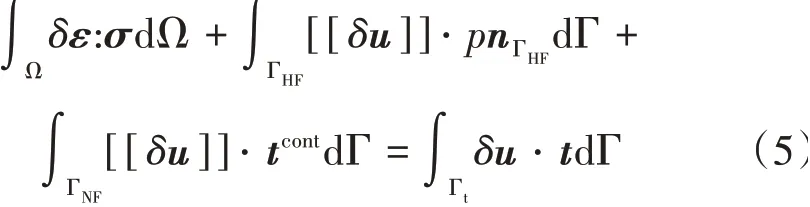
引入权函数δp(s,t)并分部积分,可得式(2)的等效积分弱形式为
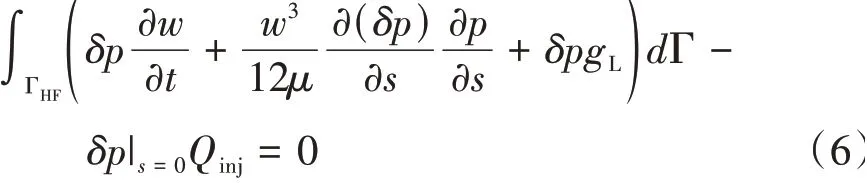
1.2 扩展有限元模型
通过引入额外的自由度,扩展有限元方法可以有效避免常规有限元方法不断划分网格、裂尖网格加密以及新旧网格间的数据映射等操作,从而显著降低问题复杂度和整体计算量[16],特别适合含有复杂裂缝、孔洞结构的水力压裂问题仿真。对于本文所述缝洞型储层,计算域Ω 内任意点x处的位移关系式为
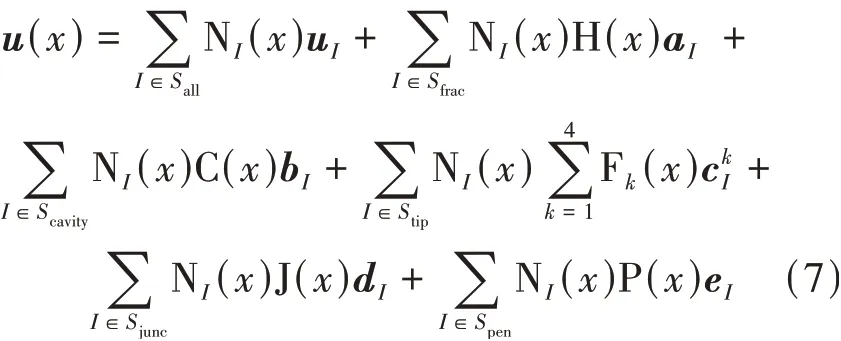
式中:NI——节点I的形函数;Sall——由全部常规节点和增强节点组成的集合;uI——常规自由度向量;Sfrac——裂缝面增强节点;Scavity——孔洞增强节点;Stip——裂尖增强节点;Sjunc——Junction 增强节点;Spen——缝洞贯穿增强节点;aI——Sfrac对应的增强自由度向量;bI——Scavity对应的增强自由度向量;cI——Stip对应的增强自由度向量;dI——Sjunc对应的增强自由度向量;eI——Spen对应的增强自由度向量;H(x)——裂缝面增强函数,其取值与符号距离函数一致,即在裂缝面一侧取值为1,另一侧取值为−1;C(x)——孔洞增强函数,在孔洞内外分别取值为0 和1;Fk(x)——裂尖增强函数;J(x)——Junction 增强函数,根据点x位置不同分别取值1、−1 和0[8];P(x)——缝洞贯穿增强函数,如图1 所示。
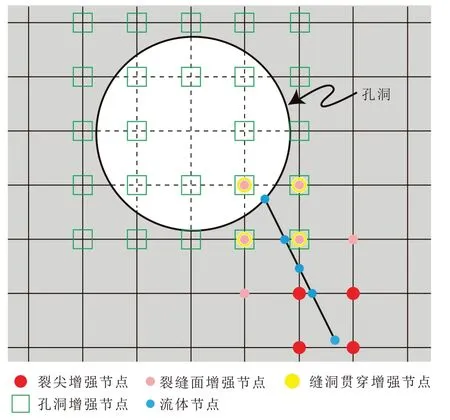
图1 缝洞贯穿型增强示意Fig.1 Sketch of enriched fracture-cavity penetrated nodes
Fk(x)的表达式为[16]
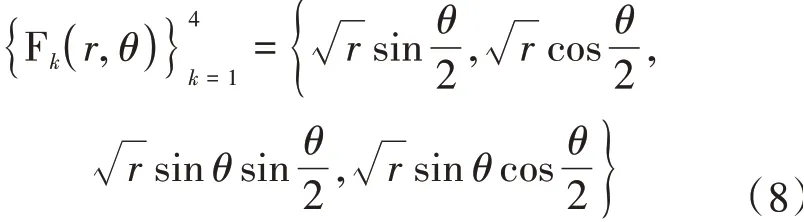
式中:(r,θ)——裂缝尖端位置的极坐标系[17];r——裂缝尖端位置的极坐标系半径分量,m;θ——裂缝尖端位置的极坐标系角度分量,rad。
P(x)表达式为
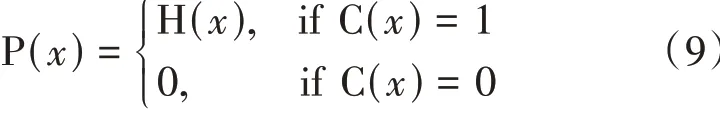
1.3 摩擦型天然裂缝
摩擦型和胶结型是储层中2 种常见的天然裂缝类型[18],本文考虑摩擦型天然裂缝,裂缝面摩擦滑动条件[19]为
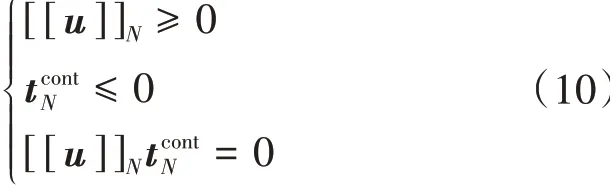
式中N——法向分量。
根据库伦摩擦定律,裂缝面接触状态的关系式[19]为
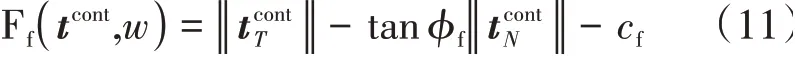
式中:T——切向分量;φf——摩擦角,rad;cf——黏结强度,MPa。
若Ff小于0,裂缝面处于粘结状态;若Ff等于0,裂缝面发生滑动。
1.4 裂缝扩展准则
采用最大周向拉应力准则判断裂缝是否扩展并确定裂缝扩展方向[7],等效应力强度因子计算公式为
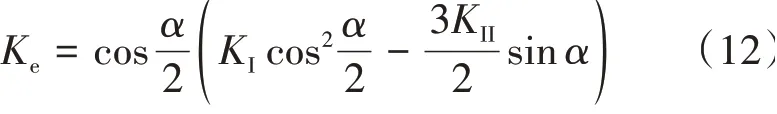
其中
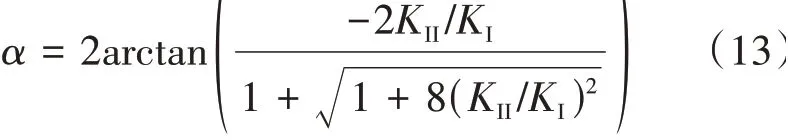
式中:Ke——等效应力强度因子,MPa·m1/2;KⅠ——Ⅰ型应力强度因子,MPa·m1/2;KⅡ——Ⅱ型应 力 强 度 因 子, MPa·m1/2;α—— 裂 缝 偏 转角,rad。
若Ke大于储层断裂韧度KIC,则裂缝将发生扩展,且扩展方向相对于原裂缝的偏转角度为α。本文采用互作用积分法计算应力强度因子[16],同时采用Renshaw−Pollard 准则描述水力裂缝和天然裂缝交互行为[18]。
2 模型验证
利用Fortran 语言编写了扩展有限元程序PhiPsi并用于算例研究。对于考虑天然裂缝的算例,程序执行中需要调用两层Newton−Raphson 迭代循环,外层循环用于求解流固耦合方程(式(1)及式(2)),内层循环用于确定裂缝面接触状态[8]。
本文建立的流固耦合模型在不考虑孔洞的情况下已经经过了充分的验证[7-8,18],为了进一步验证所建立的模型的缝洞交互仿真能力,建立如图2所示的平面应变模型。模型底部固定,顶部受到大小为5 kPa 的拉应力σ作用,几何参数H、h1、h2、l、b1、b2以及a分别取为3.0、1.5、1.0、0.1、1.2、0.7 和0.2 m。弹性模量E和泊松比ν分别取为30 GPa 和0.2。模型总共划分了3 400 个尺寸为0.03 m×0.03 m 的4 节点四边形单元。裂缝扩展增量为0.045 m,扩展15 步后水力裂缝和孔洞贯通。贯通后模型竖直方向位移云图以及增强节点如图3所示(变形放大系数为200),其中缝洞贯通增强节点共有6 个。N.T.Nguyen 等人[20]采用无网格伽辽金法研究了该问题,获得的裂缝扩展路径如图4虚线所示,本文计算结果如图4 实线所示,对比可见二者吻合度极高,说明本文建立的扩展有限元流固耦合模型能够有效模拟缝洞交互作用问题。
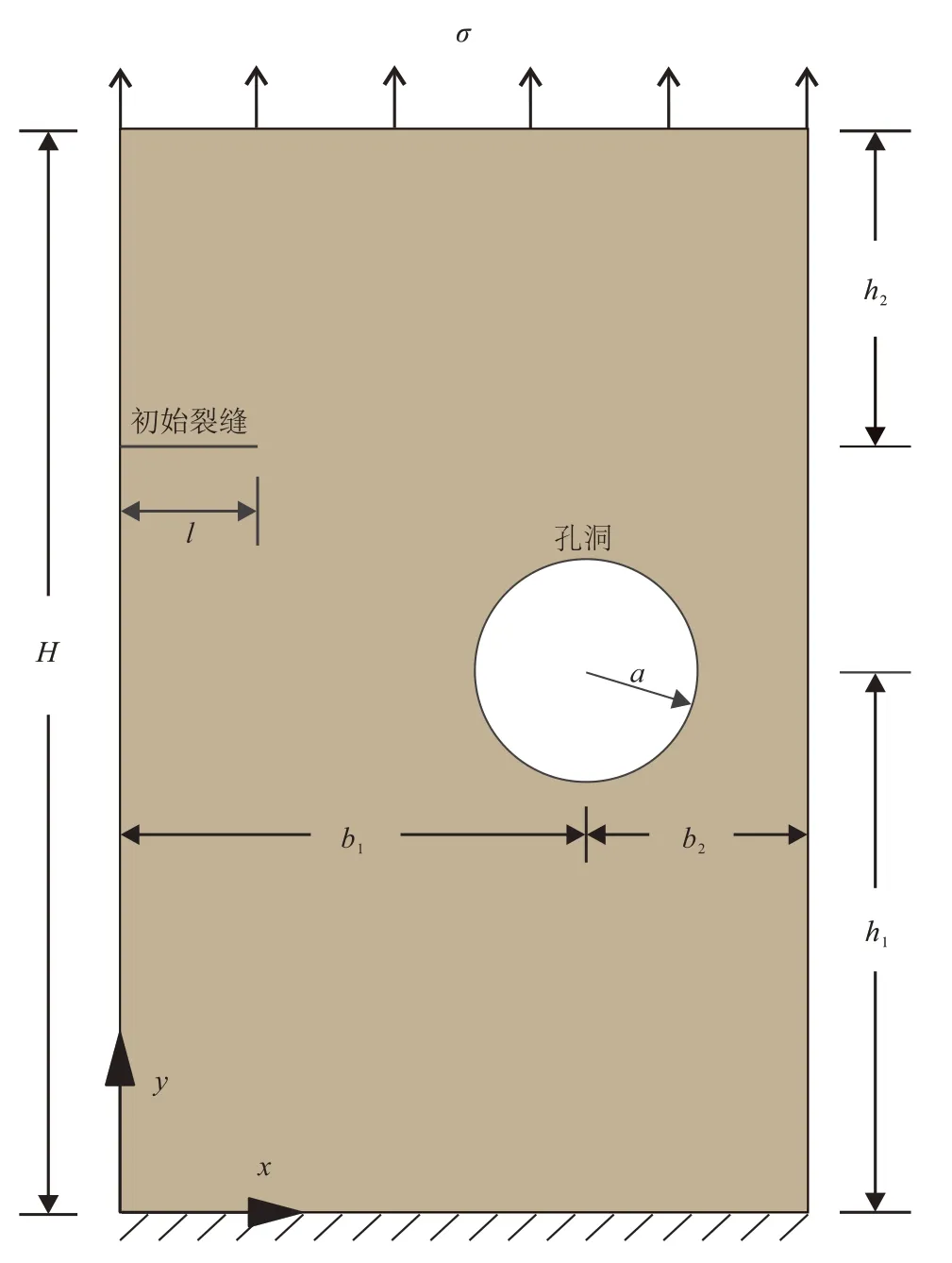
图2 验证算例模型示意Fig.2 Sketch of the model to validate simulation case
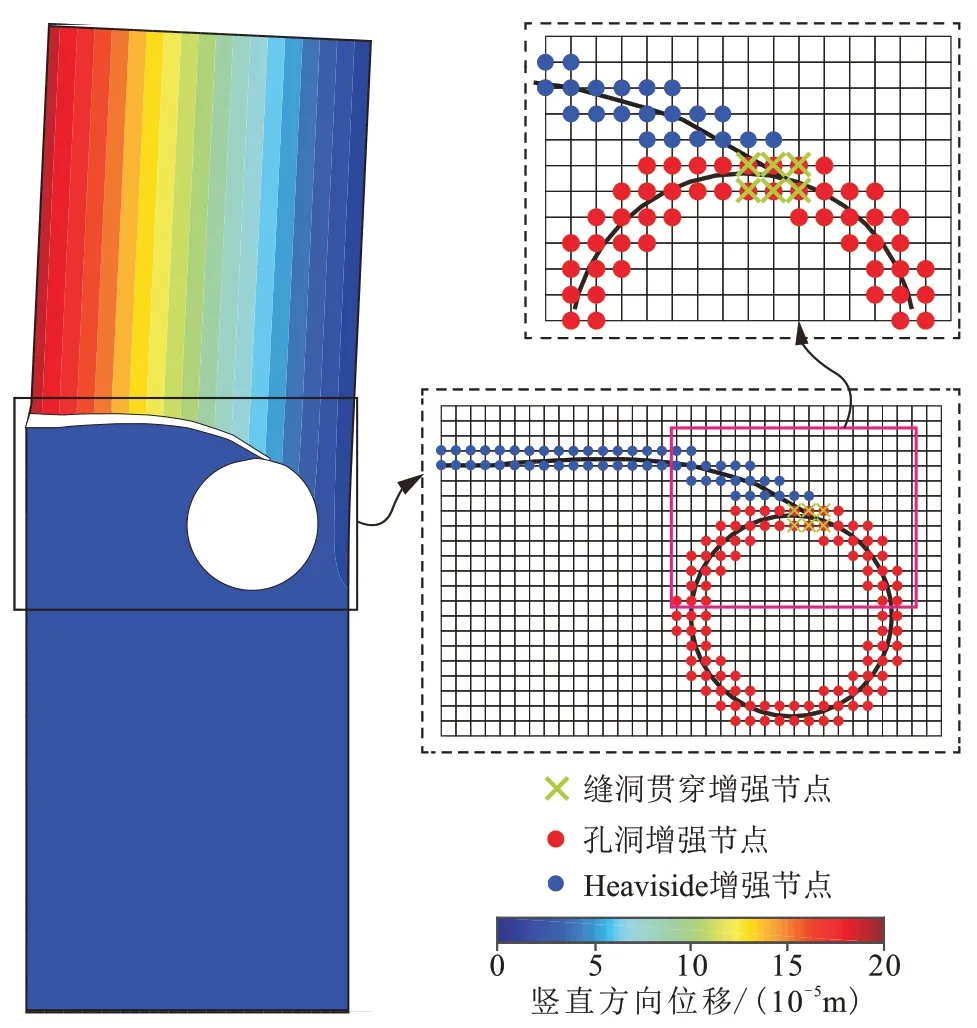
图3 竖直方向位移云图及增强节点示意Fig.3 Sketches of vertical displacement cloud chart and enriched nodes
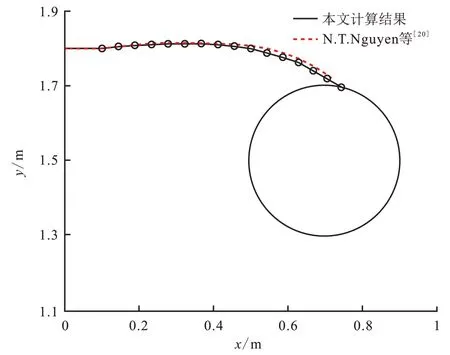
图4 验证算例裂缝扩展路径Fig.4 Propagation paths obtained in validated simulation cases
3 结果与讨论
3.1 水力裂缝和孔洞相互作用仿真
通过平面应变模型(图5),系统研究地应力大小、地应力差、压裂液黏度、压裂液泵注排量、孔洞尺寸以及天然裂缝等对水力裂缝和孔洞相互作用行为的影响。模型尺寸为5 m×10 m,初始裂缝长度为0.5 m,基本算例孔洞半径为0.5 m,孔洞圆心与初始裂缝之间的距离d为0.25 m,地应力σh和σH分别为40 MPa 和50 MPa(侧压力系数λ=0.8)。储层的弹性模量E=30 GPa,泊松比ν=0.2,断裂韧度KIC= 1.0 MPa·m1/2。此外,压裂液黏度μ= 10 mPa·s,压裂液泵注排量Qinj为0.001 m3/s,压裂液滤失系数CL为10−5m/s1/2。模型总共划分成5 618 个4 节点四边形单元,水力裂缝扩展步长取为0.15 m。
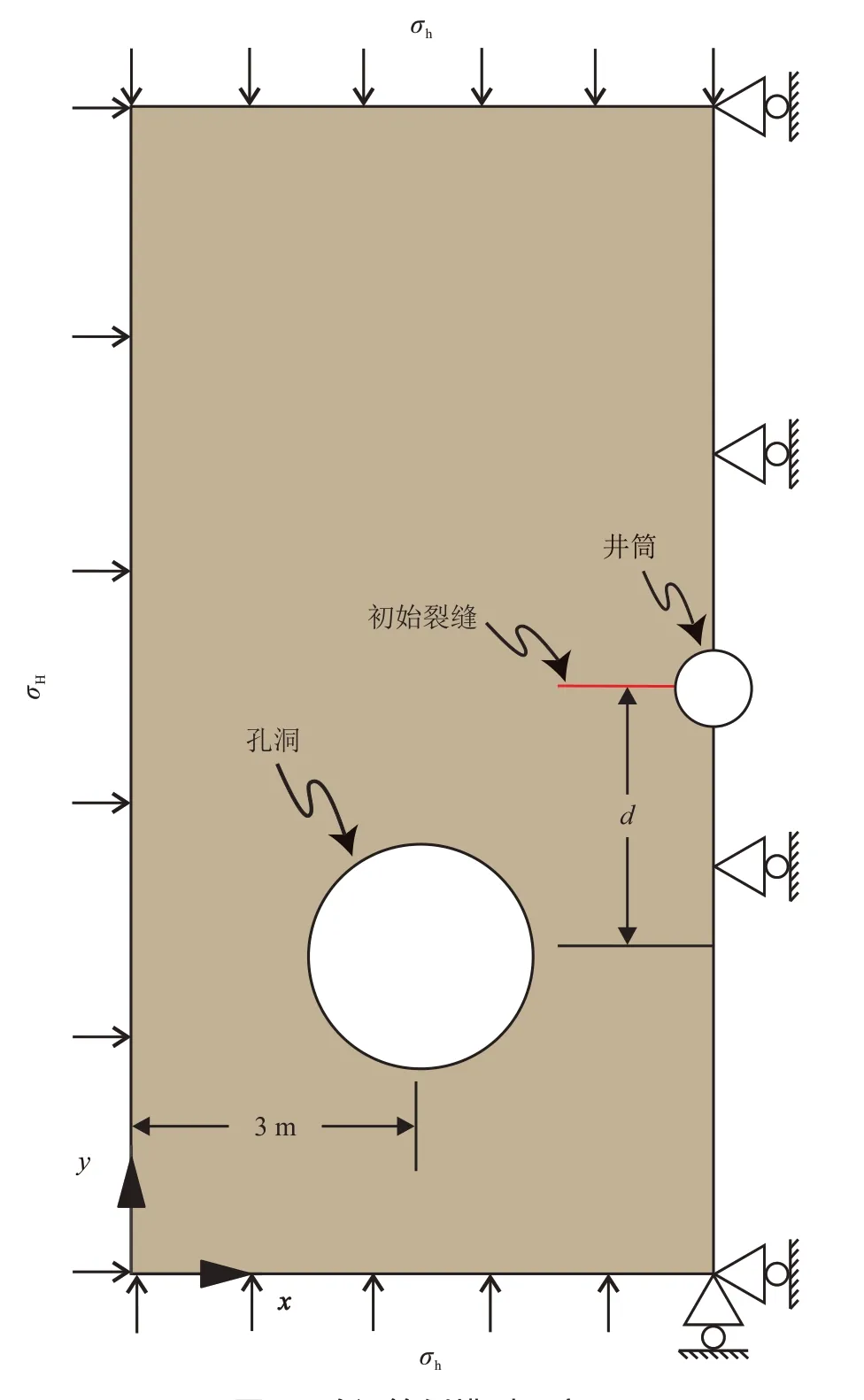
图5 验证算例模型示意Fig.5 Sketch of the model to validate simulation case
裂缝扩展路径和y方向的应力分布情况如图6所示。显然,由模型对称性可知,若不存在孔洞则裂缝将沿着水平方向向左扩展。然而,受到孔洞应力场的影响,天然裂缝扩展过程中绕过孔洞,最终形成弯曲路径。图7 给出了存在和不存在孔洞2 种情形下的井筒注水压力变化曲线,初始扩展阶段受到孔洞右边y方向高应力区的影响,相比无孔洞的情形裂缝扩展需要更大的泵入压力,当裂缝到达孔洞上部低应力区后,所需泵入压力显著下降。
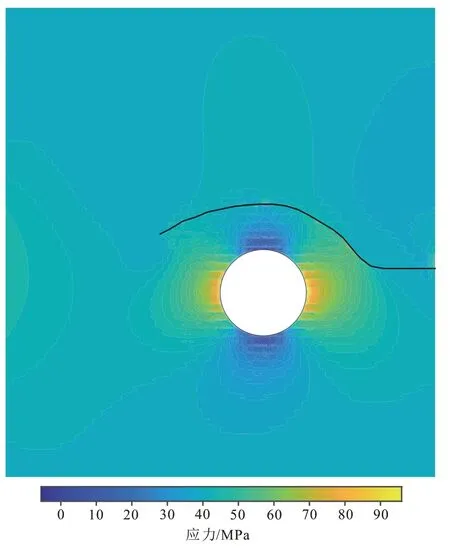
图6 水力裂缝扩展路径及y方向应力云分布Fig.6 Propagation path of hydraulic fracture andstress cloud distribution in y-direction
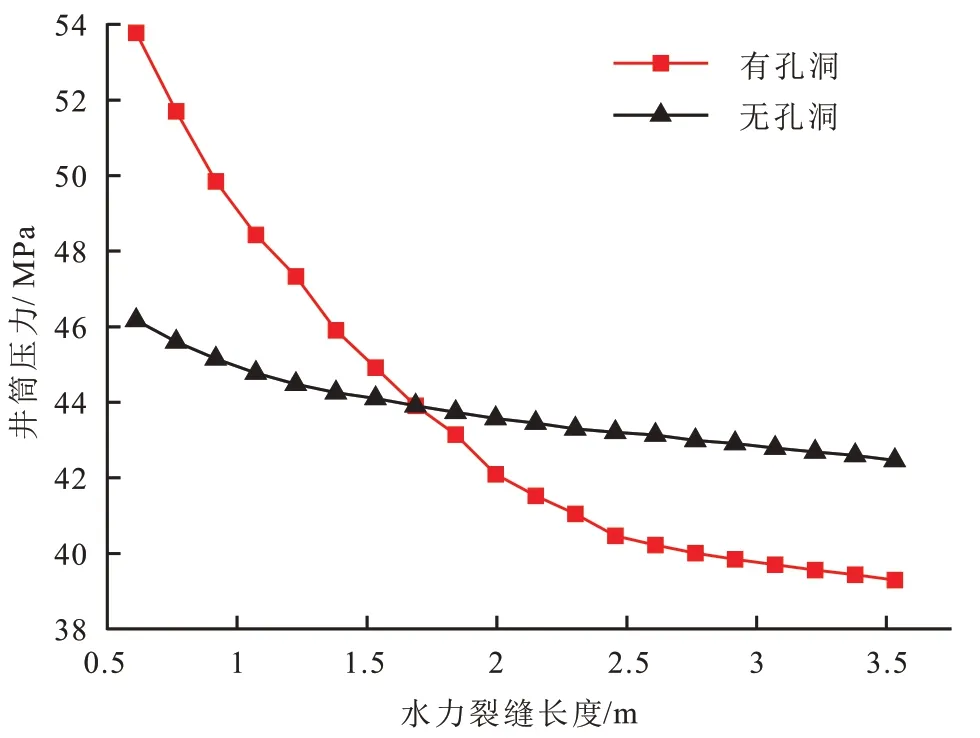
图7 孔洞对裂缝扩展过程中井筒泵注压力的影响Fig.7 Influences of cavity on injection pressure in the process of fracture propagation
3.1.1 地应力的影响
如表1 所示,考虑3 种地应力组合,分别记为算例1、算例2 和算例3。算例1 地应力取值较大;算例2 地应力差取值较大;算例3 与算例2 侧压力系数一致,但地应力差取值较小。计算结果如图8所示,从图8 中可以看出,地应力水平、侧压力系数以及地应力差均会对裂缝扩展路径产生重要影响:侧压力系数越大,孔洞对水力裂缝的影响越大,裂缝扩展路径弯曲程度也就越大;地应力水平或地应力差越小,孔洞对水力裂缝的影响也就越小,水力裂缝能够基本保持初始扩展方向,更容易与孔洞发生交汇贯通。

表1 地应力参数Table 1 Parameters of in-situ stresses
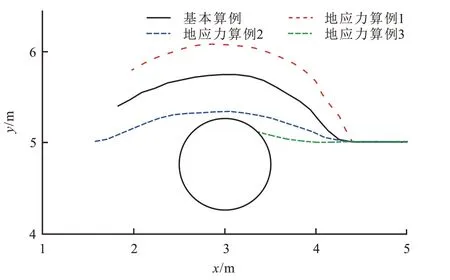
图8 地应力对裂缝扩展路径的影响Fig.8 Effects of in-situ stress on fracture propagation paths
3.1.2 压裂液的影响
压裂液类型(如滑溜水、交联压裂液等)以及泵注排量是水力压裂技术中的关键设计参数。为此,通过2 个算例分别将压裂液黏度从10 mPa·s提高到100 mPa·s,将泵注排量从0.001 m3/s 提高到0.01 m3/s,计算结果如图9 所示。从图9 中可见,提高流体黏度可以降低孔洞对裂缝扩展路径的影响。主要原因在于,采用高黏度压裂液时缝内流体压力较高[21],较高的流体压力可弱化孔洞附近的应力集中效应。从图9 中还可以看出,提高泵入流量可以得到更加平滑的裂缝扩展路径,即能够减弱孔洞对裂缝扩展路径的影响,有利于水力裂缝沿着其原始方向扩展。实际上,根据KGD模型解析解[21]可知,提高泵注排量同样会导致缝内流体压力升高。
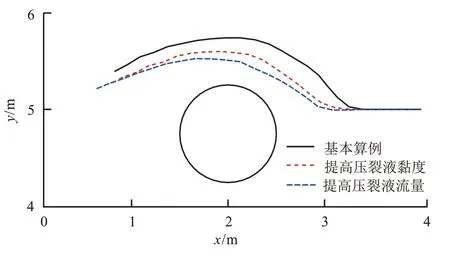
图9 流体黏度和泵注排量对裂缝扩展路径的影响Fig.9 Effects of fluid viscosity and fluid pumping rate on fracture propagation paths
3.1.3 孔洞尺寸的影响
通过半径为0.3 m 的较小孔洞研究了孔洞大小对水力裂缝扩展路径的影响,图10 为计算结果。对于较小尺寸的孔洞,与半径为0.5 m 的基本算例相比,其对水力裂缝扩展路径的作用明显减弱。
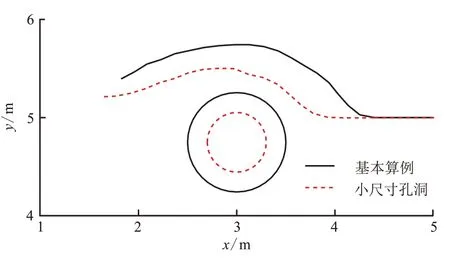
图10 孔洞尺寸对裂缝扩展路径的影响Fig.10 Effects of cavity size on fracture propagation paths
3.1.4 天然裂缝的影响
为了研究孔洞附近天然裂缝对水力裂缝扩展路径的影响,将图11 所示的4 种情形,分别记为算例(a)、(b)、(c)、(d)。图中的天然裂缝初始长度为0.6 m,方向与孔洞法线方向相同,裂缝面的摩擦角为π/6、黏结强度为0.5 MPa。图11(a)、(c)中的天然裂缝与孔洞处于连通状态,而图11(b)、(d)中的天然裂缝未与孔洞连通,天然裂缝顶点与孔洞边缘的距离为0.05 m。图11(a)、(b)中天然裂缝与x轴正方向之间的夹角是−π/4,图11(c)、(d)中该夹角为π/4。计算结果如图12 和图13 所示。可见天然裂缝和孔洞贯通状态与否是决定裂缝扩展路径的关键因素:若天然裂缝和孔洞已贯通,则孔洞对天然裂缝扩展路径的影响更加明显;若天然裂缝和孔洞未贯通,由于天然裂缝面不发生滑动,天然裂缝周围应力场受影响较小,因此孔洞对天然裂缝扩展路径的影响与不存在天然裂缝时差别不大。需要指出的是,图13(d)由于水力裂缝与天然裂缝相遇并终止扩展,故交会点处形成了T 型交叉。
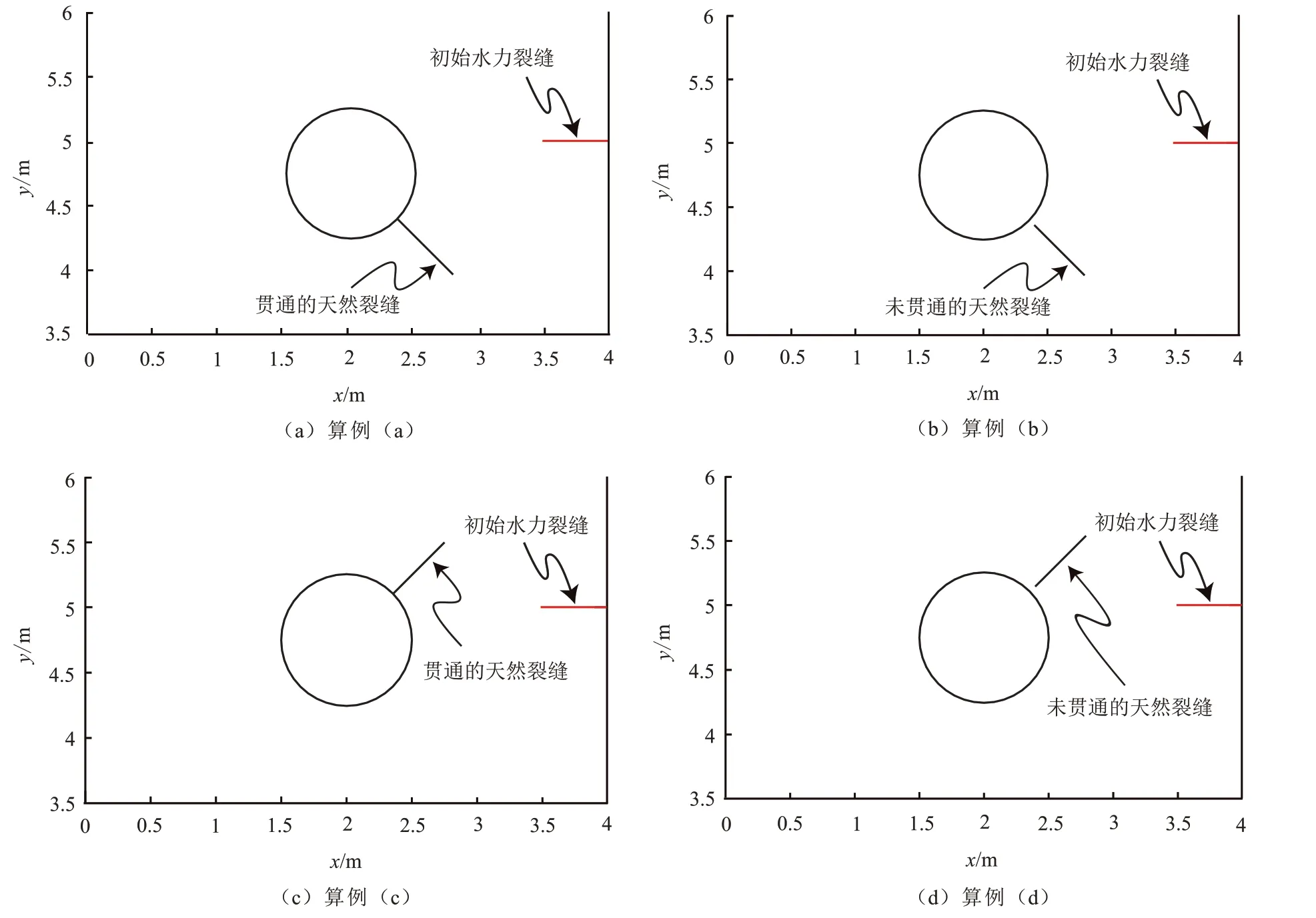
图11 孔洞附近天然裂缝影响算例示意Fig.11 Simulation case sketches of effect of natural fracture around cavity
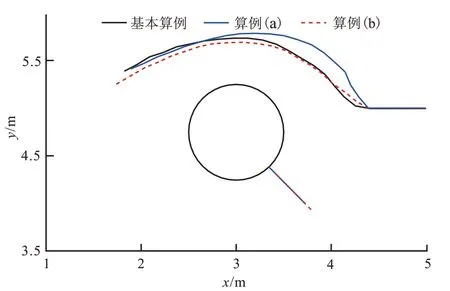
图12 天然裂缝对扩展路径的影响:算例(a)及算例(b)Fig.12 Effects of natural fracture on fracture propagation paths:Case(a)and Case(b)
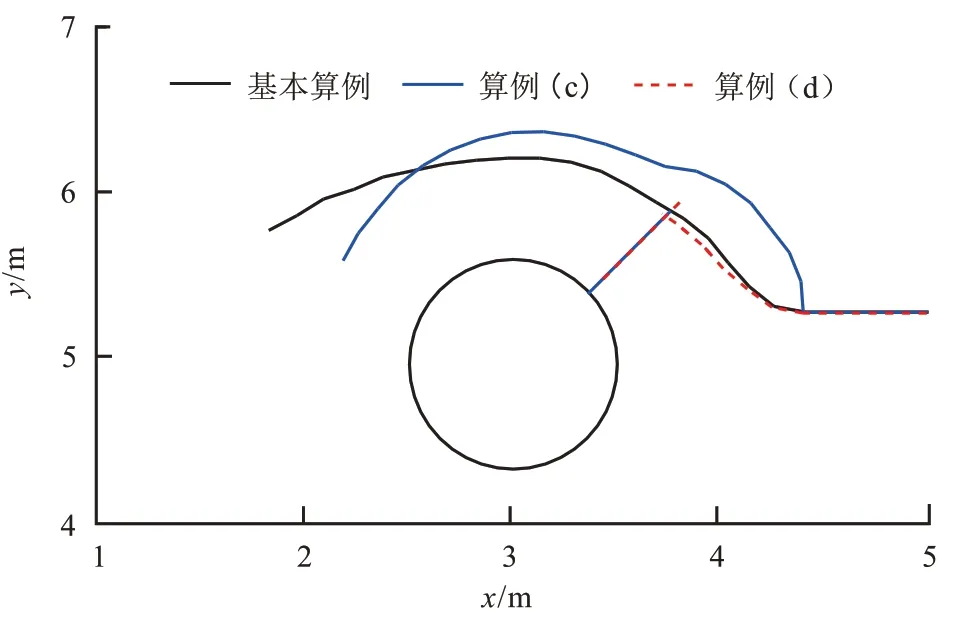
图13 天然裂缝对扩展路径的影响:算例(c)及算例(d)Fig.13 Effects of natural fracture on fracture propagation paths:Case(c)and Case(d)
3.2 顺序压裂仿真
研究位于两相邻压裂段(裂缝1、裂缝2)之间的孔洞对裂缝扩展行为的影响。模型尺寸为100 m×100 m,裂缝间距为10 m,初始裂缝长度为2.5 m,孔洞半径为2.0 m,孔洞相对于井筒的高度为3 m。水平方向和竖直方向地应力分别为20 MPa和30 MPa。储层材料参数E=28 GPa,ν=0.2,KIC=1.0 MPa·m1/2。压裂液黏度μ以及泵注排量Qinj分别为10 mPa·s、0.001 m3/s,压裂液滤失系数CL取值为10−5m/s1/2,泵入的支撑剂体积分数为0.3。依据笔者先前的研究[7],利用有限差分方法计算支撑剂体积浓度分布情况c,然后借助wp=woc/η即可求得支撑裂缝宽度(其中wo表示压裂完毕后返排前的裂缝宽度,η为支撑剂铺置密度系数,取值为0.74),最后利用罚函数法[7]模拟支撑裂缝。模型总共划分10 281 个四边形单元,裂缝扩展步长为0.85 m。
计算获得裂缝扩展路径如图14 所示,其中虚线和实线分别表示无孔洞和有孔洞2 种情形。从图14 中可以看到,位于两条相邻水力裂缝之间的孔洞会对其附近裂缝的扩展轨迹产生显著影响。无孔洞时,裂缝1 沿着直线扩展,裂缝2 受到支撑剂支撑裂缝1 的应力阴影效应影响,朝着远离裂缝1的方向发生偏转,最终形成关于井筒对称的扩展路径。存在孔洞时,受到孔洞应力场的影响,裂缝1 上下两端均朝向左侧偏转,且井筒下侧(y小于0)偏转程度稍高于上侧(y大于0);对于裂缝2,井筒上方的裂缝(y大于0)远离孔洞扩展,井筒下方的裂缝(y小于0)首先朝右扩展,然后再向左扩展。
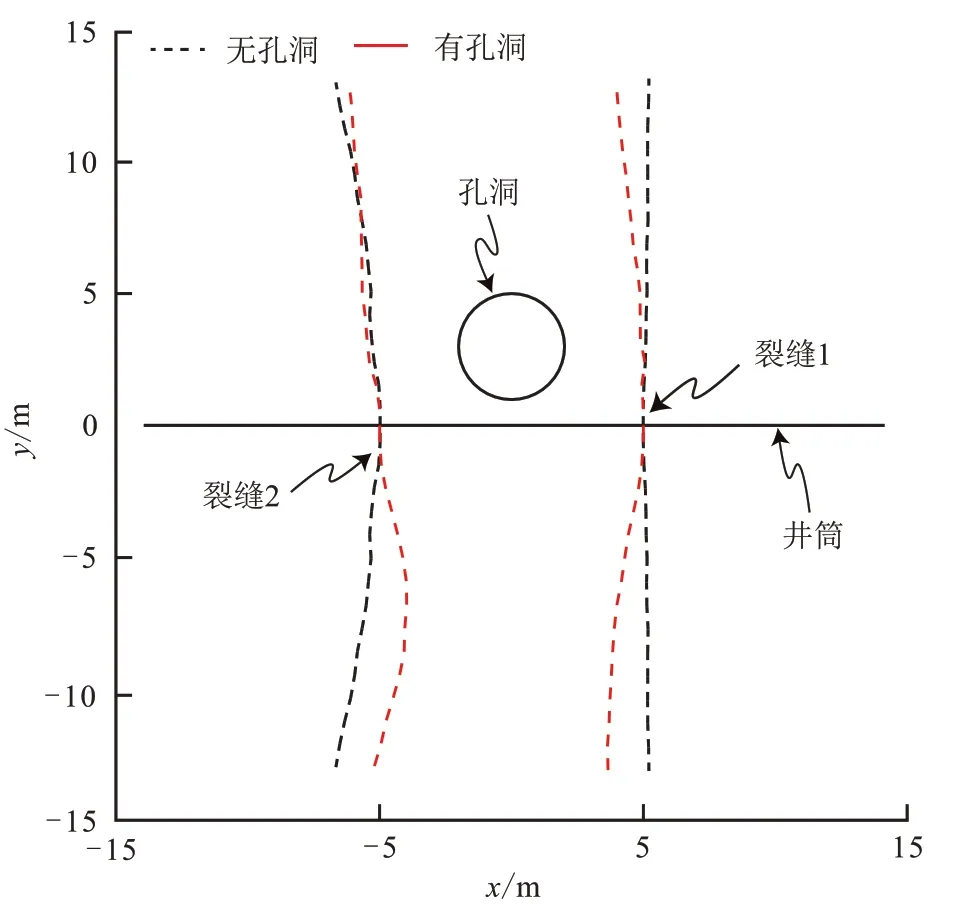
图14 无孔洞和有孔洞时的裂缝扩展路径对比Fig.14 Comparison of propagation paths of cases with and without cavity
4 结 论
(1)地应力水平和侧压力系数(或地应力差)都会对孔洞附近水力裂缝的扩展路径产生较大影响。提高侧压力系数会增强孔洞的影响,从而使得裂缝扩展路径弯曲程度增加;较低的地应力水平或较小的地应力差可以减弱孔洞的影响,有利于水力裂缝朝着孔洞方向扩展。
(2)考虑孔洞的情况下,压裂液黏度和泵注排量是压裂设计过程中影响裂缝扩展路径的2 个关键参数,提高压裂液黏度和排量都能够减弱孔洞对水力裂缝的影响,有利于水力裂缝沿其原有方向扩展。
(3)未与孔洞贯通的天然裂缝对孔洞周围应力场的影响较为有限,而与孔洞贯通相连的天然裂缝由于可以发生摩擦滑动,因此会进一步增强孔洞周围的应力集中效应,最终水力裂缝偏转程度更高,不利于形成复杂压裂网络。
(4)与没有孔洞的情况相比,存在于2 个相邻压裂裂缝之间的孔洞会显著改变其周围应力场,造成不规则的压裂裂缝扩展路径。
