演化博弈理论下社保基金给付环节的监管分析
2022-08-08宋成志
宋成志
(长春大学 经济学院,吉林 长春 130022)
随着我国社会保险基金总体规模的不断扩大,有关社会保险基金给付环节的问题也愈发凸显。2012年由国家审计署发布的第34号文件《全国社会保障资金审计结果》就曾指出一些地方机构和单位工作人员在社会保障资金的给付环节存在违规违纪问题,如由于一些机构审核较为宽松,使共18.52亿元被发放给无资格人员用于待遇或报销费用,涉及不规范发放社会保险待遇或报销费用范围达21个省、165个市和748个县,涉及不规范发放最低生活保障待遇范围达8个省、178个市和1 899个县等等,违规范围之广令人深思。截至2021年底我国社会保险基金规模达到了94 378.7亿元,应加强给付环节的审核监管,保障资金安全。当下,我国社会保险基金给付环节的监管以对经办机构和发放机构以及参保企业或参保人的行为监管为主,其中,对参保企业或参保人的行为监管主要是依法审查领取人员是否符合享受条件和有无骗取保险金行为。基于以上内容,本文对社会保险基金给付环节领取者与监管者的行为选择问题进行演化博弈分析。
一、社会保险基金给付环节的问题
(一)冒领成本低
在社会保险基金的实际管理过程中,一些管理机构没有把防冒领当成工作重点,导致冒领社会保险基金较简单。我国的法律规定社会保险经办机构发现保障金被冒领时,立刻停止保障金的发放,并对已经发放的要求追回,拒不退回的处以500元以上1 000元以下的罚款。[1]但在实际操作的过程中,即使有人冒领,社会保险经办机构与执法人员在看到一些家庭特别困难时往往难以依照法规落实,甚至从人道主义出发,不予追究,[2]从而使冒领社会保险金风险成本较低。
(二)监管成本高
当前,社会保险经办机构委托银行等发放社会保障金,这使得用人单位只负责缴纳,不再管理退休人员的社会保障金。相关部门因城市大规模改造或者人口迁移,导致退休人员的信息无法及时更新,从而使得领取者在冒领之后,无法及时调查取证。[3]为防止冒领行为的产生,一些省份要求退休人员在规定时间、地点接受常规检查,但这些检查需要耗费大量的人力、物力,致使监管成本高,效率低,不利于社会保险基金给付环节的监督。[4]
二、静态演化博弈分析
(一)假设条件
本文的博弈模型将社会保险基金领取者抽象为一个市场主体,他在与监管者博弈的过程中,由于主体的有限理性以及信息不对称,双方在进行策略决断时无法判断自己的选择是否达到自身利益的最大化。[5]领取者在不监管的情况下易做出提供虚假资料来冒领的道德缺失行为,甚至有可能在监管者进行监管的时候选择冒领。但也有可能领取者诚实守信,不管监管者是否监管都选择不冒领。[6]监管者也会有两种决策行为,一个是进行监管,一个是不进行监管。双方的博弈策略组合矩阵如表1所示。

表1 博弈策略组合矩阵
(二)构建博弈模型
博弈参与者的每一种策略都有其不同的成本收益,对于领取者来说,当领取者选择不冒领策略时,没有额外收益,即收益为0。当领取者选择冒领策略即违法领取社会保险金,而监管者没有认真监管,无法发现领取者的违法冒领行为时,那么领取者获得额外收益E。对于给付环节的监管者而言,当其选择监管策略时,会获得社会总收益G,监管成本是C。监管者发现领取者冒领,罚没额外收益E外,还会对其进行处罚,罚金为P。当其选择不监管策略时,会因为领取者冒领造成声誉损失L,具体假设参数如表2所示。

表2 参数假设
在监管者进行监管的前提下,假设领取者冒领就会被监管者发现并且加以处罚,领取者不冒领的成本收益为0,监管者的成本收益为G-C;领取者冒领的成本收益为-P,监管者的成本收益为G-C+P。
在监管者不进行监管的前提下,领取者不冒领的成本收益与监管者的成本收益均为0;领取者冒领的成本收益为E,监管者的成本收益为-L。双方的博弈成本收益组合矩阵如表3所示。

表3 博弈成本收益组合矩阵
在此基础上,分析监管者与领取者的最优博弈策略,假设监管者在采取监管策略的情况下,令领取者以y的概率采取不冒领策略,以1-y的概率采取冒领策略,那么监管者对应的收益函数表达式为:
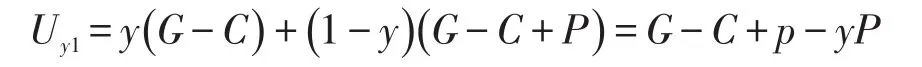
当监管者采取不监管策略的情况下,领取者还是采取上述概率策略,由此监管者对应的收益函数表达式为:

由Uy1=Uy2,得y=(G-C+P+L)/(P+L),监管者在该监管概率下,不管是采取监管还是不监管策略,监管者的收益都是一样的,该概率是监管者监管策略的纳什均衡。当y>(G-C+P+L)/(P+L)时,Uy1
由监管者监管策略的纳什均衡点y=(G-C+P+L)/(P+L)=(G-C)/(P+L)+1可以看出:G-C<0且监管者的收入减去成本的差与领取者不冒领的概率成正比,即监管带来的社会总收益与成本的差值越大,领取者不冒领的概率越高,同时监管者发现领取者冒领的处罚资金P及社会损失L都与领取者不冒领的概率成正比,即处罚资金越大,社会损失越大,不冒领的概率越高。
接下来探究当领取者采取不冒领策略的情况,假设监管者以X的概率采取监管策略,以1-X的概率采取不监管策略,那么领取者对应的收益函数表达式为:
UX1=0
同理,在领取者采取冒领策略的情况下,如果监管者继续采取上述概率策略,那么领取者对应的收益函数表达式为:
UX2=x(-p)+(1-x)E=-x(P+E)+E
由Ux1=Ux2得,x=E/(P+E),领取者在该点处不论选择不冒领策略还是冒领策略,其收益都是一样的,该点可以称作是领取者策略的纳什均衡点。当x>E/(P+E)时,Ux1>Ux2,此时,领取者会选择不冒领策略;当x
可以看出,领取者冒领的额外收益E与监管与否的概率成正比例关系,这表明如果领取者冒领的额外收益越大,相应的监管概率也将随之提高。另外,监管概率与罚金P成反比,即领取者冒领罚金越高,则冒领的概率越小,监管的必要性就越小。
三、动态演化博弈分析
领取者与监管者都具有明显的有限理性特征,所以领取者与监管者都需要彼此之间相互试探、相互学习与相互模仿,在不断的演化博弈中才能达到最佳的策略。在此基础上我们假设监管者的平均收益用Uy来表示,其表达式为
Uy=xUy1+(1-x)Uy2
我们假设领取者的平均收益用Ux来表示,其表达式为
Ux=yUx1+(1-y)Ux2
在此基础上,分别构建监管者和领取者各自的行为复制演化方程。监管者的行为复制演化方程如下:

dx/dt代表监管者实施监管的概率随时间变化的速度。
领取者的行为复制演化方程如下:
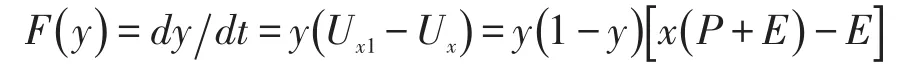
dy/dt代表领取者选择不冒领的概率随时间变化的速度。
(一)博弈的稳定性分析
由于当dx/dt=0时,实施监管的概率不再变化,这时有三个均衡状态,即x=0、x=1和y=(G-C+P+L)/(P+L);当dy/dt=0时,领取者选择不冒领的概率不再随时间变化,此时也有三个均衡状态,即y=0、y=1和x=E/(P+E)。我们根据策略稳定定理可以知道,一个稳定状态必须对微小扰动具有稳健性才能称为演化稳定策略。
1.监管者的演化稳定策略均衡
对于监管者的行为复制演化方程如下:
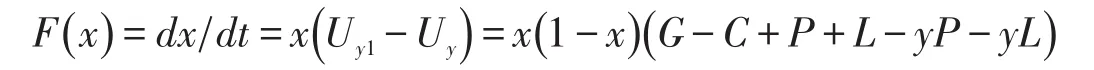
若y=(G-C+P+L)/(P+L),则F(x)=0,这表明领取者在此概率下不冒领,所有的点都是平衡点。
若y≠(G-C+P+L)/(P+L),F(x)=0时,有两个均衡点x=0、x=1,接下来探究x=0、x=1是否为演化稳定均衡,在(G-C+P+L)/(P+L)>1情况下,y一定小于(G-C+P+L)/(P+L),x取值0
根据以上结论,监管者的概率演化动态相位图如图1、图2、图3:
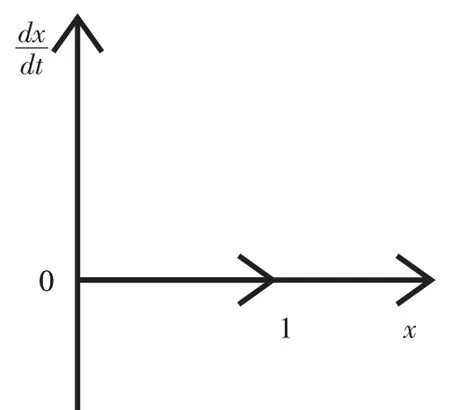
图1 y=(G-C+P+L)/(P+L)

图2 y>(G-C+P+L)/(P+L)

图3 y<(G-C+P+L)/(P+L)
2.领取者的演化稳定策略均衡
对于领取者的行为复制演化方程如下:
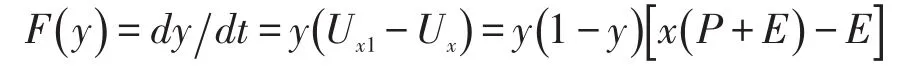
若x=E/(P+E),则F(y)=0,这表明监管者在此概率下进行监管,所有的点都是平衡点。
若x≠E/(P+E),F(y)=0时,有y=0、y=1这两个均衡点,但这两点也不一定是演化稳定均衡,在E/(P+E)>1的前提下,x一定小于E/(P+E),因此x(P+E)-E<0,因为0
根据以上结论,领取者的概率演化动态相位图如图4、图5、图6:

图4 x=E/(P+E)

图5 x 图6 x>E/(P+E) 在0<(G-C+P+L)/(P+L)的情况下,当y<(G-C+P+L)/(P+L)时,监管者演化策略为监管,即x=1;当y>(G-C+P+L)/(P+L)时,监管者的演化策略为不监管,即x=0。 在0 上述两种情况的博弈情形如图7: 图7 演化博弈路径 当0 当x 当x>E/(P+E),y<(G-C+P+L)/(P+L)时,dy/dt>0、dxdt>0,y趋向于(G-C+P+L)/(P+L)点,x趋向于1点,B不是双方演化均衡点。此时监管者倾向于增加监管,领取者倾向于不冒领,即当领取者不冒领概率低于(G-C+P+L)/(P+L)时,监管者监管概率超过E/(P+E)时,监管者倾向于提升监管。 当x 当x>E/(P+E),y>(G-C+P+L)/(P+L)时,dy/dt>0、dxdt<0。y将向1点演化,x将向E/(P+E)点演化,B不是双方演化均衡点。此时监管者倾向于提升监管,领取者倾向于不冒领,也可以理解为当领取者不冒领概率高于(G-C+P+L)/(P+L)时,监管者监管概率高于E/(P+E),监管机构倾向于监管。 通过以上分析说明,该均衡点是一种不稳定策略。 通过以上的演化博弈分析可知,在社会保险基金给付环节,双方处在一个动态平衡状态之中,领取者采取怎样的策略需要考虑其被惩罚力度和额外收益,监管者采取怎样的策略需要考虑监管成本、收益和社会损失。基于以上结论我们得出有利于社会保险基金给付环节监管的策略,希望能够保障资金的安全,推动中国经济的发展。[7] 第一,相关部门应完善相关法律法规建设,建立起完备的社会保障体系,提高违法成本,加大冒领等违规惩罚力度。由于我国相关法律体系不甚完善,再加上违法成本较低,以至违法人员铤而走险,走上违法的道路,对我国社会产生恶劣影响,应严厉打击违法犯罪行为,绝不姑息。当惩罚力度远远大于获得的收益时,才会对违法者起到警示作用。 第二,控制监管成本,提高监管效率,建立多部门信息共享平台和面部或指纹信息识别系统。在建立初期,监管成本较高,但当社会监管体系搭建起来,各部门信息联动,不再有复杂的流程。有效的信息识别系统能够快速地将领取人信息上传到信息共享平台,当有人利用虚假信息骗取保障金时,经办机构能第一时间审查到该人是否有资格领取。社会保险经办机构因相关信息掌握不足让违法者有机可乘,而建立面部或指纹信息识别系统和多部门参保人员信息共享平台,不仅能避免领取者的冒领行为,还能提高效率,降低监管成本。
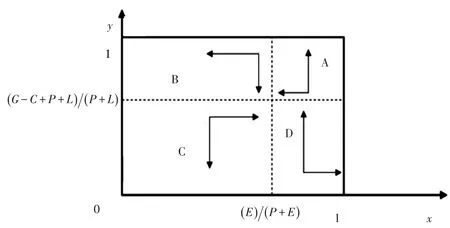
(二)演化博弈结果分析
四、结论及对策建议
