含双平行四边形结构支链的SCARA并联机构研究
2022-08-08张赵建畅博彦
梁 栋 张赵建 畅博彦 李 林 齐 杨
(1.天津工业大学机械工程学院, 天津 300387; 2.天津市现代机电装备技术重点实验室, 天津 300387;3.天津职业技术师范大学机械工程学院, 天津 300222)
0 引言
作为一类重要的工业机器人,并联机器人具有空间多闭环结构,可通过多条支链的协同作用实现动平台(末端执行器)的运动输出,其中可实现SCARA运动(三平一转,3T1R)的并联机器人快速崛起,因其具有速度快、精度高以及动态响应快等优点,在实现抓取、移动、放置等高速操作且运动灵活的工作中有独特优势,广泛应用在电子制造、食品生产、医疗卫生以及农业等领域[1-2]。
SCARA并联机构的研究一直是国内外关注的焦点。CLAVEL[3]发明了具有空间三维移动能力的Delta机构,之后以其为基础,通过在末端执行器上添加一个独立的转动输出,进而实现了SCARA运动。随着机构综合理论的不断发展,H4、I4[4-5]等具有多个动平台的并联机构相继被发明出来。黄田等[6]在H4、I4的基础上提出了具有SCARA 运动的Cross-Ⅳ型高速搬运机器人。文献[7-10]提出了X4型并联机构,其为一种单动平台的全对称SCARA运动并联机构,为后来单动平台SCARA并联机构的设计和发展奠定了基础。沈惠平等[11-13]基于机构结构降耦原理与方位特征(POC)集理论,设计了低耦合度、零耦合度且部分解耦的能实现SCARA运动的并联机构。这些机构的运动学、动力学分析相对简单,运动控制与轨迹规划较容易,所以在某些应用中有较大优势。杨廷力等[14]提出了基于单开链的构型综合方法及方位特征输出矩阵,据此综合出了一系列SCARA并联机构。
传统SCARA并联机构由于支链不含或含有较少的闭环子结构,且采用轻量化设计,其刚度、承载力等较低,故在高速/高加速度及重载运动场合下,弹性变形较大,会进一步影响末端执行器的跟踪/定位精度。针对现有机构在高速拾取、搬运、放置等作业场合下的不足,本文提出一种含双平行四边形结构支链的新型SCARA并联机构(具有工作空间大、刚度和承载力高等特点),并对此机构的拓扑结构、运动学以及运动性能进行系统性分析。
1 拓扑结构分析
1.1 机构描述
机构的三维虚拟样机模型如图1所示。

图1 机构虚拟样机模型Fig.1 Virtual proptotype model of mechanism1.静平台 2.驱动装置固定架 3.驱动装置 4.从动臂 5.主动臂 6.连接架 7.上短杆 8.杆端连接头 9.细杆 10.下短杆 11.动平台 12.末端执行器
该机构包括静、动平台以及4条相同的支链(PaRPaR),每条支链均含有2个平行四边形结构,刚度较高,可有效抵抗弹性变形。4条支链彼此相隔90°均匀地连接在静平台上,动平台采用单动平台的结构,且设计为矩形。驱动装置固定在静平台上。上下两个平行四杆机构由连接架连接,连接架与下平行四杆机构通过一轴线竖直布置的转动副连接。连接架的底面与地面始终保持水平。下平行四杆机构的末端通过转动副连接于动平台。
1.2 自由度分析
1.2.1李群理论
刚体在空间的六维运动{D}称为一个李群,即位移群。刚体在空间中的各种运动都是位移群{D}的子集。表1为利用典型位移子群表示刚体在空间内的运动[15-18]。

表1 典型位移子群Tab.1 Several displacement subgroups
1.2.2自由度
图2为该机构的机构简图。图中Ai表示第i条支链与静平台的铰链中心 (i=1, 2, 3, 4),Bi表示上平行四杆机构的主动臂与连接架的铰链中心,Ci表示下平行四杆机构的短杆中心,Di表示下平行四杆机构的短杆中心。αi表示4个主动臂转角,即主动臂与水平方向的夹角。ξ表示上四杆机构的末端和下四杆机构的上端的连线与水平方向的夹角。
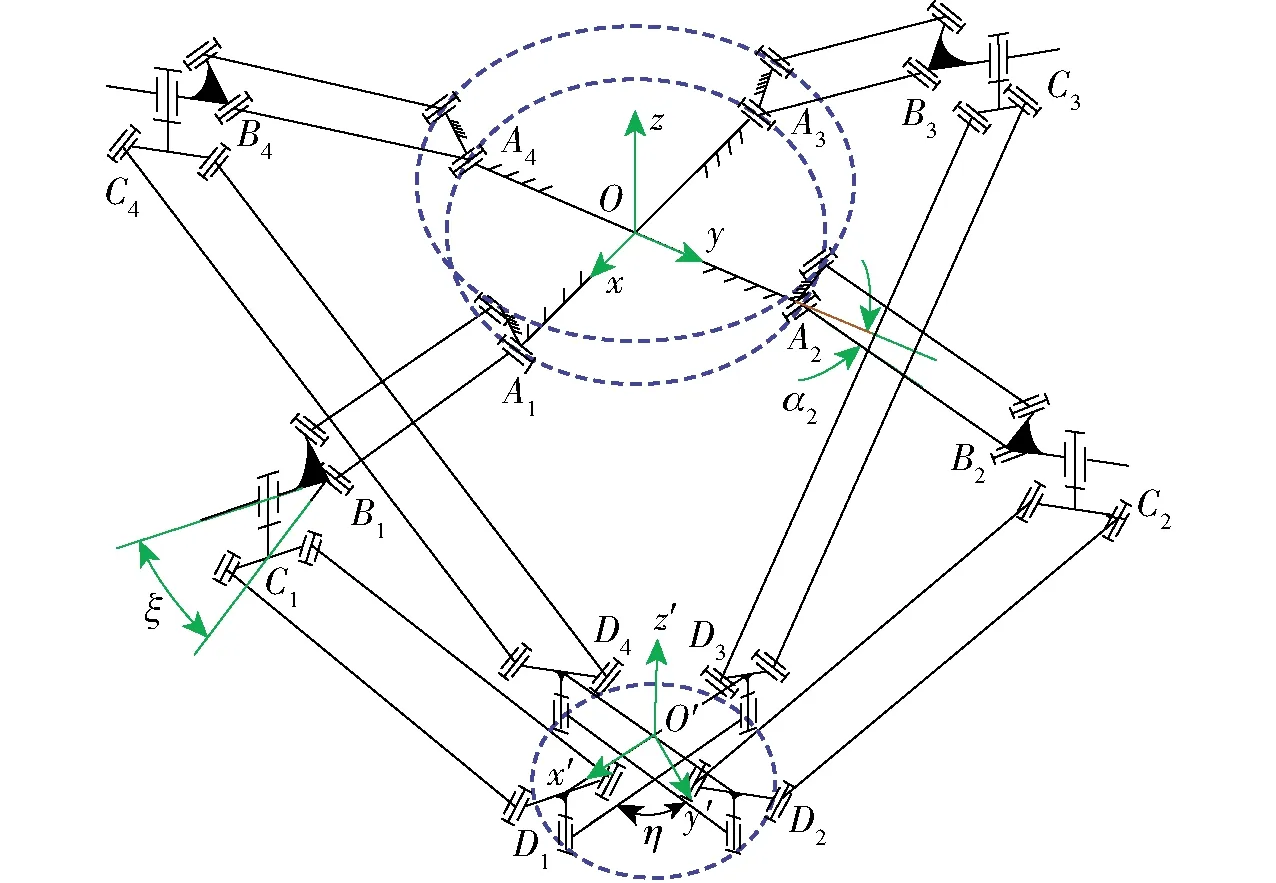
图2 机构简图Fig.2 Schematic of mechanism
在计算含闭环子链的机构自由度时,首先把闭环子链视为一个多自由度的广义运动副,然后通过约束分析,把闭环子链等效转换为几个单自由度运动副组合成的串联链,可将原来的复杂机构变成等自由度的不再含有闭环子链的并联机构,即可按照一般的自由度分析求解[16]。该机构两个复杂铰链均为4R平行四边形机构,通过上述提到的约束分析方法,可以得到这2个平行四杆机构分别等效为一个移动副。令u、v、w(分别平行于x、y、z轴)表示转动副的轴线矢量,将每条支链从上往下分为上平行四杆、连接架、下平行四杆以及动平台4部分。{Li,j}表示各支链中各部分的运动集合,i=1, 2, 3, 4,表示4条支链;j=1, 2, 3, 4,表示从上到下的4部分。
支链的上部分平行四杆机构的运动集合{Li,1}可表示为
{Li,1}={Ta(ni,1)}
(1)
式中 {Ta(ni,1)}——方向为ni,1的移动副,ni,1的方向为AiBi与Ai处转动副轴线矢量叉乘之后的方向,为一维圆弧运动
连接架与下平行四边形机构之间的转动副{Li,2}可表示为
{Li,2}={R(Ci,w)}
(2)
式中 {R(Ci,w)}——转动轴线矢量为w且过点Ci的转动副
下部平行四边形的运动集合{Li,3}可表示为
{Li,3}={Tb(ni,2)}
(3)
式中 {Tb(ni,2)}——方向为ni,2的移动副,ni,2的方向为下平行四杆的长杆所在的方向矢量与转动轴线矢量叉乘之后的方向,为一维圆弧运动
动平台与下平行四边形连接关节处的转动副{Li,4}可表示为
{Li,4}={R(Di,w)}
(4)
式中 {R(Di,w)}——转动轴线矢量为w且过点Di的转动副
则整条支链的运动集合可表达为
{Li}={Li,1}{Li,2}{Li,3}{Li,4}=
{Ta(ni,1)}{R(Ci,w)}{Tb(ni,2)}{R(Di,w)}=
{Ta(ni,1)}{Tb(ni,2)}{G2(w)}={X(w)}
(5)
式中 {G2(w)}——二维平面运动,为{G(w)}的二维子流形
{G(w)}表示法线为w的平面运动,包括平面二维移动和绕法线w的一维转动。∃s使得{T(s)}·{G2(w)}={G(w)}。
机器人动平台的自由度是4条支链末端所允许的刚体运动集合的交集,所以动平台运动集合{M}为
{M}={L1}∩{L2}∩{L3}∩{L4}={X(w)}
(6)
综上所述,该机构动平台具有4个自由度,即在空间中的三维移动和绕z轴的转动。
2 位置分析
2.1 位置正解
位置正解是已知主动臂的转角求解末端动平台位姿[19-20]。建立如图2所示的固定参考坐标系Oxyz,坐标原点O与图中静平台中心重合,静平台中心到A1的方向为x轴方向,静平台中心到点A2的方向为y轴方向,z轴方向满足右手螺旋定则。构建动坐标系O′x′y′z′,以D1D3与D2D4的交点为动系坐标原点O′,x′轴方向为原点O′到点D1的方向,y′轴过原点且垂直于x′轴,z′轴方向满足右手螺旋定则。采用闭环矢量法分析该机构的位置,用向量r表示末端执行器参考点O′相对于静坐标系原点O的位矢。闭环矢量示意图如图3所示。
结合图2、3,动平台参考点O′在固定坐标系中的位置矢量可表示为
r=lOAi+lAiBi+lBiCi+lCiDi+lDiO′
(7)
进一步改写为
lCiDi=r-(lOAi+lAiBi+lBiCi)+lO′D
(8)
用ai、bi、ci分别表示lOAi、lAiBi、lBiCi的单位方向矢量,βi表示Ai处的方位角,则
(9)
由式(9)可得
(10)
式中R1——静平台外接圆半径
L1——主动臂长度L2——连接架长度

d′i=(cosγi,sinγi,0)T
(11)
其中
ε1=ε3=0ε2=ε4=1
式中η——支链1、3末端的连线与支链2、4末端的连线的夹角,为钝角
εi——符号参数
动平台具有4个自由度,但只有一个旋转自由度,即绕z轴的旋转,故动坐标系相对于静坐标系的姿态旋转矩阵为
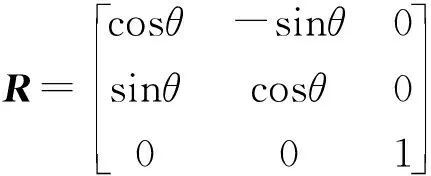
(12)
式中θ——动平台转角

(13)
其中
di=Rd′i
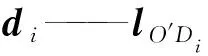
R2——动平台外接圆半径
根据杆长约束条件可得方程
‖lCiDi‖=L3(i=1, 2, 3, 4)
(14)
式中L3——从动臂长度
由式(8)~(14)得
(15)
式(15)即为该机构的位置正解模型,是以x、y、z以及θ为未知量的非线性方程组。该方程组无法求得其解析解,可借助牛顿-拉普森迭代法[21]求得其数值解(见下文数值算例)。
2.2 位置逆解
位置逆解是已知末端动平台的位姿反求主动臂转角[19-20]。将式(15)整理为
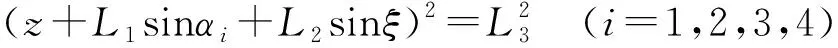
(16)
将式(16)简记为
Mi1cosαi+Mi2sinαi+Mi3=0 (i=1,2,3,4)
(17)
其中
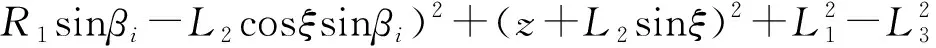
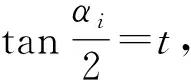
(18)
式(18)即为逆解模型,即给定末端动平台的位姿,可得4条支链的主动臂转角位移。由此可见,机构共有16组逆解,考虑到机构的实际装配,式(18)中根号前取“-”号。
2.3 位置算例验证
不失一般性,取表2中各杆件长度。借助Matlab软件进行数值仿真,验证位置正/逆解模型的正确性。

表2 机构尺寸参数Tab.2 Various dimensional parameters m
算例1:给定末端平台参考点O′的位置为x=0.2 m、y=0.1 m、z=-0.6 m、θ=π/3。通过Matlab软件编写逆解程序,可以得出α1=-0.706 9 rad、α2=-0.616 9 rad、α3=0.323 0 rad、α4=0.426 3 rad。利用牛顿-拉普森迭代法对非线性方程组式(15)进行求解。将上述逆解过程中得到的4个主动臂转角作为已知条件,用牛顿迭代法求得动平台位姿:x=0.2 m、y=0.1 m、z=-0.6 m、θ=π/3,该算例正解与逆解所得结果相互对应。再给定算例2:x=-0.3 m、y=-0.1 m、z=-0.7 m、θ=-π/4,逆解程序运行之后得到:α1=0.723 5 rad、α2=0.103 2 rad、α3=-0.658 2 rad、α4=-0.041 1 rad。将上述结果作为已知条件,代入正解方程组,运用牛顿迭代法进行求解,计算得到:x=-0.3 m、y=-0.1 m、z=-0.7 m、θ=-π/4,与算例给定条件一致。对比两个算例,正解与逆解所得结果均能够相互对应,由此可知,位置正/逆解模型推导正确。
3 速度与加速度分析
3.1 雅可比矩阵构建与速度分析
由式(7)可知,机构动平台参考点O′在固定坐标系中的位矢r=(x,y,z)T可改写为
r=lOAi+lAiBi+lBiCi+lCiDi-lDiO′
(19)
对式(19)关于时间t求导,得
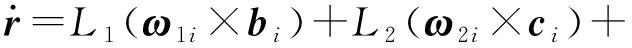
(20)
其中
(21)
式中ω1i——主动臂角速度
ω2i——连接架角速度
ω3i——从动臂角速度

wi——从动臂单位矢量
ω——动平台角速度

vi——主动臂的转动轴线,为与bi张成平面的单位法矢量

将式(21)代入式(20),得
(22)
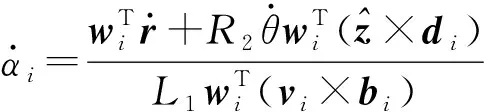
(23)
将式(23)整理成矩阵形式为
(24)
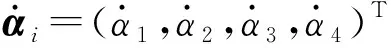
(25)
(26)
(27)
(28)
末端执行器速度与输入速度之间的关系为
(29)
式中Jq——直接雅可比矩阵
Jx——间接雅可比矩阵


J——雅可比矩阵
由式(21)、(23)可得主动臂角速度为
(30)
由式(20)、(21)可得
(31)
对式(31)两端叉乘wi,得从动臂角速度为
(32)
其中
式中wix、wiy、wiz——wi的3个分量
3.2 加速度分析
在速度分析基础上进行加速度分析,对式(20)关于时间t再求导,得
(33)
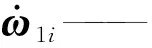
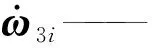


对式(21)求导,得
(34)


将式(34)代入式(33),得
(35)
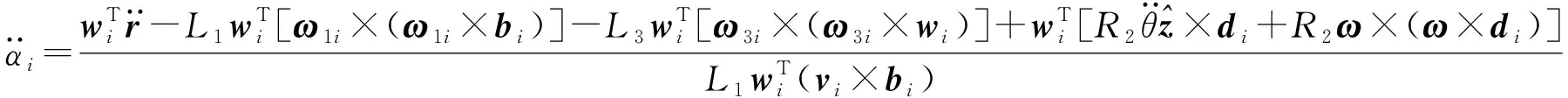
(36)
由式(32)进一步整理得到从动臂的角加速度为
(37)
3.3 角度、角速度、角加速度对比
给定仿真轨迹:规划动平台参考点O′在z=-0.8 m的平面上走一个半径为0.3 m的圆轨迹,且给定动平台转角θ为0°。基于上述分析,求得主动臂角度、角速度及角加速度的变化曲线,如图4所示。
由图4可知,给定轨迹后,所得主动臂转角、角速度以及角加速度的变化曲线平滑、连续且成导数关系,说明该机构的运动学分析准确。
4 工作空间与运动性能
4.1 工作空间
并联机构的工作空间是指在考虑各种约束条件下(杆长约束、运动副转角约束等),末端执行器的工作区域[22-24]。利用上述位置分析中的逆解,采用极限边界搜索法[23]求解工作空间。首先是一个平面上的搜索,极径ρ从零开始增大到一定值结束,符合条件的点保存,否则舍弃;极径ρ达到一定值后开始圆周搜索,搜索一周转过的角度为2π,至此完成一个平面的搜索。然后开始在z轴搜索,将z轴的范围等距离散,满足条件的保存,反之不保存。至此,工作空间内的点搜索完毕,其包络面即为工作空间。图5为极限边界搜索法流程图。
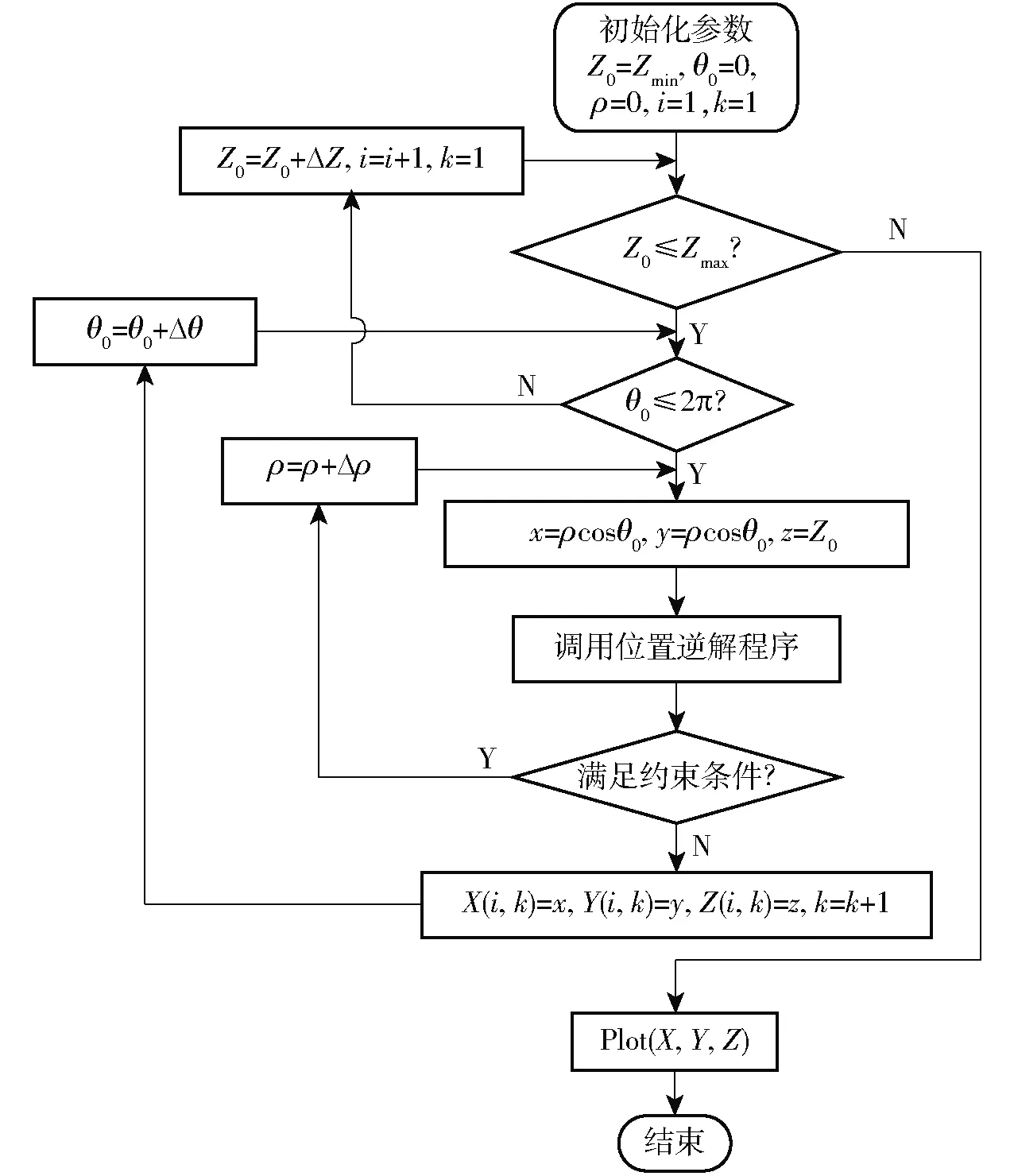
图5 极限边界搜索法流程图Fig.5 Flow chart of limit boundary search method
根据杆长及运动副转角等约束,确定搜索范围,取极径搜索范围为0≤ρ≤0.8 m,将其等距离散为150份,将圆周2π等距离散为150份,搜索动平台转角θ为0°时的定姿态工作空间,z轴循环从-1.5 m到0.5 m进行搜索,取定步长为0.01 m,为避免杆件干涉,设主动臂转角为-π/6≤αi≤π/3。利用上述方法并借助Matlab软件,工作空间求解结果如图6所示。
由图6可看出,机构在动平台转角为0°时的定姿态下,其工作空间关于中心对称,工作空间外廓光滑,体积较大且内部无空洞,说明机构在0°定姿态下的工作区域较大,机构比较合理。
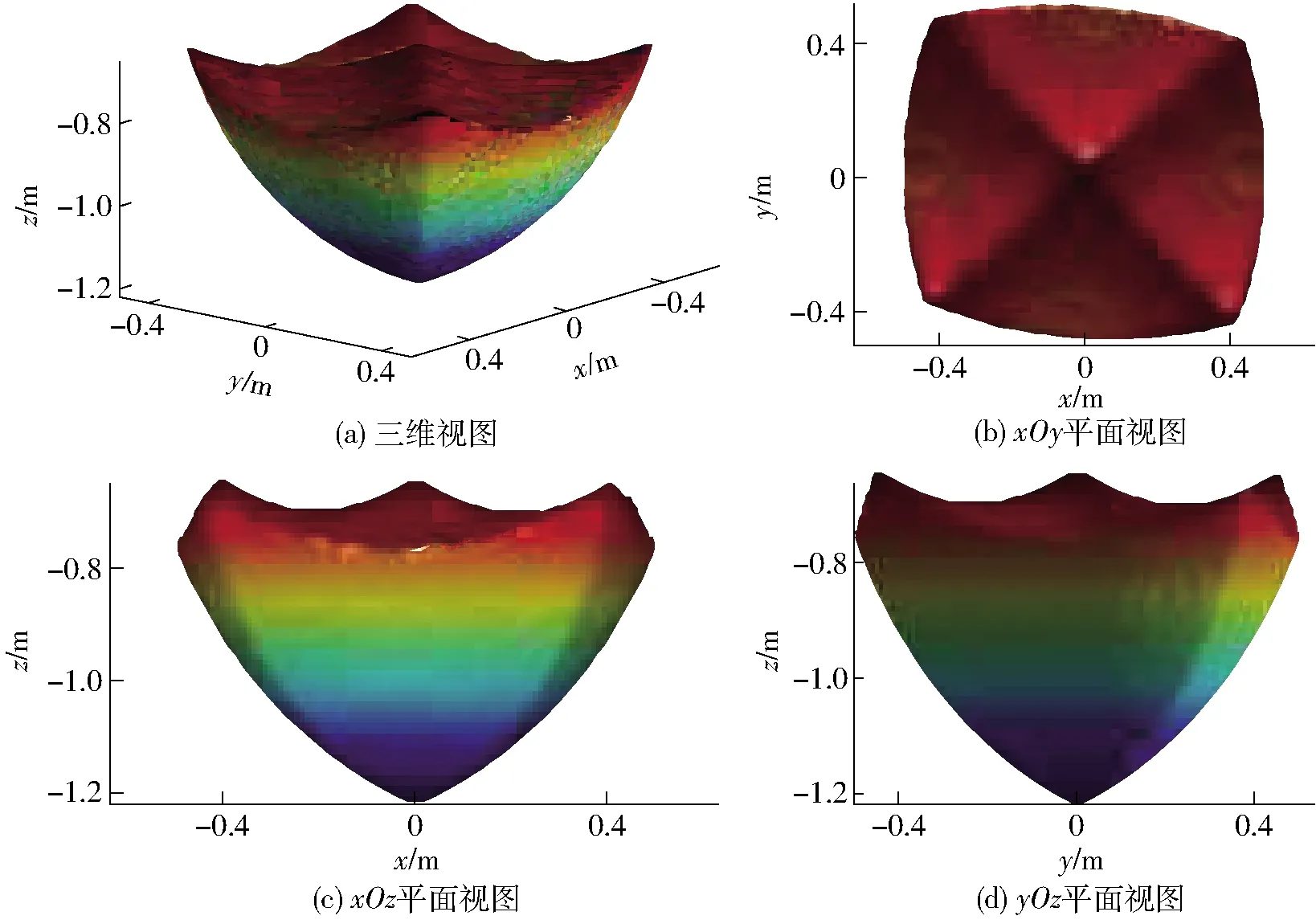
图6 转角为0°时工作空间各视图Fig.6 Various views of workspace when angle was 0°
取动平台转角为-30°,其他搜索条件不变,所得工作空间如图7所示。
由图7可知,在转角为-30°时的定姿态下,工作空间外廓依旧光滑连续,机构的工作区域较大,并关于中心对称,且相对于0°姿态下的工作空间有一定减小。
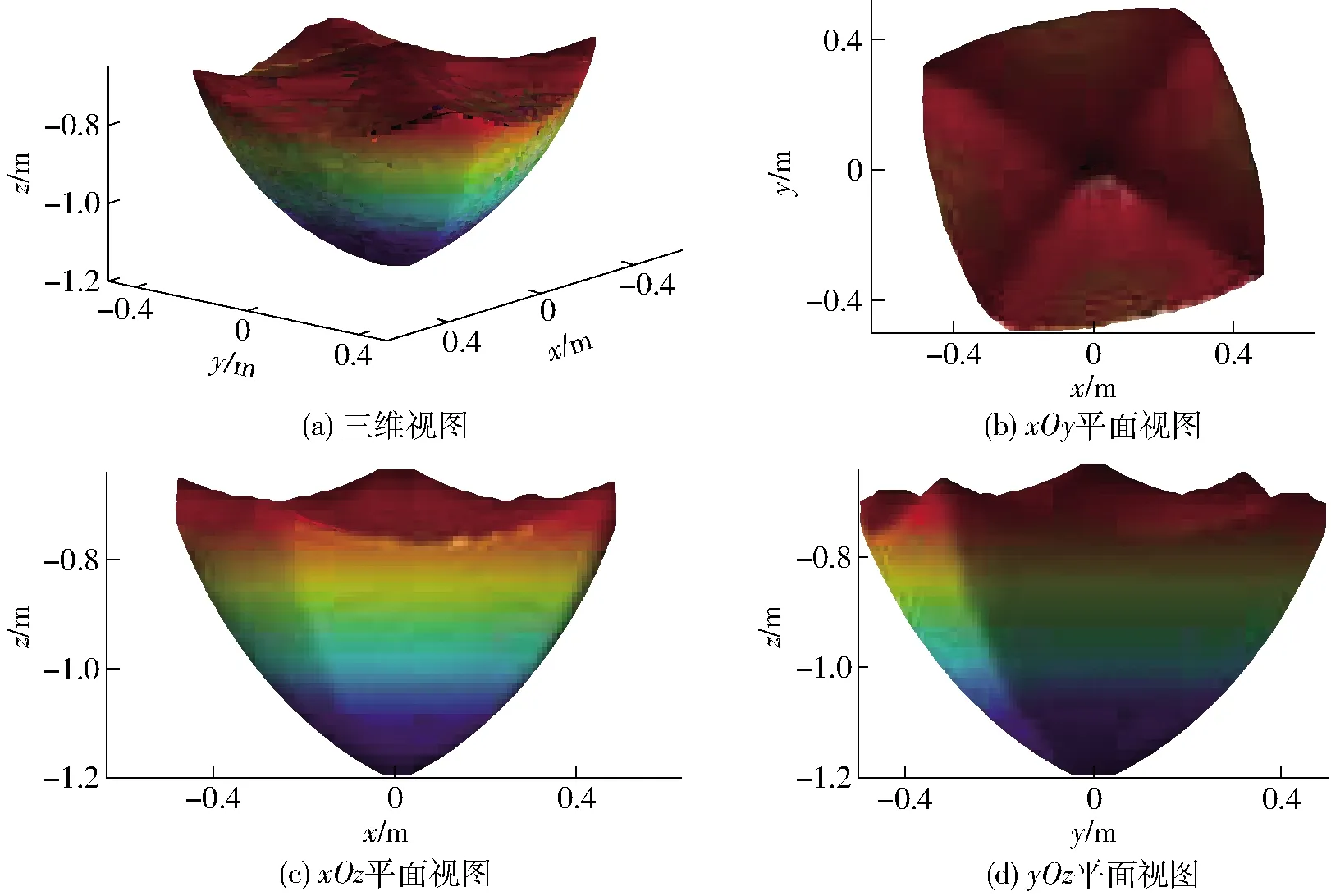
图7 转角为-30°时工作空间各视图Fig.7 Various views of workspace when angle was -30°
4.2 动平台转动能力
动平台在工作区域内的转角范围是衡量并联机构动平台转动能力的一个重要指标[24]。选择不同高度的x-y截面来分析该机构动平台的转动能力。首先在初始位置处开始转角循环,满足约束条件的记录下来,反之舍弃;然后开始下一位置处的角度循环,直到某一截面上的点(某一高度下可达工作空间内的所有点)均循环一遍之后,搜索结束。转动角度分别取最大、最小值,由此得到此截面上的最大、最小转动角度的分布情况。
取不同平面(z=-0.75 m、z=-0.9 m、z=-1.1 m),设定极坐标半径范围0≤ρ≤1 m,极坐标搜索后得到的截面为可达工作空间,分别计算动平台在此截面内的每个点的最大转角γmax和最小转角γmin,结果如图8所示。
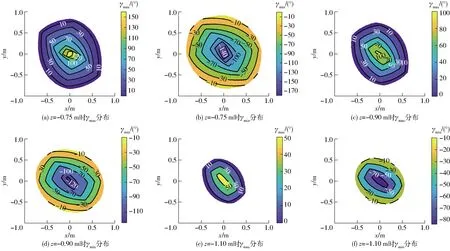
图8 不同高度下的转角γmax、γmin的分布情况Fig.8 Distribution of γmax and γmin at different heights
由图8可知,以上3个平面上的转角γmax与γmin的分布较均匀,等高线平滑,无突变。中间接近z轴处的最大转角最大,在z=-0.75 m这一平面上可达到150°左右,随着距离z轴越来越远,γmax越来越小。最小转角的分布与最大转角类似,在z=-0.75 m时,z轴附近的最小转角可达到-170°左右,向外逐渐变大。由此可知,动平台在中间的转动能力最大,随着末端动平台参考点O′距离z轴越来越远,转动能力减弱。通过以上几个平面的分析可知,该机构的转动能力较好,由内而外转动能力依次降低,符合规律。
4.3 运动性能
灵巧度是衡量机器人运动性能的重要指标[25],反映在某一位置时末端执行器获得运动传递性能。
目前灵巧度性能指标主要由可操作度与条件数两种方法来表示。条件数指标定义为[25-26]
cond(J)=‖J‖‖J-1‖
(38)
式中 ‖J‖——雅可比矩阵的Frobenius范数
根据上述所求雅可比矩阵,可知条件数与结构尺寸和位形有关系。当其趋于无穷大时,机构处于奇异位形,性能变差甚至失去运动能力。当其等于1时,机构运动传递性能最优。一般条件数在做纯移动或纯滚动的机构中应用较广泛[25]。但在含有不同类型自由度的机构中(既含有转动自由度也含有移动自由度),由于雅可比矩阵内部元素量纲不统一,会对分析结果造成偏差,不能正确反映机构的运动传递性能[18]。因此,本文利用特征长度因子[27]对雅可比矩阵进行量纲齐次化处理,即
(39)
式中Jh——齐次雅可比矩阵
Jh1——原雅可比矩阵的前3列
Jh2——原雅可比矩阵的第4列
L——特征长度因子
各向同性条件可进一步表达为
(40)
式中λ——一个非零标量
O——零矩阵
I3——3×3单位矩阵
将Jh1、Jh2相关表达式代入式(40)求解,可得
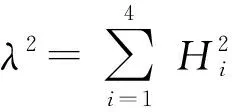
(41)
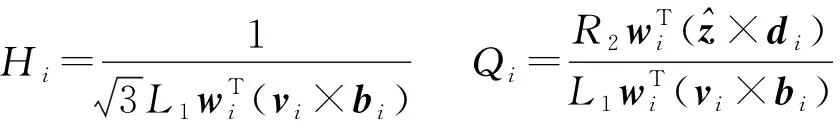
机构条件数指标表达式为
(42)
为更好地观察机构的运动传递性能,一般取条件数的倒数,即κ(Jh)=1/cond(Jh)。将工作空间中所有点的坐标值代入雅可比矩阵,结合式(42),可得到其灵巧度的空间分布。
选取末端执行器位于θ=0°时的定姿态,借助Matlab软件,得到机构的灵巧度分布如图9所示。
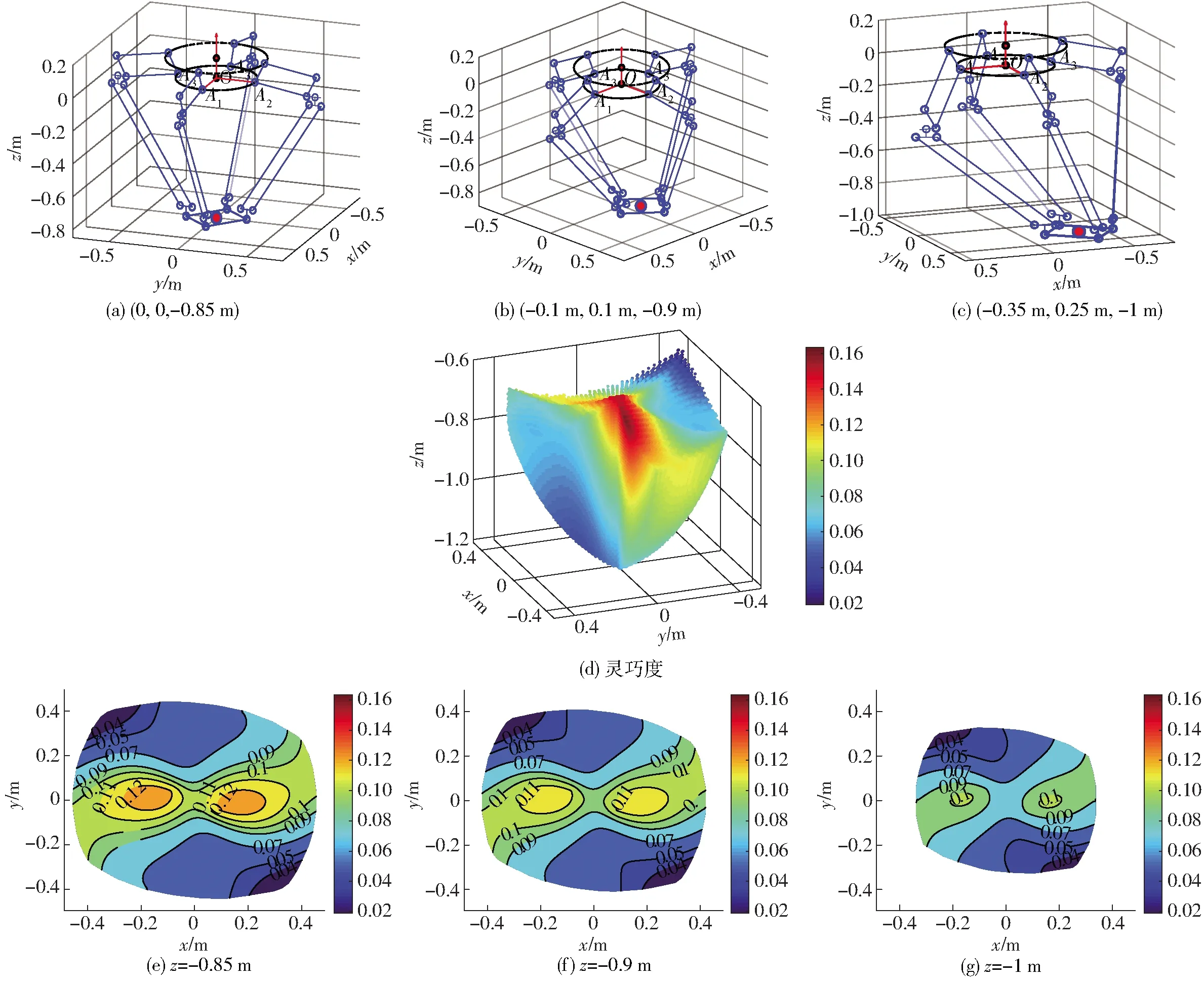
图9 灵巧度空间分布结果以及某位置下的构型图Fig.9 Condition number distributions in whole workspace and configuration diagram of certain position
由图9可知,κ(Jh)在0.02~0.16之间连续变化,无突变,表明该机构具有较好的运动传递性能。在图9d~9g所示深蓝色区域,κ(Jh)较小,运动性能略差,这是因为该机构采用矩形平台,矩形较短的边距离工作空间边界位置相对较近,所以该处κ(Jh)较小,运动性能略差。中间处κ(Jh)最大,性能最好。两个长边距离工作空间边界处相对于短边较远,所以κ(Jh)较大,在相应位置处有较好的运动传递性能。需指出,该机构在经优化设计后,运动性能可进一步提高。
基于求得的量纲齐次雅可比矩阵,定义可操作度指标为[24]
(43)
当σ=0时,末端执行器位于奇异位置,当σ≠0时,可操作度越大,机构运动性能越好。选择不同平面来分析该机构的可操作度。
选择z=-0.85 m的平面,结合式(43),得到可操作度的空间分布结果如图10所示。
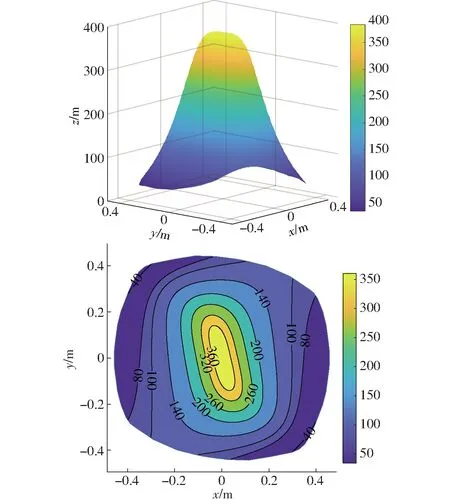
图10 θ=0°定姿态可操作度(z=-0.85 m)Fig.10 Fixed attitude maneuverability at θ=0° (z=-0.85 m)
选取z=-1 m的平面,得到可操作度的分布,结果如图11所示。
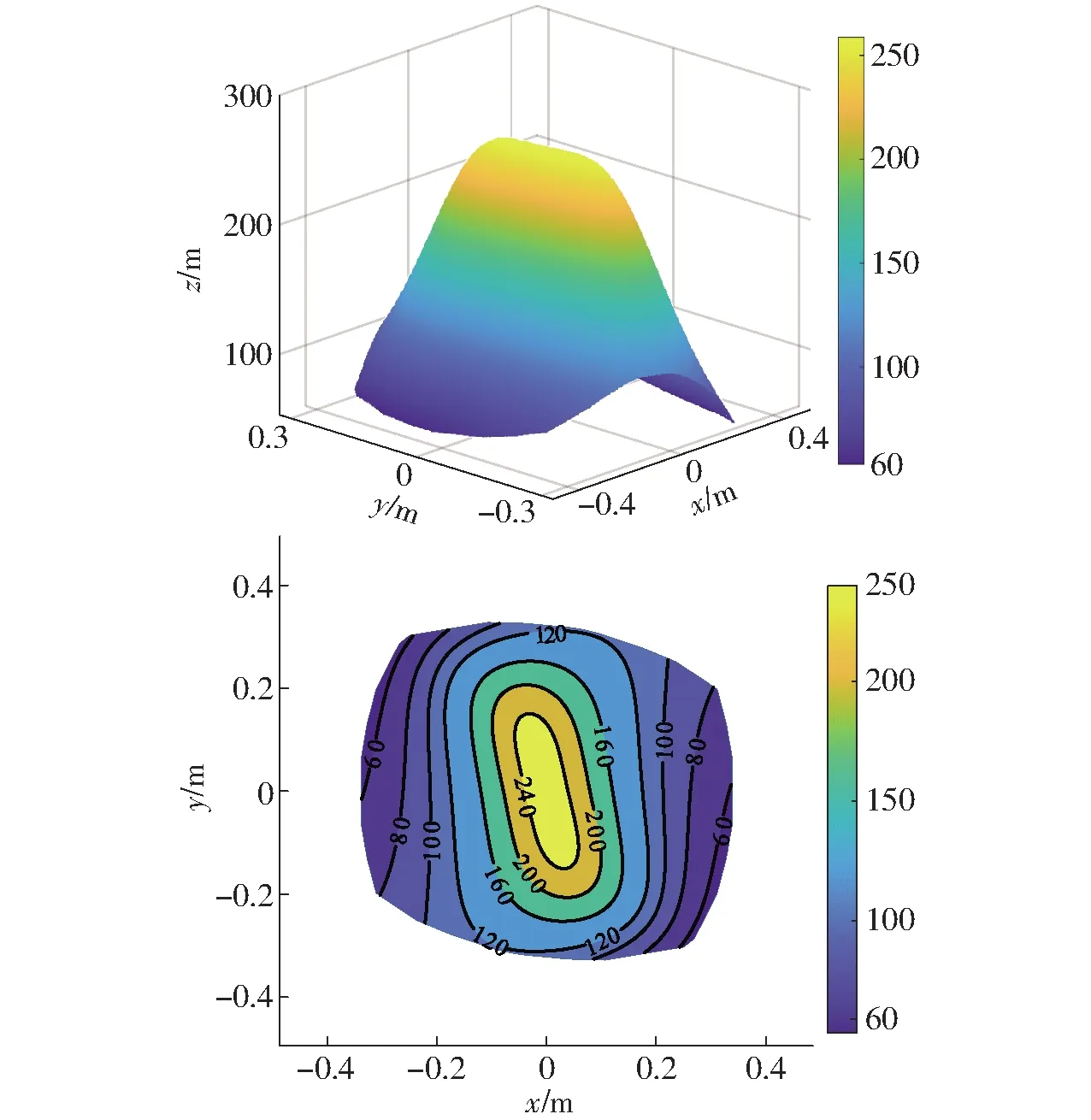
图11 θ=0°定姿态可操作度(z=-1 m)Fig.11 Fixed attitude maneuverability at θ=0° (z=-1 m)
由图10可知,σ在50~400范围内变化,其与动平台的形状、工作空间的边界处均有关系。图11中具有相似的分布情况,且σ在60~250范围内变化。可操作度结果与条件数结果大致对应,表明该机构运动传递性能较好,靠近工作空间边界处的区域,性能较低。
5 奇异性分析
当机构处于奇异位置时,运动性能大大降低,甚至失去运动能力,从而导致机构被损坏。串联机器人与并联机器人均具有奇异位置,并联机器人由于有多条支链形成的多闭环结构相互制约的特点,奇异性相对比较复杂。本文采用雅可比矩阵来分析奇异位置[11-20]。
5.1 第一类奇异
该类奇异又称边界奇异,当直接雅可比矩阵降秩时,即行列式的值为零,机构发生边界奇异[18]。结合前述雅可比矩阵可得,当det(Jq)为零时,机构中一条或多条支链处于工作空间边界位置,驱动副失去某个方向上的运动能力。记直接雅可比矩阵Jq对角元素为Jqi(i=1,2,3,4),即Jq=diag(Jqi),Jqi中一个或多个为零时,Jq发生降秩,Jqi为
(44)
式中wi——从动臂单位矢量
lAiBi——主动臂的方向矢量
由式(42)可知,当主动臂与从动臂平行时,Jqi=0,此时Jq降秩,为第一类奇异位置,也是该机构的工作空间边界点。图12给出了两种奇异位形。

图12 第一类奇异位形Fig.12 The first kind of singular configuration
结合图12可知,当产生奇异时,主动臂转角(主动臂与水平面夹角,向下为正)大于π/2,机构杆件之间易产生干涉,为防止机构杆件之间的干涉,取主动臂转角为-π/6≤αi≤π/3,在此条件下可避免第一类奇异。
5.2 第二类奇异
该类奇异又称正运动学奇异,当间接雅可比矩阵Jx降秩,即det(Jx)=0时,发生该类奇异。在第二类奇异位置处,锁定机构的驱动关节,末端动平台仍然可以产生一定的运动,即至少获得一个自由度[11]。Jx为
(45)
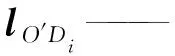
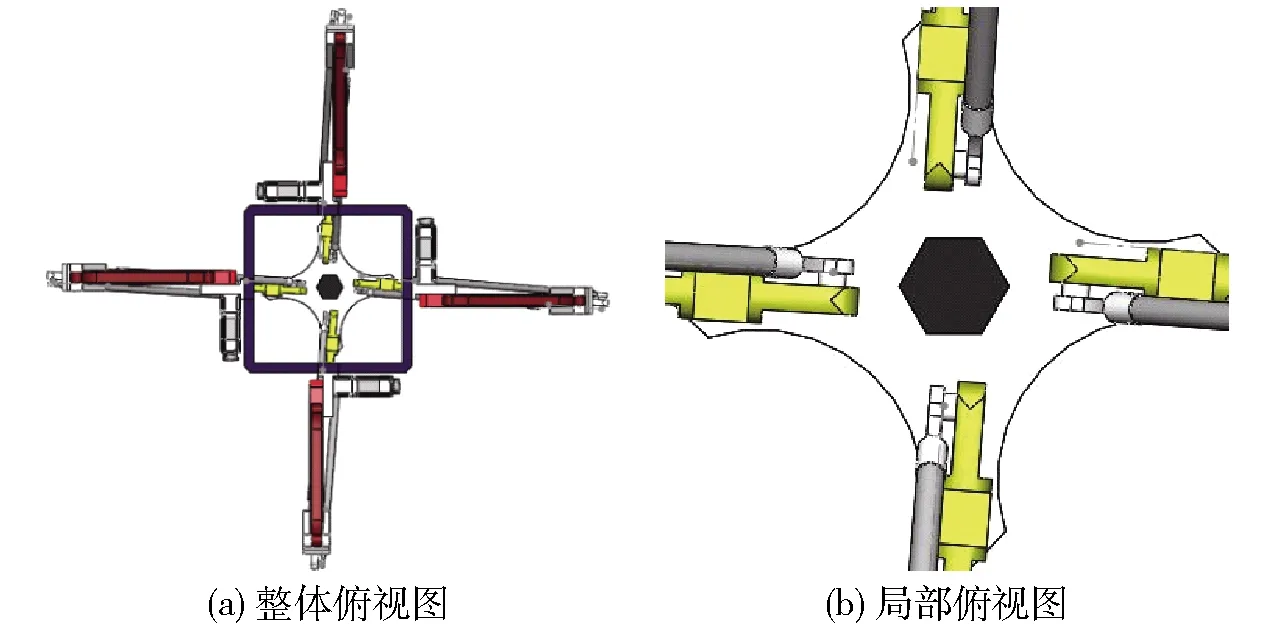
图13 第二类奇异位形Fig.13 The second kind of singular configuration
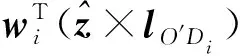
5.3 第三类奇异
该类奇异又称混合奇异,当直接雅可比与间接雅可比均降秩[11-18]时,即det(Jq)=0且det(Jx)=0时,发生该类奇异。此时末端执行器位于工作空间的边界点,驱动副失去某个方向的运动能力,而末端又仍然存在未被约束的自由度。因该机构通过设定主动臂转角范围,避免了第一类奇异,故不存在混合奇异。
6 仿真实验
为验证前述理论分析的正确性,借助ADAMS软件对该机器人机构进行仿真实验。将机器人的SolidWorks三维虚拟样机模型导入ADAMS,导入之后,对约束进行定义,并添加电机驱动。依据前述运动分析,在Matlab中规划好相应轨迹,即在1 s内走一个半径为0.3 m的圆轨迹,利用位置逆解可求得4条支链的主动臂输入转角。然后,把主动臂转角数据从Matlab导入到ADAMS中,作为驱动输入进行仿真实验。仿真过程中,机器人的运动情况如图14所示。仿真实验结果表明,机器人末端执行器能够完全跟踪期望轨迹,证明了该机构结构设计的合理性和运动分析的正确性。
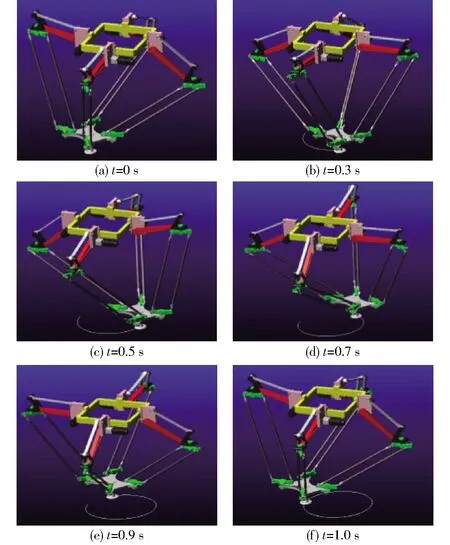
图14 ADAMS仿真实验中一个周期内末端执行器各时刻所处的位置Fig.14 Position of end effector at each time in a cycle in ADAMS simulation experiment
7 结论
(1)提出了一种可实现SCARA运动的新型并联机构,其4条支链相同,整体结构紧凑。由于支链含有双平行四边形结构,比不含闭环结构的支链具有更高的承载能力、刚度以及稳定性。
(2)基于李群理论证明了该机构有4个自由度,即3T1R。在拓扑分析基础上,借助闭环矢量法求得了位置正/逆解、雅可比矩阵、速度及加速度等,数值仿真结果正确合理,彼此之间相互对应,机构运行平稳,为后续控制策略设计奠定了基础。
(3)通过极限边界搜索法得到的机构工作空间较大,中间无空洞,外廓曲面光滑。动平台的最大、最小转动角在工作空间的分布均匀,无突变,且转动范围较大,证明机构具有较好的转动能力。利用量纲齐次雅可比矩阵分析了条件数和可操作度,两种方法得到的结果表明该机构在工作空间内的运动传递性能优良。
(4)利用直接、间接雅可比矩阵分析了该机构的几类奇异位形,可以发现,通过设置一些约束条件和动平台采用矩形形状可有效避免机构的奇异位形。在理论分析基础上,借助ADAMS多体动力学软件进行了轨迹跟踪仿真实验,进一步证实了该机构结构设计的合理性和理论分析的正确性。
