基于变种群模因算法的大规模配电网重构

孙新宇， 王 淳， 吴龙杰， 张 弛， 张 敏

（南昌大学信息工程学院，南昌 330031）

0 引 言

配电网重构是通过改变支路开关状态来改变网络拓扑从而优化系统运行性能的重要优化手段。因其无需增加额外投资，利用已有供电设施提高系统运行性能，故一直备受研究人员关注［1］。

配电网重构是一个离散、非线性的大规模组合优化问题，属于NP 难问题。随着配电网规模增大和网络结构复杂性增加，重构优化过程中产生组合爆炸现象，导致问题难以求解。大规模的配电网重构涉及到大量的拓扑分析和潮流计算，消耗大量时间，给实际应用带来困难。当前配电网重构算法［2-5］大多适用于中小规模配电网，少有方法在大规模配电网中仍具有可用性。为寻找适合求解大规模配电网重构的方法，一些学者展开了研究工作。文献［6］中提出了一种基于基本环矩阵的无不可行解编码方法，缩小了解空间的范围。文献［7］在文献［6］的基础上，提出了一种基于自适应负荷调整网络矩阵的配电网重构方法，不仅去除了解空间中的不可行解，还去除了可行解中的大量劣解，进一步精简了解空间。文献［8］中提出了一种基于图论的配电网重构方法，将配电网重构看作是在网络拓扑图中寻找最小生成树问题，利用Prim算法进行求解。文献［9］中提出了一种三段式的开关断开与交换算法，结合了支路交换法和逐次打开开关法，原理简单、性能稳定。上述方法虽然具备求解大规模配电网重构的能力，但普遍存在求解精度不高、求解时间过长的问题。文献［10］中将配电网重构模型转化为混合整数线性规划问题，应用CPLEX 规划软件进行求解，在求解精度上有良好的效果，但是会消耗大量的求解时间，缺乏实际应用价值。

变种群模因算法（Variable Population Memetic Algorithm，VPMA）［11］在传统模因算法的基础上，增加了种群规模改变策略，为求解大规模组合优化问题提供了一个通用的解决框架。本文尝试将VPMA 应用于求解大规模配电网重构问题。针对配电网重构问题的特点，在VPMA框架中引入启发式算法中的开关组思想，应用改进开关组法确定两个初始个体及其邻域搜索空间，进而在种群交叉环节引入双主干交叉算子，从而使得个体的优良特征得以保留，应用禁忌搜索法在邻域空间内进行局部搜索，采用动态变更种群规模的方式提高全局搜索能力。最后，在IEEE33、Taipower84、Bus119、Bus136、Bus417 五个不同规模的系统中进行配电网重构仿真，并与多个算法进行比较，验证算法性能。

1 配电网重构的数学模型

本文研究的重点在于提出一种算法解决大规模配电网重构问题。因此，数学模型以常用的系统有功网损最小为优化目标。配电网重构的数学模型如下：

式中：NE为闭合支路的集合；Pk，loss为支路k的有功功率损耗；rk为支路k的电阻；Pk、Qk、Uk为支路k的首端有功、无功功率和电压幅值；A 为节点-支路关联矩阵；P为馈线潮流向量；D 为负荷需求向量；Sk为流过支路k的功率；Sk，max为支路k的线路容量；m为节点总数；Ui、Ui，max、Ui，min分别为节点i的电压及上下限；l为闭合支路总数；d（i，isubstation）为节点i到电源节点isubstation距离。式（1）为目标函数；式（2）为潮流约束；式（3）为支路容量约束；式（4）为节点电压约束；式（5）是保证网络为辐射网的必要条件；式（6）表示节点i与电源节点间的距离是一个有限值，即网络无孤立节点。式（5）、（6）共同组成了的网络的辐射状约束以及连通性约束。

2 VPMA的基本框架

VPMA从仅包含两个个体的初始种群出发，利用种群交叉和局部寻优策略增强算法的局部探索能力，利用种群规模改变策略增强全局搜索能力。VPMA基本框架的流程如图1 所示，其中包含种群初始化、种群交叉、局部寻优、种群更新和种群规模改变5 个步骤。首先在种群初始化环节产生两个个体作为初始种群；随后在种群交叉环节中，种群中的个体两两交叉得到子代集合；选取最优子代进入局部寻优环节进行进一步优化；局部寻优后获得的个体替换种群中的较劣个体从而完成种群更新；当算法陷入搜索停滞，即最优个体经历预设次数的迭代后仍未更新时，VPMA 根据当前种群大小动态调整种群规模，重新执行种群交叉、局部寻优等操作，直到满足收敛条件后输出最终结果。

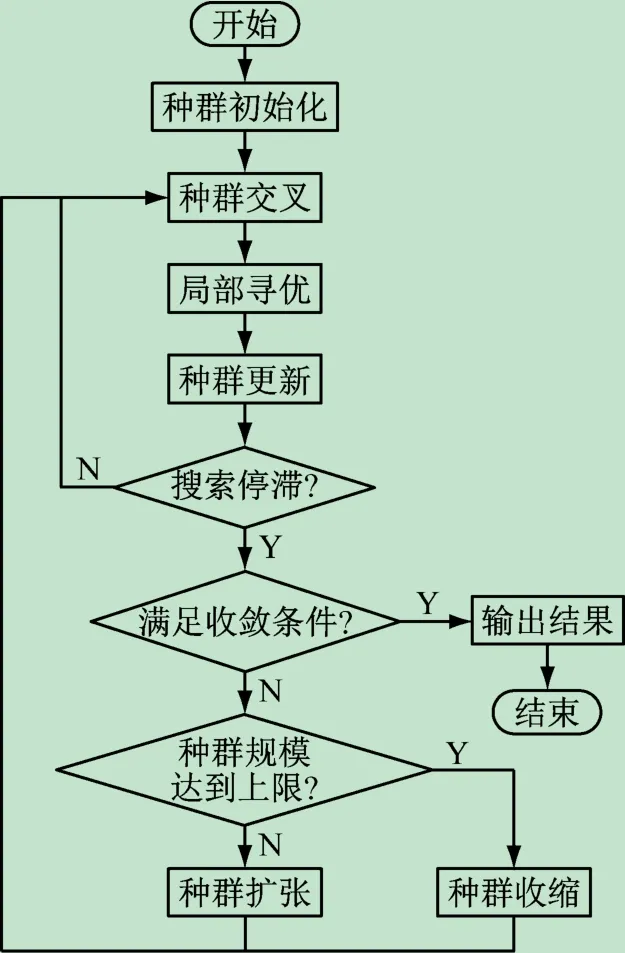
图1 变种群模因算法基本框架流程图

3 VPMA的配电网重构

3.1 配电网重构编码策略

本文采用基于基本环路的编码策略［12］，种群中的个体X 以n维向量的形式表达，即X =［x1，x2，…，xn］T，其中n为个体的维度。策略中个体的维度等于配电网中的基本环路数，大幅降低了变量维度，提高了计算效率。

文献［13］中提出的环路搜索算法能够通过逐步加入余枝的方法，高效地搜索到网络的基本环路。利用贪婪思想优先加入能构成包含最小支路数的基本环路的余枝，使搜索到的环路包含的边数量最少。图2所示是以IEEE16 节点系统为例的搜索及编码过程。具体步骤如下：

（1）从一个完全闭合的网络出发，如图2（a）所示，以电源节点（节点1）为根节点，应用广度优先搜索生成广度优先树，该树的任意节点到根节点距离最短，如图2（b）所示。

（2）利用贪婪思想，优先加入能构成包含最小支路数的基本环路的余枝，并记录余枝与基本环路的对应关系，直至所有余枝都加入网络，完成对基本环路的搜索。如图2（c）～（e）所示，加入余枝的顺序为：8 ～12、7 ～9、5 ～14。分别构成包含支路数5、6、7 的基本环路。

图2 基本环路搜索过程

（3）在示例系统中，基本环路数为3，则个体X可表示X=［x1，x2，x3］T，x1的取值集合为整数［1 5］，分别对应环路1 中开关1 ～6、6 ～8、8 ～12、12 ～11、11～1 的编号（编号可以是任意的）。同理，x2的取值集合为整数［1 6］，x3的取值集合为整数［1 7］，当xn取值为p时，表示环路n中编号为p的开关断开。

3.2 改进开关组法的种群初始化策略

VPMA应用种群初始化环节生成仅包含两个个体的初始种群P=｛X1，X2｝。初始种群理论上既可以随机生成，也可以通过快速的寻优算法搜索得到。将较优的精英个体作为初始种群更符合VPMA的思想，原因是此时搜索刚刚开始，需要在完整的搜索空间中迅速定位到解质量较高、比较有希望出现最优解的搜索区域，再利用局部寻优策略对该区域进行探索，而仅通过局部寻优策略确定搜索方向是非常耗时的。因此能迅速确定搜索区域成为了对种群初始化环节的要求。

开关组法是一种用于求解配电网重构的启发式方法［14］，此方法原理简单、速度快并有较好的寻优性能，但是仅适用于基本环路数少的小规模系统。本文保留原方法中开关组的思想，改变其搜索方式来适应VPMA的基本框架，作为种群初始化环节中生成初始种群的方法。

开关组法将每个联络开关和其左右相邻的2 个分段开关同时考虑。这3 个开关中必须断开一个，闭合另外两个以保持辐射状结构。因此共有3 种可能的开关状态组合，这3 种状态构成了一个开关组。若系统中有k个联络开关，则共有k个开关组形成3k个开关组合。然而，当k增大时，开关组合的数量呈指数型增加，会导致计算负担过重甚至无法计算，这显然不符合快速产生高质量初始种群的要求。因此本文针对大规模配电系统对开关组法进行改进，整体思想为将所有开关组分组处理、随机重组生成初始种群，具体步骤如下：

（1）确定开关组。对一个所有开关都闭合的网络进行环路搜索后，确定其基本环路和对应的余枝。将搜索到的所有余枝看作网络初始的联络开关，根据联络开关在基本环路中的编号可以形成初始解，结合左右相邻分段开关即可确定开关组。

（2）分组。设系统中有k个开关组，k1个为一组，随机分为k2=［k/k1］+1 组，其中［］为向下取整符号。前k2-1 组中每组包含k1个开关组，第k2组中包含k3=Kmodk1（k3≤k1）个开关组，其中mod为取余符号。

（3）抽取。前k2-1 组每组中均会形成3k1个开关组合，第k2组会形成3k3个开关组合，将这（k2-1）×3k3+3k3组合以组为单位，前k2-1 组每组中不重复的抽取一个开关组合，第k2组按同样的方式抽取，但由于第k2组包含的开关组合数较少，抽取完毕后可重复抽取，不影响算法性能。

（4）组合。抽取出的k2个开关组合按照其在模因序列中对应的位置可组合成一个完成的个体。

（5）反复执行步骤（3）共3k1次，即可获得包含3k1个个体的候选初始种群，对所有开关组合进行评价，从中选取两个精英个体（目标函数值最小）即可完成种群初始化。

此方法通过对参数k1的设置，可以将生成的候选种群数限制在3k1个，避免了指数爆炸的问题，同时保证了生成种群的多样性，实现了计算负担和全局搜索能力的平衡，在算例测试中具有良好的效果。

3.3 双主干交叉算子的种群交叉策略

种群交叉通过对现有个体的交叉重组，构建新个体，常用的方法有单点交叉、多点交叉、均匀交叉等。但是这些通用的交叉算子往往没有考虑研究问题的特性，搜索效率不高。为特定的研究问题设计专用的交叉算子通常会更加有利于问题的求解，通过交叉方式的设计，子代可以更容易从父代继承优良特征，避免低劣特征，从而提高搜索性能。

本文将双主干交叉算子［15］引入到种群交叉环节，用于解决配电网重构问题，具体方法如下。

令X1、X2为两个父代个体，比较两个体对应位置上的元素，可以将组成个体的所有元素分为共有元素、独有元素和其余元素，其定义如下：

（1）令XA=｛xA1，xA2，…，xAn｝为X1、X2共有元素的集合，xAi=x1i∩x2i（i=1，2，…，n），即X1、X2对应位置上相同的元素，式中n为个体的维数，i为元素在个体中的位置编号（下同）。

（2）令XB=｛xB1，xB2，…，xBn｝为X1、X2独有元素的集合，xBi=（x1i∪x2i）/（x1i∩x2i）（i=1，2，…，n），即X1、X2对应位置上不同的元素，式中/为差集符号，即第一个集合减去第二个集合包含的元素（下同）。

（3）令XC=｛xC1，xC2，…，xCn｝为X1、X2其余元素的集合，xCi= Xi/（x1i∪x2i）（i=1，2，…，n），即未在X1、X2中出现，但在取值集合中的元素，其中Xi是位置i处元素的取值集合。

根据给定的父代个体，子代个体经由以下3 步形成：

（1）子代继承父代所有的共有元素，形成子代的第1 个主干。

（2）将不同位置上的独有元素相互结合，形成子代的第2 个主干，第1 主干和第2 主干按照对应位置组合即可得到完整的子代个体。其中，第2 主干的个数决定子代集合中的个体数，即若XB中包含j个不为∅的集合，则共会生成2j个子代个体。

（3）在两个主干组合时，第2 主干中的独有元素会有sp的概率变异成新的元素，随机抽取XC中的其余元素作为新元素，本文中sp取值为0.2。

3.4 禁忌搜索的局部寻优策略

局部寻优环节关系到算法的局部探索能力，是VPMA中重要的组成部分。局部寻优策略的好坏决定了算法对某一特定区域的搜索是否充分。局部寻优环节可以采用多种搜索策略，例如爬山法、模拟退火法、禁忌搜索法等，由于禁忌搜索具有搜索范围广、收敛速度快、能够避免陷入局部最优解等特点，本文在局部寻优环节中采用禁忌搜索策略。

禁忌搜索是一种基于局部邻域搜索的逐步寻优策略，其本质上是不断向目标函数数值下降方向进行搜索，优势在于引入了禁忌表和禁忌准则，以此避免陷入局部最优，搜索更多区域。其关键参数有：邻域结构、禁忌表、禁忌长度、藐视准则和终止判据。本小节将给出局部寻优环节关键参数的设置及具体流程。

3.4.1 邻域结构

种群交叉环节完成后，对子代集合中的最优个体进行局部寻优。本文通过对个体每维坐标中的元素执行加1 和减1 的操作来形成邻域结构，对应在网络拓扑中则表现为联络开关在其所在的基本环路中向左右相邻开关的移动操作。设个体为［2，3，4］T，则对应的邻域集合为｛［1，3，4］T，［3，3，4］T，［2，2，4］T，［2，4，4］T，［2，3，3］T，［2，3，5］T｝，取邻域集合中的最优个体作为候选解，进行下一次搜索。

3.4.2 禁忌表与禁忌长度

禁忌表和禁忌长度的设置是禁忌搜索策略的核心所在。本文将禁忌对象设置为历次迭代过程中搜索到的最优个体，禁忌长度TL=20，每搜索一次禁忌对象的禁忌长度减1，当禁忌长度为0 时从禁忌表中解禁。

3.4.3 禁忌搜索的藐视准则和终止判据

为应对搜索过程中出现的所有候选解均被禁忌的情况，设置了藐视准则，即当候选解集中出现优于当前最优个体的候选解时，忽略其禁忌属性，直接设为新的当前最优个体并将其禁忌长度调整为最大。规定终止判据为当前最优个体持续迭代次数Ic大于最大持续次数Icmax。

3.4.4 局部寻优搜索流程

局部寻优环节具体搜索流程如下：

（1）令种群交叉后产生的子代集合中的最优个体为禁忌搜索的当前最优个体，设置关键参数Icmax=3，TL=20，Ic=0，禁忌表为∅。

（2）以当前最优个体为中心，生成邻域集合，并选取邻域集合内的最优个体作为候选解。

（3）判断候选解是否满足藐视准则，若满足，则直接将候选解取为当前最优个体并将其禁忌长度调整为最大；若不满足则判断其是否在禁忌表中，若在禁忌表中则将邻域解集内非禁忌对象中的最优个体取为当前最优个体，若不在则将候选解取为当前最优个体并加入禁忌表，迭代次数Ic=Ic+1。

（4）判断是否满足终止判据，若满足，则结束禁忌搜索，对当前最优个体进行种群更新操作；若不满足，则返回步骤（2），同时禁忌表内所有对象的禁忌长度减1。

3.5 种群更新策略

局部寻优环节优化后的个体将经过种群更新环节决定是否重新插入原种群，本文采用的策略为：若子代个体不与原种群中的任意个体相同且优于其中最劣个体，则替换最劣个体。同时引入变量g记录种群更新停滞次数，当种群未得到更新，即子代个体未重插入种群时，g=g+1；当种群得到更新时g=0。当g达到最大停滞次数gmax时（本文设置为5），算法陷入了搜索停滞，此时进入种群规模改变环节。

3.6 种群规模改变策略

3.6.1 种群规模扩张策略

当搜索陷入停滞时，算法通过引入新个体的方式增大种群规模，达到增加种群的多样性，跳出搜索停滞。本文设定每进入一次种群规模扩张环节，在种群中增加一个新的精英个体。每个新个体都遵循3.2 ～

3.4 小节的方法产生，但只有当新个体不与原种群中任意个体相同时才会加入种群。

3.6.2 种群规模收缩策略

种群规模过大有利于增加种群多样性的同时也意味着更重的计算负担，因此引入最大种群规模pmax，当种群规模扩张到最大时，将执行种群规模收缩策略，缩小种群规模。种群规模收缩的意义在于：①种群规模过大会消耗大量计算资源，形成巨大的计算负担，降低搜索效率；②当种群规模过大但搜索仍陷入停滞时，意味着算法在当前搜索区域内已搜索殆尽，无法搜索到更优解，需要开拓新的搜索区域。

将种群收缩为只包含两个精英个体的小种群，保留原种群中的最优个体作为其中一个精英个体，另一个精英个体遵循3.2 ～3.4 小节的方法产生。通过混合历史最优个体和高质量的新个体，新种群将会继承过往的搜索成果并开拓新的搜索区域。pmax是算法中十分重要的参数，它能平衡计算负担与种群多样性，并决定搜索轨迹和算法性能，pmax在不同规模的系统中宜取不同的值。

3.7 终止判据

本文采用的终止判据为算法搜索到的最优个体连续保持不变的迭代次数t达到最大迭代次数tmax，tmax的取值与网络规模和算法性能要求有密切的关系，其值过小时，会导致无法充分遍历搜索空间，陷入局部最优；其值过大时，会导致搜索到最优解后难以跳出循环，降低搜索效率。

4 算例分析

选用IEEE33、Taipower84、Bus119、Bus 136 和Bus 417 节点系统验证算法性能［16］，基本数据如下：

（1）IEEE33 节点系统额定电压12.66 kV，共33个节点，37 条支路，5 个基本环路，总负荷3 715 kW+j2 300 kvar。（2）Taipower84 节点系统额定电压11.4 kV，共84 个节点，96 条支路，13 个基本环路，总负荷28 351 kW+j20 700 kvar。（3）Bus119 节点系统额定电压11 kV，共119 个节点，133 条支路，15 个基本环路，总负荷22 710 kW+j17 041 kvar。

（4）Bus136 节点系统额定电压13.8 kV，共136个节点，156 条支路，21 个基本环路，总负荷18 314 kW+j7 932.5 kvar。（5）Bus417 节点系统额定电压10 kV，共415 个节点，473 条支路，59 个基本环路，总负荷27 958 kW+j13 237 kvar。

4.1 VPMA法与其他算法性能比较

算法在各系统中的参数设置如表1 所示。

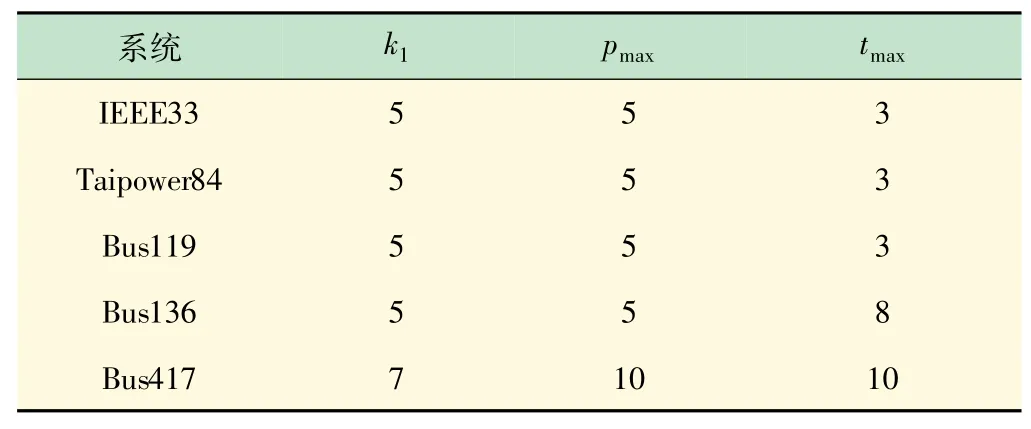
表1 不同系统中参数设置

表2展示了VPMA的运行结果以及与开关断开与交换法（Switch Opening and Exchange Method，SOE）、最小生成树法（Minimum Spanning Tree，MST）、局部搜索算法（Local Search，LS）和混合整数非线性规划法（Mixed-integer Nonlinear Programming，MINLP）的比较。表3 展示了由VPMA求得的各网络最优重构结果。

表2最优网损一行中IEEE33、Taipower84、Bus119和Bus136 系统的最优网损为公认全局最优网损［17］，Bus417 系统的最优网损为文献［10］应用混合整数线性规划法求出的最小网损。Bus119 系统［18］由于原数据中出现多处网络图与数据表不吻合的情况，故许多文献中的计算结果不一致。本文算法以及与之比较的其他算法均采用的是文献［16］中的数据以及网络拓扑。表2 括号中的值为所得网损的相对误差，计算方法为

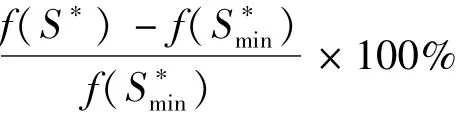
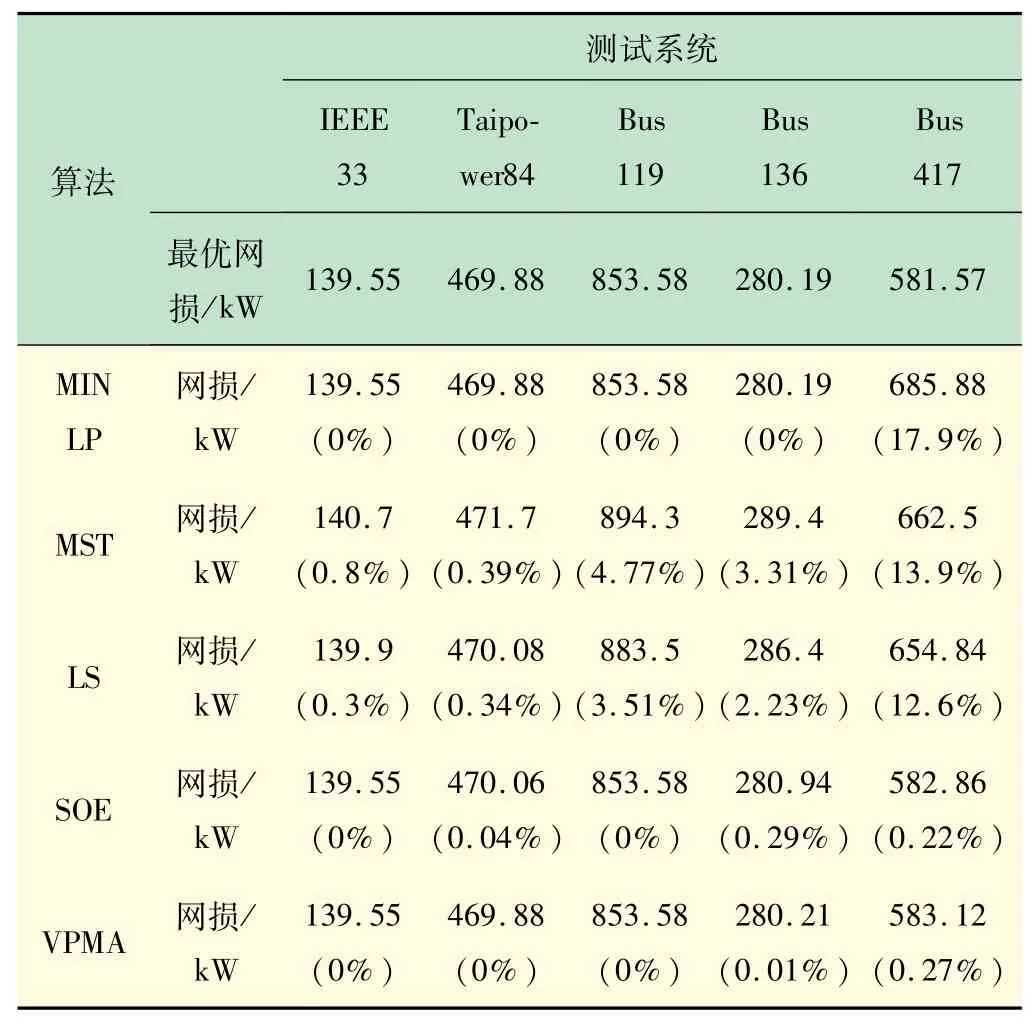
表2 不同算法结果比较

表3 VPMA法求得各网络最优重构结果

其中：f（S*）为算法计算出的网损；f（S*min）为最优网损。

由表2 可以看出，VPMA在求解不同系统时，相对误差在0% ～0.27%，说明了其在不同规模的系统中均有较高的精确度。在求解IEEE33、Taipower84、Bus119 系统时，VPMA 与MINLP 均能获得最优解，而MST、LS、SOE 获得的解有不同程度的相对误差。在Bus 136 和Bus 417 系统中，VPMA 分别有0.01%和0.27%的相对误差，均低于MST 和LS；MINLP 在Bus136 系统的相对误差比VPMA低0.01%，但在Bus 417 系统中比VPMA 高17. 63%，说明VPMA 较MINLP有更好的求解大规模系统的能力。SOE 在Bus136 系统的相对误差比VPMA 高0. 28%，在Bus 417 系统中比VPMA 低0.05%。SOE 代码可在文献［9］中获得，本文将SOE 和VPMA 代码运行在带有Intel（R）Core（TM）i7-5500U CPU@2.4 GHz 处理器，12.0GRAM的计算机系统MATLAB 软件中，分别运行100 次，运行结果如表4 所示。

表4 VPMA法与SOE法结果比较

对VPMA与SOE在平均网损、最优解比例和平均耗时三方面的性能进行比较。在表4 平均网损一栏中，VPMA与SOE 在IEEE33 和Bus119 系统中的结果相同且与最优解相等。在Taipower84 和Bus136 系统中VPMA结果比SOE低0.04%和0.28%。在Bus417系统中两者相差0.05%，说明两者均具备求解大规模配电网重构的能力，且在节点数少于417 的系统中VPMA优于SOE，在Bus417 节点系统中SOE求得的解略优于VPMA。在最优解比例一栏，SOE 仅在IEEE33和Bus119 系统中可求得最优解，其余系统均无法获得最优解。VPMA在IEEE33、Taipower84 和Bus119 系统中最优解比例均为100%，在Bus136 系统中比例为40%，在Bus417 系统两种方法均获得了与最优解近似的次优解。可见对于大型复杂网络，VPMA 获得的最优解比例明显高于SOE。在平均耗时一栏，VPMA 在除Bus136 系统外的不同规模系统中耗时均明显少于SOE，平均耗时缩短了21.6% ～80.4%；在Bus136 系统中，VPMA虽耗时较长，但其平均网损降低，最优解比例明显提高，SOE 在求解Bus136 系统重构问题时，快速收敛到误差较大的次优解，说明其没有对搜索空间进行充分探索。可见在求解大规模配电网重构问题时，VPMA较SOE效率更高。综上所述，VPMA 较其他同类算法速度快、精度高，在求解大规模配电网重构问题中有明显的优势。

4.2 VPMA中不同步骤的影响

VPMA的基本思想为应用种群初始化环节快速搜索出较好的精英个体，进而应用局部寻优环节进一步优化个体，随后通过种群规模扩张和种群规模收缩环节增加种群多样性，最终确定最优个体。

为分析以上4 个步骤对算法性能的影响和在搜索最优解过程中的贡献，本节将分析执行以上各步骤后的时间消耗和系统网损。定义VPMA Ⅰ为算法执行种群初始化环节之后的结果；VPMA Ⅱ为执行种群初始化和局部寻优环节后的结果；VPMA Ⅲ为执行种群初始化、局部寻优和种群规模扩张环节后的结果；VPMA Ⅳ为执行种群初始化、局部寻优、种群规模扩张和种群规模收缩，即完整算法后的结果，如表5 所示。

表5 5 个系统由VPMA法不同步骤获得的网络重构结果

在表5 的第3、4 列，即在IEEE33 和Taipower84 系统中，VPMA Ⅲ与VPMA Ⅳ的值相同。这是因为在这两个系统中仅经过种群初始化环节和局部寻优环节后，算法即可得到最优解，在种群规模改变环节中仅经历了种群规模扩张环节，没有进行种群规模收缩环节，实际上，种群规模扩张环节中是为了满足收敛条件而在对最优解重复搜索，使得运行耗时增加。对比表5的7、8、9 行，VPMA Ⅱ运行后IEEE33、Taipower84 已求得最优解，Bus119、Bus136 系统最优解比例较低，平均网损较高，Bus417 系统网损误差较大。这说明小系统不能充分挖掘变种群模因算法的求解潜力，仅运行VPMA Ⅱ，即不加入变种群策略的传统模因算法已经有了较好的求解小规模配电网重构问题的能力，但还不足以求解大规模配电网。

对表5 中的5、6、7 列，即对3 个大规模配电网进行分析可知，VPMA Ⅱ运行后将Bus119、Bus136、Bus417 系统网损误差分别从6.6%、32.3%和34.2%降低到了0.3%、0.7%和4.98%，Bus119 和Bus136 最优解比例由0%提高到了76%和9%。VPMA Ⅲ运行后将以上3 个系统网损误差分别降低到了0%、0.01%和0.71%，前两系统最优解比例提高到100%和19%。VPMA Ⅳ运行后将以上系统网损误差分别降低到了0%、0.01%和0.27%，前两系统最优解比例提高到了100%和40%。由此可知，对于Bus119 系统执行VPMA Ⅲ即可搜索到全局最优解而无需经过种群规模收缩策略，而Bus136 和Bus417 系统在VPMAⅢ运行后的平均网损和最优解比例仍有提高的空间，在完整算法运行后进一步降低了平均网损并提高了最优解比例。

对表5 中各步骤的平均耗时进行分析可知，VPMA Ⅰ耗时占总时耗时0.4% ～15%，生成的解平均误差1.2% ～34.2%，且系统规模小时，耗时比例较大、解误差较小，系统规模大时，耗时比例小、解误差较大。说明其能在不同规模系统中平衡求解速度和个体质量，满足3.2 小节中所述对种群初始化环节迅速定位到解质量较高的搜索区域的要求。在大规模系统中，VPMA Ⅲ和VPMA Ⅳ耗时占总耗时的80.4% ～97.2%，说明种群规模扩张和种群规模收缩策略占据了算法大部分的搜索时间，是算法最耗时的部分，同时也是求解大规模配电网重构问题最关键的步骤，算法通过对种群规模的不断调整从而增加种群多样性、充分探索搜索空间，得到最优搜索结果。

5 结 语

引入变种群模因算法的框架，构建了求解大规模配电网重构问题的方法。该方法根据配电网重构问题的特点，引入启发式算法中的开关组思想生成初始种群并确定其邻域，应用智能算法中的双主干交叉算子和禁忌搜索算法作为种群交叉及局部寻优策略，采用动态改变种群规模策略。所提方法在一个基本框架中将启发式算法的思想与人工智能算法相结合，使得其兼具了启发式规则原理简单、求解速度快的优势和人工智能算法搜索能力强的特性。最后，在IEEE33、Taipower84、Bus119、Bus136、Bus417 五个不同规模的系统中进行配电网重构仿真，并与多个算法进行比较，验证了算法性能。同时分析了算法各个步骤对搜索过程的影响，证明了所提出的方法求解速度快、结果质量好，适合求解大规模配电网重构问题。