多旋翼无人机减振分析与实验

2022-08-06马维力和英鹏崔辉如李道奎申柳雷

国防科技大学学报 2022年4期

马维力，和英鹏，崔辉如，李道奎，申柳雷

(1. 长安大学理学院，陕西西安 710064； 2. 陆军工程大学国防工程学院，江苏南京 210007；3. 国防科技大学空天科学学院，湖南长沙 410073； 4. 国防科技大学军事基础教育学院，湖南长沙 410072)

旋翼无人机具备体积小巧、机动能力强、易于携带以及成本低廉等独特优势，在军事和民用领域具备极为广阔的应用前景[1-3]。军用方面，世界各国纷纷布局基于旋翼无人机的协同作战无人机蜂群系统，例如美国国防部高级研究计划局(defense advanced research projects agency，DARPA)的进攻性蜂群使能战术(offensive swarm-enabled tactics, OFFSET)近年来取得突破性进展[4-5]。民用方面，根据《关于促进和规范民用无人机制造业发展的指导意见》，民用无人机市场规模在2025年将达到1800亿元。现阶段，旋翼无人机呈现小型化、智能化和数字化的发展趋势。现实需求对无人机综合性能提出更高要求，机身振动对无人机性能的影响日益突出[6-8]。当前关于旋翼无人机的研究主要集中在导航与控制方面，机身振动与优化设计的工作有限。

旋翼无人机机身振动过大，会产生诸多严重问题，包括影响惯性测量单元的测量精度，导致飞行状态不稳，影响有效载荷工作状态，容易造成结构疲劳损伤和多余的能量耗散，导致航时降低等[9]。因此，有必要将无人机减振分析与优化设计工作融入已有研发体系，形成标准化工作流程，指导相关工作开展。

得益于微电子(micro-electro-mechanical system, MEMS)技术发展，旋翼无人机行业近年来得以快速发展。国内外关于旋翼无人机振动控制技术研究也于近几年逐渐开展。国内方面，王伟等[10]针对小型多旋翼无人机的机体设计，提出了标准化设计方法；段鹏飞等[11]基于被动隔振理论，提出了某型号无人机光电吊舱的隔振方案，通过振动实验，验证了所提方案的有效性，其研究成果为旋翼无人机有效载荷的隔振系统设计提供依据；刘峰等[12-14]基于有限元方法，开展了碳纤维无人机和重载多旋翼无人机的强度分析、稳定性分析和优化设计工作，同时开展了复合材料铺层的优化设计工作；裴彦华等[15]基于谐响应仿真分析，通过研究振动传递路径，确定了某型号无人机不同传递路径对机载传感器振动的贡献量；基于计算流体力学(computational fluid dynamics, CFD)仿真分析技术，叶建川等[16-17]研究了气动力对四旋翼无人机模态的影响，结果表明由于气动力对桨叶外形产生影响，无人机前飞状态和悬停状态的模态存在显著区别。国外方面，Semke等[18]对当前军用市场多架小型无人机(包括旋翼和固定翼)的振动环境进行了综述，重点关注通过实验采集机身振动数据，评估其对有效载荷和图像数据采集的影响；针对无人机机身振动导致图像模糊这一常见问题，Swetich与Semke[19]通过开发程序插件，在特定时间段控制动力单元的启停，实现图像数据采集系统性能最大化应用；Misiorowski等[20]基于Navier-Stokes分离涡模型，研究了四旋翼无人机在摆振飞行条件下的性能；Hwang等[21]采用三维非结构网格流动求解器，利用数值计算方法，研究了多旋翼无人机气动性能及其旋翼与机身之间的气动相互作用；Kolaei等[22]通过风洞试验，不同入流角度下对动力单元进行风洞测量，完成了一种小型无人机旋翼性能特性的实验和理论分析；Ranjan等[23]将无线电遥控微型直升机改装成具备图像数据采集功能的自主微型无人直升机，并从隔振的角度对机体不同位置的振动进行了测量和分析。通过捕捉直升机的基线振动剖面，验证了被动隔振器在无人直升机光电有效载荷减振方面的有效性。

关于无人机机身振动的问题，现阶段的研究多采用仿真分析与实验相结合的方法，通过优化主动隔振和被动减振的方法，实现减少机身或有效载荷振动的目的。本文重点关注机身结构分析与优化设计在无人机减振方面的应用。针对某型号无人机机身振动过大导致飞行状态不稳的问题，系统开展基于CAE仿真技术与实验方法的机身振动控制分析研究。确定了共振频点及其对应振型，针对性开展优化设计，通过优化机身壳体截面形状，在不增加质量的前提下，显著提高无人机系统的固有频率，有效规避了共振现象。

1 理论模型

1.1 无人机模型

本文所研究的四旋翼无人机布局方式如图1所示，除无人机机身壳体外，主要部件包括起落架、电机、电池、云台、电路板等。

图1 无人机布局方式Fig.1 Layout of the multi-rotor drone

四旋翼无人机包括四个动力单元，每个动力单元包含一个电机和一个桨叶，提供升力的同时承受阻力、侧向力和扭矩。悬停时，电机转速约为6 000 r/min。

1.2 模态分析与共振理论

考虑阻尼的无人机系统自由振动的平衡方程为：

(1)

其中：M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；δ为位移。

当不考虑阻尼结构时，式(1)的解为：

δ=ψsin(ωt+θ)

(2)

其中：ψ为特征向量大小；ω为固有频率；t为时间；θ为相位角。

通过数学方法，求解式(2)，可得

(3)

求解式(3)得n个固有频率的值。一般而言，与高阶固有频率相比，低阶固有频率更易被外界激励激发。因此工程分析中，通常只需考虑低阶固有频率的共振问题。

图2为旋翼无人机发生共振的机理。旋翼无人机依靠电机带动桨叶产生升力，同时会产生周期性气动力和动不平衡产生的周期性振动激励，成为无人机主要振动激励源。其激励频率为：

(4)

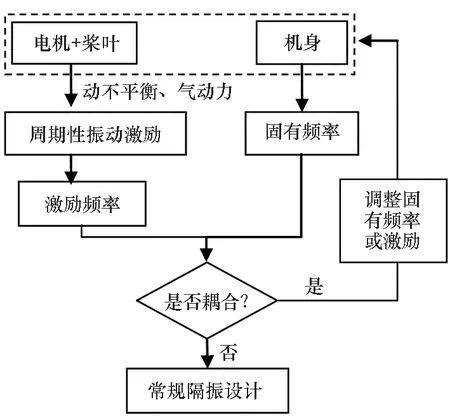
图2 旋翼无人机共振机理Fig.2 Resonance mechanism of rotor UAV

其中，n为动力单元转速，z为桨叶数量。若激励频率与机身固有频率的值相差较大，则不会发生共振，只需进行常规隔振设计即可(包括主动减振、被动隔振和带阻尼滤波等)。但是，若振动激励频率与机身固有频率接近甚至相等，则会发生共振现象，严重影响飞行安全。此时需要调整激励频率或者机身固有频率，实现错频设计，避免共振。

当系统同时具备两个因素时，会引发结构共振：一是激励频率与结构固有频率接近；二是激振力可以克服结构阻尼，增大结构振动的振幅，甚至破坏结构。周期性激励可以写成正弦形式，即：

(5)

(6)

由于式(6)最后一项的值随着时间增大不断增大，当达到临界点时，足以导致结构破坏。因此，结构共振的危害是巨大的，必须避免结构发生共振。一般情况下，激励频率与电机、桨叶型号和飞控策略有关，调整幅度有限，难以实现有效错频设计。因此，在研发设计定型阶段前调整机身固有频率，实现错频设计，是无人机研发流程中的重要环节。

2 CAE建模与数值计算

2.1 网格划分

基于MSC.Patran商业有限元软件，对多旋翼无人机几何模型进行网格化处理。对于壳体结构采用四边形壳单元建模，电路板采用六面体实体单元建模，电机、电池、云台等结构采用集中质量点单元建模，利用多点约束单元(multi-point constrain, MPC)单元模拟集中质量约束关系。所建有限元模型如图3所示。

图3 无人机有限元模型Fig.3 Finite element model of multi-rotor UAV

2.2 材料性能拉伸实验

为确保有限元仿真数值计算精度，通过材料拉伸实验获得无，试样及实验装置如图4所示。

(a)哑铃型实验件 (b)拉伸实验装置(a)Dumbbell type test piece (b)Tensile test device图4 材料拉伸哑铃型试样及实验装置Fig.4 Samples and experimental devices

安排五组对照实验，实验结果如表1所示。其中，E、υ和σb分别为材料弹性模量、泊松比和拉伸强度。

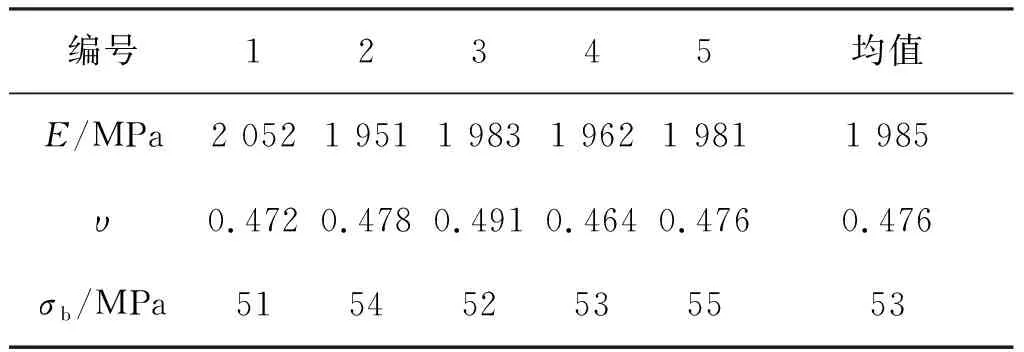
表1 材料拉伸实验结果Tab.1 Tensile test results of materials

2.3 模态分析

采用MSC.Nastran对图3所示无人机模型进行模态分析，得到无人机结构的前五阶整体振型对应的固有频率，如表2所示，仿真结果的前五阶频点对应振型如图5所示。

表2 无人机前五阶整体振型对应仿真固有频率Tab.2 The first five-orders natural frequencies

(a) 第一阶 (b) 第二阶(a) The 1st order (b) The 2nd order

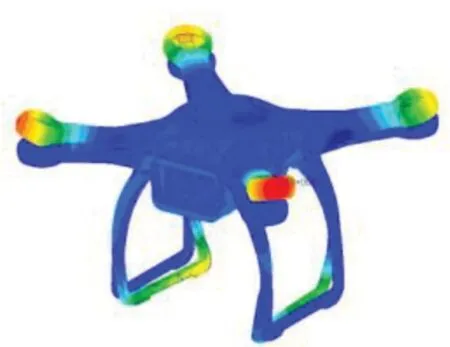
(e) 第五阶(e) The 5th order图5 无人机前五阶整体振型仿真结果Fig.5 Simulation results of the first five-orders mode shape

3 模态实验

模态实验中，采用HBM MGCplus 动态数据采集系统和SDI(silicon designs inc)单向加速度传感器(10个)。利用四根柔性绳悬挂的方式模拟无人机结构飞行时自由的边界条件，如图6所示。激励方式采用锤击激励方式，利用加速度传感器测试记录各个测点在冲击荷载作用下动力响应，加速度传感器主要布置在四个悬臂上。联合所有测点加速度响应，采用随机子空间方法分析得到结构振型及对应的频率。无人机前五阶整体振型对应的实验固有频率如表3所示。

图6 模态实验方案Fig.6 Devices of the modal test

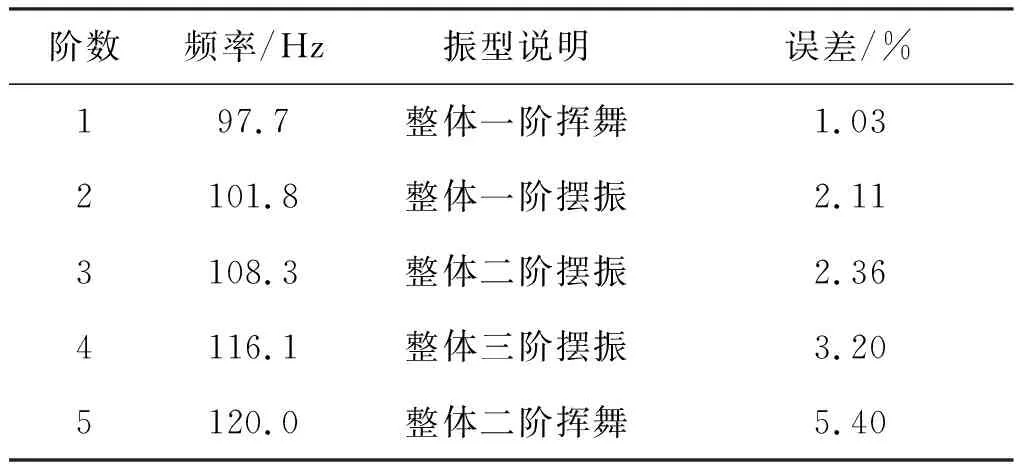
表3 无人机前五阶整体振型对应的实验固有频率Tab.3 Experimental results of the first five-orders natural frequencies

实验结果的前五阶频点对应振型如图7所示。

(a) 第一阶(a) The 1st order (b) 第二阶(b) The 2nd order

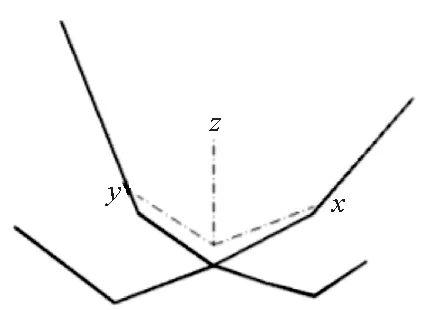
(e) 第五阶(e) The 5th order图7 无人机前五阶整体振型实验结果Fig.7 Experimental results of the first five-orders mode shape

4 结果讨论

4.1 频率结果分析

对比表2和表3中的数据，结合图5和图7中的模态振型，可以发现有限元仿真结果与模态实验结果相比，频点大小吻合，模态振型一致，验证了有限元仿真结果的正确性。

已知悬停状态下电机转速为6 000 r/min，有限元仿真和模态实验结果表明，前三阶固有频率的值均在100 Hz左右。可知，固有频率与激励频率存在耦合现象，在悬停状态时极易产生共振现象。可以通过调整激励频率或固有频率两种方式，规避共振现象。

4.2 壳体厚度对固有频率的影响

本节通过结构优化设计提高固有频率，达到规避共振现象的目的。机身壳体为无人机结构主体部分，通过改变机身壳体厚度或壳体形状，可以调整其结构刚度，有望达到改变固有频率的目的。

由前文可知，前三阶固有频率与激励频率严重耦合，第四阶及更高阶固有频率逐渐远离激励频率。因此，文章后续讨论部分，仅关心无人机系统的前三阶固有频率。

增加厚度可以增大壳体截面面积，继而提高壳体结构抗弯刚度，有利于针对性地提高机身整体摆振和挥舞模态对应的固有频率。但需要指出的是，壳体质量占机身总体质量的8.7%，当壳体厚度增加时，机身质量也随之增加。分别将机身壳体厚度增加为原厚度的1.2倍、1.5倍和2倍，对改变厚度后的模型进行模态分析，评估机身壳体厚度对无人机固有频率的影响。前三阶整体振型对应的固有频率如表4所示。取1.2倍原厚度时，壳体截面面积增加20%，无人机总质量增加1.7%，前三阶整体振型对应固有频率增加范围介于4.44%～4.86%之间；取1.5倍原厚度时，壳体截面面积增加50%，模型总质量增加4.35%，频率提高范围介于9%～11.06%之间；取2倍原厚度时，壳体截面面积增加100%，整体质量增加8.7%，频率提高范围介于12.41%～16.73%之间。可以发现，增加机身壳体厚度可以提高无人机固有频率，但同时会显著增加无人机结构质量，减少航时。

4.3 机身壳体形状对固有频率的影响

观察前三阶固有频率对应的振型，分别为整体一阶挥舞、整体一阶摆振和整体二阶摆振振型，且主要为机身壳体的挥舞和摆振。因此推断，对机身壳体的横向和竖向截面形状进行优化设计，有望显著调整机身壳体结构刚度，达到调整无人机系统固有频率的目的。其中，横向截面形状由原来的“w”型优化为“抛物线”型，如图8所示。竖向截面形状由原来的“圆弧+直线”优化为“圆弧+切线”形式，如图9所示。横向和竖向截面形状优化设计后，截面面积仅分别增加0.1%和0.2%，因此，结构质量也仅分别增加0.1%和0.2%。

表4 不同壳体厚度对应的固有频率Tab.4 Natural frequencies of different shell thicknesses

(a) 优化前 (b) 优化后(a) Before optimization (b) After optimization图8 结构横向优化设计Fig.8 Horizontal optimization design

(a)优化前 (b)优化后(a) Before optimization (b) After optimization图9 结构竖向优化设计Fig.9 Vertical optimization design

同时改变横向和竖向结构截面形状时，前三阶整体振型对应的固有频率如表5所示。可以发现，同时优化机身壳体的横向和竖向截面形状后，无人机系统的前三阶固有频率增幅介于18.43%～37.23%之间。显然，通过优化机身壳体的截面形状，可以显著提高无人机系统频点，且极小增加系统质量。

表5 同时优化横向和竖向结构形式后的固有频率Tab.5 Natural frequencies of the optimized structure

5 结论

针对某型号旋翼无人机机身系统振动过大导致飞行状态不稳的问题，基于有限元仿真技术与实验方法，开展了振动控制分析研究。确定振动过大的原因为固有频率与激励频率耦合导致的共振现象，确定共振频点的模态振型为一阶挥舞、一阶摆振和二阶摆振振型。通过改变机身壳体厚度，可以提高无人机系统固有频率，但提升幅度有限，并且还会增加结构质量。优化机身壳体的横向和竖向截面形状，可以显著提高无人机系统频点，且极小增加额外质量。