基于改进遗传算法的轧辊磨削产线智能排程方法＊

陆耀珣 王立平 孙丽荣 杨金光 王 冬 李学崑

（①电子科技大学机械与电气工程学院，四川 成都 611731；②清华大学机械工程系，北京 100084；③山东钢铁集团日照有限公司，山东 日照276806 ；④轧制技术及连轧自动化国家重点实验室，辽宁 沈阳 110819）

钢铁行业是支撑国民经济发展的重点行业，而轧辊磨削是轧钢生产的重要组成，轧辊磨削产线的排程方案直接影响轧钢生产的效率。与单一柔性作业车间或天车调度问题不同，轧辊磨削产线需要同时考虑多工件、多工序、多磨床和多天车，属于柔性作业车间调度与天车调度的交叉耦合问题，调度规模大，影响因素多，排程极为困难。传统基于人工经验的专家系统虽能得到可行的排程方案，但无法保证方案的性能最优。如何在“工件-设备-天车”时空耦合的约束下实现高效智能排程，是当前轧辊磨削产线面临的关键问题。

近年来柔性作业车间调度问题与天车调度问题受到国内外学者的持续关注和研究，智能调度排程算法是其中的关键研究内容。已有许多学者针对柔性作业车间调度问题展开研究，如Dang S 等[1]设计了一种改进遗传算法解决了柔性作业车间调度问题；屈新怀等[2]将贪婪算法与遗传算法相融合解决了柔性作业车间调度问题；赵小惠等[3]设计了一种改进蚁群算法解决了柔性作业车间调度问题；蔡敏等[4]融合了粒子群优化算法、模拟退火算法与改进人工蜂群算法，解决了模糊柔性作业车间调度问题。此外也有众多学者针对天车调度问题进行了研究，如许少杰[5]借助遗传算法完成了钢厂天车的建模与调度优化；Meisel F 等[6]将免疫算法与粒子群优化算法相结合，研究了车间天车调度优化问题；徐乐[7]同时使用元胞自动机和遗传算法完成了车间天车优化，其中元胞自动机负责天车建模，遗传算法负责调度任务优化；雷兆明等[8]使用布谷鸟搜索算法优化了车间天车调度；杨坤鹏[9]设计了一种改进遗传算法提高了连铸-热轧板坯车间天车效率，进而提升了入库效率。部分学者进一步考虑调度运输时间，在柔性作业车间中引入单天车系统。例如，Liu Z等[10]以综合能耗为目标函数，使用遗传算法求解包含单个天车的柔性作业车间调度问题。Li J 等[11]提出一种改进Jaya 遗传算法求解考虑运输时间的柔性作业车间调度问题。Wang H 等[12]使用遗传算法求解考虑运输过程的柔性作业车间调度问题。杨帆等[13]在柔性作业车间调度问题中加入运输和装配环节，并提出一种带保优策略的遗传-粒子群混合算法求解柔性作业车间多资源调度问题。但单天车系统回避了多天车干涉这一天车调度问题的核心。多天车之间的干涉与避让导致调度运输时间进一步增加，在天车实时位置未知的情况下时间增量具有不确定性。针对多工件、多工序、多磨床和多天车耦合的复杂作业系统，仍需要深入开展调度排程研究。

本文针对轧辊磨削产线调度问题，提出了一种基于改进遗传算法的智能排程方法，以实现复杂约束下的智能求解。选择最大完工时间作为目标函数，使用三层编码方式分别对工件工序层、机器层和天车层进行编码，使用君主染色体+POX 交叉的选择、交叉方案，采用动态变异率提高后期跳出局部最优解的能力，最后设计了基于动作分解的天车解码规则及系列算子，以实现产线智能排程，并使用自适应采样时间算子提高计算效率。与经过最低限度改进的原始遗传算法及基于人工经验的排程方法对比，所提出的改进遗传算法具有明显优势。

1 问题描述

轧辊磨削产线调度问题可描述为：对于n个工件，其组成的集合为J={J1,J2,···,Jn}，每个工件包含j道工序，则工件i对应工序集合为Oi={Oi1,Oi2,···,Oij}。将所有用于加工工件的生产设备及工位统称为机器，整个轧辊磨削产线的全部m台机器组成机器集合M={M1,M2,···,Mm}，q台天车组成的集合为Q={Q1,Q2,···,Qq}。工件i的第j道工序Oij可用机器集合为Mij∈M。调度的目标是合理安排工件工序、机器、天车使得相关性能指标最优。

轧辊磨削产线中工件、机器和天车需满足时空约束，如式（1）～（10）所示，符号变量如表1 所示。

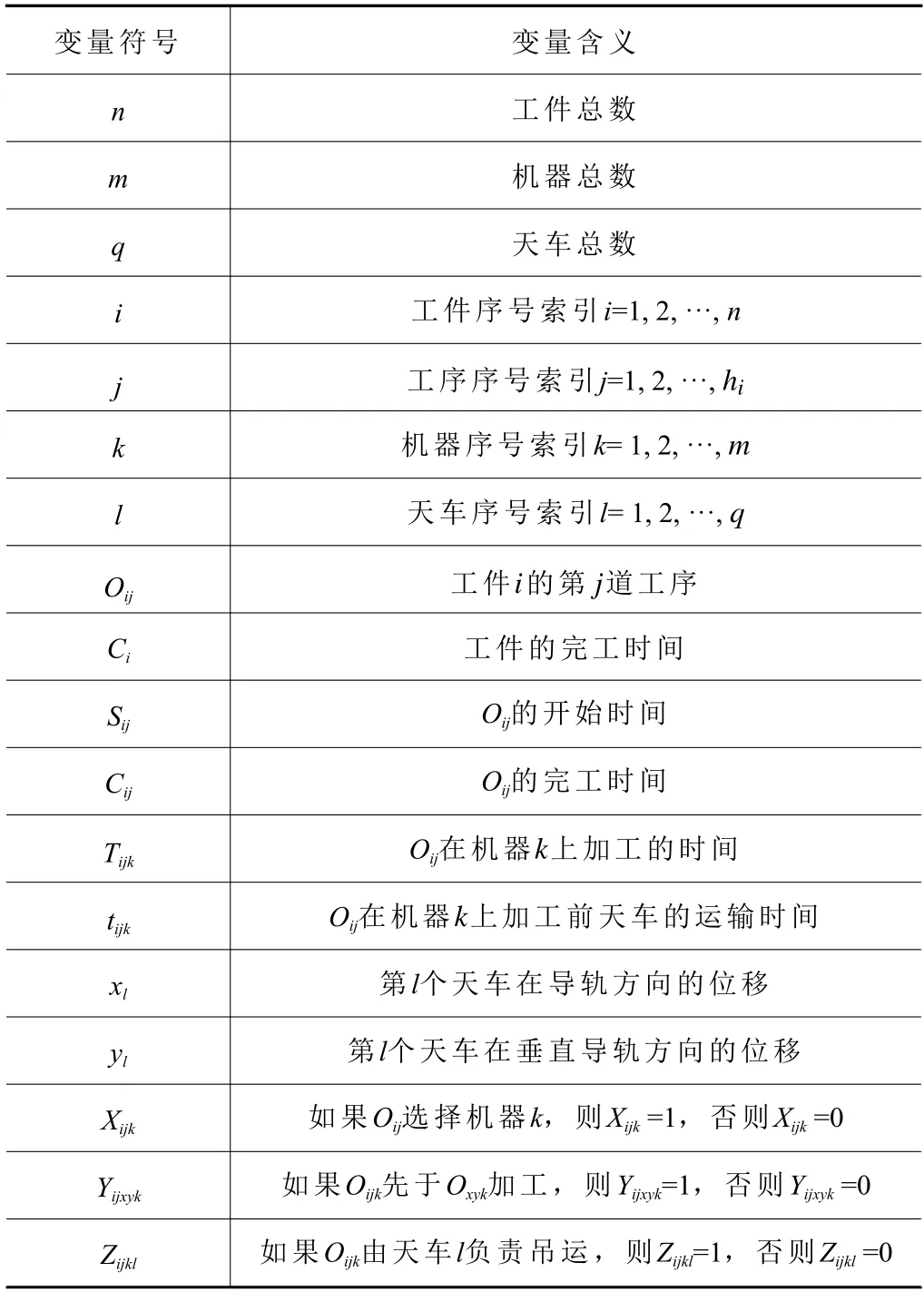
表1 符号变量表

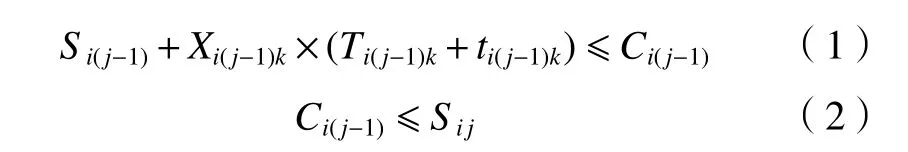
其中：式（1）表示工件某道工序在机器上的开始时间、加工时间、天车运输时间三者之和不超过工件该工序的完成时间。式（2）表示工件某道工序的完工时间不超过下一工序的开始时间。式（1）和（2）联立表示工件加工遵守工序顺序约束。

式（3）表示任一工件加工时间不大于最大完工时间。

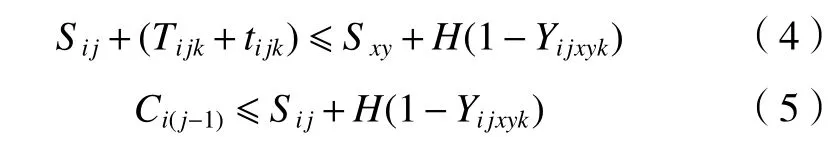
式（4）和（5）中H表示一个很大的数，两式联立表示任一时刻的任一机器只能加工一道工序。

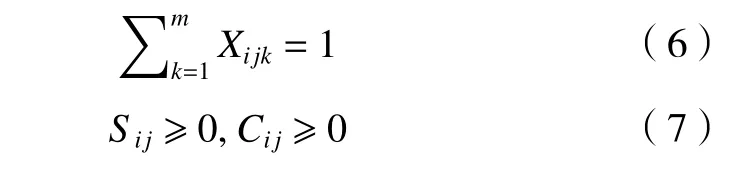
式（6）表示某时刻一道工序只能由一台机器加工。式（7）表示工件加工的开始时间和完成时间非负，且从0 时刻开始任意工件都可以加工。

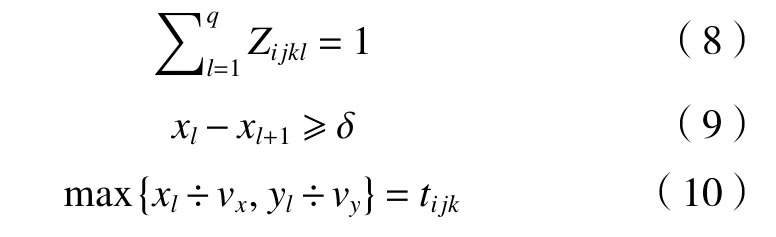
式（8）表示每个吊运任务只能分配一辆天车。式（9）表示天车之间的距离要大于等于安全距离。式（10）表示在机器k上加工前，天车的运输时间应等于天车导轨方向运动时间与垂直天车导轨方向运动时间中的最大值。

本文使用最大完工时间这一广泛应用的性能指标作为约束优化问题目标函数，使求取的排程方案的最大完工时间最小。

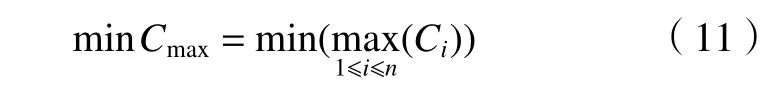
2 改进遗传算法

2.1 算法流程

首先对标准遗传算法进行改进，解决轧辊磨削产线中的工件排程问题，进一步设计基于动作分解的天车无干涉解码规则及系列算子，从而实现工件、机器和天车三者时空耦合条件下的轧辊磨削产线智能排程，其算法流程如图1 所示，其步骤描述如下：

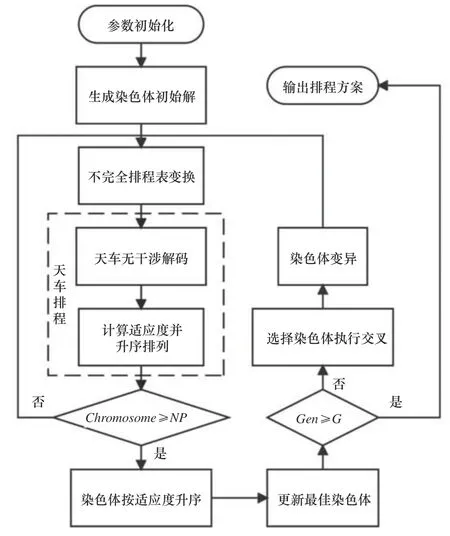
图1 改进遗传算法流程图

步骤1：遗传算法参数初始化。

步骤2：生成多个初始染色体，作为初始种群。

步骤3：遍历初始种群中的每个染色体，对每个染色体执行不完全排程表变换，将染色体变换为包含工件工序与天车任务分配信息，但不包含工件工序与天车任务时间信息的不完全排程表。将不完全排程表作为输入，执行天车解码，得到包含工件工序与天车任务时间信息的完全排程表，并计算适应度。

步骤4：判断染色体是否遍历完成，是则前往步骤5，否则前往步骤3。

步骤5：将染色体按适应度升序，并更新最佳染色体。

步骤6：判断是否到达最大遗传代数G，是则前往步骤8，否则前往步骤7。

步骤7：选择需要参与交叉的染色体，对每个选择的染色体依次执行交叉、变异操作，并返回步骤3。

步骤8：对于最佳染色体，绘制甘特图、算法收敛曲线图、天车位移图，输出完全排程表，改进遗传算法结束。

2.2 染色体编码

本文使用一种三层编码方式，即染色体具有3个基因串，分别为工序顺序层JS、机器选择层MS和天车选择层PS。基因串长度为所有工件与所有工序的数目总和，3 个基因串长度相等，以[JS,MS,PS]的形式首尾连接，如图2 所示。根据每一层的特点，又使用了不同的编码规则，其中JS 使用基于工序的编码规则，MS 使用相对机器编码的编码规则，PS 使用直接编码规则。

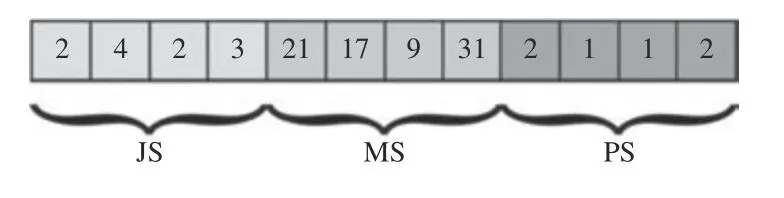
图2 三层染色体编码方式

基于工序编码的编码规则可按如下方式描述：对于工序顺序层JS，其为有序数列，其中第i位上的数字为x，代表工件编号为x。从第1 位起至第i位，x共出现了k次，则JS 的第i位代表Oxk，即工件x的第k道工序。如图3 所示。

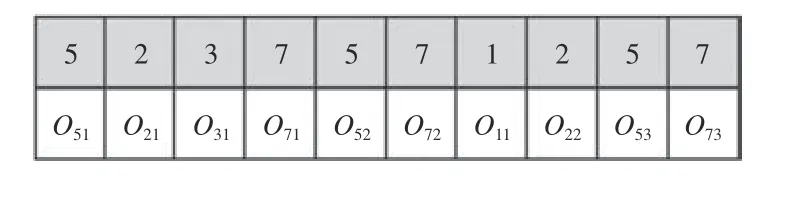
图3 JS 基于工序编码的编码规则

MS 使用相对机器编码的编码规则，可按如下方式描述：对于MS，其为有序数列，从左到右人为规定每一位所对应的工件与工序。对于某一位i，事先设定其对应的工件工序可用的机器集合M，M中的元素为机器编号，则MS 中第i位上的数字MS(i)对应的机器编号为M(MS(i))。如图4 所示。

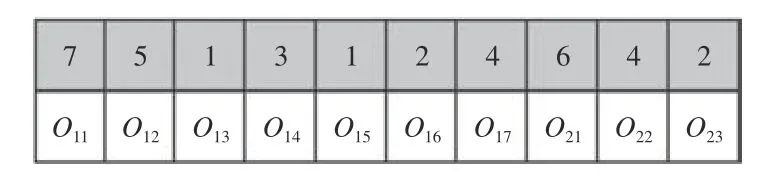
图4 MS 基于相对机器编号的编码规则

PS 使用直接编码的编码方式，基因上的数字即为天车号，对应工序同MS。

2.3 染色体选择与交叉

本文中的选择操作使用了轮盘赌法与精英保留策略；交叉操作中，对于JS 使用了君主染色体方案与POX 交叉相结合的方案，对于MS、PS 使用多点交叉方案。

2.4 染色体变异

对于JS，因受到严格约束，为防止出现不可行解，使用染色体上两个不同基因互换的策略，而对于MS 与PS，使用单点变异策略。

同时，为缓解迭代后期种群陷入局部最优解，使用随迭代次数变化的动态变异率：

其中：Pm为变异率，Pm0为初始变异率，gen为当前迭代次数，G为迭代次数上限。随着当前迭代次数的不断增大，变异率不断增大，能够一定程度上缓解陷入局部最优解的问题。

2.5 基于动作分解的天车解码规则

基于动作分解的天车解码规则是通过模拟天车调度运输的一系列动作，并以一定的采样时间间隔更新天车坐标、天车状态和运动时间，从而实现工件与天车调度排程。天车动作表如表2 所示，表中动作1～8 构成天车一次完整调度动作。分析可知，天车动作可分为两类调度动作，第一类为天车静止动作，此时天车在轨道上保持静止，仅天车上的小车与钩爪可进行运动，放钩、装载、卸载和收钩属于第一类，耗时可视为定值。第二类为天车移动动作，此时天车在轨道上移动，而天车上的小车和钩爪将相对于天车保持静止，前往始发地、前往目的地属于第二类。进一步分析可知，天车前往始发地与前往目的地本质是一个动作，皆为从轨道上一点移动至另一点。此外，第二类天车动作耗时与天车速度及位移有关。

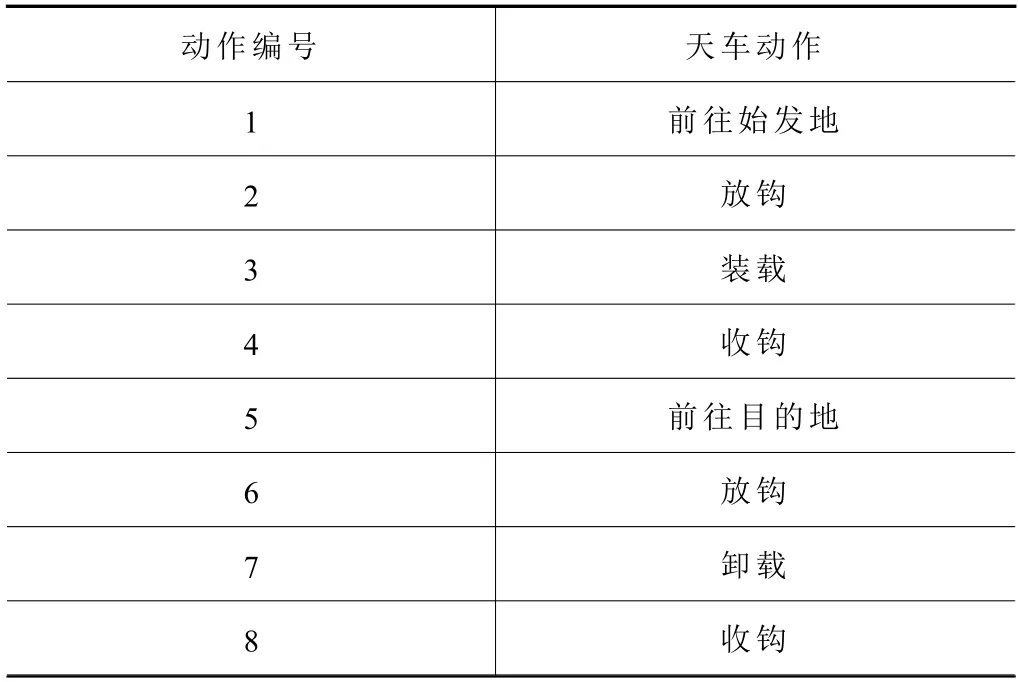
表2 天车动作表

根据天车动作，本文设计了排程表变换算子schedule_transfer、天车移动算子move、天车调度动作算子transfer、天车干涉算子collision、自适应采样时间算子change_dtime，并进一步设计了一种基于动作分解的天车解码规则。解码流程如图5 所示，具体步骤如下：

图5 基于动作分解的天车解码流程图

步骤1：将已完成选择、交叉、变异操作的染色体，通过不完全排程表变换算子schedule_transfer，使抽象的染色体变换为易于阅读的不完全排程表。不完全排程表包含工件号job、工件工序号job_pro、始发地start、目的地target、分配的天车号portal，但不包含各工件工序的开始、结束时间和天车调度任务的开始、结束时间。

步骤2：将不完全排程表作为输入，根据天车干涉发生与否分别使用天车干涉算子collision、天车调度动作算子transfer 计算并记录各个工件的加工开始时间j_starttime、结束时间j_endtime、各个天车调度任务的开始时间p_starttime、结束时间p_starttime、各个天车横坐标随时间的变化[coord_x,t]。

步骤3：根据天车间距离判断是否发生干涉。是则调用天车干涉算子collision，collision 进一步调用move；否则调用天车调度算子transfer，transfer进一步调用天车移动算子move。算子返回天车坐标、天车状态，并记录任务时间。

步骤4：使用自适应采样时间算子change_dtime 确定下一个采样时间点，以提高计算效率。

步骤5：判断是否完成全部调度任务，是则生成包含调度时间信息的完全排程表并输出，基于动作分解的天车解码完成；否则根据步骤4 更新时间，回到步骤3。

需要说明的是，天车避让使用基于优先级的避让策略，根据天车的运行状态制定优先级，如表3所示。优先级低的天车需避让优先级高的天车，当两天车优先级相同时采取轮流避让策略。

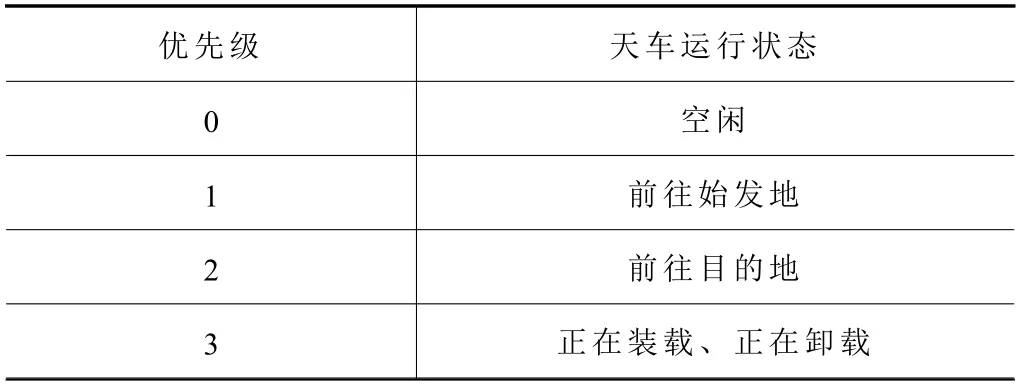
表3 天车优先级制定

表4 给出了本文所提出方法相对标准遗传算法的改进部分及作用。

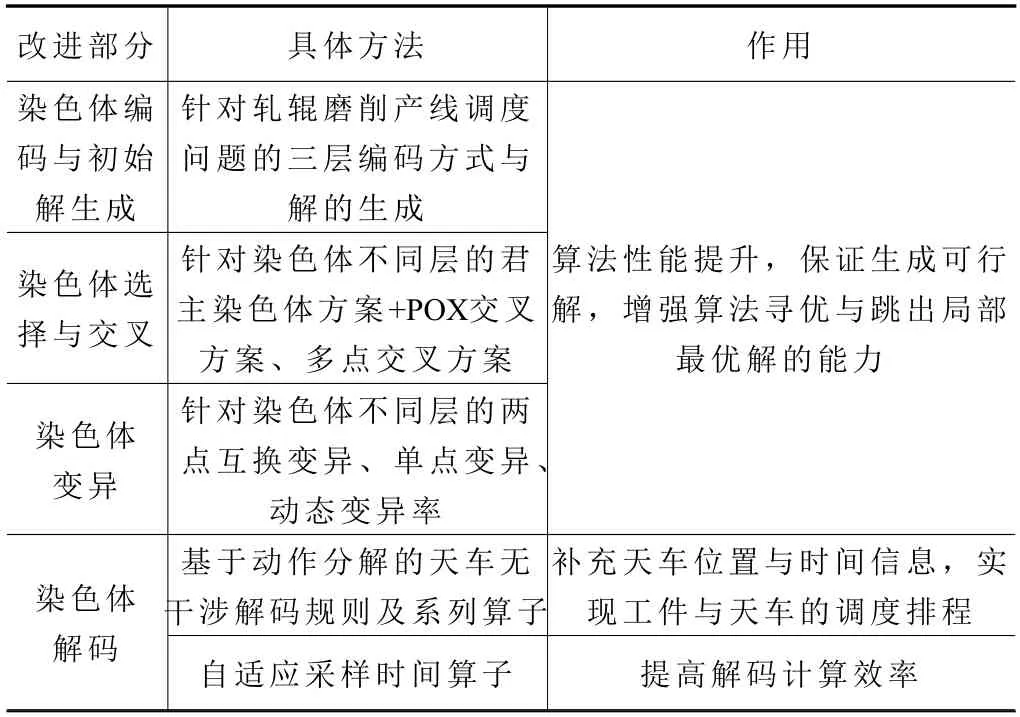
表4 本文所提出方法相对标准遗传算法的改进部分及作用

3 实例求解及结果分析

本节对改进遗传算法、原始遗传算法（经过最低限度改进以保证生成可行解的遗传算法）及某企业目前使用的排程方法的排程效果进行对比分析。轧辊磨削产线布局如图6 所示。相关环境变量设置如表5 所示，其中天车装载/卸载时间已包含对应收放钩耗时。工序流程及耗时如表6 所示，其中“-”表示该任务为调度任务而非加工任务。

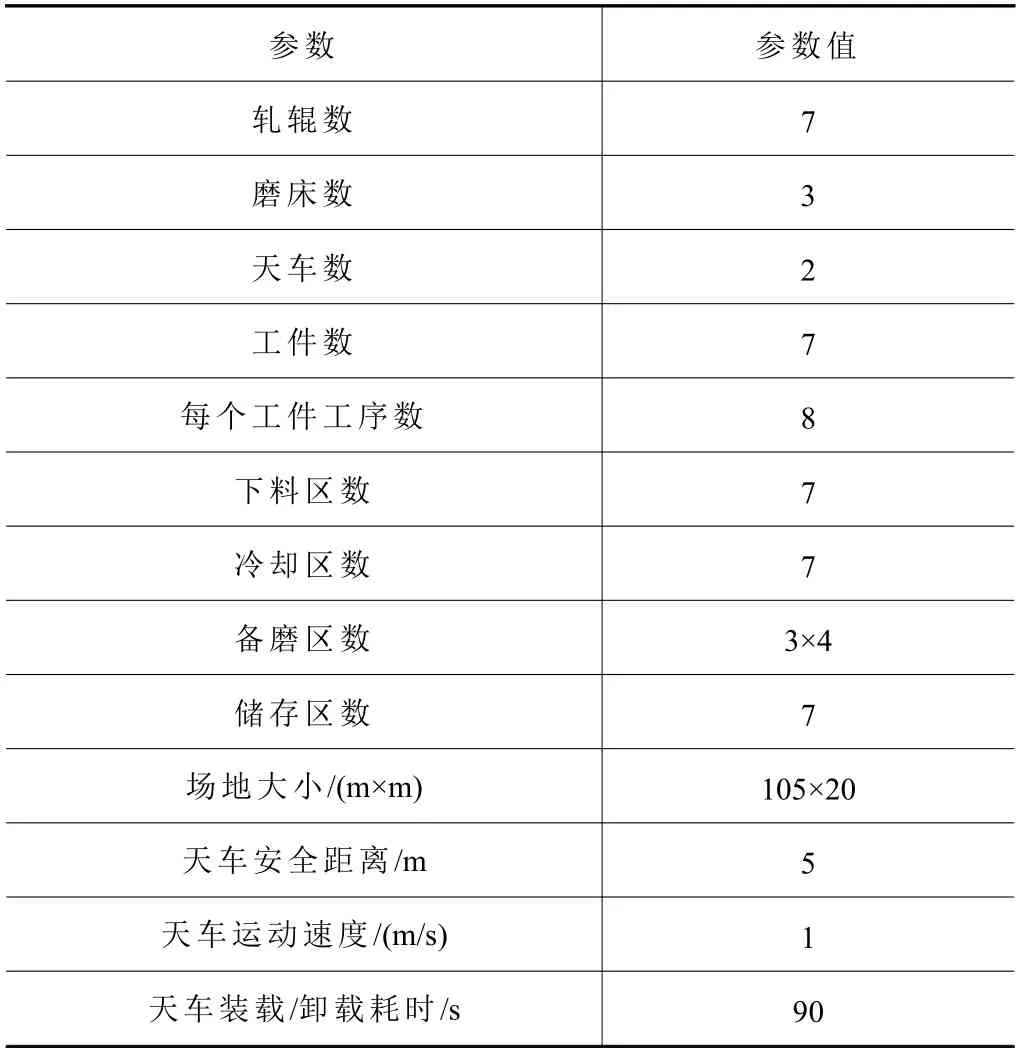
表5 车间环境变量设置

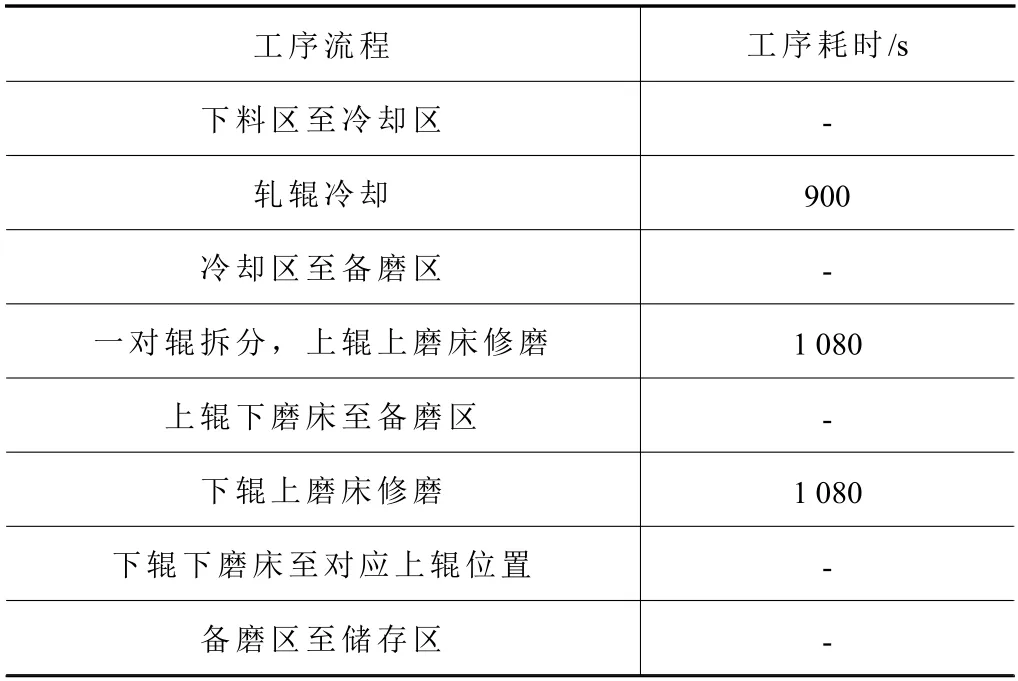
表6 工序流程及其耗时

图6 车间布局示意图

改进遗传算法及原始遗传算法的参数设置为：种群规模NP=50，最大迭代次数G=20，交叉概率Pc=0.8，初始变异概率Pm0=0.01。重复进行5 次实验。实验结果中各算法最大完工时间见表7，调度运输时长见表8。

由表7 和表8 可知，改进遗传算法生成的调度方案在最大完工时间指标上全面优于原始遗传算法，5 次实验中改进遗传算法的最差排程结果仍优于原始遗传算法的排程结果；相对于原始遗传算法，改进遗传算法的最大完工时间平均减少10.78%，调度运输耗时平均减少21.62%。此外，改进遗传算法也全面优于企业排程方法；相对于5 次实验结果完全相同的企业排程方法，改进遗传算法的最大完工时间和调度运输耗时分别平均减少了15.49%和28.08%。

表7 各算法最大完工时间

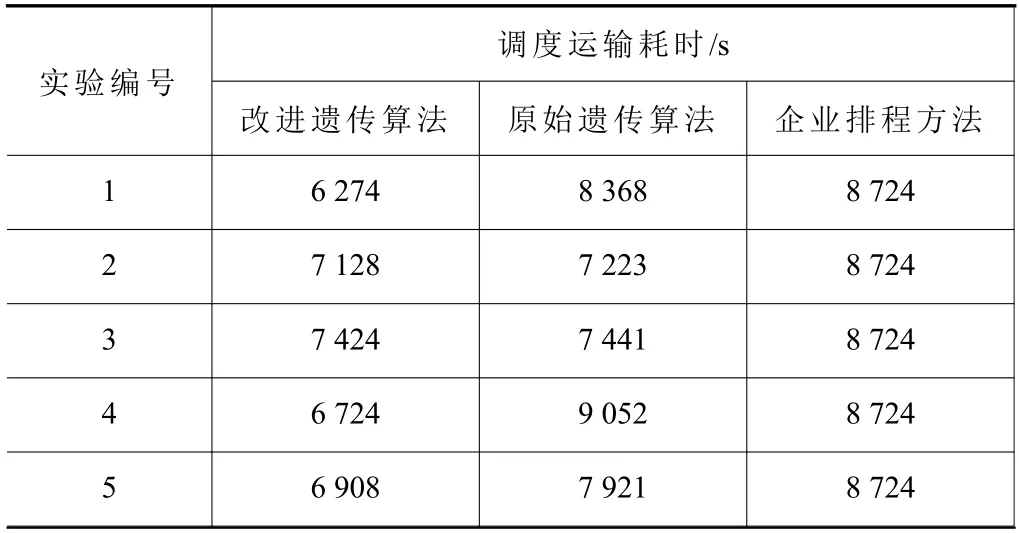
表8 各算法调度运输耗时

图7 为改进遗传算法与原始遗传算法的进化曲线图。由图可知，标准遗传算法在第2 轮迭代即找到了一局部最优解，此后趋于平缓；而改进遗传算法直至第7 轮迭代时仍保持下降趋势，从第8 轮迭代开始趋于平缓，且改进遗传算法找到的最优解要优于原始遗传算法的最优解，说明改进遗传算法的全局寻优能力与跳出局部最优解的能力要强于原始遗传算法。

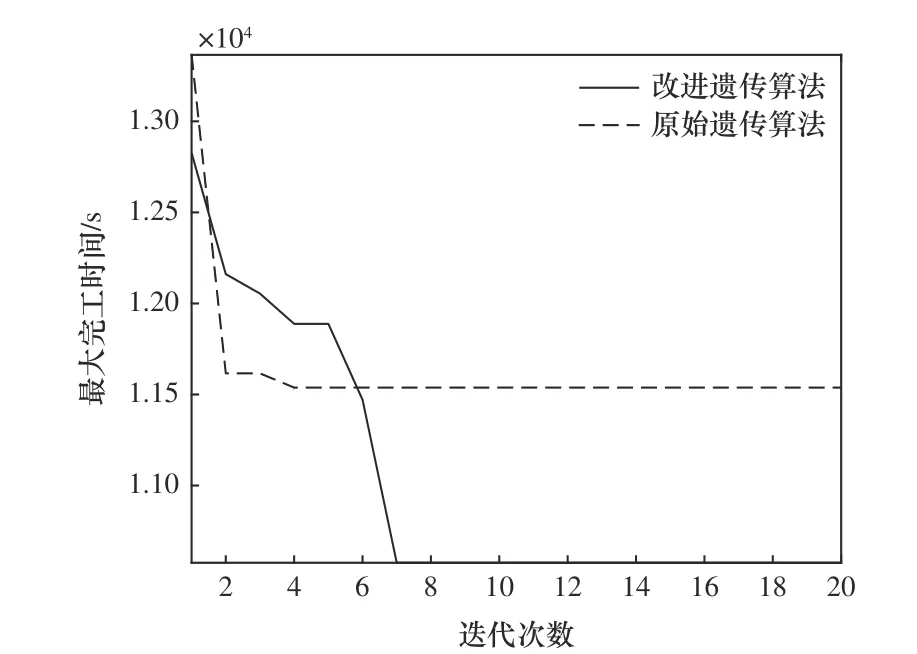
图7 改进遗传算法与原始遗传算法的进化曲线

图8 为改进遗传算法中最佳排程方案的甘特图，图中矩形无重叠部分，证明排程方案的合理性。

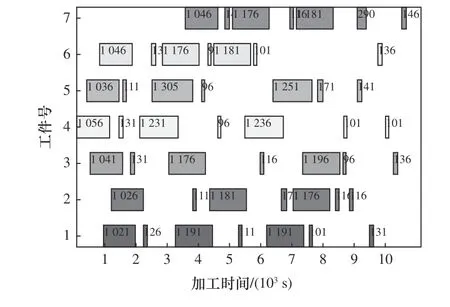
图8 改进遗传算法最佳调度方案对应甘特图

图9 为天车沿轨道方向的位移图，将图9 局部放大得图10。图中两折线分别为两天车位移随时间的变化，易知两折线斜率相同，避让操作期间两天车的运动趋势相同。设置天车间安全距离为5 m，由图可知157 s 时两天车的位移为26 m、32 m，164 s时两天车的位移为30 m、36 m，即位移差值恒为6 m，避让操作期间两天车间距始终保持恒定且大于安全距离；如不伴随，两折线距离将不断减小并最终相交，即天车发生碰撞。

图9 改进遗传算法最佳调度方案对应天车位移图

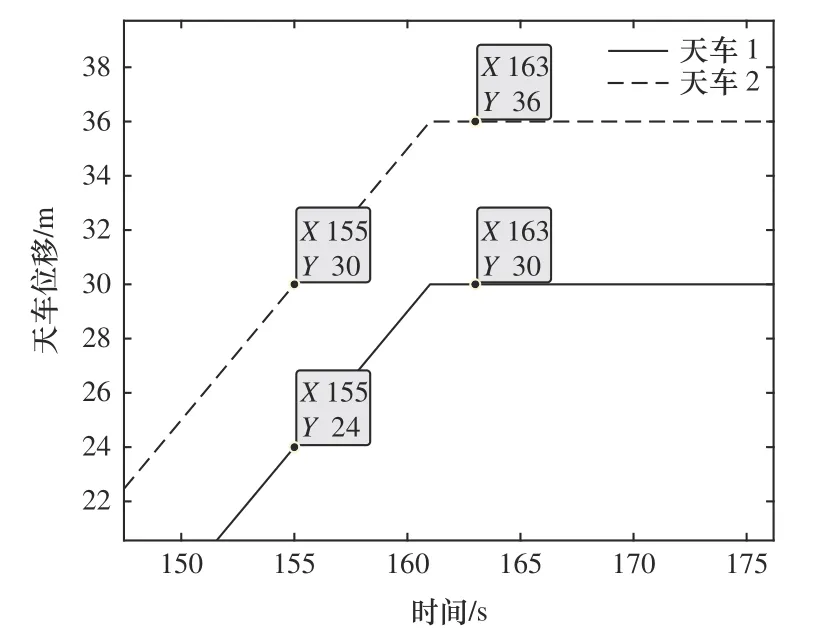
图10 两天车保持安全距离

上述结果充分证明了所提出基于改进遗传算法的智能排程方法的有效性和优越性。

4 结语

本文针对轧辊磨削产线调度问题，提出了一种基于改进遗传算法的智能排程方法。从编码、选择、交叉和变异等4 个方面对遗传算法进行了改进，设计了基于动作分解的天车解码规则及系列算子，有效解决了多天车运动干涉问题，最终实现了“工件-设备-天车”复杂时空耦合约束下的高效智能排程。验证结果显示，与原始遗传算法和企业排程方法相比，所提出智能排程方法的最大完工时间平均缩短10.78%与15.49%，调度运输耗时平均缩短21.62%与28.08%，因此，所提出的智能排程方法明显更优。相关研究成果可为提升轧辊磨削产线的调度效率与智能化水平提供核心算法支撑。