渗碳齿轮接触疲劳特性及寿命预测模型构建＊

康贺铭 邓海龙② 李明凯 李永平 陈 雨 杨 溥 于 欢

（①内蒙古工业大学机械工程学院，内蒙古 呼和浩特 010051；②内蒙古自治区先进制造技术重点实验室，内蒙古 呼和浩特 010051）

齿轮传动有传动效率高、传动比准确和功率范围大等优点，且齿轮是工业产品中不可或缺的零件，无论大到几十米重载机械，还是小到微型马达都能够见到齿轮的身影，其尺寸从几毫米到十几米不等。齿轮对机械的安全性、可靠性以及经济性起着至关重要的作用。

研究人员针对齿形、材料、表面缺陷以及工况等因素对齿轮接触疲劳的影响进行研究。基于交变赫兹接触应力并建立啮合齿轮动力学模型，可以获得齿轮工作时的接触应力分布[1-2]。基于疲劳断裂破坏的理论基础，可将疲劳裂纹分为萌生和扩展。从裂纹萌生+扩展角度，赵国伟[3]构建了萌生+扩展的寿命预测模型。从裂纹萌生角度，李智[4]虑及齿面粗糙度，构建了以萌生为主的齿轮接触疲劳寿命预测模型。从裂纹扩展角度，罗敏[5]等人探究了非金属夹杂对接触疲劳裂纹萌生及扩展的影响，并构建了以扩展为主的寿命预测模型。Chue C H[6]虑及裂纹初始特征以及载荷大小构建了裂纹扩展寿命模型。Keer L M 等[7]提出了针对接触疲劳的裂纹扩展寿命预估模型。然而，这些模型在公式推导过程中有一定的简化，且虑及因子较少。为进一步揭示超高周疲劳下齿轮接触疲劳特性，本文从裂纹扩展角度出发，基于齿轮接触疲劳失效，虑及残余应力、裂纹闭合效应、裂纹尺寸等重要因素对齿轮接触疲劳寿命的影响，建立接触疲劳寿命预测模型，对齿轮接触疲劳寿命做出更为科学的预测，为人们评估齿轮接触疲劳寿命提供新的有效方法。

1 材料及试验

1.1 材料

本文研究的齿轮材料为渗碳Cr-Ni 合金钢，化学成分如表1 所示。为使齿轮表面强度增加，对其进行气体渗碳，具体渗碳工艺流程如下：首先，将乙炔气体通入井式气体渗碳炉并保持炉温为750 ℃、炉压为1 Pa，接着将齿轮间隔5 mm 放入炉中并使炉温和炉压升至880 ℃和650 Pa 保持36 min。最后将炉温升至945 ℃保持30 min。此时齿轮的渗碳工艺完成，继续进行热处理工艺，具体流程如下：650 ℃的一次淬火，保温4 h，通过空气冷却，800 ℃的二次淬火，保温3 h 后通过油冷却，最后，150 ℃的低温回火，保温5 h 后通过空气冷却。

表1 渗碳Cr-Ni 合金钢化学成分 (%)

截取渗碳齿轮的部分组织镶嵌为金相试样，用4%酒精硝酸溶液腐蚀金相试样1 min。采用JSM-6610LV 扫描电子显微镜观测分析齿轮金相试样，得到其渗碳层和非渗碳区微观组织如图1 所示。如图1a 所示，渗碳区微观组织密度高，主要为针状马氏体和少量奥氏体，而非渗碳区域微观组织较为粗大(图1b)，且观测到有夹杂存在。

图1 渗碳齿轮微观组织

1.2 力学性能特征

基于渗碳齿轮金相试样，结合纳米压痕硬度测量仪，自试样表面向心部每间隔100 μm 进行打点测量，得到试样维氏硬度如图2 中黑色圆点所示。

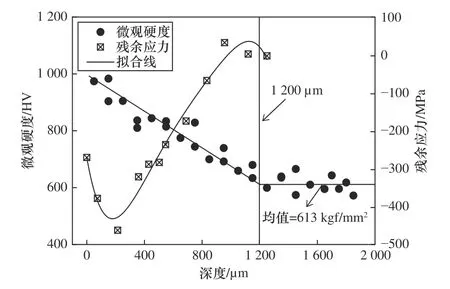
图2 渗碳齿轮微观硬度及残余应力

由图2 可知：随着深度的增加齿轮硬度呈线性递减趋势，在深度到达1 200 μm 时，维氏硬度值趋于平稳，约为613 kgf/mm2。导致该现象的原因主要是随着深度的加深，渗碳工艺的影响逐渐减小。

基于MTS809 材料测试系统对疲劳试样进行单轴力学拉伸性能试验，获得其材料的屈服强度σy为1 490 MPa，抗拉强度σb为1 780 MPa，泊松比vh为0.3，弹性模量Eh为209 GPa。

采用电解腐蚀法去除表面材料，进一步基于TEC4000 X 射线衍射系统，可得到从表面到内部的残余应力值，如图2 中空心方块所示。试样表面的残余应力为-268 MPa。当距离表面深度达到1 200 μm 左右时，残余应力消失，进一步证明了试样渗碳层深度约为1 200 μm。基于多项式拟合可以得到残余应力（σr）与深度（z）的关系

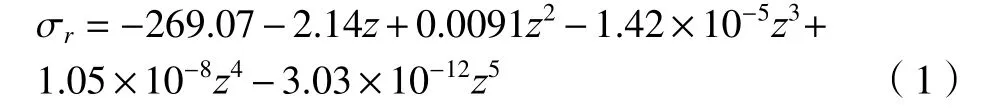
1.3 试验

基于齿轮接触疲劳试验机开展齿轮接触疲劳试验。为获得其疲劳性能，设置试验机转速为2 000 r/min，并在不同扭矩下开展齿轮接触疲劳试验，疲劳试验机如图3 所示。

图3 齿轮接触疲劳试验机

2 试验结果

2.1 接触应力计算

主/从动齿轮参数如表2 所示。基于Hertz 理论：弹性体材料特性为各向同性材料；接触区域内的接触应力不应超过金属材料弹性屈服极限；接触面积应远小于接触物总表面积；有效压力应垂直于接触物体的外表面；接触表面绝对光滑，不考虑润滑油及动摩擦系数等影响[8]。当齿宽为a，分度圆半径分别为r1、r2的齿轮对啮合时（图4），可视为等效半径分别为ρ1、ρ2，长为a的两个圆柱体接触（图5）。

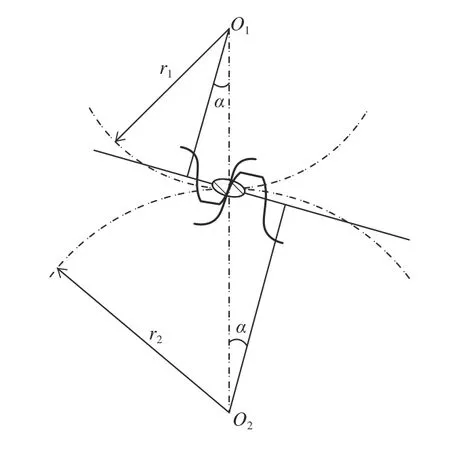
图4 齿轮对在啮合点处接触的示意图

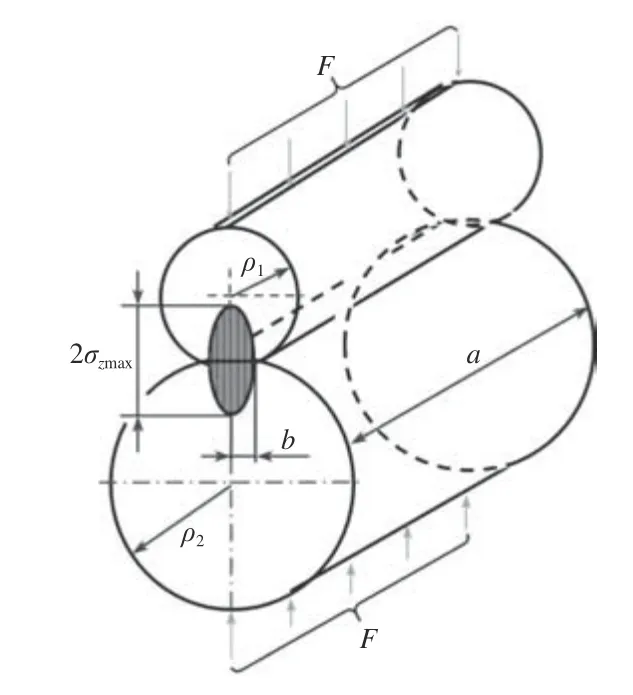
图5 两圆柱接触示意图

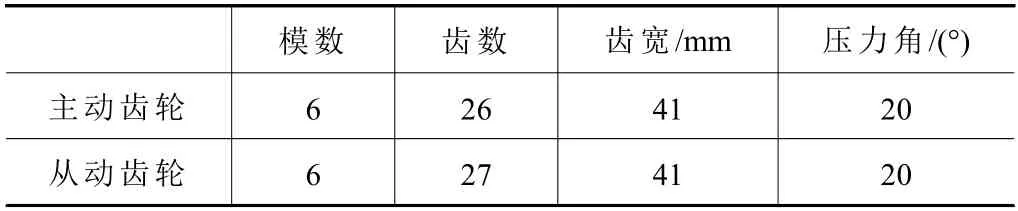
表2 齿轮参数

式中：d1为齿轮1 的节圆半径；d2为齿轮2 的节圆半径；α为齿轮压力角。

如图5 所示，当两圆柱弹性体接触时，会形成宽度为2b的矩形接触面。

接触应力大小在宽度2b方向上呈抛物线分布。因此，最大名义接触应力σzmax可表示为

式中：F为施加载荷。

基于局部应变分析可知，接触宽度b可表示为

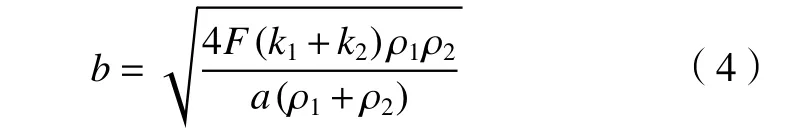
式中：k1、k2为模型常数；结合式（2）～（4），可得接触应力计算公式

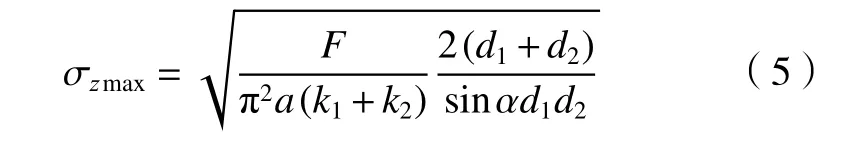
在齿轮转速为2 000 r/min，齿轮扭矩为2 000 N·m、3 000 N·m、3 500 N·m 和4 500 N·m 时，结合式（5），可得到本文数据点的接触应力分别为1 320 MPa、1 620 MPa、1 750 MPa 和1 985 MPa。

2.2 S-N 曲线

齿轮疲劳试验结束后，其接触疲劳结果如图6所示。由图可知，齿轮接触疲劳寿命在106至108循环周次内呈现持续下降的S-N特性，并不存在传统的107循环周次下的疲劳极限。基于极大似然数法及Basquin 模型拟合得到齿轮接触疲劳S-N曲线，如图6 所示。由图可知，齿轮接触疲劳S-N曲线的拟合程度较高。若定义齿轮接触疲劳极限为108循环周次接触疲劳寿命处的疲劳强度，通过拟合曲线可知，该齿轮的疲劳极限约为1 240 MPa。

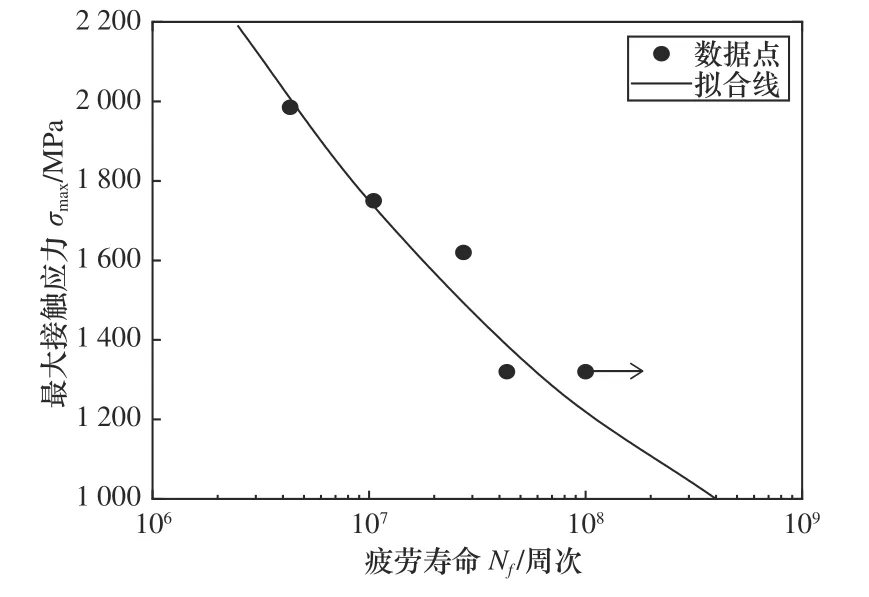
图6 渗碳齿轮S-N 曲线

2.3 点蚀形貌

设置齿轮试验转速以及扭矩分别为2 000 r/min以及2 000 N·m，同一齿轮加载至出现明显缺陷特征后将齿轮卸下拍摄其同一齿面形貌，得到同一齿轮齿面不同循环周次下的形貌如图7 所示。

图7 试验过程

通过实验研究发现，齿轮在加载至2.8×107周次时，其齿面可观测到明显的磨损区域，进而随着循环次数的增加，形成明显的点蚀现象(图7c），并且当点蚀面积达到齿轮工作表面积4%时，判定其失效[9]。

3 接触疲劳寿命预测模型

当齿轮受循环载荷作用时，在距齿面深H处会形成裂纹长度为a0的初始微裂纹，基于试验结论可知[10]：裂纹产生的位置主要取决于材料的硬度以及齿轮受到的最大剪应力。当应力状态及最大剪应力一定时，裂纹扩展速率在低硬度下比在高硬度下扩展速率快。随着裂纹的发展，裂纹尖端应力强度因子范围ΔK会发生变化，为了计算裂纹扩展速率，需要建立虑及裂纹长度变化的应力强度因子值计算方法。当裂纹扩展过程中的应力分布能够确定时，Hearle 和Johnson 构建了随裂纹扩展的Ⅱ型裂纹尖端应力强度因子计算公式[11]，表达式为

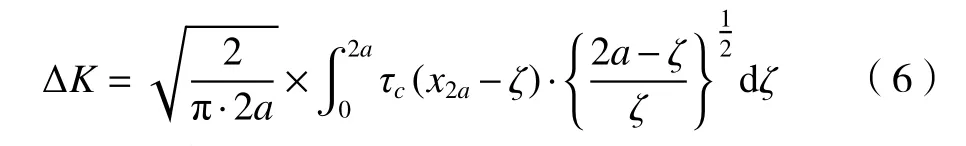
其中：τc为净切应力；a为半裂纹长度；ζ为裂纹扩展增量；τeqv.为等效切应力。

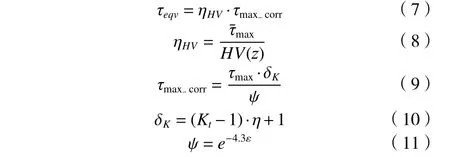
其中 ：τmax_corr为修正最大切应力；ηHV为硬度因子；τmax为应力区内最大应力；ψ虑及孔洞的影响，其承载面面积会产生变化；ε为孔洞系数，其值为0.11；Kt为孔洞形状系数，其值为2；δK为缺口效应修正系数；η为基体组织修正系数，取值为0.7；HV(z)为深度z处的硬度，其关系如图8 所示。

图8 裂纹扩展示意图

虑及裂纹闭合效应，将式（6）改写为

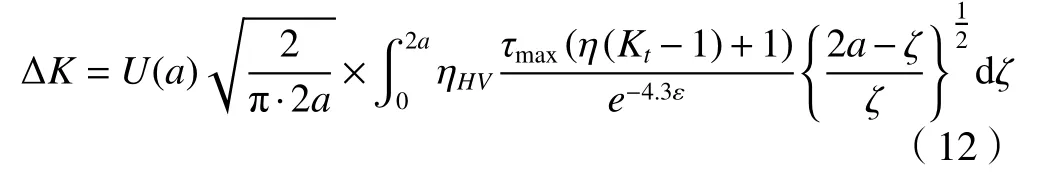
U(a)为裂纹闭合效应系数，其表达式如下[12]。

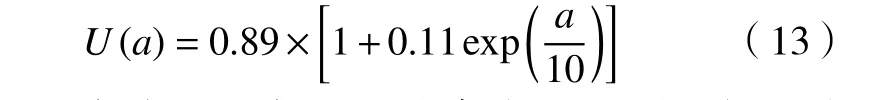
虑及因渗碳工艺产生的残余应力对裂纹扩展寿命的影响，齿轮次表面中最大剪切应力的计算公式可表示为

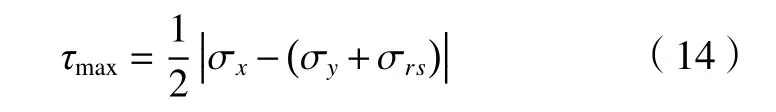
式中：σx为齿轮次表面内切向应力；σy为齿轮次表面内法向应力。其表达式分别为

式中：yi为裂纹尖端距齿轮表面的深度；r为半齿轮接触面宽度。

基于Paris 公式、虑及齿轮硬度影响，裂纹扩展寿命模型可表示为[13]

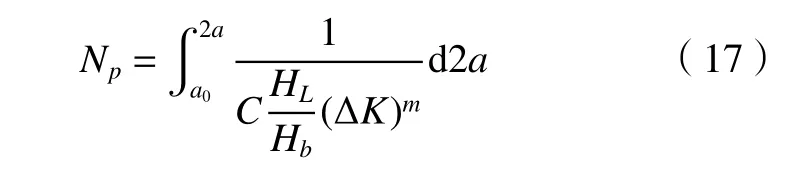
式中：a0为初始裂纹长度；Hb为齿轮整体硬度；HL为齿轮局部硬度；C为裂纹扩展速率的系数；m为裂纹扩展速率的指数。

初始裂纹长度可表达为

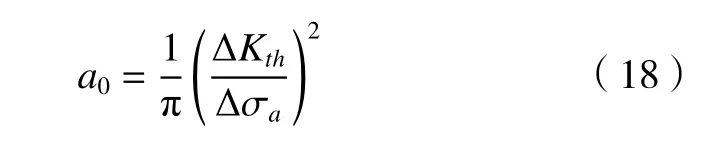
其中：ΔKth为应力强度因子门槛值，其值通过经验公式得到[14]

基于式（14），虑及齿轮局部与整体硬度、残余应力、裂纹闭合效应和裂纹长度对裂纹扩展寿命的影响，式（17）在[a0,ac]进行积分得到齿轮裂纹扩展寿命预测模型

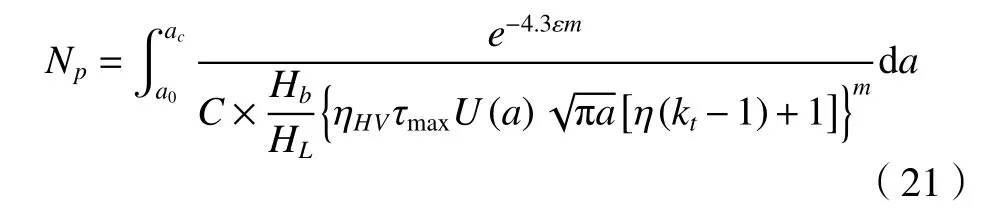
裂纹扩展寿命预测模型的预测寿命与试验寿命的对比结果如表3 所示。由表3 可知：所构建的裂纹扩展寿命预测模型预测结果精度较高，所有试验点预测均在2 倍因子内，其预测结果是可接受的。

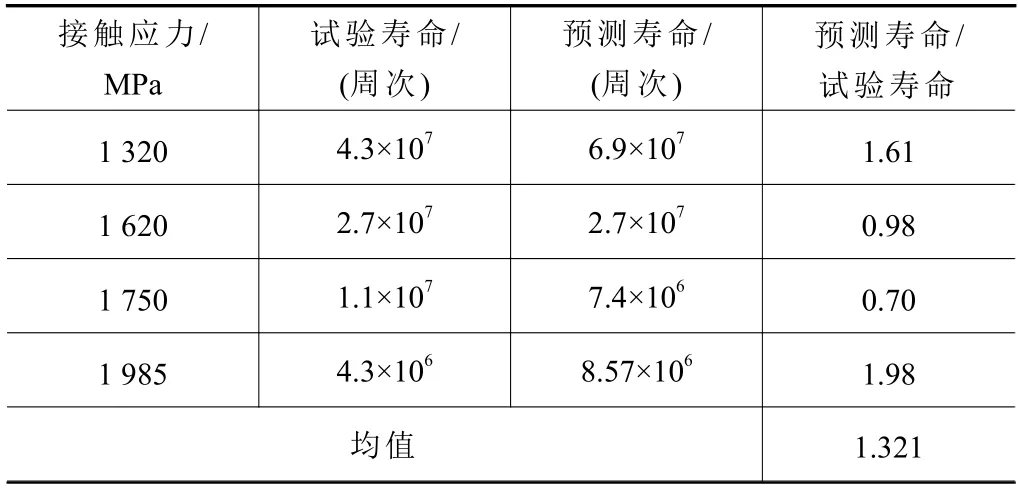
表3 模型预测寿命与试验寿命对比

4 结语

（1）通过齿轮接触疲劳试验，并结合赫兹接触理论获得S-N曲线及齿轮点蚀形貌。基于齿轮SN曲线，当定义齿轮接触疲劳极限为108循环周次的疲劳寿命处的疲劳强度时，其值约为1 240 MPa。

（2）结合线弹性断裂力学和裂纹扩展速率，虑及材料硬度、闭合效应及裂纹长度等因素，构建渗碳齿轮裂纹扩展寿命预测模型。

（3）所构建的齿轮接触疲劳寿命预测模型预测精度较高，其误差在2 倍以内，为人们预测齿轮接触疲劳寿命提供了有效的方法。