2 300 m超大跨度扁平钢箱梁悬索桥颤振稳定性优化研究

黄 林， 廖海黎， 王 骑， 李 强， 李志国

(1.西南交通大学 桥梁工程系，成都 610031； 2.风工程四川省重点实验室，成都 610031)

随着我国社会经济的发展以及城市群之间的联系越加紧密，国家对海洋、河道及沿岸生态保护区域范围逐渐扩大，我国沿海和沿江城市群已出现了对超大跨度桥梁的建设需求，主要以河道宽敞、临海且经济高度发达的江浙沪超大城市群和粤港澳大湾区为代表。

张皋过江通道地处长江三角城市群的中心，处于重点规划的锡常泰、(沪)苏通都市圈和沿江经济发展带的结合处，位于江阴大桥下游约28 km处，苏通大桥上游约57 km处，在张家港和如皋境内跨越长江。其中张皋过江通道南航道桥(主江航道桥)采用主跨2 300 m的悬索桥设计方案，为当前世界在建的最大跨度悬索桥。

目前世界上已建成或已完成设计并在建的1 600 m以上跨度的悬索桥共计7座(如表1所示)，其中整体钢箱梁由于具有优良的抗风稳定性和涡激振动特性，自从1950年代在英国Severn桥成功应用于工程实践之后，被广泛应用于大跨度悬索桥，桁梁作为悬索桥的传统主梁形式，由于抗扭刚度较大，一般具有优良的颤振稳定性，并没有涡激振动现象，但存在横向风载大和横向位移大等不足。分体钢箱梁具有优异的颤振稳定性，但涡激振动控制方面容易成为抗风设计的难点[1-4]。

张皋过江通道南航道桥主梁采用整体扁平钢箱梁设计，但经过以往在虎门二桥和伶仃洋大桥抗风设计中所获得的一个重要认识[5]，在沿海高风速地区建造1 700 m以上跨度的悬索桥，传统整体钢箱梁的颤振稳定性已很难满足设计要求，需要开发气动特性更为优良的断面形式或气动控制技术。

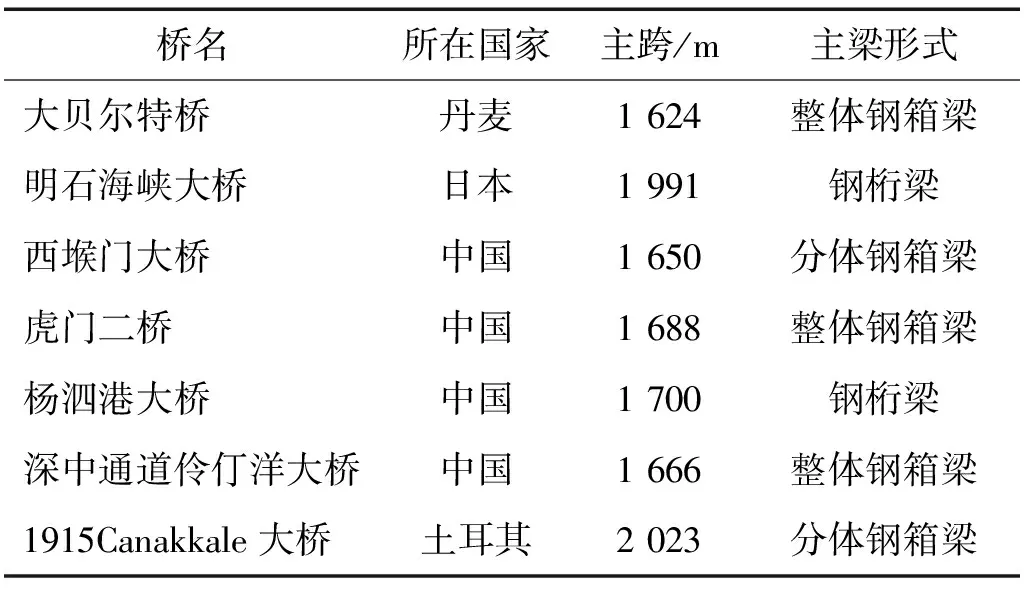
表1 世界1 600 m以上跨度悬索桥

就如何改善整体箱梁断面的颤振稳定性，国内外学者已开展了一系列相关研究。Katsuchi等[6]通过对日本明石海峡大桥的颤振性能改善研究发现，设置上中央稳定板可以有效提高桥梁断面的颤振临界风速。杨詠昕等[7]通过节段模型风洞试验肯定了中央稳定板的颤振控制作用，并对机理进行了研究。Larsen[8]就桥面附属结构对大跨度整体钢箱梁悬索桥颤振临界风速的影响进行了研究。Wilde等[9]研究了主动翼板控制系统在改善桥梁断面颤振性能中的作用，但从可靠性考虑，相比被动控制措施，主动控制措施存在能量供给以及耐久性不足等问题。张宏杰等[10]通过对中央稳定板、中央开槽与加装悬臂水平分离板等一系列气动措施的颤振控制效果进行研究发现，水平分离板对扁平箱梁的颤振性能改善效果良好，尤其在正风攻角下提高效果更加显著。Wang等[11-12]通过一系列风洞对比发现，将扁平箱梁斜腹板的倾角控制在16°以内有利于提高桥梁的颤振临界风速。夏锦林等[13]在研究单侧稳定板对箱梁颤振控制作用的基础上，对不同高度组合的上、下中央稳定板的控制效果进行了深入研究，发现同时设置上、下中央稳定板提升效果更加显著。张亮亮等[14]通过数值模拟与风洞试验对宽体式扁平钢箱梁颤振特性进行了分析，研究结果表明桥面附属结构的位置对主梁颤振稳定性的影响极大，设计时应慎重选择布置位置。赵林等通过对深中通道伶仃洋大桥主梁断面的结构选型，研究了不同梁高的扁平钢箱梁颤振稳定性之间差异。李加武等[15]发现在不过多降低检修道栏杆透风率的情况下对检修道栏杆进行适当的间隔封闭可以在一定程度上提高扁平箱梁断面的颤振临界风速。

从结构设计方面出发，张皋过江通道南航道桥的颤振控制存在两大难点：一是桥梁主跨极大，张皋过江通道南航道桥是我国首座跨度超过2 000 m的悬索桥，也是世界上第一座采用整体钢箱梁的主跨2 000 m级超大跨度悬索桥，结构柔度的显著增大将导致该桥对风的作用极为敏感度；二是主梁断面宽度大，张皋过江通道南航道桥的主梁宽度达到51.7 m，主梁在顺风方向特征尺寸较大。

对于张皋过江通道南航道桥，需要对以往研究所发现的有效颤振控制措施的有效性进行进一步研究与验证。本文从抗风设计的角度出发，在1∶50比例尺下开展了一系列节段模型风洞试验，对张皋过江通道南航道桥主梁的颤振稳定性进行了研究，在对比了上中央稳定板、下中央稳定板、水平稳定板、斜导流板以及改变人行道板倾角等气动措施颤振控制作用的基础上，提出了一种可满足颤振设计要求的组合气动措施，并通过全桥气弹模型风洞试验对该措施的有效性进行了检验。

1 工程背景

本文以张皋过江通道南航道桥为工程背景，该桥为一座主跨为2 300 m的超大跨度公路悬索桥，大桥全长4.18 km，包括主桥、南边跨以及南北引桥，跨径布置为660+2 300+717+503=4 180 m，桥塔高350 m，主跨矢跨比为1/6.6，桥型布置如图1所示。

图1 张皋过江通道南航道桥桥型布置(m)Fig.1 Layout of the Zhanggao south channel bridge(m)

主梁采用双向八车道的扁平钢箱梁，梁宽51.7 m，梁高4.5 m，宽高比达到11.5，桥面板厚度设计为16 mm，两侧设悬挑2.1 m宽人行道板，具体如图2所示。

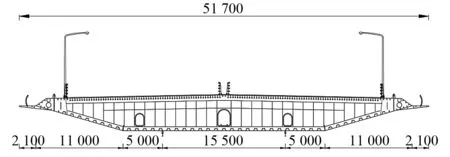
图2 张皋过江通道南航道桥主梁示意图(mm)Fig.2 Diagram of the Zhanggao south channel bridge main girder(mm)

为了获得张皋过江通道的合理设计风参数，收集了张皋过江通道桥位附近气象台站风速数据，并采用气象统计学中Gumbel Type I极值分布理论进行分析，计算得到了主要气象站的基本风速，同时从JTG/T 3360-01—2018《公路桥梁抗风设计规范》[16]中，查知桥位所属南通地区的海拔及基本风速，具体数据如表2所示。

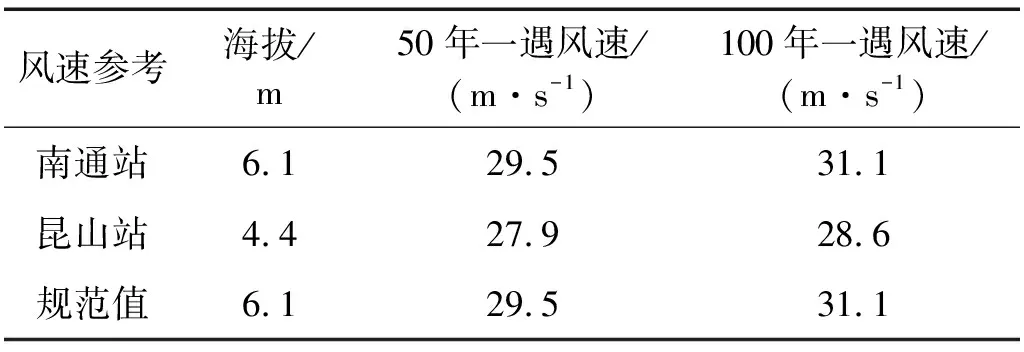
表2 桥位附近主要气象台站基本风速

根据表2中数据，可偏于安全地将桥位处基准风速取为规范建议值，考虑百年一遇最大风速31.1 m/s作为基本风速。通过该基本风速，按JTG/T 3360-01—2018《公路桥梁抗风设计规范》计算得到该桥在0°，±3°风攻角下的成桥态颤振检验风速为62.8 m/s。

2 节段模型风洞试验

2.1 试验参数

节段模型颤振试验在西南交通大学XNJD-1风洞第二试验段进行，该试验段截面尺寸为2.4 m(宽)×2.0 m(高)×16.0 m(长)。基于主梁及风洞断面尺寸，为满足风洞试验要求，试验模型缩尺比选用1∶50，模型长度、宽度和高度分别为2.095 m，1.034 m和0.090 m，阻塞度小于5%。主梁上表面进行蒙皮，栏杆与检修车轨道采用ABS塑料板制作，其中栏杆确保了透风率相似。节段模型通过8根拉伸弹簧悬挂在风洞中以确保模型可以发生竖弯和扭转振动，试验模型如图3所示，试验动力参数如表3所示。

图3 节段模型Fig.3 Section model

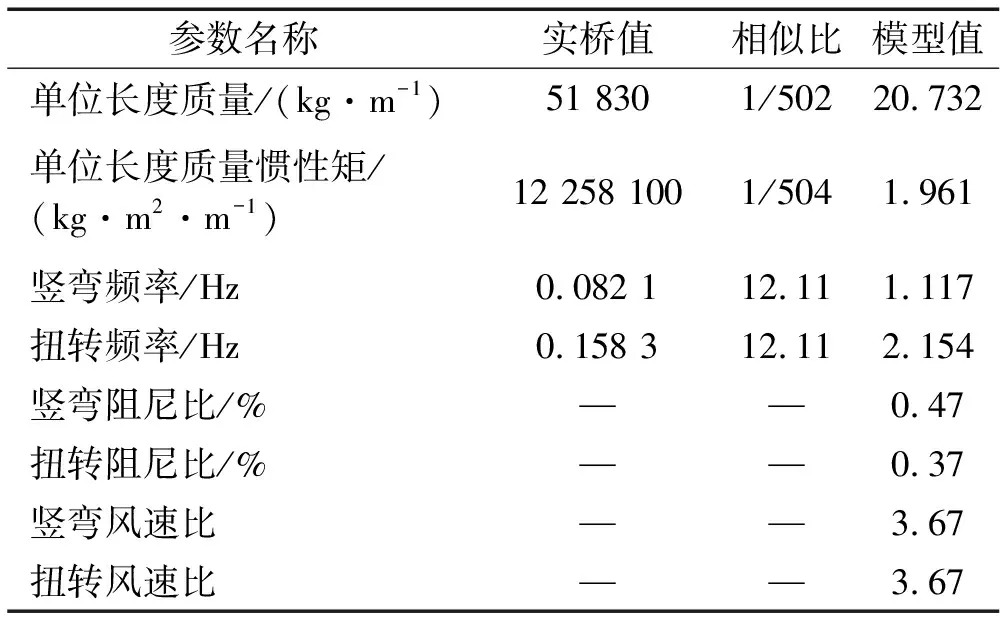
表3 节段模型试验参数

2.2 试验工况

节段模型颤振试验在0°与±3°攻角的均匀流场中完成，首先对原设计断面(YSDM)开展颤振试验，并通过设置上中央稳定板、下中央稳定板、水平稳定板、斜导流板以及改变人行道板倾角等一系列气动措施用以改善主梁的颤振稳定性，具体试验工况如表4所示(表中数据均为实桥数据)。

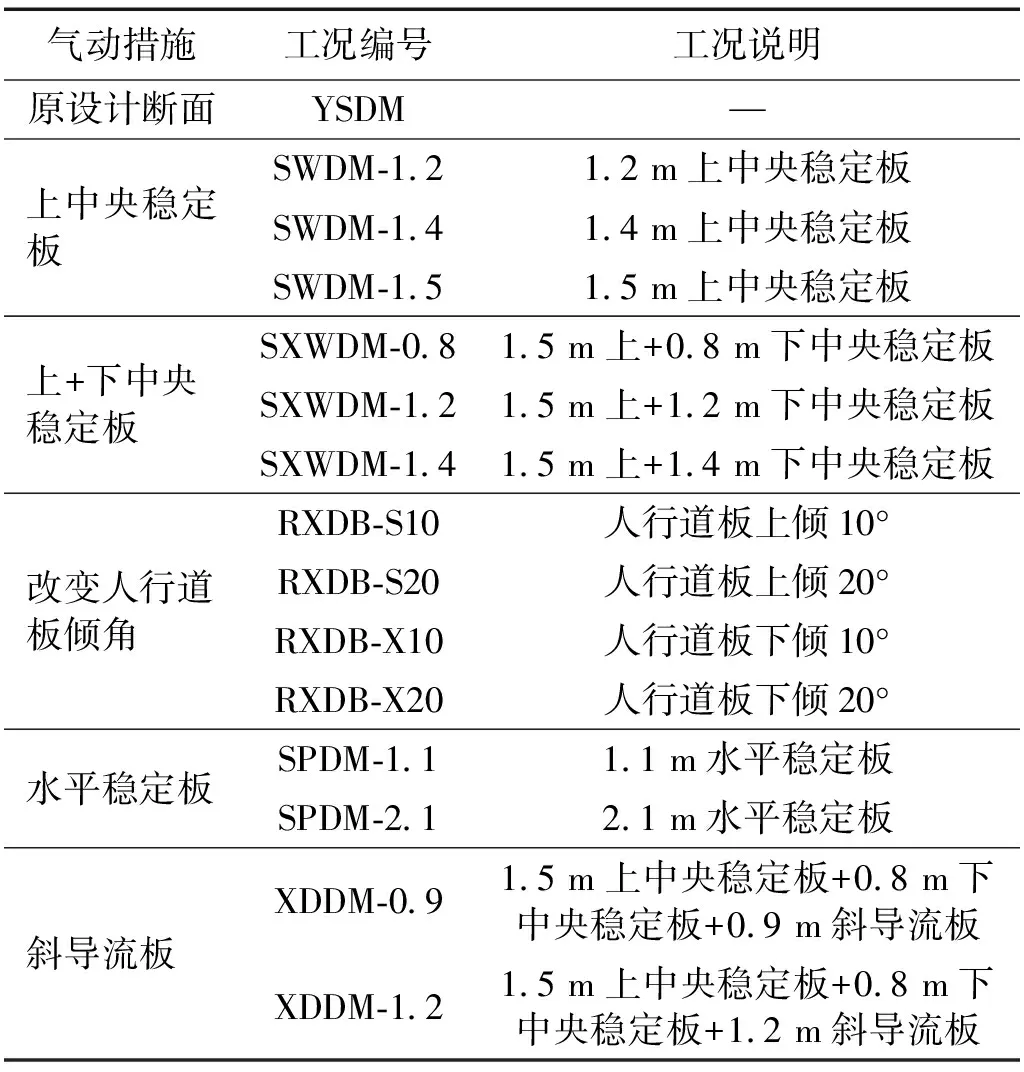
表4 试验工况说明

2.3 原设计断面颤振临界风速

通过节段模型风洞试验得到0°与±3°风攻角下原设计断面颤振临界风速如表5所示(表中数据均已换算至实桥)，可以发现该桥原设计断面在0°与±3°攻角下的颤振临界风速均明显低于颤振检验风速。

表5 原设计断面颤振临界风速

试验结果表明，该桥原设计主梁存在颤振稳定性严重不足的情况，需要设置相应措施用以改善断面的颤振性能。

3 气动措施颤振优化性能比较

3.1 上中央稳定板

参考已有文献的研究成果表明，设置上中央稳定板有利于提高扁平箱梁断面的颤振稳定性，本文分别采用三种高度(1.2 m，1.4 m与1.5 m)的上中央稳定板(措施具体细节如图4所示)，通过1∶50节段模型风洞试验测试了0°与±3°风攻角下上中央稳定板对该桥主梁颤振临界风速的影响。

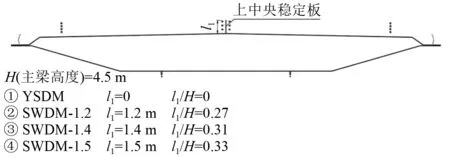
图4 SWDM工况断面示意图Fig.4 Diagram of SWDM section

各工况下主梁颤振临界风速如图5所示(图5中数据均已换算至实桥)，可以发现3种高度的上中央稳定板均能有效提高断面的颤振临界风速，但不同攻角下断面颤振临界风速随着上中央稳定板高度的变化规律并不相同。在0°与+3°攻角下，断面颤振临界风速与上中央稳定板的高度始终是正相关(l1/H≤0.33)。但在-3°风攻角下，上中央稳定板存在一个明显的最优高度区域，较原设计断面，0.27H高的上中央稳定板仅能将断面颤振临界风速提高1.2 m/s，但仅将上中央稳定板高度提高0.2 m～0.31H高后，较原设计断面，断面颤振临界风速可提升3.3 m/s，但随着稳定板高度增加至0.33H，断面临界风速反而下降，在-3°攻角下，断面颤振临界风速随着稳定板高度的增加先增大后减小，最优高度在0.31H附近。

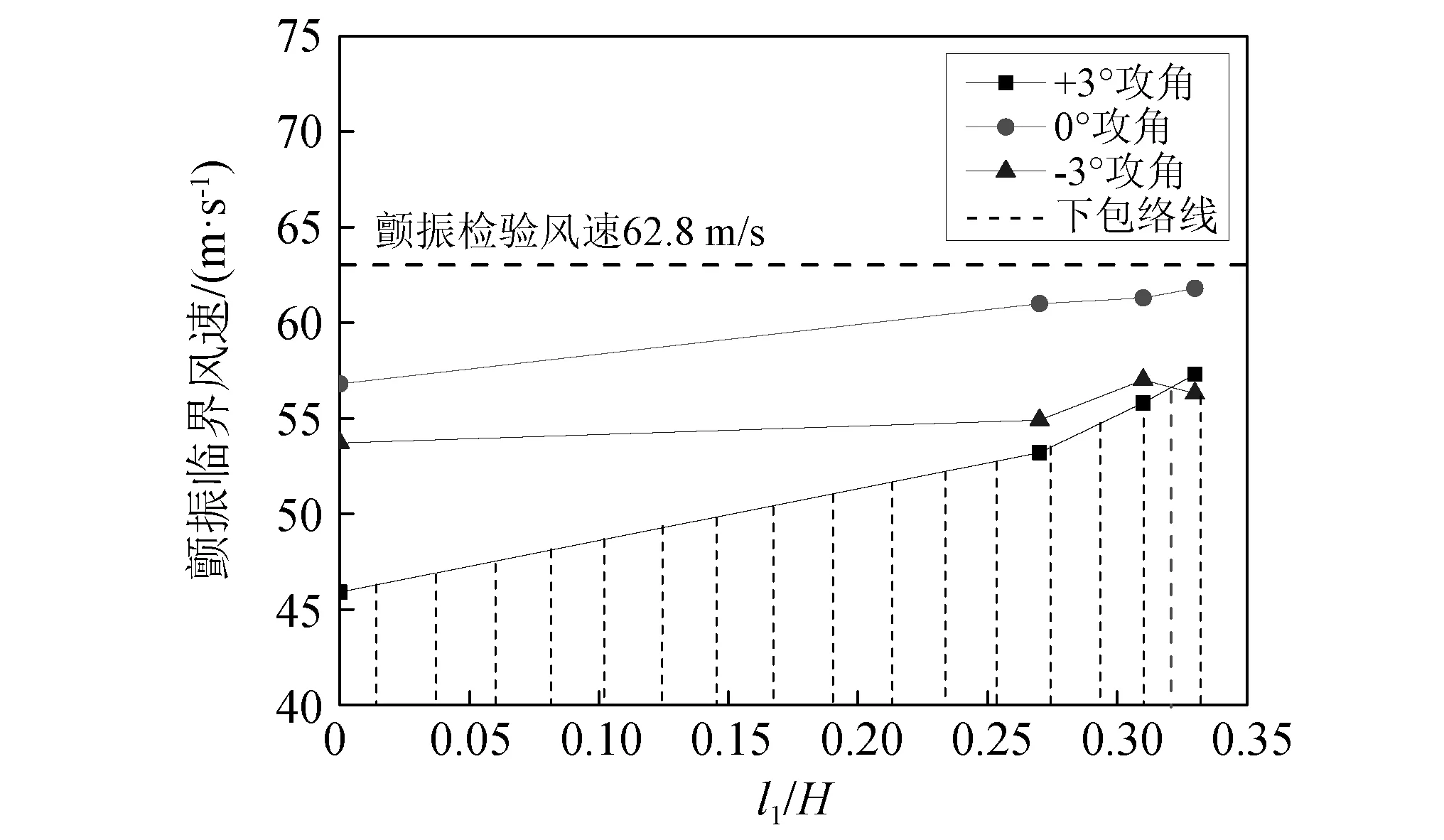
图5 SWDM工况颤振临界风速Fig.5 Flutter critical wind speed of SWDM section

通过图5中的颤振临界风速下包络线对断面的综合颤振稳定性进行评估，可以发现单独设置上中央稳定板时，0°攻角在所有高度都不起控制作用。当稳定板高度较低时，+3°攻角为最不利攻角，当稳定板高度超过最优高度点时，-3°攻角为最不利工况对断面颤振稳定性起控制作用。上中央稳定板最优高度应在0.31H～0.33H。

在本文SWDM试验工况中，1.5 m(0.33H)上中央稳定板的优化性能最佳，能将原设计断面最低颤振临界风速(45.9 m/s)提高至56.3 m/s，提高率22.7%。

3.2 上、下组合中央稳定板

在SWDM试验工况中颤振性能优化效果最佳的1.5 m(0.33H)上中央稳定板基础上设置下中央稳定板(高度范围0.18H～0.31H)，措施具体细节如图6所示，在此基础上测试了0°与±3°风攻角下上、下组合中央稳定板对该断面颤振稳定性的影响，各工况下主梁颤振临界风速如图7所示。

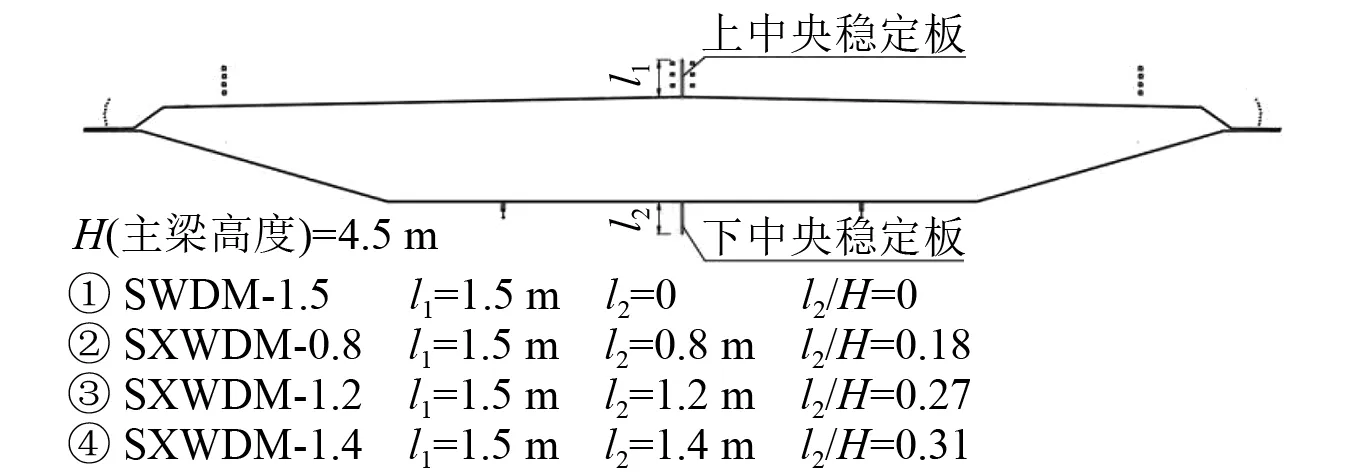
图6 SXWDM工况断面示意图Fig.6 Diagram of SXWDM section

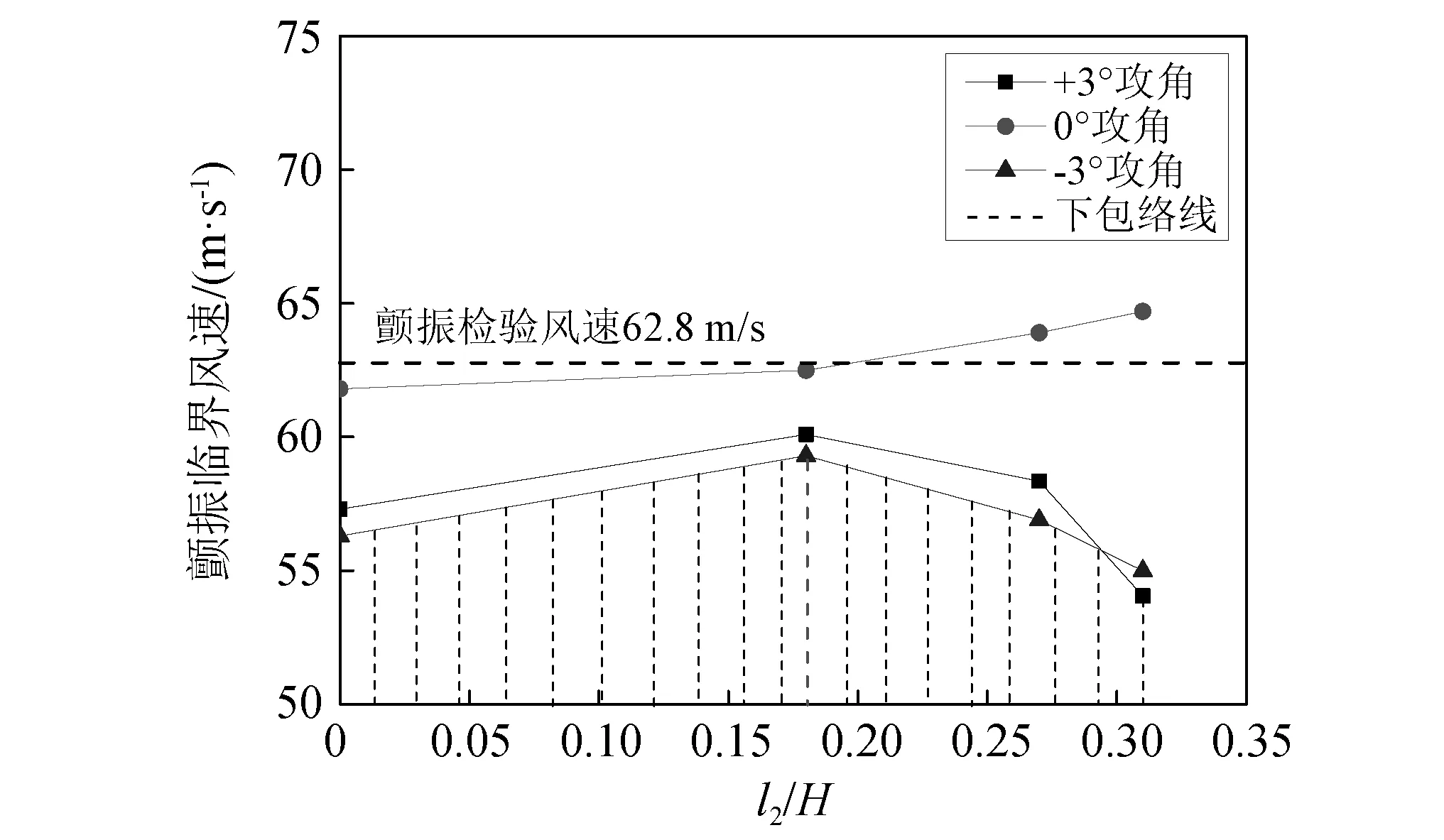
图7 SXWDM工况颤振临界风速Fig.7 Flutter critical wind speed of SXWDM section

从图6可以发现，0°风攻角下，下中央稳定板能够与上中央稳定板的颤振性能优化作用正相加，进一步提高SWDM-1.5工况断面的颤振临界风速，且提升作用与下中央稳定板的高度始终是正相关(l2/H≤0.31)。但在±3°攻角下，断面的颤振临界风速均随着下中央稳定板高度的增加先增大后减小，最优高度在0.18H，当高度超过0.27H后，下中央稳定板甚至会降低上中央稳定板的优化作用。

通过图7中的颤振临界风速下包络线对断面的综合颤振稳定性进行评估，可以发现在固定高度0.33H上中央稳定板的基础上组合设置下中央稳定板后，对断面颤振稳定性起控制作用的主要是-3°攻角，当下中央稳定板高度在0.18H时优化效果达到最佳。

在本文SXWDM试验工况中，将1.5 m(0.33H)上中央稳定板与0.8 m(0.18H)下中央稳定板相组合对断面颤振稳定性优化效果最佳，能将原设计断面最低颤振临界风速(45.9 m/s)提高至59.3 m/s，提高率29.2%，较单独设置1.5 m上中央稳定板多提高了6.5%。

3.3 人行道板倾角

人行道板位于该扁平箱梁的最外侧，由于经过桥梁断面的气流首先流经该处，因此人行道板处的变化可能会对断面的颤振稳定性产生较大影响。本文通过1∶50节段模型风洞试验测试了-3°风攻角下人行道板角度变化对断面颤振临界风速所产生的影响，RXDB试验工况中共设计了4种倾角的人行道板，分别为+10°，+20°倾角(上翘)，以及-10°，-20°倾角(下倾)，措施具体细节如图8所示。

图8 RXDB工况断面示意图Fig.8 Diagram of RXDB section

各工况下主梁颤振临界风速如图9所示，可以发现人行道板倾角处于0°(YSDM)时，断面的颤振稳定性最佳，人行道板倾角的改变均会导致-3°风攻角下断面颤振临界风速的降低，其中人行道板上翘(正倾角)时的降低作用要显著高于人行道板下倾(负倾角)时。RXDB试验工况中当人行道板处于+20°倾角时断面颤振临界风速最低，较原设计断面，颤振临界风速降低30%。

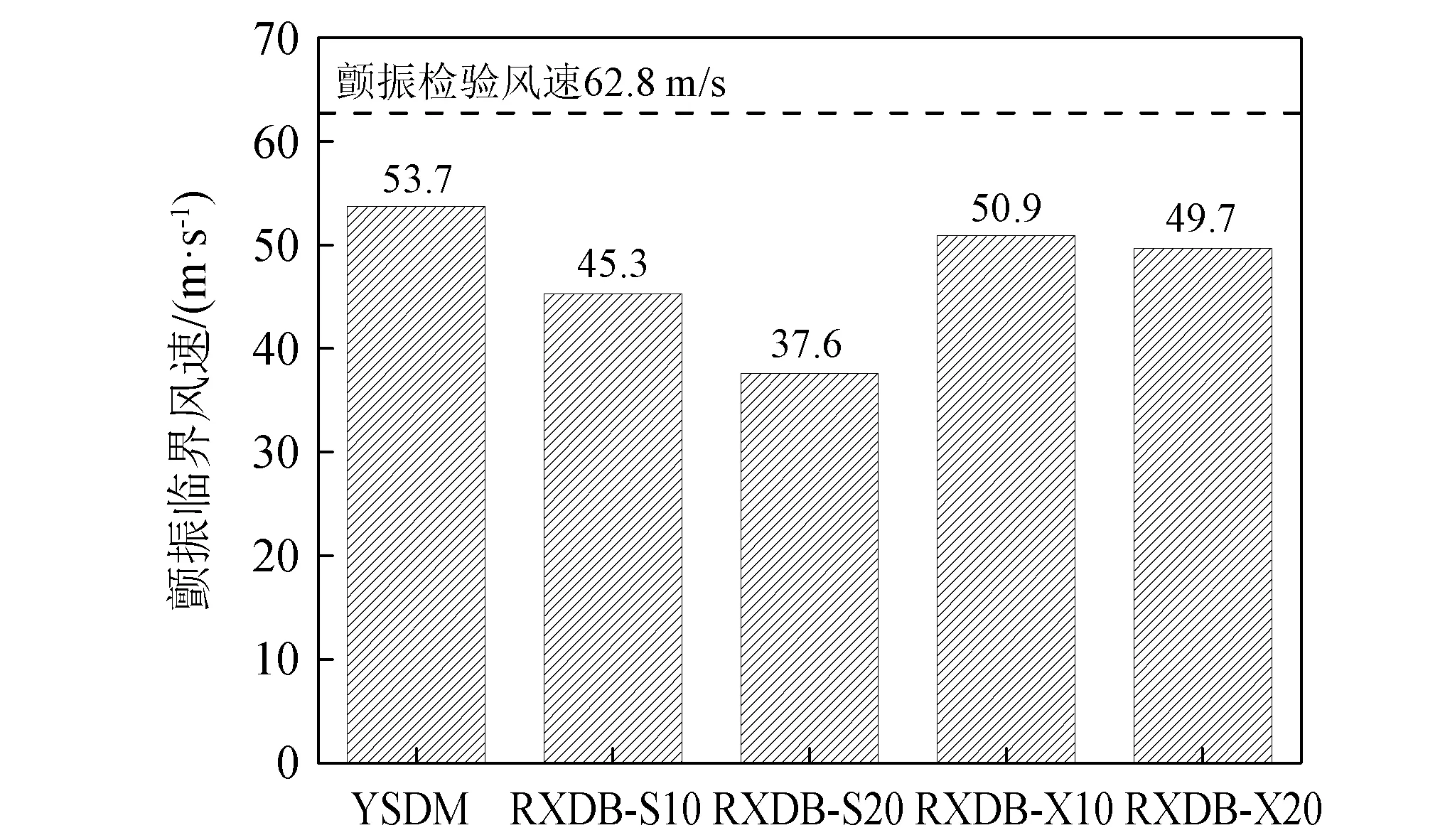
图9 RXDM工况-3°攻角颤振临界风速Fig.9 Flutter critical wind speed of RXDM section with attack angle of -3°

3.4 水平稳定板

根据RXDB工况的试验结果可知，当人行道板处于0°倾角时断面颤振稳定性较好，故在0°倾角人行道板(YSDM)基础上分别设置长度为1.1 m与2.1 m的水平稳定板，措施具体细节如图10所示，并通过1∶50节段模型风洞试验测试了0°与±3°风攻角下水平稳定板对该桥主梁颤振临界风速的影响。

图10 SPDM工况断面示意图Fig.10 Diagram of SPDM section

各工况下主梁颤振临界风速如图11所示，可以发现水平稳定板会显著降低断面在0°与-3°攻角下的颤振临界风速，且降幅随着水平稳定板长度的增加而增大，但在+3°攻角下，断面颤振临界风速随着水平稳定板长度的增加先增大后减小，当水平稳定板长度为0.021B(1.1 m)时提升作用最为显著，颤振临界风速较不设置水平稳定板时提高16.1%，增大稳定板长度至0.041B(2.1 m)后提升作用降低至13.5%。

通过图11中的颤振临界风速下包络线对断面的综合颤振稳定性进行评估，可以发现由于水平稳定板会显著降低-3°攻角下断面的颤振临界风速，设置水平稳定板后，对断面颤振稳定性起控制作用的主要是-3°攻角，当水平稳定板高度在0.021B时优化效果达到最佳。

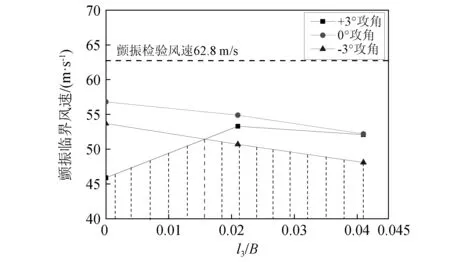
图11 SPDM工况颤振临界风速Fig.11 Flutter critical wind speed of SPDM section

3.5 斜导流板

取前文各试验工况中颤振稳定性最佳的工况SXWDM-0.8，在此工况断面基础上，在人行道板端部设置倾角为45°的斜导流板，措施具体细节如图12所示，斜导流板长度分别为0.9 m与1.2 m，并通过1∶50节段模型风洞试验测试了XDDM工况断面在0°与±3°风攻角下的颤振临界风速。

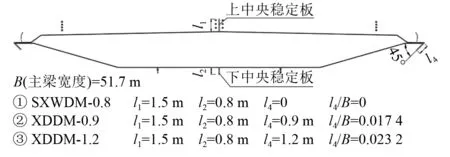
图12 XDDM工况断面示意图Fig.12 Diagram of XDDM section

各工况下主梁颤振临界风速如图13所示，可以发现1.2 m(0.023 2B)长的斜导流板可以显著提高各攻角下断面的颤振稳定性，能够在上、下中央稳定板的优化作用下进一步提升各攻角下断面的颤振临界风速5%以上，且优化后断面在0°与±3°攻角下的颤振临界风速均能高于颤振检验风速(62.8 m/s)，满足主梁颤振设计要求。

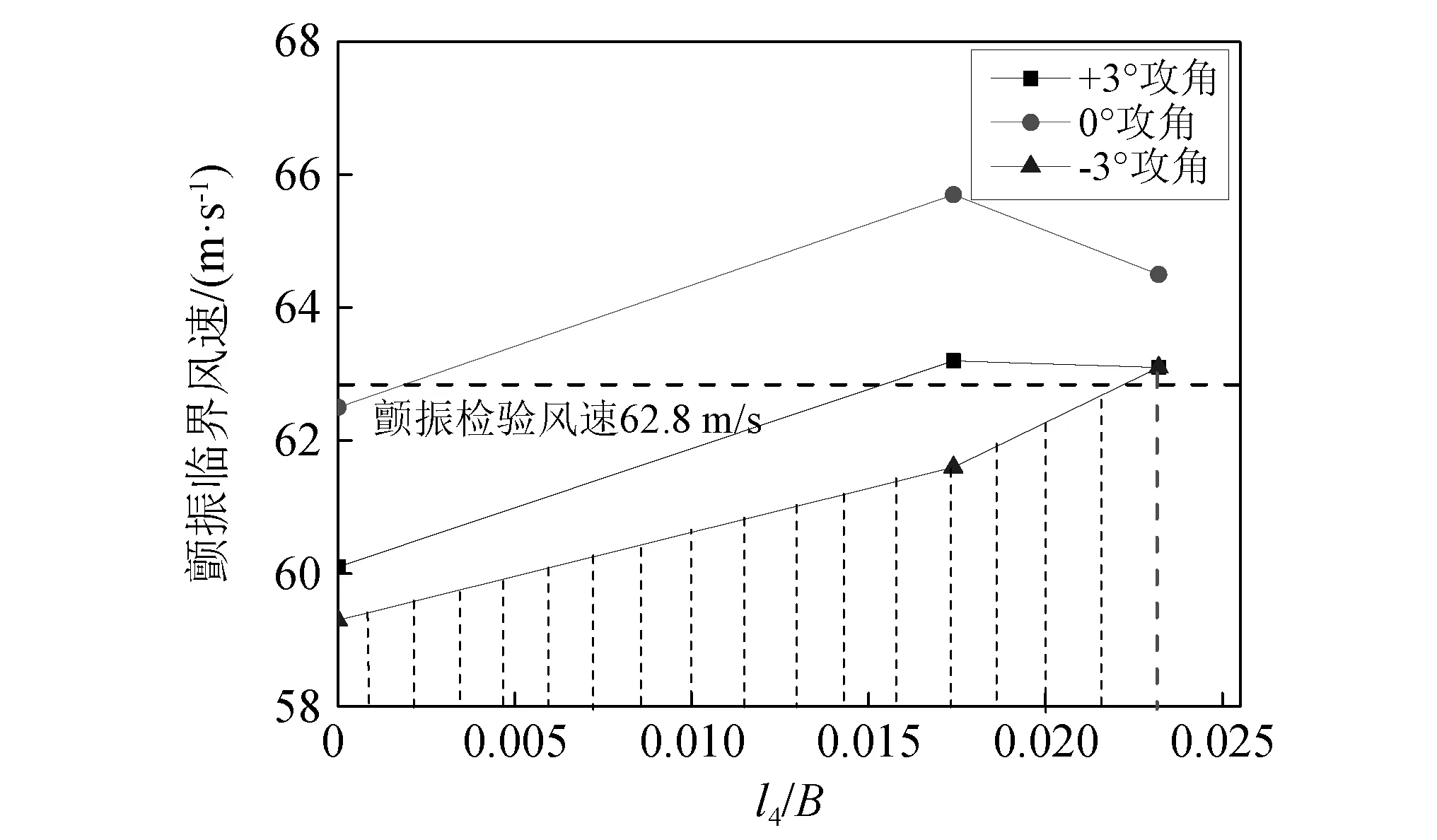
图13 XDDM工况颤振临界风速Fig.13 Flutter critical wind speed of XDDM section

降低导流板长度至0.9 m(0.017 4B)后，虽然0°与+3°攻角下断面颤振临界风速得到进一步提升，但-3°攻角下断面颤振临界风速发生显著降低且不满足颤振设计要求，断面的综合颤振稳定性反而降低。

综上可以发现，在原设计断面基础上同时设置1.5 m上中央稳定板、0.8 m下中央稳定板与1.2 m斜导流板所形成的XDDM-1.2工况断面在0°与±3°攻角下均能满足颤振设计要求，且较原设计断面各攻角下的颤振临界风速提高率均在13.6%以上。

4 全桥气弹模型风洞试验

与节段模型相比，全桥气弹模型的动力特性、气动外形以及试验流场可以较真实的模拟实际情况，同时能够较好地反映三维空间效应和多模态耦合效应，从而获得更接近实桥颤振响应的试验结果[17-20]。因此有必要对采用XDDM-1.2断面为主梁截面的张皋过江通道南航道桥进行全桥气弹模型风洞试验，用以验证气动措施的有效性。

全桥气弹模型风洞试验在西南交通大学大型低速风洞(XNJD-3)中进行，该风洞为回流式风洞，试验段截面尺寸为22.5 m(宽)×4.5 m(高)×36.0 m(长)。考虑到桥长以及风洞试验段的尺寸，全桥气弹模型采用1∶196的几何缩尺比，风速比为1∶14。

全桥气弹模型由主梁、桥塔、大缆、吊索以及支座等构成(如图14所示)，由于缩尺后模型质量要求较低，为严格满足弗洛德数的一致性条件，采用轻质巴尔杉木模拟主梁的几何外形(主跨节段外模细节如图15所示)，在加劲梁的扭转中心用“凹”字形钢芯梁模拟加劲梁的竖向、横向和扭转刚度刚度，并由铝制芯梁提供桥塔的弯曲刚度，具体试验参数如表6所示。

图14 全桥气弹模型Fig.14 The full bridge aeroelastic model

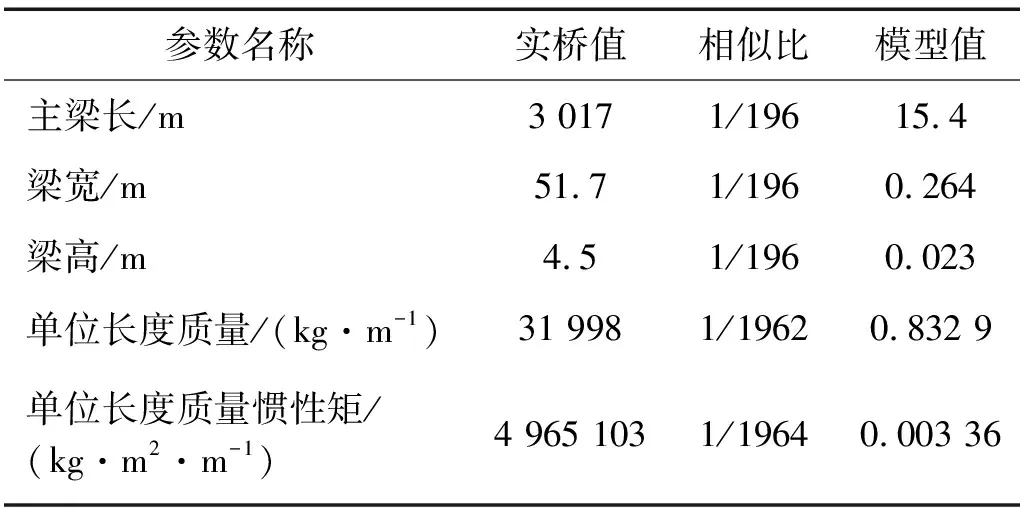
表6 全桥气弹模型试验参数

为了检验模型的结构动力特性是否与原型计算值之间满足相似关系，采用激光位移传感器及振动分析系统CRAS对全桥气弹模型进行模态测试。由于悬索桥在发生颤振时，主要是低阶频率起控制作用，因此在测试模型动力特性过程中，主要对竖向、扭转和侧向三个方向上的基频进行了检验，测试结果如表7所示，结果表明模型频率实测值与要求值相比，误差均在2%以内，因此可以认为该气弹模型的动力特性满足要求，可代表原结构的风致动力行为。

图15 主跨节段外模细节图Fig.15 Detail of main span section

表7 全桥气弹模型模态参数

全桥气弹模型风洞试验在均匀流中进行，各风攻角下的颤振临界风速测试结果如表8所示(表中数据均已换算至实桥)，可以发现0°与±3°风攻角下，全桥气弹模型风洞试验与节段模型风洞试验所获得的颤振临界风速存在一定差异，但两者均高于颤振检验风速，其中通过全桥气弹模型试验所得到的值较高。

表8 XDDM-1.2断面颤振临界风速

综上所述，节段模型风洞试验与全桥气弹模型风洞试验均验证了上、下中央稳定板与斜导流板组合形成的气动措施对该扁平钢箱梁断面颤振稳定性的提高作用，采用加装该组合气动措施的断面(XDDM-1.2)作为主梁断面后该桥能够在0°与±3°攻角下均达到颤振设计要求。

5 结 论

张皋过江通道南航道桥跨度大、桥面宽，整体结构柔度较大，对风的作用极其敏感。本文通过节段模型风洞试验和全桥气弹模型风洞试验优化和比选了气动措施。得出主要结论如下：

(1)针对本文所示的扁平钢箱梁，单独设置上中央稳定板可以有效提高主梁颤振临界风速，在上中央稳定板基础上加装一定高度(0.27H)范围内的下中央可以进一步优化断面的颤振稳定性，但超过该高度后，下中央稳定板会对上中央稳定板的优化效果起到降低的作用。

(2)人行道板上翘或下倾均会显著降低该扁平箱梁在-3°风攻角下的颤振临界风速，当人行道板处于水平状态(0°)时主梁颤振稳定性较好。

(3)在人行道板端部设置水平稳定板可有效提高主梁在+3°风攻角下的颤振临界风速，但同时会显著降低0°与-3°风攻角下主梁的颤振临界风速。

(4)在设置1.5 m上中央稳定板与0.8 m下中央稳定板的基础上，通过在人行道端部设置斜导流板可显著提高该扁平箱梁在各攻角下的颤振临界风速，当斜导流板长度为1.2 m时提升效果最佳(XDDM-1.2工况)，通过全桥气弹模型对该措施的颤振优化性能进行了检验，试验结果表明，加装该组合气动措施后，该桥在0°与±3°攻角下均能达到颤振检验风速，满足颤振设计要求。

作为主跨2 300 m超大跨度悬索桥，张皋过江通道南航道桥开创性地采用了整体钢箱梁，与同为2 000 m级的土耳其恰纳卡莱大桥所采用的分体钢箱梁相比，在颤振稳定性方面提出更高的挑战与要求，同时也促进了整体钢箱梁用于大跨度悬索桥跨径极限的研究。本文开创性的提出了在人行道板处设置斜导流板用于提高扁平箱梁的颤振稳定性，但引起该变化的流场机理与颤振控制机理尚未明确，在后续研究中将通过CFD数值模拟以及测试颤振导数的变化等方法对该问题进行深入研究。