400 km/h高速铁路桥梁竖向刚度限值研究
2022-08-05向活跃陈绪黎李永乐
向活跃, 陈绪黎, 张 玲, 李永乐
(1. 西南交通大学 土木工程学院,成都 610031; 2. 中铁第四勘察设计院集团有限公司,武汉 430063)
随着我国铁路行业的高速发展,高速铁路里程显著增加,截至2020年底达3.79万km。响应“客运高速、货运重载”的运输发展方向,建设运营设计400 km/h及以上的高速铁路已提上日程[1-2]。车速增加必然会对桥梁设计提出更高要求,竖向刚度限值作为控制桥梁变形的重要指标,对列车运营安全性和乘坐舒适性有显著影响,现行TB 10002—2017《铁路桥涵设计规范》[3](后文简称铁路桥规)适用于350 km/h及以下车速,研究400 km/h高速铁路桥梁的刚度限值有重要研究意义。
高速列车通过桥梁会激起桥梁振动,桥梁振动又会反作用于车辆,车速增加时,车桥动力响应也会进一步增加,过低的桥梁刚度可能会导致桥面坡度超限、乘坐不适、甚至列车脱轨等现象发生[4],所以各国规范对竖向刚度限值做出严格要求,具有代表性的有日本[5]、UIC[6]和中国等相关规范。刚度限值通常可采用桥梁竖向挠度限值表示,当主梁竖向挠度较大时支座转角通常也较大,线路不再平顺连续,所以铁路桥规对梁端竖向转角也进行了限值规定[7],本文将同时考虑桥梁竖向挠度限值和梁端竖向转角限值的影响。
沈锐利[8]在不考虑桥梁振动情况下,使用整车模型计算车辆通过不同跨度的单跨简支梁和多跨连续布置的等跨度简支梁桥的最大挠跨比,对高速铁路桥梁的刚度限值有一定参考意义。高岩等[9]采用23自由度车辆模型,通过改变桥梁截面刚度,基于车桥耦合振动分析方法,计算7种中小跨度单跨和等跨度多跨简支梁桥的竖向刚度限值。翟婉明等[10]采用国产高速列车和32 m简支梁桥进行动力相互作用分析,通过调整桥梁截面惯性矩改变桥梁竖向刚度,研究桥梁刚度较小时列车—轨道—桥梁耦合系统的动力特性变化。李奇等[11]考虑桥梁徐变、温度、桥墩沉降等影响下的静态变位,采用CRH3高速列车和不同跨度的简支梁桥进行车桥耦合振动分析,改变桥梁刚度得到车辆安全性、舒适性指标,计算车辆响应指标达到限值时在设计活载作用下的挠跨比,即为桥梁竖向刚度限值。
从已有研究和现行设计规范发现,不同车速条件下,不同跨度桥梁的竖向刚度要求差异大,且多针对车速350 km/h及以下高速铁路,对400 km/h高速铁路桥梁竖向刚度研究较少。
本文基于铁路桥规数据分析400 km/h高速铁路桥梁的刚度限值;然后,按规范中跨度划分范围选取3种跨度桥梁,采用时速400 km/h高速列车参数,基于车桥耦合振动分析方法,并考虑车速、车辆载重、车辆编组和桥型等因素的影响,对桥梁竖向挠度限值和梁端竖向转角限值进行分析;最后得到400 km/h高速铁路桥梁竖向刚度限值的参考值。
1 基于现行规范数据的分析
根据铁路桥规和文献[12]研究,竖向刚度限值指标可按竖向挠度和梁端竖向转角两部分考虑。铁路桥规中按不同车速及跨度条件给出竖向挠度限值,设计时在ZK荷载作用下梁体竖向挠度限值规定,如表1所示。表1中L为桥梁跨度,三跨及以上一联的连续梁挠度限值需按表中数值1.1倍取用。根据表1中3种跨度范围桥梁在车速250 km/h,300 km/h,350 km/h的竖向挠度,按二次项拟合得到车速400 km/h的竖向挠度,拟合曲线如图1所示。
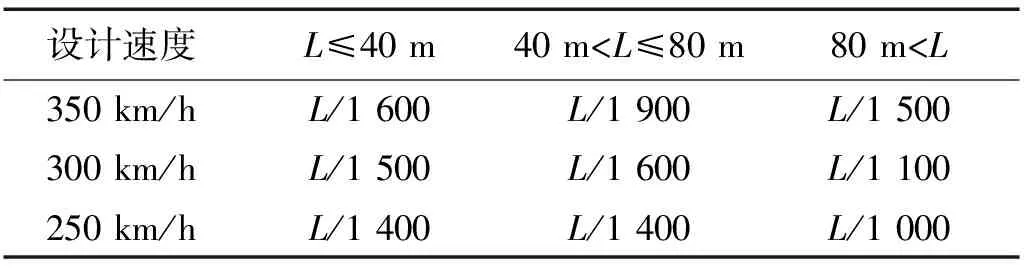
表1 梁体竖向挠度限值Tab.1 The limit of vertical deflection of beam
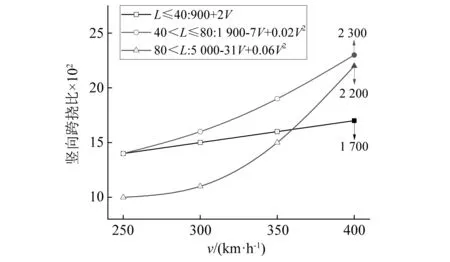
图1 竖向挠度拟合曲线Fig.1 Fitting curve of vertical span deflection ratio
由图1可见,当车速为400 km/h时,L≤40 m竖向挠度限值为L/1 700,40 m 按铁路桥规要求,根据梁端悬出长度对梁端竖向转角进行取值,无需考虑车速、桥型和跨度条件等因素的影响。 我国尚未建成400 km/h高速铁路线路,无法通过试验获得线路中桥梁的刚度指标,为进一步确定400 km/h 高速铁路桥梁的竖向刚度限值,可采用车-桥耦合振动分析方法进行研究。 时速400 km/h高速列车与时速350 km/h高速列车的动力学参数有一定差异,但车辆结构基本相似,仍可看作两系悬挂质量弹簧阻尼车[13],如图2所示。每节车辆由1个车体、2个转向架和4个轮对共7部分刚体以及弹簧、阻尼元件组成,车体和转向架考虑5个自由度,轮对仅考虑横移和摇头2个自由度,整车为23自由度。根据达朗贝尔原理,可得车辆的运动方程 (1) 时速400 km/h高速列车,头车长28.064 m,中间车长25.650 m。研究中,车辆编组考虑8车和16车两种编组,车辆载重考虑空载和满载两种情况,共有8编组空载、8车编组满载、16车编组空载和16编组满载4种车辆工况;车速考虑350 km/h和400 km/h。 图2 23自由度车辆模型Fig.2 23 degree of freedom train model 分析中,桥梁均为无砟轨道预应力混凝土双线桥,桥梁跨中截面形式如图3所示。在有限元软件中使用Beam4梁单元进行建模,经动力特性分析,得到桥梁自振频率、总体质量矩阵和总体刚度矩阵等信息,桥梁阻尼比为0.02,由Rayleigh阻尼计算公式可计算桥梁总体阻尼矩阵。桥梁子系统的运动方程[14]可写作 (2) 图3 桥梁跨中截面示意图Fig.3 Schematic diagram of bridge mid-span section 分析中,采用15跨32 m简支梁桥、32 m+48 m+32 m连续梁桥和72 m+128 m+72 m刚构桥进行400 km/h高速铁路桥梁竖向刚度限值研究。简支梁桥和连续梁桥主梁采用C50混凝土,刚构桥主梁采用C55混凝土。简支梁桥和连续梁桥桥墩采用C40混凝土,刚构桥边墩和中墩分别采用C35和C40混凝土,桥墩均为空心墩,墩高均为50 m,文献[15]研究表明墩高对梁体竖向动力响应影响较小。3种桥梁的竖向基频和跨中截面惯性矩信息,如表2所示。 表2 桥梁模型结构信息Tab.2 Structural information of bridge model 根据几何相容条件和静力平衡条件[16],车辆子系统运动方程和桥梁子系统运动方程进行分离迭代,轮轨接触采用德国低干扰谱,空间步长取为0.2 m,并使用AR法[17]生成轨道不平顺样本。借助自主研发软件Bansys进行车桥耦合振动分析。 计算时分为两步:第一步基于车桥耦合振动分析方法,计算不同桥梁竖向刚度时的车辆响应; 第二步将各刚度的桥梁模型按规范条件进行加载计算竖向挠度和梁端竖向转角,车辆响应超限时对应的桥梁竖向刚度即为竖向刚度限值。 为方便设计,提出的刚度限值仍需采用已有规范的加载形式。双线桥梁需在结构最不利位置加载100%的ZK荷载,加载时列车荷载图式可按影响线长度任意截取,在同符号影响线区段加载ZK荷载,异符号影响线区段大于15 m时加载10 kN/m,小于15 m时不进行加载。32 m简支梁桥计算竖向刚度和梁端转角的荷载加载图示相同,如图4(a)所示;根据32 m+48 m+32 m连续梁桥和72 m+128 m+72 m刚构桥的中跨跨中弯矩影响线,竖向刚度计算加载图示如图4(b)和图4(c)所示,根据边跨跨中弯矩影响线,梁端转角计算加载图示如图5所示。 图4 竖向挠度限值加载示意图Fig.4 Loading diagram of vertical deflection limit 图5 梁端转角限值加载示意图Fig.5 Loading diagram of girder-end rotation limit 按铁路桥规要求,对于连续梁桥等超静定结构,计算竖向刚度时需考虑温度变形的影响。温度变形包含均匀温差和日照温差两部分变形,形式和大小可参考TB 10092—2017《铁路桥涵混凝土结构设计规范》[18]。均匀温差从合龙时的温度算起,考虑整体升降温 20 ℃。日照温差为指数形式,如图6所示,沿箱梁高度方向上的温度大小计算如式(3)所示 Ty=T01e-ay (3) 式中:Ty为计算点y处的温差;T01为箱梁梁高方向温差,考虑铺设无砟轨道后,梯度升温时取为10 ℃,梯度降温时取为-5 ℃;a在升温时取为5 m-1,降温时取为14 m-1。 图6 箱梁竖向温差分布图Fig.6 Vertical temperature difference distribution of box girder 由于进行车桥耦合振动计算时,通过降低截面惯性矩的方式实现不同桥梁刚度,梁刚度不同时截面尺寸应有所区别,为简化计算,温度效应计算中仍采用原尺寸,使用MIDAS Civil软件计算各刚度桥梁的温度变形。 计算桥梁竖向刚度时,通过降低桥梁模型竖向惯性矩,并保证其他参数均不变的条件下,基于车桥耦合振动分析计算车辆动力响应;同时,按铁路桥规要求对降低竖向惯性矩的相应桥梁模型在最不利位置进行加载得到桥梁变形,从而建立车辆动力响应与桥梁竖向刚度之间的关系。车辆响应在限值处的桥梁竖向刚度,即为桥梁结构设计时竖向刚度限值,具体步骤如下。 步骤1竖向挠度限值 ①按1/5、1/8、1/10、1/12、1/14、1/16、1/18乘以桥梁竖向惯性矩,降低桥梁竖向刚度,计算不同刚度倍数下桥梁的竖向温度变形; ②将各刚度倍数下的桥梁竖向温度变形按0.2 m的间隔进行插值,叠加至轨道高低不平顺,进行车桥耦合振动分析,获得车辆响应。以刚度下降1/18倍为例,3种桥梁进行车桥耦合计算时的轨道高度不平顺如图7所示,32 m简支梁桥挠度限值不考虑温度作用,轨道高低不平顺中不叠加竖向温度变形。 图7 轨道高低不平顺Fig.7 Track vertical irregularity ③各刚度倍数下,32 m简支梁桥、32 m+48 m+32 m连续梁桥、72 m+128 m+72 m刚构桥分别按图4(a)、图4(b)、图4(c)加载ZK荷载,得到桥梁在ZK荷载作用下的最大竖向挠度,将各桥梁ZK荷载和0.5倍温度引起的竖向挠度之和与0.63倍ZK荷载和全部温度引起的竖向挠度之和进行比较,并取两者中的大值最为桥梁竖向挠度。 ④将各刚度倍数下的车辆响应和桥梁竖向挠度一一对应,插值计算车辆响应限值时的桥梁竖向挠度限值,并与铁路桥规的竖向挠度限值进行比较,判断现行铁路桥规的竖向挠度限值对400 km/h高速铁路桥梁的适应性。 步骤2梁端竖向转角限值 ①按1/5、1/8、1/10、1/12、1/14、1/16、1/18乘以桥梁竖向惯性矩,从而降低桥梁竖向刚度,轨道高低不平顺中不考虑温度变形,进行车桥耦合振动分析,获得车辆响应。 ②各刚度倍数下,32 m简支梁桥按图4(a)、32 m+48 m+32 m连续梁桥按图5(a)、72 m+128 m+72 m刚构桥图5(b)加载ZK荷载,得到桥梁最大梁端转角。 ③将各刚度倍数下的车辆响应和桥梁最大梁端转角进行对应,插值计算车辆响应限值时的梁端竖向转角限值,并与现行规范的梁端竖向转角限值进行比较,判断现行铁路桥规的转角限值是否适用于400 km/h高速铁路桥梁。 为保证列车运营安全性和乘坐舒适性,铁路桥规对车辆的安全性和舒适性作出了相应的规定,其中车辆限值指标适用于车速350 km/h及以下工况。加速度指标反映人体舒适性,其限值要求不应随车速的增加而改变,车辆安全性指标在车速400 km/h如何取值有待进一步研究。本文的车桥耦合振动分析表明,车辆竖向加速度最早达到规范限值(1.3 m/s2),欧洲规范和日本规范也表明控制桥梁刚度是主要是为满足乘坐舒适度。考虑到车辆舒适性指标通常较安全性指标更加严格,因此以车辆的加速度响应指标进行后续分析。 通过车桥耦合振动分析,计算得到3种桥梁的竖向挠度限值如图8所示。由图8可见,当车速为400 km/h时,32 m简支梁桥的竖向挠度限值为L/882,大于规范限值L/1 700;32 m+48 m+32 m连续梁桥竖向挠度限值为L/750,大于规范限值L/2 090; 72 m+128 m+72 m刚构桥的竖向挠度限值为L/1 584,大于规范限值L/2 000;当车速为350 km/h时,计算得到的竖向挠度限值也均大于规范限值。车速400 km/h较车速350 km/h计算得到的竖向挠度限值变小,约减少8%~18%,车速更高时竖向挠度限值要求更加严格。当桥梁竖向刚度下降到一定程度时,车辆竖向加速度变化加快。 图8 3种桥梁竖向挠度限值Fig.8 The limit of vertical deflection of three kinds of bridges 车桥耦合振动分析中,车辆响应受随机轨道几何不平顺的影响,会导致车辆响应会有一定的差异。同时,轨道几何不平顺在不同位置与温度变形叠加时也会导致车辆响应的计算结果有一定的差异。部分研究是通过乘以安全系数的方式来考虑随机性的影响[19]。从高速列车响应随机性的研究结果看,受轨道几何不平顺随机性的影响,车辆竖向加速度在超越概率为10-4时的数值与最小值相差约一倍,其计算中采用的是32 m简支梁桥[20]。对比图8(a)计算结果可见,当车速为350 km/h和400 km/h时,计算的挠度限值在考虑2.0的安全系数后,与现行规范值和外推值均较为吻合。在其他两种桥梁跨度中,两种车速下计算的竖向挠度限值均大于现行规范值及其外推值,表明规范对竖向挠度限值要求更加严格,且具有合理的安全储备。 考虑规范规定的连续性,所以400 km/h高速铁路桥梁竖向挠度限值可采用现行规范由车速250 km/h,300 km/h,350 km/h拟合外推得到的400 km/h的竖向挠度限值,即,L≤40 m竖向挠度限值取为L/1 700,40 m 规范对不同梁端悬出长度的高速铁路桥梁做出梁端转角限值规定,32 m简支梁桥、32 m+48 m+32 m连续梁桥和72 m+128 m+72 m刚构桥的梁端悬出长度分别为0.55 m,0.75 m和0.70 m,简支梁桥共有15跨,可考虑桥梁与桥台梁端竖向转角限值θ、相邻两孔梁每孔梁梁端竖向转角限值θ以及相邻两孔梁梁端竖向转角限值之和θ1+θ2,连续梁桥和刚构桥只考虑桥梁和桥台处的梁端竖向转角限值θ,3种桥梁梁端竖向转角限值如表3所示。 表3 梁端竖向转角规范限值Tab.3 The limit of vertical girder-end rotation in code 通过车桥耦合振动分析,计算得到3种桥梁的梁端竖向转角限值如图9所示。图9显示,当车速为400 km/h时,32 m简支梁桥桥梁与桥台梁端竖向转角为2.71‰ rad,相邻两孔梁每孔梁梁端竖向转角为3.47‰ rad,均大于规范限值1.5‰ rad,相邻两孔梁梁端竖向转角之和为6.17‰ rad,大于规范限值3‰ rad;32 m+48 m+32 m连续梁桥、72 m+128 m+72 m刚构桥桥梁与桥台梁端转角为2.05‰ rad,1.37‰ rad,均大于规范限值1‰ rad。车速400 km/h较350 km/h的计算得到的梁端转角限值变小,减少约16%~20%,梁端竖向转角限值要求更加严格。铁路桥规也指出无砟轨道大跨度桥梁的梁端转角限值往往成为梁体刚度设计控制指标,本文中3种跨度桥梁随跨度增加而梁端竖向转角限值减小,这与铁路桥规的结论一致。 图9 3种桥梁梁端竖向转角限值Fig.9 The limit of girder-end rotation of three kinds of bridges 通过比较铁路桥规和车辆加速度限值对应的梁端竖向转角限值,车速400 km/h计算得到的梁端竖向转角限值较车速350 km/h减少约16%~20%,但仍大于铁路桥规限值,有一定安全储备,所以车速为400 km/h的高速铁路桥梁梁端竖向转角限值仍可采用铁路桥规限值,即梁端悬出长度不超过0.55 m时,桥台与桥梁之间梁端竖向转角限值为1.5‰ rad,相邻两孔梁梁端竖向转角之和限值为3‰ rad;梁端悬出长度不超过0.75 m时,桥台与桥梁之间梁端竖向转角限值为1‰ rad,相邻两孔梁梁端竖向转角之和限值为2‰ rad。 利用铁路桥规数据外推和车桥耦合振动的方法研究400 km/h高速铁路桥梁的竖向挠度限值与梁端竖向转角限值,分析相应的竖向刚度建议值,得出以下结论: (1) 车桥耦合振动计算值较规范数据外推值大,竖向挠度限值的要求随车速的增加而提高,考虑随机性及规范规定连续性的影响,建议400 km/h高速铁路桥梁跨度L≤40 m,竖向挠度限值为L/1 700,40 m (2) 基于车桥耦合振动分析,车速400 km/h时的梁端竖向转角较350 km/h减少约16%~20%,但仍然大于铁路桥规梁端竖向转角限值,有一定安全储备,建议400 km/h高速铁路桥梁梁端竖向转角限值仍可根据梁端悬出长度按现行规范限值取值。2 车桥耦合模型
2.1 车辆模型


2.2 桥梁模型
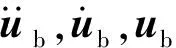

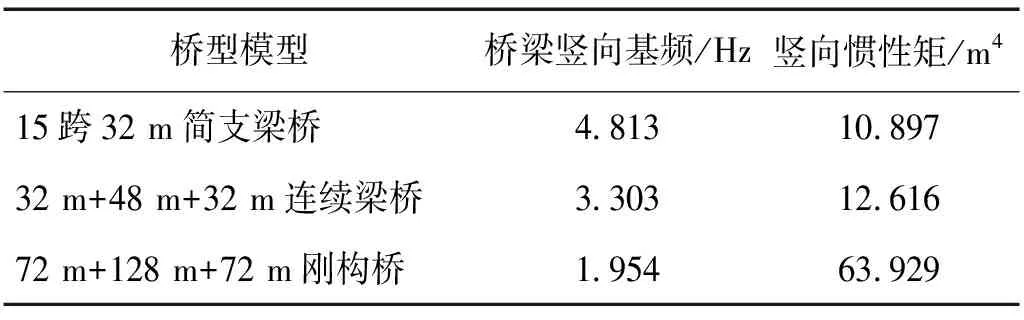
3 竖向刚度限值的计算方法
3.1 按规范条件加载
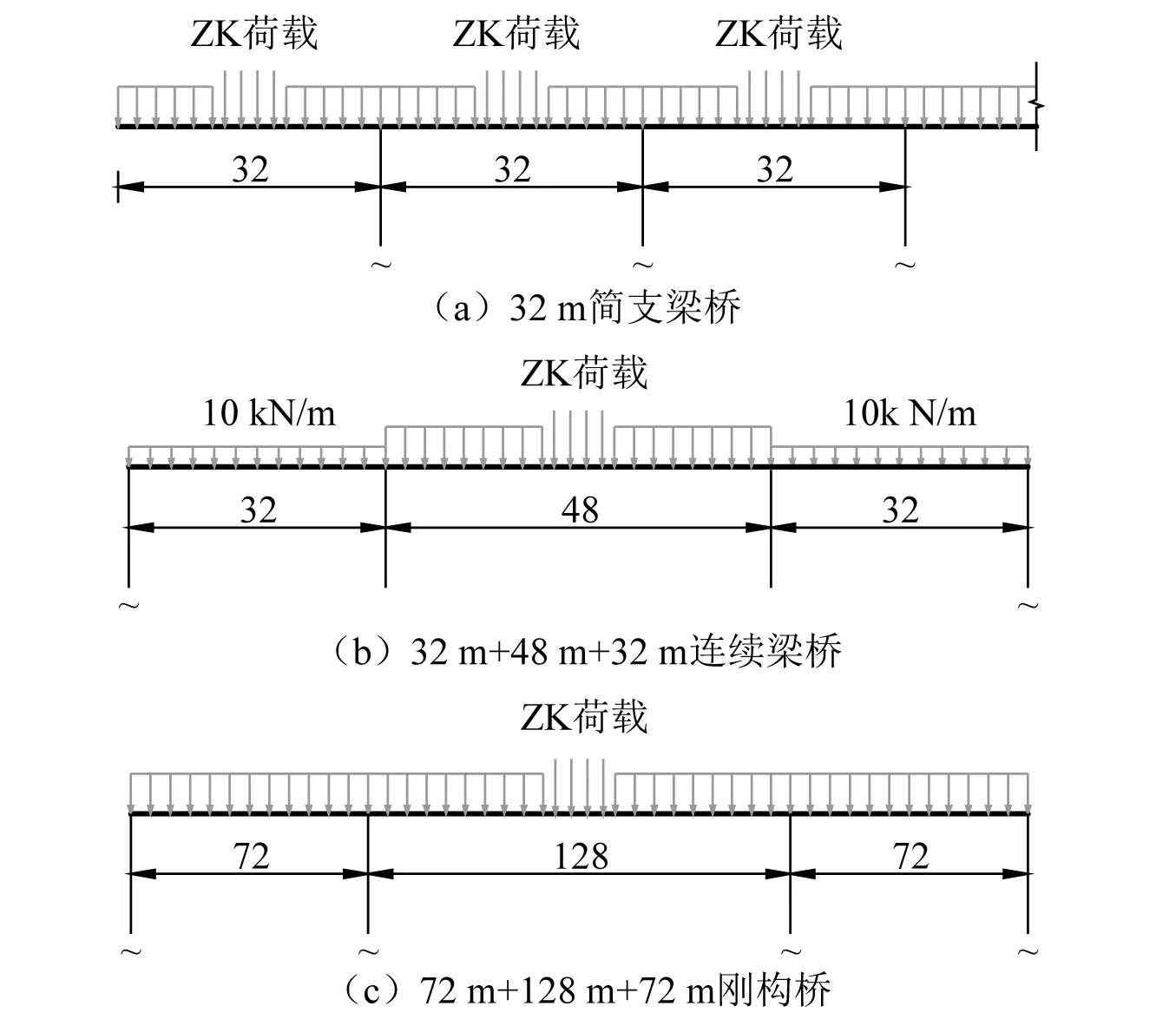
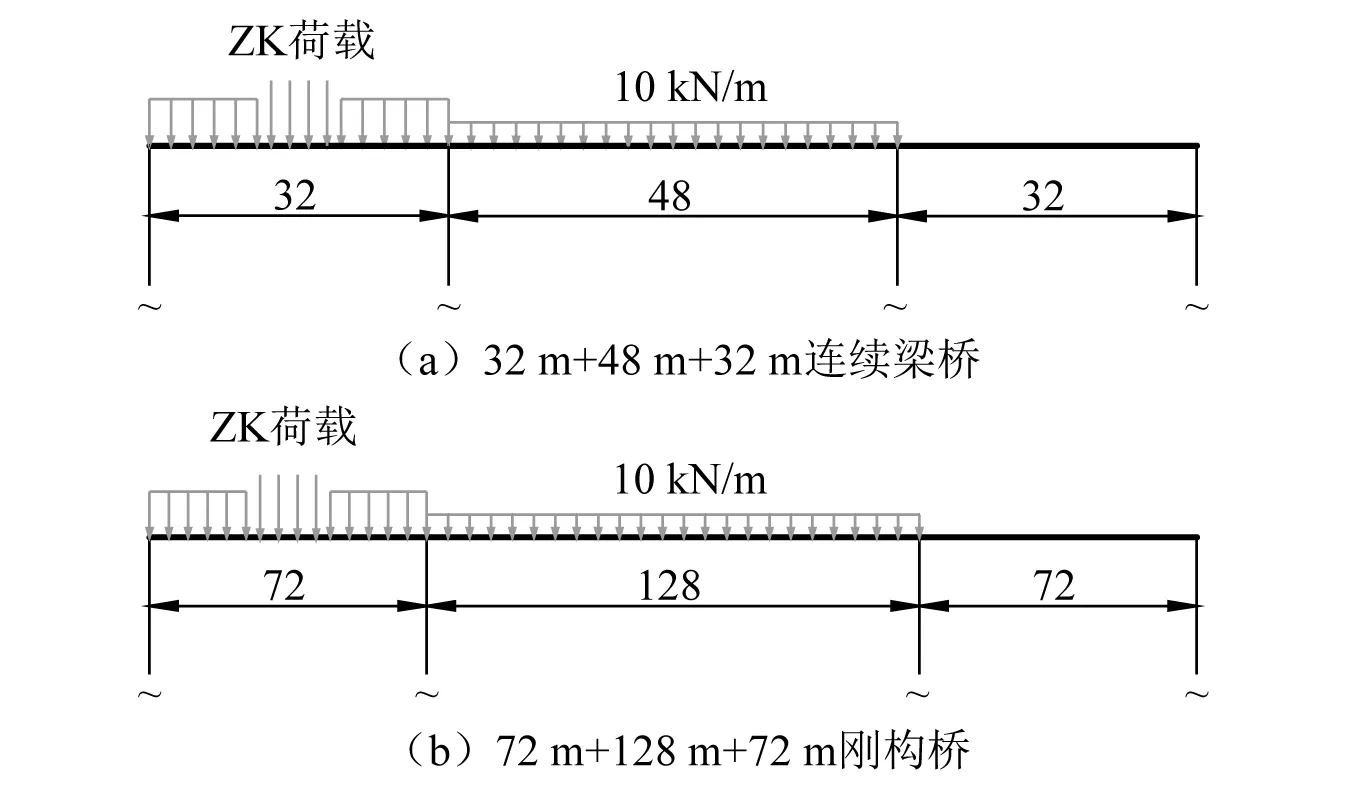
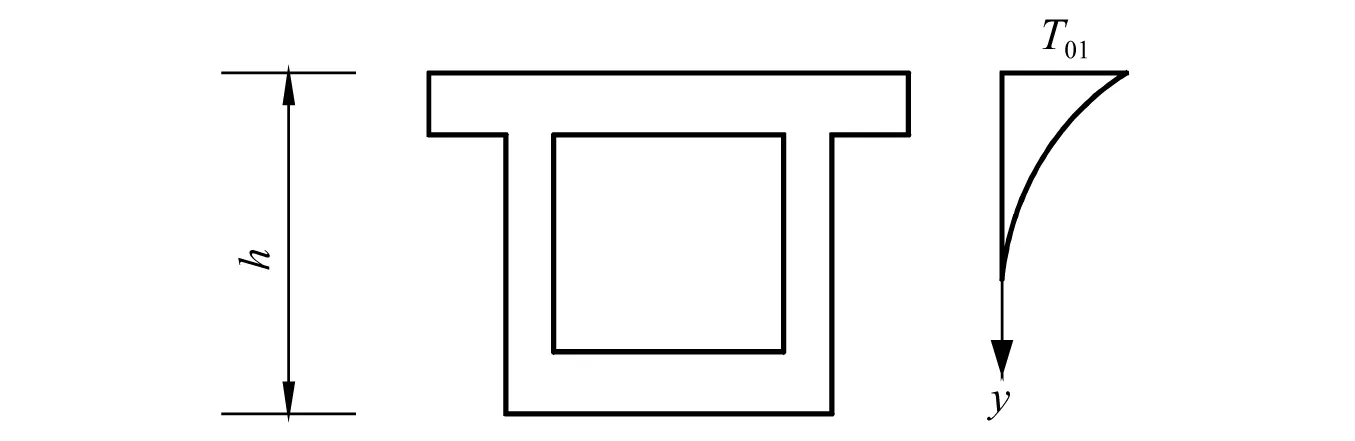
3.2 计算步骤
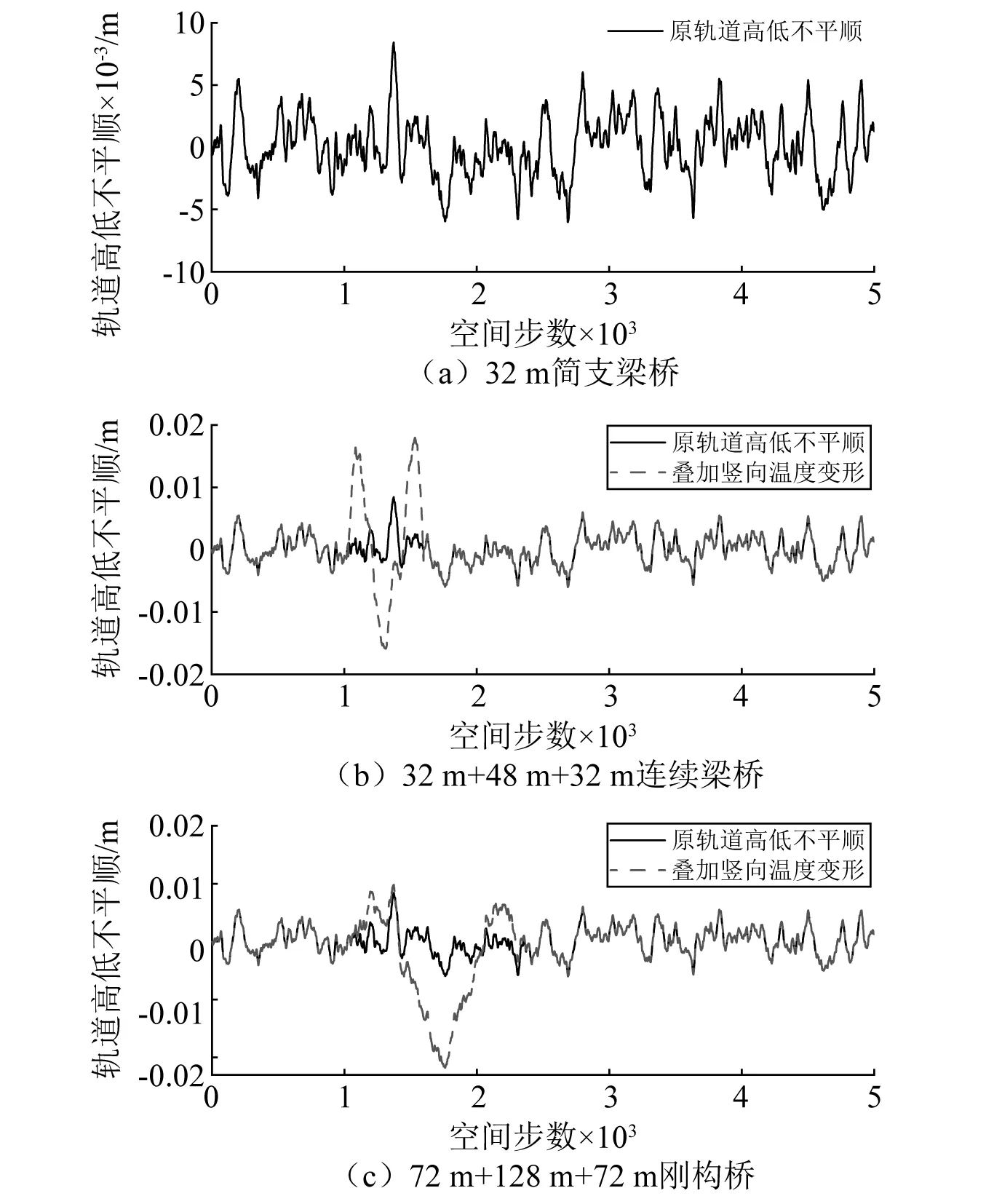
4 结果分析
4.1 竖向挠度限值

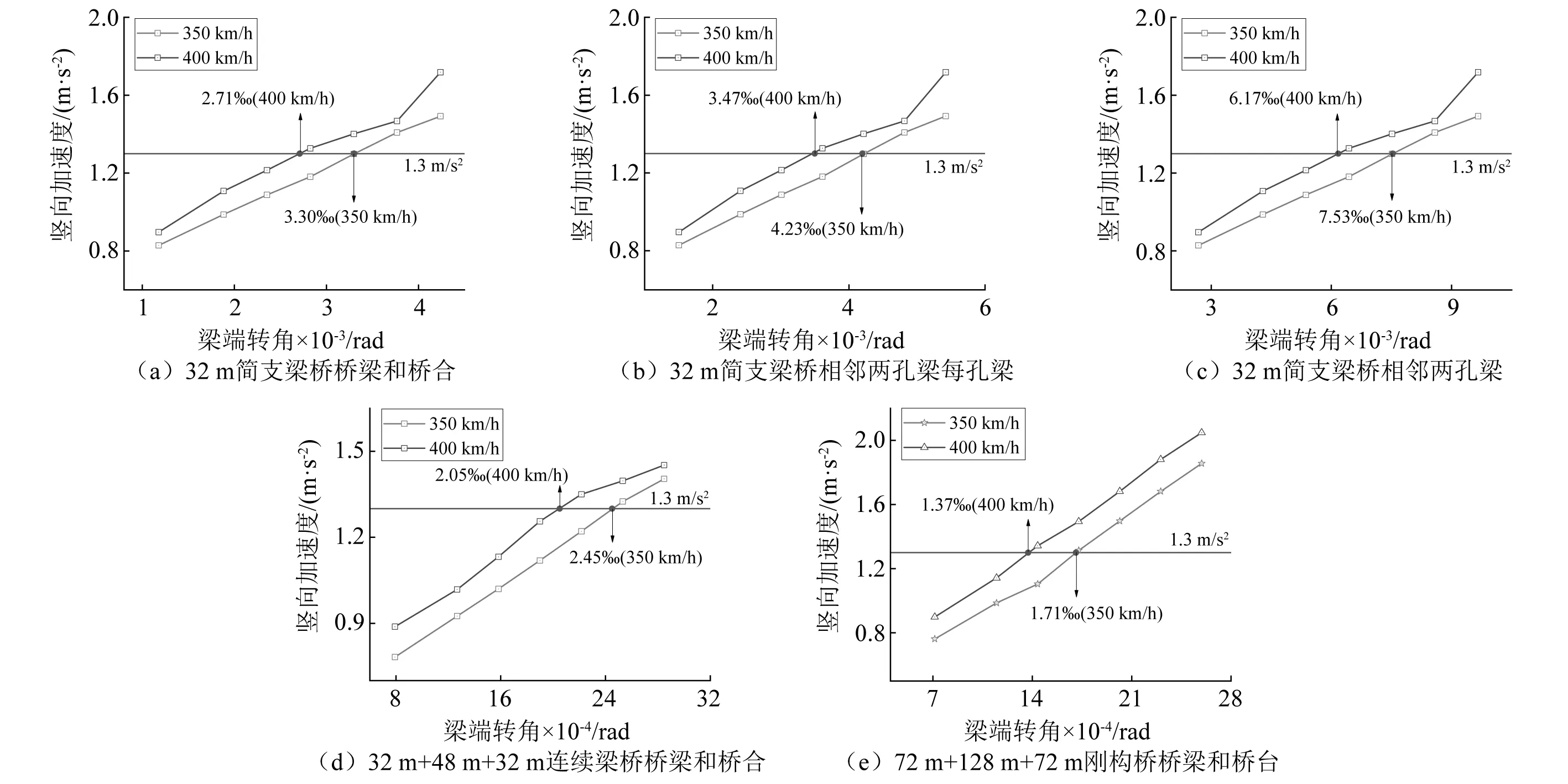
4.2 梁端转角限值

5 结 论
