杠杆式隔振器的理论模型及隔振特性研究

王志豪， 潘侠圭， 武传宇， 严 博

(浙江理工大学 机械与自动控制学院，杭州 310018)

机械振动响应已是高、精、尖装备研发和先进制造领域前沿技术中的共性问题，也是亟需解决的关键技术问题。因此，为了降低振动响应，隔振[1-5]、吸振[6]、阻尼减振及振动主动控制[7-8]等方式得到广泛应用。此外，也可以通过力电转化机制，将有害振动转化为电能，供低功耗电子器件使用[9]。

隔振是一种应用较为广泛的可在较宽频率范围内抑制振动的方式。线性隔振器原理简单，易于加工，因此，得到了极为广泛的应用。随着结构轻量化、轻质复合材料的应用，系统的固有频率呈现下降趋势。传统线性隔振器需要降低刚度，以满足隔振带宽的需要。然而，这也导致了隔振系统静支撑能力不足，位移响应增大。基于以上原因，在过去二十年间，利用非线性特征拓宽隔振带宽得到广泛关注和深入研究。例如，Carrella等[10]利用两个斜拉弹簧和竖直弹簧构建了一种准零刚度隔振器，极大的提高了隔振带宽。严博等[11]利用永磁体构建了等效负刚度，实现了大幅值激励下的高性能隔振。杨凯等[12]提出了适用于空间环境的非线性消振器结构，实现了空间环境下航天器结构的振动抑制。目前研究较多的是“三弹簧”结构[13]和一些基于永磁结构的非线性隔振[14-16]。此外，还可以根据仿生构型实现高静刚度低动刚度隔振，如剪刀型结构[17]，滚球型结构[18]， X形结构[19]，仿骨架结构[20]。但由于强非线性，系统可能产生混沌及跳跃现象，会影响隔振性能[21]。

传统的线性/非线性隔振器通过增加质量、减小刚度或者引入非线性等方法来拓宽隔振带宽。杠杆结构可通过杠杆效应放大质量-弹簧组合来产生反共振频率[22-23]。当通过杠杆放大的质量产生的惯性力抵消弹簧力时，会出现反共振。基于此，将杠杆与传统线性隔振器结合，用产生的惯性力增大隔振器的质量，从而增大了隔振带宽。Yilmaz等[24]根据杠杆支点位置设计了两种杠杆式反共振隔振器，并进行了理论建模。随后Yilmaz等[25]又讨论了多杠杆型反共振隔振器，可实现单自由度系统的最低阻带频率。Liu等[26]将混合杠杆嵌入一个X形结构中，结果表明，该系统可在多频和随机激励下有很好的隔振性能，并且对低频区被动隔振系统的设计有一定的指导意义。Zang等[27]将杠杆系统加入到非线性能量阱中，结果表明，杠杆型非线性能量阱在具有相同质量、阻尼和非线性刚度情况下性能优于常规非线性能量阱。Yang等[28]研究了杠杆与双稳态耦合非线性能量收集器，该装置可提高能量回收性能。

以上研究表明，有效利用杠杆结构可以提高隔振器的隔振性能与隔振带宽。相比于传统拓宽隔振带宽的方法，杠杆结构具有结构简单，效果可调，易于加工等优点。本文设计了一种新型杠杆式隔振器，将杠杆结构与隔振器结合，通过杠杆结构来提高隔振性能与隔振带宽，并通过研究杠杆自由端质量、杠杆比以及非线性阻尼对隔振器隔振性能和隔振带宽的影响进一步揭示了杠杆式隔振器的隔振性能。

1 新型杠杆式隔振器结构

图1为杠杆式隔振器的3D模型，包括杠杆子结构和质量-弹簧-阻尼单元。杠杆子结构通过转动副与负载板相连，杠杆自由端为一大小可调节的配重，中间铰支座固定在基板上。杠杆可绕转动支点转动，通过调节连杆的位置调节杠杆比。在轴向使用了4个直线轴承以减小摩擦带来的影响。

图1 杠杆式隔振器3D模型Fig.1 Three-dimensional model of lever-type vibration isolator

2 杠杆式隔振器的理论模型

图2为杠杆式隔振器的简化模型。图2中：mu，mb和ml分别为负载板、杠杆自由端配重及杠杆的质量；k为四个线性弹簧刚度的总和；c为系统的等效黏性阻尼；l1和l2分别为负载板支点和质量块到杠杆转动支点O的水平距离。与螺旋弹簧相比，杠杆的刚度足够大，因此，本文忽略了杠杆的弹性变形和转动带来的影响。由图2可知，杠杆自由端配重的位移zb和负载板的位移z满足

zb=-αz

(1)

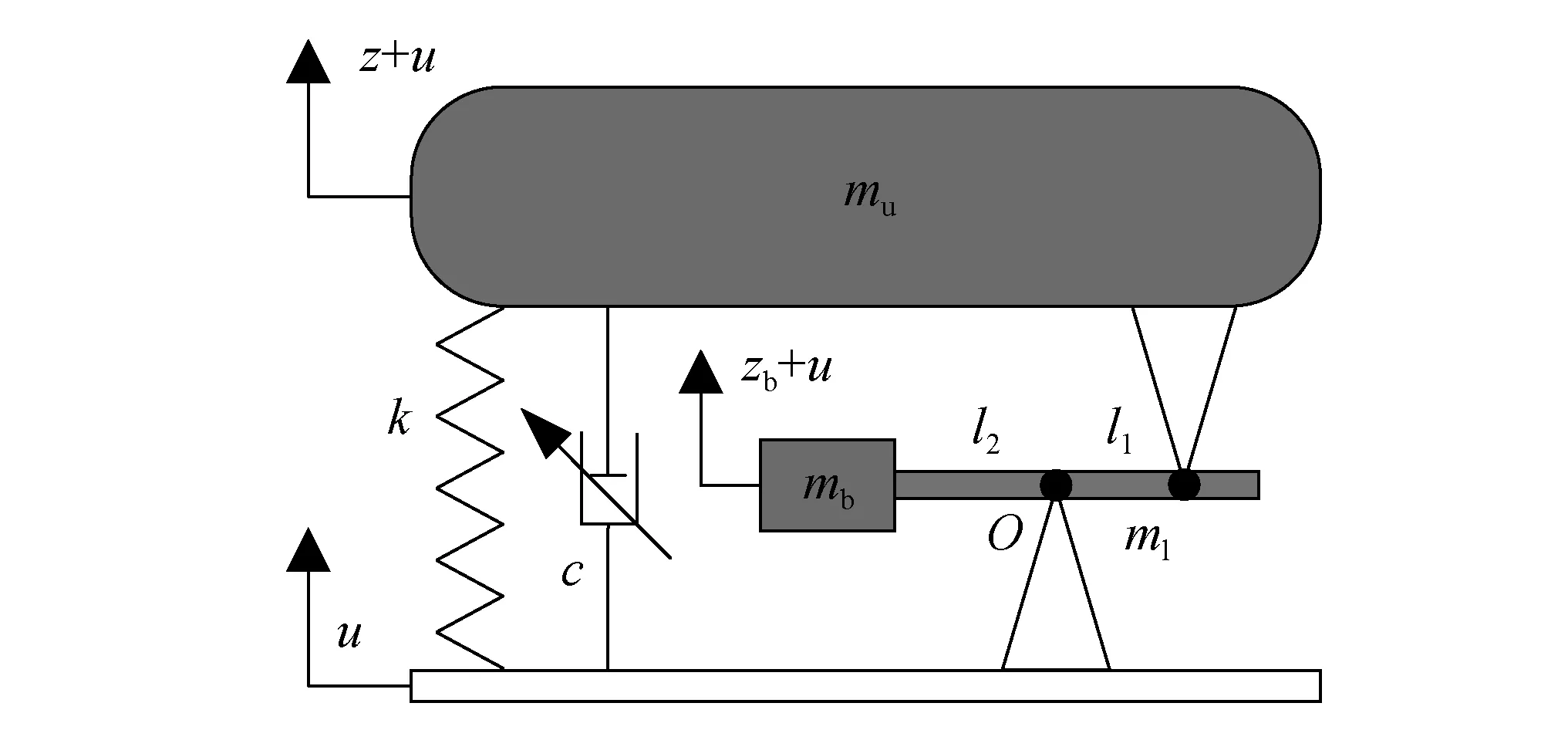
图2 杠杆式隔振器简化模型Fig.2 Simplified model of lever-type vibration isolator

假设隔振器受到u=U0sin(ωt+θ)的基础加速度激励。其中：U0为激励幅值；ω为激励频率。系统的动能为

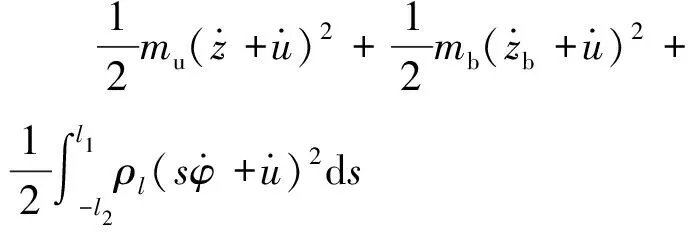
(2)

记ρl为单位长度的杠杆质量，则杠杆的质量为

ml=ρll1(1+α)

(3)

考虑到杠杆的转动角度φ=z/l1较小，将式(1)和式(3)代入式(2)，可得

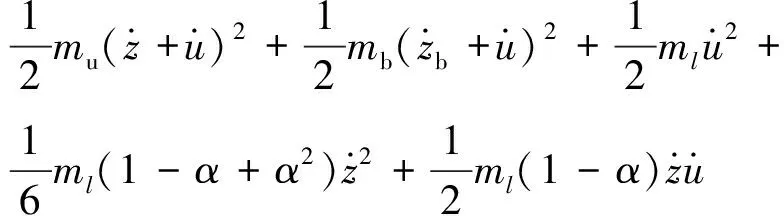
(4)

系统的势能和非保守力所做的虚功分别为

式中,K是关于参数θc的协方差矩阵,[K]i,j=k(xi,xj)θc,N(z|μ,Σ)表示向量z服从均值为μ,方差为Σ的标准正态分布。

(5)

(6)

因此，根据拉格朗日方程

(7)

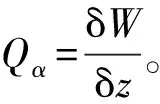
(8)

记

(9)

(10)

式中，M和m分别为惯性耦合项和激励耦合项，则式(8)可以简化为

(11)

等式(11)中包括非线性项，可以用谐波平衡法进行求解，设方程的解

z=asin(ωt)+bcos(ωt)

(12)

将等式(12)代入等式(11),忽略高次谐波，可得

(13)

式中，r2=a2+b2。

从中可得

(14)

(15)

则隔振器的总位移为

x=z+u=

u0cos(ωt+θ)+rcos(ωt)

(16)

根据传递关系，可知系统的位移传递函数为

(17)

3 数值仿真

本节着重探讨杠杆自由端配重mb、杠杆比α及非线性阻尼对杠杆式隔振器隔振性能的影响规律。表1为杠杆式隔振器参数，基于理论建模结果可计算传递率，其中，等效阻尼可由试验结果并根据半功率法获得。

表1 杠杆式隔振器的参数

图3为当α=1时的位移传递率曲线对比图，未控制曲线是指隔振器未安装杠杆子结构，则隔振器为传统的线性隔振器。mb=0是指隔振器的杠杆子结构未安装配重。可以看出，通过引入杠杆子结构隔振器的传递率降低，峰值频率左移。当mb=0.083 kg时，相比于未控制的传递率16.7和固有频率7.97，传递率和固有频率分别降低到了10.84和6.97，隔振性能提高了35.1%，固有频率下降了12.5%。可以看出，杠杆式隔振器体现出了良好的隔振特性。图中阴影面积及之后代表隔振带，当有附加质量mb时，起始点逐渐前移，可以看出系统出现了反共振频率，拓宽了隔振器的隔振带宽。

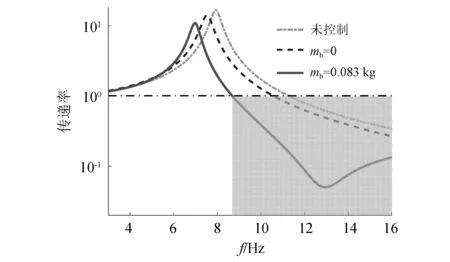
图3 当α=1时的位移传递率曲线Fig.3 Displacement transmissibility curve when α=1

3.1 杠杆自由端配重mb

图4为惯性耦合项和激励耦合项随mb变化的曲线图。图5为当α=1时mb对隔振器传递率的影响曲线图。由式(8)～式(11)可知，mb影响系统的惯性耦合项，从而改变系统的传递率，随着mb的增大，系统的峰值频率和传递率减小。由图4和图5也可以看出，随着mb的增大，惯性耦合项M缓慢增大，激励耦合项m逐渐下降；而系统的峰值频率前移，传递率减小。因此，在一定范围内可通过适当增大mb来提高隔振性能与隔振带宽。

图4 质量随mb变化的曲线图Fig.4 Variation of mass with respect to mb

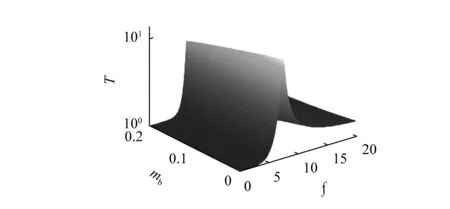
图5 当α=1时不同mb下的传递率曲线Fig.5 Transmissibility under different mb when α=1

3.2 杠杆比α

图6为惯性耦合项和激励耦合项随α变化的曲线图。图7为当mb=0.083 kg时mb对隔振器传递率的影响曲线图。由式(8)～式(11)可知，改变α同样可以改变系统的惯性耦合项与激励耦合项，从而改变隔振器的传递率。由图6和图7可知，与改变mb相反，惯性耦合项M比激励耦合项m变化更剧烈。杠杆子结构可以降低传递率，此外，随着α的增大，固有频率逐渐左移。传统的线性隔振器要达到这样的效果只能通过增大质量或降低刚度的方式来实现，准零刚度隔振器则需要引入非线性。然而，本文提出的杠杆式隔振器仅需通过调节杠杆比即可达到所需的隔振性能。

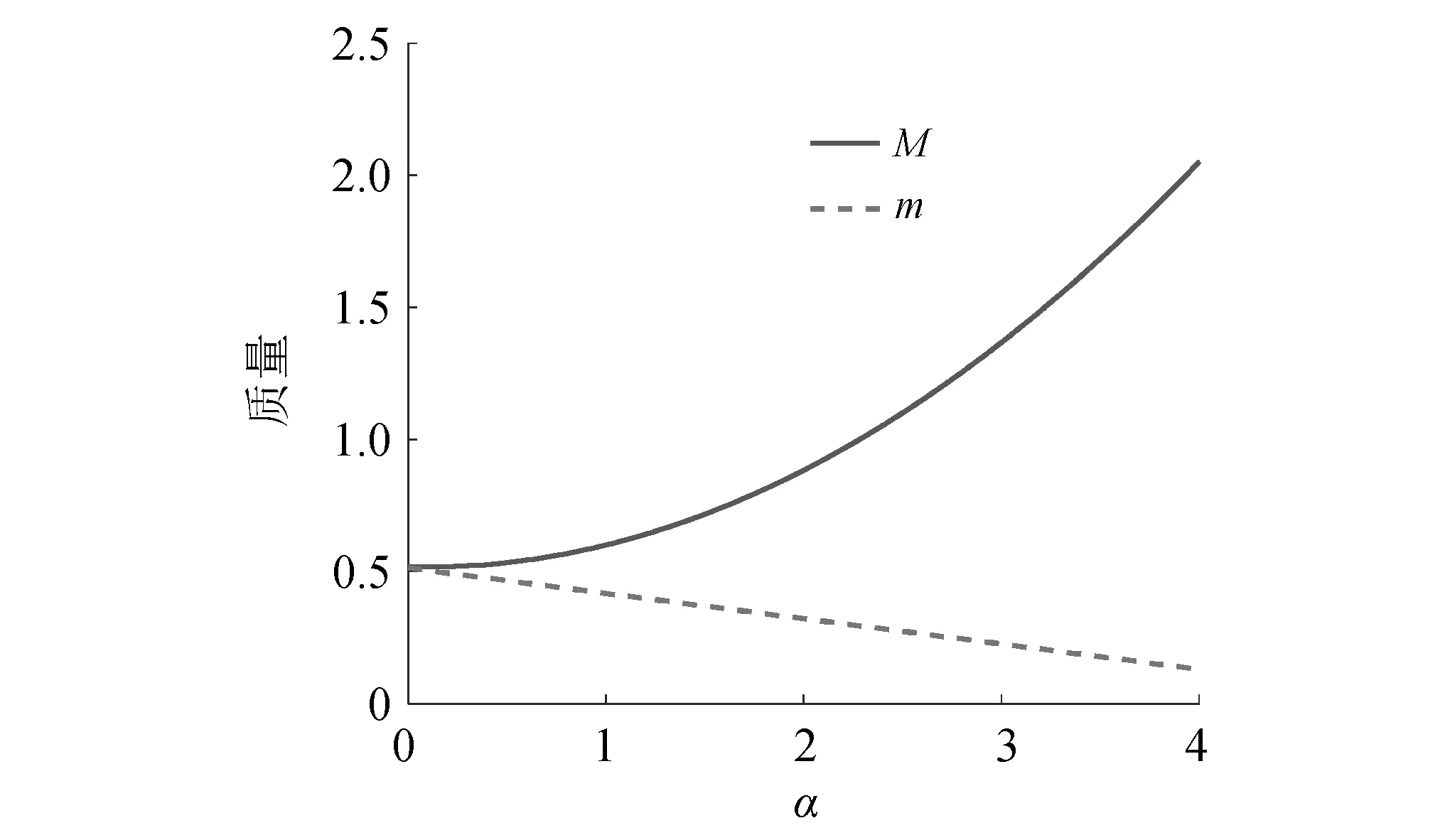
图6 质量随α变化的曲线图Fig.6 Variationof mass with respect to α

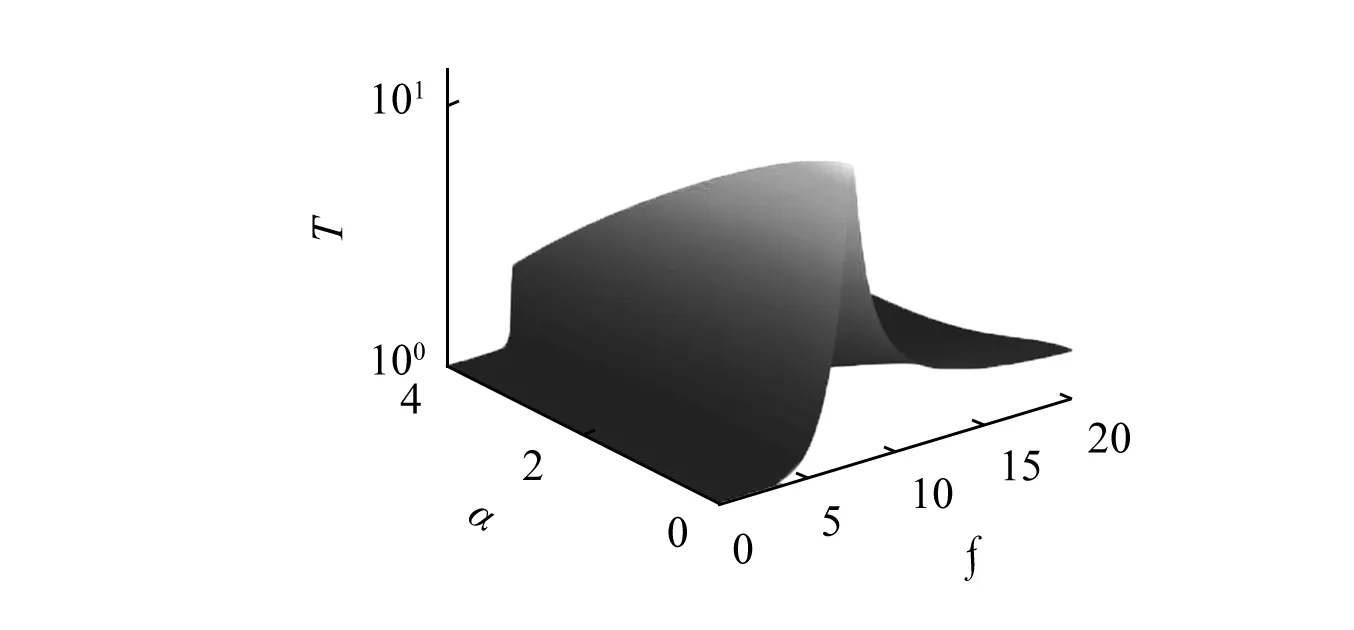
图7 当mb=0.083 kg时不同杠杆比α下的传递率Fig.7 Transmissibility with respect to the lever ratio α when mb=0.083 kg

3.3 非线性阻尼

图8为隔振器传递率随c0变化的曲线。由式(11)可知，改变c0可以影响阻尼系数。随着c0增大，隔振系统的传递率不断降低而峰值频率和反共振频率不变。相比于c0的变化，杠杆比与末端质量的变化会更有利于减振。

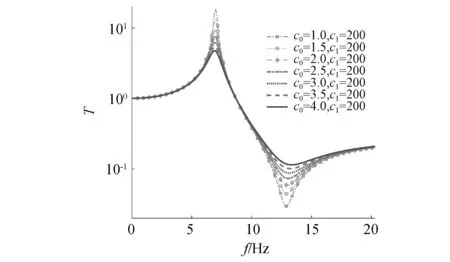
图8 不同c0下的传递率Fig.8 Transmissibility under different c0

图9为阻尼系数随c1变化的曲线。图10为隔振器传递率随c1变化的曲线。由图中可以看出，阻尼系数会随着c1的变化发生巨大的变化。但是随着c1不断增大，系统的传递率会发生较小的降低，该变化与c0的变化相比可以忽略不计。

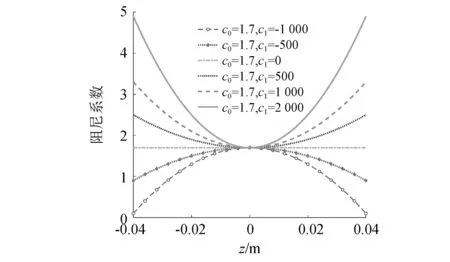
图9 不同c1下的阻尼系数Fig.9 Damping coefficient under different c1

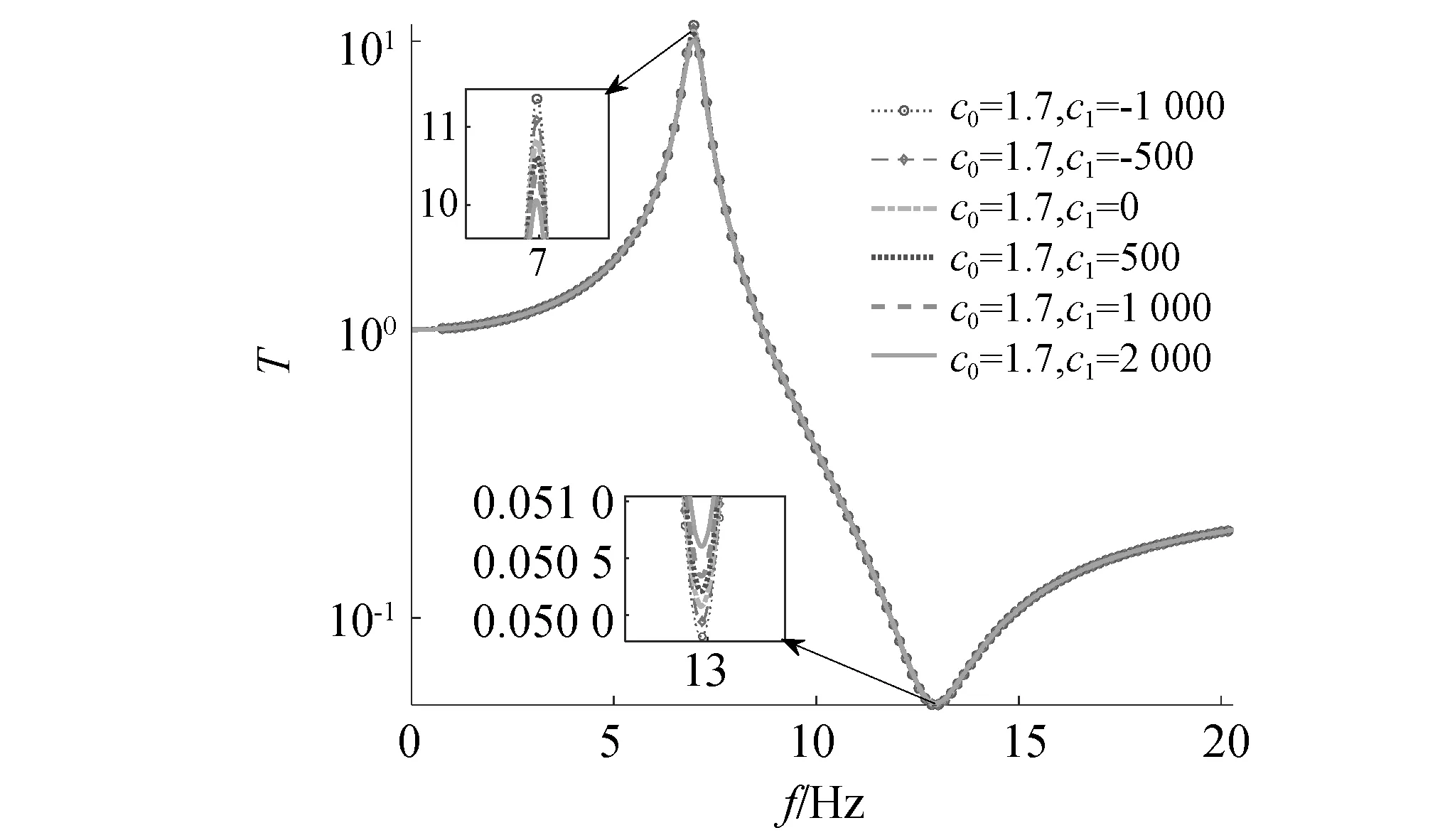
图10 不同c1下的传递率Fig.10 Displacement under different c1

4 试验设计与讨论

4.1 试验系统设计

图11为杠杆式隔振器原理样机。图12为试验装置及隔振器的照片，其中，杠杆式隔振器的基板固定在激振器。试验系统由控制器、功率放大器、激振器、计算机以及两个加速度传感器组成。信号发生器产生正弦激励信号经控制器传递至功率放大器，驱动激振器。其中，使用两个加速度传感器测试隔振器和激励响应，通过两个加速度传感器可得到隔振器的传递率。试验扫频速率为1 Hz/s，其他试验参数见表1。

图11 杠杆式隔振器原理样机Fig.11 Prototype of the lever-type vibration isolator

图12 试验装置照片Fig.12 Photograph of experiment setup

4.2 试验结果

图13为测试而来的传递率曲线，可知，未控制情况下，隔振器的最大位移传递率(T)和峰值频率(fn)分别为15.81和7.87 Hz。加入杠杆子结构后，最大位移传递率降低到13.62，峰值频率降低到7.60 Hz。在杠杆末端加上质量块后，最大位移传递率降低到11.15，隔振效果提高29%，峰值频率降低到6.98 Hz，峰值频率降低11%。试验结果验证了杠杆结构可以提高隔振带宽，并具有良好的隔振性能。

图13 试验传递率曲线Fig.13 Experimental transmissibility curve

4.2.1 不同mb下的隔振性能

图14为当α=1.5时不同mb下的试验传递率曲线，可知，mb=0.126 kg时隔振器的最大位移传递率和峰值频率分别为5.98和6.03 Hz，相比于mb=0，共振峰值下降了44%，固有频率降低20%。此外，试验结果也证明了随着mb的增大，固有频率和最大传递率逐渐减小，即隔振带宽和隔振效果均有所提高，但是，mb的增大也会使隔振器变得笨重，所以应合理选择mb。

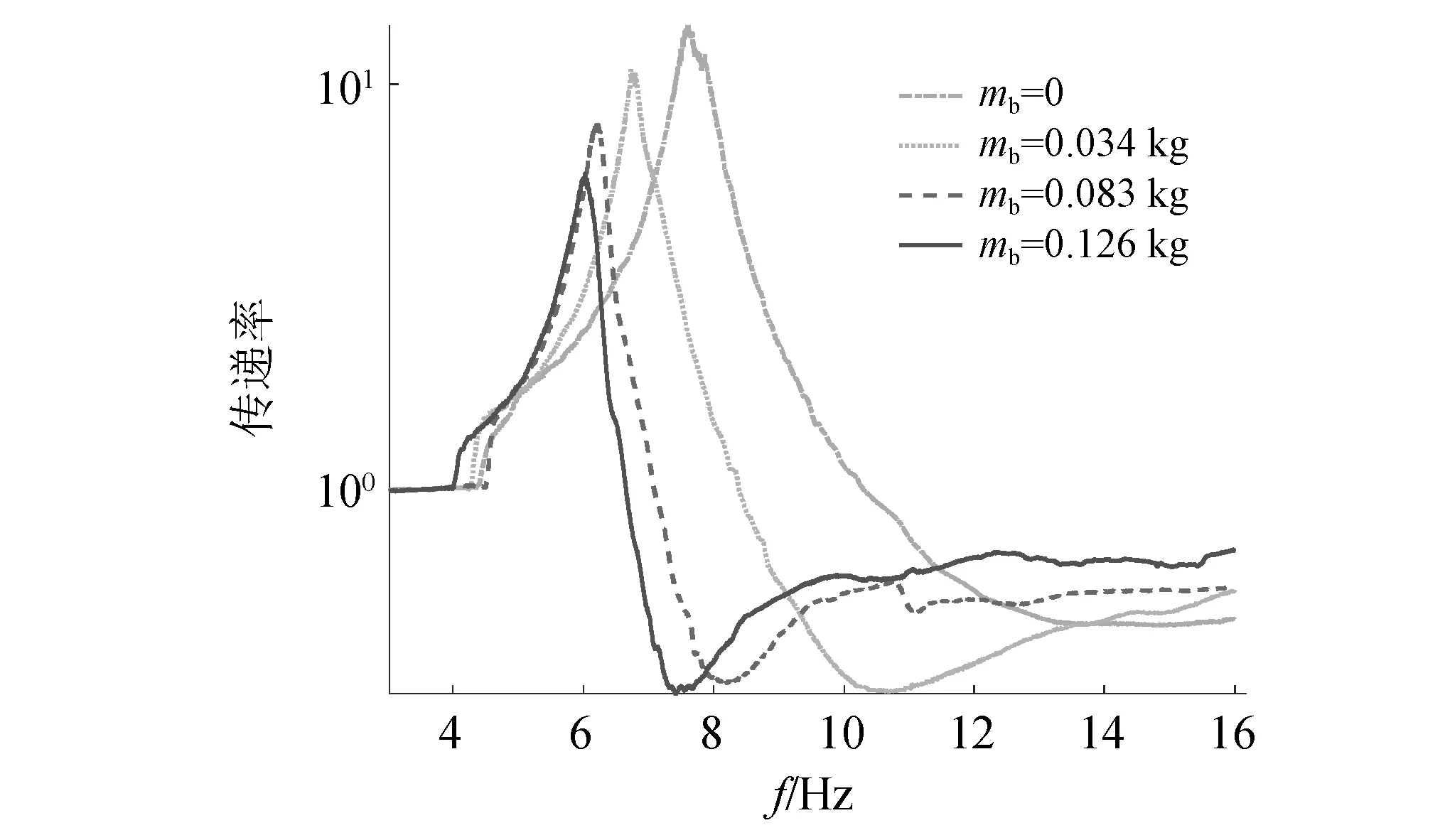
图14 当α=1.5时不同mb下的试验传递率曲线Fig.14 Experimental transmissibility under different mbwhen α=1.5

4.2.2 不同α下的隔振性能

图15为当mb=0.083 kg时不同α下的试验传递率曲线，可知，随着α的增大，隔振器的最大位移传递率和共振频率分别从α=0.75时的11.76和7.24 Hz减小到α=1.50时7.97和6.21 Hz，共振峰值下降了32%，固有频率降低14%。试验结果也验证了通过改变杠杆比α可以轻松地调节隔振器的隔振性能与隔振带宽，本研究也提供了一种有异于传统线性或非线性隔振器中提高隔振效果的方法。

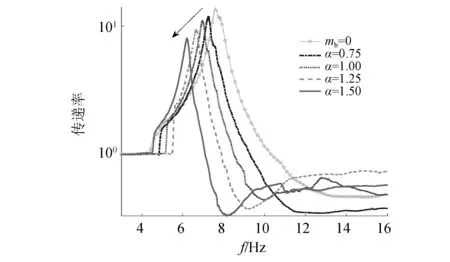
图15 当mb=0.083 kg时不同α下的试验传递率曲线Fig.15 Experimental transmissibility under different α when mb=0.083 kg

5 结 论

(1)本文设计了一种新型杠杆式隔振器，由杠杆子结构和质量-弹簧-阻尼单元组成。建立了杠杆式隔振器的理论模型，基于拉格朗日方程得到了其运动微分方程，推导了位移传递率表达式。

(2)研究了杠杆自由端配重、杠杆比及非线性阻尼对隔振器隔振特性的影响规律，基于此，研制了一种杠杆式隔振器原理样机，开展了数值分析及试验研究。

(3)研究结果表明，增大杠杆自由端配重可有效的降低系统固有频率和共振峰，随着杠杆比的增大，系统隔振带宽及隔振性能会进一步的提高。增大杠杆横截面积对隔振器隔振性能影响较小。增大阻尼可有效地降低隔振器传递率。本研究对设计和使用杠杆式隔振器均具有极强的指导意义和参考价值。