基于模糊控制的车速跟随变量喷雾系统设计与试验

王润涛 刘 瑶 王树文 李 明 孙文峰 薛 忠

(1.岭南师范学院电子与电气工程学院，湛江 524048；2.东北农业大学工程学院，哈尔滨 150030；3.中国热带农业科学院南亚热带作物研究所，湛江 524091)

0 引言

精准施药技术可有效提高农药、水肥利用率，降低环境污染程度，促进有机绿色农业发展。变量喷雾是精准施药技术的重要手段之一，通过探测技术感知环境信息作为依据，利用控制技术驱动施药装备实施变量喷雾[1-2]。实际田间作业过程中，地貌的变化对农机车体速度影响较大，如果采用恒量喷雾，车体非匀速运动状态会造成重喷、漏喷现象。

欧美国家在变量喷雾研究领域进行了大量研究，已取得重大突破[3-5]，其成果基本满足了精准施药的要求。近年，国内专家学者对变量喷雾技术从不同角度展开深入的研究[6-10]，主要侧重于以作物信息检测为依据的对靶式变量喷雾和以喷雾设备运行状态为依据的校正式变量喷雾。对靶式变量喷雾适用于果园类小区块作业，通过获取果树位置作为标靶、获取冠层面积作为喷雾流量调节依据[11]。闫成功等[12]利用双目视觉技术探测葡萄叶幕深度并结合施药机前进速度计算冠层体积从而实现变量喷雾，但研究中未考虑车速对喷雾量的直接影响。在大田宽幅喷雾作业中，研究者多侧重考虑喷雾机自身校正式变量喷雾。王相友等[13]设计了多回流式变量喷雾控制系统，根据施药机行驶速度建立PID控制模型调节比例控制阀，通过改变回流口的开口度来改变喷雾流量；孙睿等[14]设计了一种基于PID模糊控制理论的压力调控变量喷雾系统，建立了以载体农机动态速度为输入变量、控制阀驱动电压为输出变量的模糊控制规则，但系统稳定性较低；孙文峰等[15]依据监测车速、流量等信息，利用神经网络修正PID控制参数，提高了大田单位面积内恒定施药量精度。上述研究为变量喷雾提供了新思路，但在抑制农机扰动、系统延时响应、稳态跟踪效果等方面有待改进。

基于上述研究现状，为提高变量喷雾系统的抗扰性与实用性，拟设计一种能够适应农机行进速度变化的变量喷雾系统，以农机实时速度为自变量、比例阀驱动电压为控制变量、阀门变化角度为调控对象，构建车速、流量、电压的非线性模糊控制模型，降低系统的滞后性影响，从而实现出水管流量的动态实时调节，并进行田间试验，验证喷雾系统有效性和稳定性。

1 系统整体设计

1.1 系统结构设计

喷雾系统结构如图1所示，速度传感器设置于载体农机的车轮主轴外侧，流量传感器与压力传感器均安装于出水管主管路，液位传感器设置在药箱底部，控制器安装于载体农机的中控台。

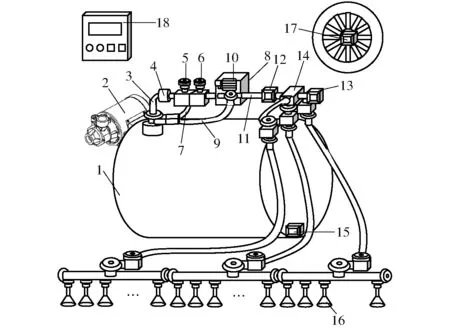
图1 喷雾系统结构示意图Fig.1 Schematic of spray system structure1.药箱 2.隔膜泵 3.进水管 4.过滤器 5.主阀 6.溢流阀 7.回流管A 8.比例阀 9.回流管B 10.直流电机 11.出水管 12.流量传感器 13.压力传感器 14.分水阀 15.液位传感器 16.喷嘴 17.速度传感器 18.控制器

喷雾系统工作过程为：连接动力输出轴与隔膜泵，启动农机，打开控制器开关，药液由隔膜泵抽送至进水管，经由过滤器滤除杂质，管路压力过大时溢流阀开启，通过回流管A使部分药液回流至药箱，防止水管破裂。比例阀是系统实现变量喷雾的关键部件，控制器依据传感器实时获取的车轮速度、出水管流量与压力、药箱液位数据，动态控制比例阀内置直流电机的电压，从而驱动阀门动作，改变阀门角度，由回流管B卸荷，间接调节出水管压力与流量，再经分水阀分配至各个支路。

1.2 控制系统设计

车速跟随变量喷雾系统电控部分由预警监测、变速监测、核心控制、执行模块4部分组成，如图2所示。

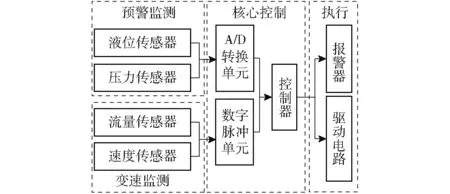
图2 喷雾系统电控原理框图Fig.2 Block diagram of electrical control principle of spray system

大田里坑洼地、田埂、坡起、明暗障碍物等随机存在，使得农机无法实现匀速前行，喷雾效果与农机车速具有显著相关性。变速监测模块包括2个传感器单元，采用NPN三线常开型SC12-20K-L齿轮转速传感器实时监测农机车轮的实际行进速度、LWGY-10型涡轮流量传感器获取管路动态流量，速度与流量信息作为调压控制的基础输入变量。

喷雾作业过程中，如果药箱内液位过低，会导致隔膜泵空抽现象，造成漏喷，为保证喷雾质量，设计预警监测模块，采用0.25级精度MIK-P310型压力传感器监测出水管压力、投入式ELE-803型液位传感器监测药箱内液位高度。设置出水管压力与药箱内液位的约束条件，如超出限定范围则通过执行模块的报警单元实现预警，并关闭比例阀阀门。

核心控制模块采用STC8A8K64S4型单片机实现数据转换、模型运算和控制命令输出。传感器获取的液位和压力信号为模拟量，经A/D转换单元传递给控制处理器，流量和车速信号为数字量，经数字脉冲单元传递给控制处理器，控制处理器进行运算，发出控制指令。通过改变H桥驱动电路开关的脉宽占空比，实现电压调节，进而调控比例阀阀门的运动位移，间接调控管路流量，完成一次调控过程。

2 车速跟随控制策略

图3 变量喷雾控制策略Fig.3 Control theory of variable spray

实际喷雾作业时，由于传感器响应速度、管道阻力等因素制约，变量喷雾控制是时变、滞后的多变量耦合非线性系统，简单的控制算法难以满足调节精度要求。

2.1 基本参数计算

设t时刻，出水管理想的需求流量为q(t)，通过速度传感器获取的实时车速计算需求流量，计算式为

(1)

式中Q——单位面积喷雾量，L/hm2

v′(t)——t时刻车速，km/h

W——喷嘴间距，cm

m——喷头数量

设t时刻，通过流量传感器测得出水管当前流量为q′(t)，q′(t)由比例阀阀门开启角和速度决定，通过控制比例阀内置电机的驱动电压调节其转速，进而控制阀门角度变化，单位时间阀门变化角度为

Δα(t)=2πΔnk

(2)

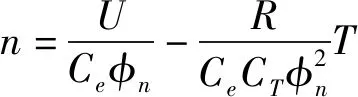
(3)

式中n——电机转速，r/min

U——电机电压，V

Ce——电动势常数

CT——转矩常数

φn——额定磁通量，Wb

T——转矩，N·mR——电枢内阻，Ω

Δn——单位时间电机转速变化量

k——比例阀齿轮比

解决控制系统响应滞后问题，即通过调节Δα(t)，使q(t)与q′(t)的偏差减小。

2.2 系统控制策略

变量喷雾系统中，比例阀输出流量具有振荡特性，基于PID的控制算法，难以实现根据受控对象的变化对参数进行准确调整，模糊控制模拟人类思维的模糊推理，不依赖于调节参数，可通过改变模糊控制规则调节系统特性，减少处理器的运算负荷，能够适应嵌入式实时系统的非线性控制问题[16-19]。本文采用模糊控制算法建立变量喷雾控制策略，如图3所示。

模糊控制器的输入为q(t)，通过设定的Q与t时刻的车速v′(t)进行运算得出。

由于地貌等因素干扰导致速度传感器实测的v(t)具有不确定性，如直接运算难以满足调节精度。为降低机械及传输滞后对控制参数的影响，首先对v(t)进行一阶微分与加权求和运算

v′(t)=v(t)+a(v(t)-v(t-1))

(4)

式中a——加权系数

将v′(t)代入式(1)，计算得出q(t)，与流量传感器采集的q′(t)进行偏差运算

(5)

式中E(t)——偏差，L/min

EC(t)——偏差变化率，L/min2

如果E(t)=0、EC(t)=0，即农机实际行进速度无变化，不启动控制模块。如果E(t)与EC(t)不为0，进行模糊运算，得出比例阀电机驱动电压U(t)，由式(2)计算得出Δα(t)，调节后出水管流量发生改变，q′(t)作为输出，并反馈至输入端与q(t)进行比较运算。控制过程中，另设并行支路实现出水管压力与药箱液位的超限预警。预警约束条件为P(t)>0.2 MPa，H(t)>30 mm。P(t)为t时刻出水管压力，H(t)为t时刻药箱液位高度。

如果信号不满足约束条件，启动报警器报警，同时U(t)反向增大至比例阀阀门关闭，切断出水管药液供给。

3 模糊控制模型

3.1 模糊控制算法实现

系统的受控对象为比例阀阀门开度，其控制响应存在滞后性，传递函数采用一阶惯性加纯滞后函数，依据系统辨识理论中的近似法结合试验分析[20]，估测传递函数为

(6)

利用Matlab仿真软件建立算法仿真模型，如图4所示。

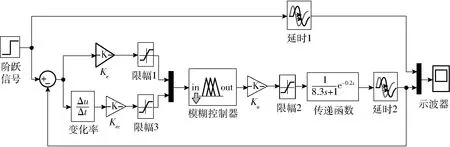
图4 控制算法仿真模型Fig.4 Simulation model of control algorithm

图4中，Ku为模糊控制器输出的比例因子、Ke为E(t)的量化因子；Kec为EC(t)的量化因子，通过设定限幅使输入与输出稳定在允许范围内。为简化运算，用“模糊数”替代“模糊子集”，采用7个模糊数{-3、-2、-1、0、1、2、3}，分别表示{负大、负中、负小、零、正小、正中、正大}。U(t)的输出规则计算公式为

U(t)=βE(t)+(1-β)EC(t) (β∈[0,1])

(7)

式中β——E(t)模糊数的权重

只考虑模糊控制器的输出对系统的影响，设Ku、Ke、Kec的值为1，E(t)、EC(t)和U(t)所有模糊子集采用等腰三角形函数，均分在对应的论域。采用Bisector去模糊化算法，模糊逻辑与运算、蕴涵运算取最小值，或运算、综合运算取最大值。通过设置β的不同取值，寻求最优规则。设β以0.1为步长，从0.2递增至0.8，阶跃响应仿真曲线如图5所示。

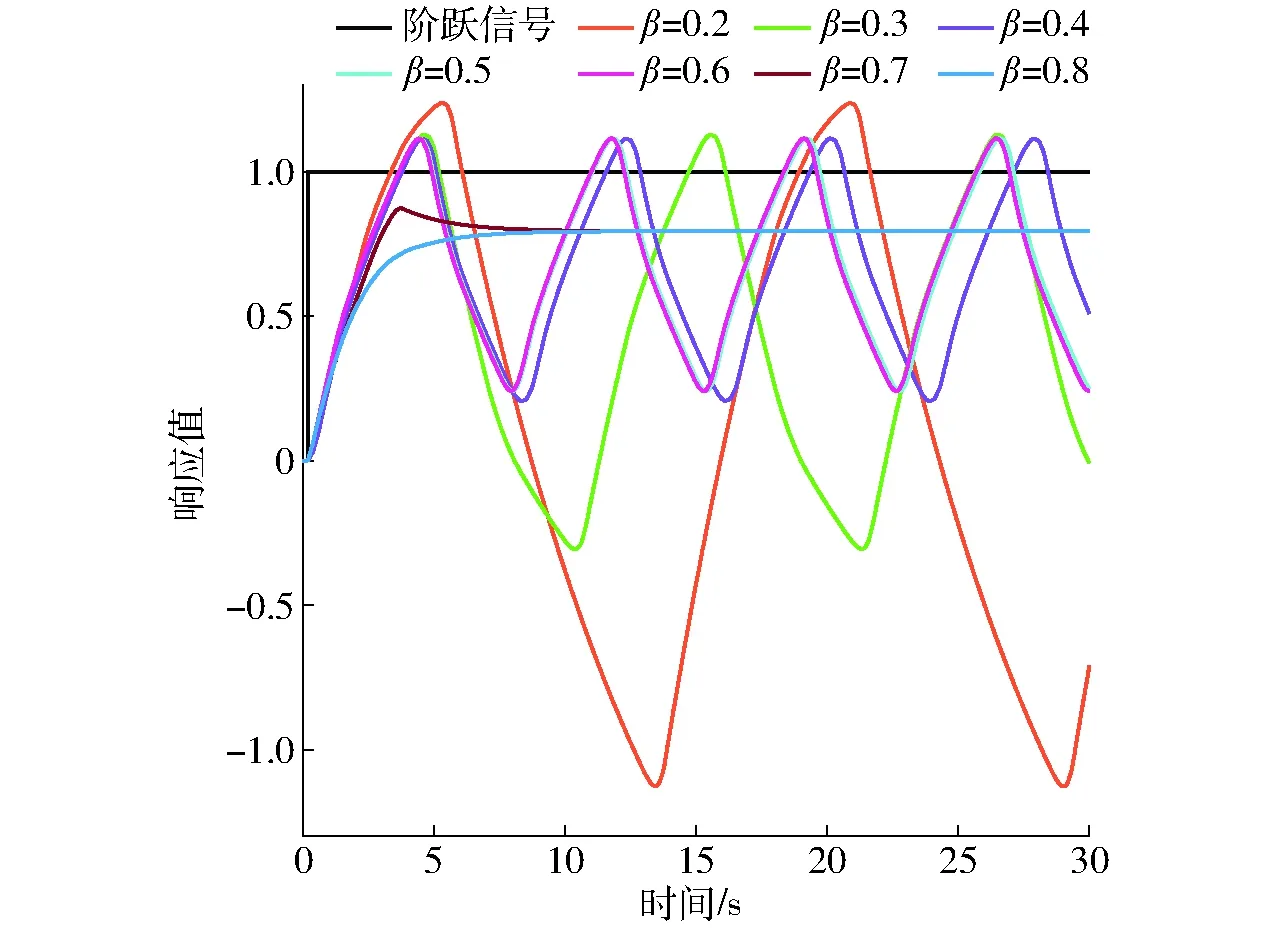
图5 阶跃响应曲线Fig.5 Curves of step response

由图5可知，7种模糊规则中，β=0.7、β=0.8响应曲线呈现较为显著的收敛趋势，当输入信号发生跃变时，β=0.7响应速度最快，且能够快速恢复至稳定状态。取β=0.7建立模糊规则，对应模糊数见表1。

图5中β=0.7响应曲线虽然相对优越，但其稳态误差较大。为进一步优化该模型的性能指标，经过反复试验，选取Ku=1.3、Ke=1.8、Kec=0.5，调节E(t)模糊子集取值范围，结果见表2。

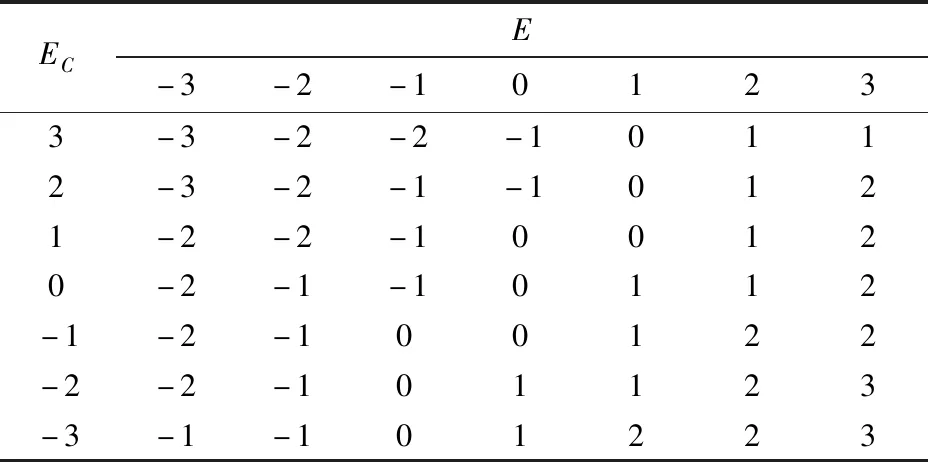
表1 模糊控制规则Tab.1 Fuzzy control rule

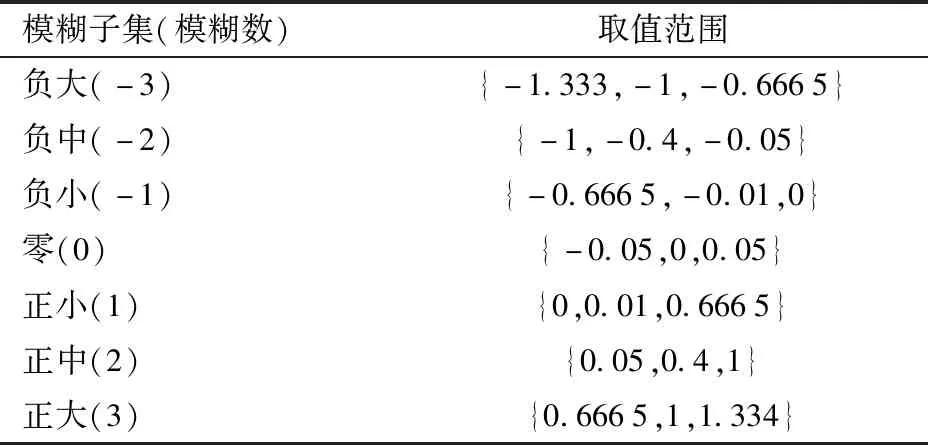
表2 E(t)模糊子集最优取值Tab.2 Optimal value of E(t) fuzzy subset

3.2 控制算法分析

为验证上述Bisector模糊控制算法应用于变量喷雾系统的鲁棒性与优越性，与PID控制算法、Centroid模糊控制算法进行仿真对比试验[21-22]。

传递函数采用式(6)，依据Ziegler-Nichols(Z-N)参数整定方法，PID控制器的Kp、Ki、Kd分别取值3.8、3.2、0.76。Centroid模糊控制算法采用3.1节得出的模糊规则与最优参数取值。阶跃响应曲线对比如图6所示，性能指标对比见表3。

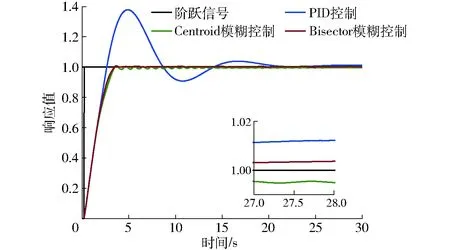
图6 阶跃响应对比曲线Fig.6 Curves of step response comparison

由图6与表3可知，Bisector模糊控制算法在上升时间、调节时间、超调量与稳态误差方面均优于Centroid模糊控制算法。PID控制算法的上升时间最短，但超调量与稳态误差较大。考虑Bisector模糊控制算法虽然上升时间比PID控制算法滞后0.75 s，但PID超调过大，需要20.74 s调节至稳态，导致系统跟随响应滞后。本文的变量喷雾系统为非线性、时变系统，传递函数无法进行准确预测，而PID控制算法的性能依赖于传递函数准确性。模糊控制算法的鲁棒性强，干扰和参数变化对其控制效果影响小。综合考虑，Bisector模糊控制算法能够更好地满足本系统快速响应、动态跟踪、稳定输出的要求。

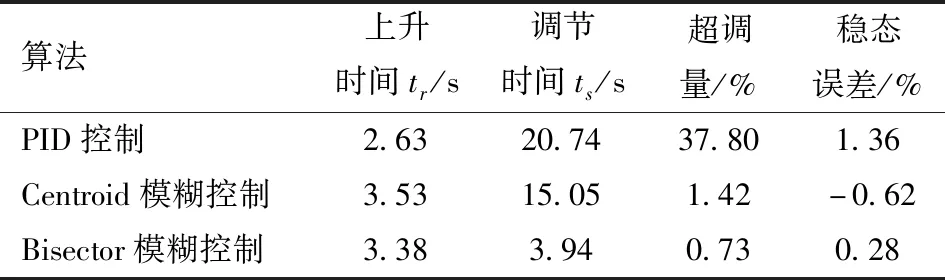
表3 阶跃响应性能指标Tab.3 Performance index of step response

4 试验

4.1 试验条件

于东北农业大学大豆实验基地进行大田试验，选择大豆生长1～3片复叶、杂草2～5叶期进行苗后除草，进行非行走设定车速、恒定车速跟随、动态车速跟随3种试验。喷雾装置采用3WF-1000型喷杆式喷雾机，配置ÖNΛLLΛR C-96型隔膜泵、AIXR11003型喷头(数量36、间距0.5 m)、幅宽18 m桁架、容量200 L药箱。载体机具采用纽荷兰110-90型拖拉机，喷雾介质为精喹禾灵水溶液。

自主设计的变量喷雾系统阀体部分与控制器如图7所示。

图7 变量喷雾系统控制主体Fig.7 Control core of variable spray system

4.2 非行走设定车速试验

为分析农机动力因素对控制系统响应速度与稳定性的影响，设置Q为150 L/hm2，保持农机怠速状态，屏蔽速度传感器，设定速度10 km/h直接输入控制系统，管路流量响应曲线如图8所示。

图8 非行走设定车速试验流量响应曲线Fig.8 Flow response curves of non-travel fixed speed test

v(t)为10 km/h恒速时，由式(1)计算得q(t)为45 L/min。t>0时，为使喷头达到雾化效果，需满足q′(t)>18 L/min；t<6.7 s时，q′(t)从18 L/min至45 L/min呈线性上升趋势，由于q′(t)与q(t)初始差值较大，模糊控制规则输出取正大，q′(t)以最大速率上升，逼近q(t)；6.7 s≤t<9.8 s时，由于机械惯性的作用，q′(t)从45 L/min至48 L/min仍缓慢上升，大于q(t)，出现超调，模糊控制规则输出取负中；9.8 s≤t<13.4 s时，q′(t)从48 L/min至45 L/min呈下降状态，通过模糊控制模型进行偏差调节，稳定输出量；t≥13.4 s时，q′(t)以45 L/min稳定输出。非行走设定车速试验实测单位面积喷雾量约为151.6 L/hm2，与设定值相差1.1%。

4.3 恒定车速跟随试验

为验证农机从启动至行进过程中，喷雾系统适应扰动、跟随车速的效果，选择平坦试验区域，启动速度传感器，驾驶员控制农机以速度10 km/h匀速行驶，控制系统依据实时车速进行动态调节。实时车速曲线如图9所示。

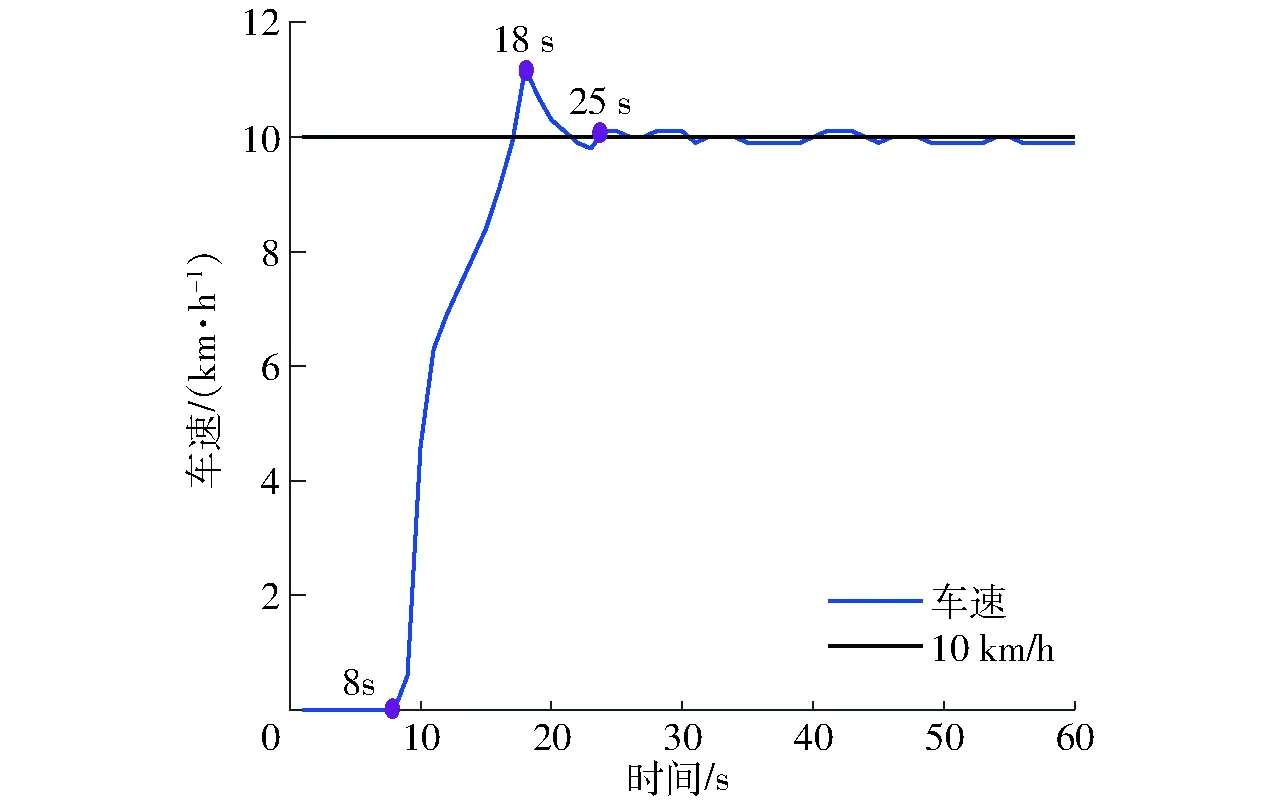
图9 恒定车速跟随试验车速变化曲线Fig.9 Speed curve of fixed speed following test

试验过程中，由于农机启动系统、驾驶员主观操作因素的影响，行进速度不能保持恒定。5 s≤t<8 s时，由于农机自身启动延时，v(t)为0；8 s≤t<18 s时，v(t)迅速增大至11.2 km/h，由于惯性出现超调现象；t≥25 s时，v(t)趋于稳定。农机从启动到稳定行驶耗时25 s。

管路流量跟随车速的变化曲线如图10所示。由图10可知，5 s≤t<8 s时，q(t)由v(t)计算出为0，驾驶员启动农机瞬间，轴动力输出减小，造成隔膜泵动能降低，使得q′(t)减小，启动控制系统调节；8 s≤t<16.5 s时，q(t)随v(t)增大，q′(t)也随之递增至45 L/min；16.5 s≤t<18.8 s时，q(t)与q′(t)出现超调现象；经系统调节后，t≥27.6 s，系统基本达到稳定状态，q′(t)曲线与q(t)曲线逼近。恒定车速跟随试验实测单位面积喷雾量为153.2 L/hm2，与理论值相差2.1%。

图10 恒定车速跟随试验流量响应曲线Fig.10 Flow response curves of fixed speed following test

4.4 动态车速跟随试验

大田作业环境，农机行进过程中遇到坑洼、土坡等会造成车速波动。为进一步验证喷雾系统的准确性与鲁棒性，选择大豆垄田试验区域，由驾驶员根据实际情况动态控制车速。动态变化车速曲线如图11所示。

图11 动态车速跟随试验车速变化曲线Fig.11 Speed curve of dynamic speed following test

4 s≤t<17 s，为农机系统启动耗时；t=37 s、t=92 s、t=112 s时加速行进，t=63 s、t=138 s时减速行进。

管路流量跟随车速的动态变化曲线如图12所示。4 s≤t<17 s，农机系统启动、喷雾系统进行相应调节，q(t)与q′(t)变化趋势与恒定车速跟随试验一致；t≥17 s时，随着车速动态变化，无论加速点还是减速点，当前流量与需求流量的曲线均能较好的拟合，说明经过控制系统的调节，q′(t)能够跟随q(t)的动态变化而变化，并且保持较小的偏差，实现动态跟随目的。动态车速跟随试验实测单位面积喷雾量为154.1 L/hm2，与理论值相差2.7%。

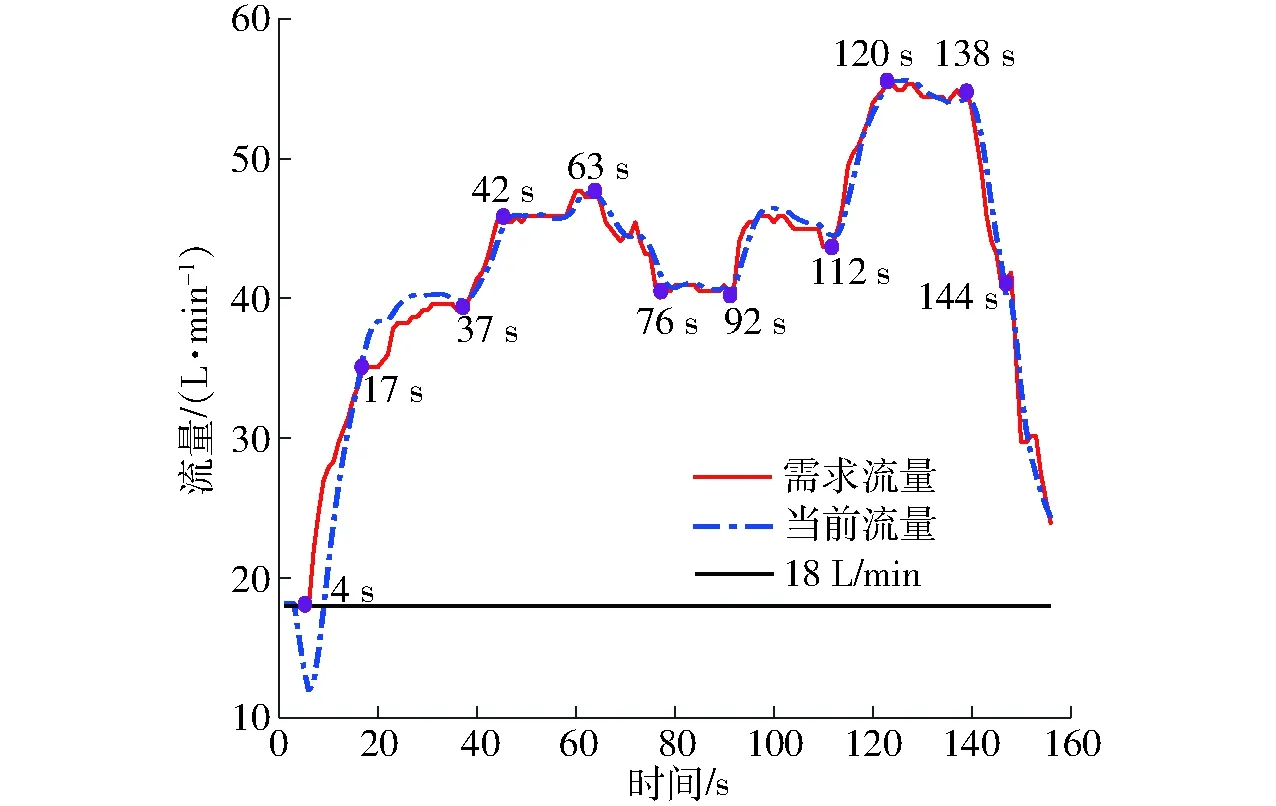
图12 动态车速跟随试验流量响应曲线Fig.12 Flow response curves of dynamic speed following test

4.5 单位面积喷雾量误差分析

喷雾系统出水管总流量为各个支路的喷嘴喷雾量之和，试验前在每个喷嘴下方放置量筒，作为实测喷雾量的标定。非行走设定车速、恒定车速跟随、动态车速跟随3种车速状态，各进行5次试验。农机车速变化范围4～12 km/h，误差数据见表4。

表4中数据显示，不同车速状态下，非行走设定车速试验、恒定车速跟随试验、动态车速跟随试验，喷雾量实测值与设定值的最大绝对误差比率分别为1.20%、2.27%、2.87%，满足实际生产需求。

5 结论

(1)针对大田宽幅机械变量喷雾精准化程度低、车速影响考虑不充分的问题，设计了基于模糊控制的车速跟随变量喷雾系统，该系统能够依据农机车速变化实时调节出水管流量、依据出水管压力与药箱液位变化动态预警，系统运行稳定。

(2)利用Matlab对7种模糊控制规则进行仿真分析，得出偏差的权重为0.7时，模糊控制模型响应速度最快，且能够快速恢复至稳定状态；对3种控制算法进行了仿真对比，结果表明，Bisector模糊控制算法的上升时间、调节时间、超调量、稳态误差分别为3.38 s、3.94 s、0.73%、0.28%，综合性能较优。

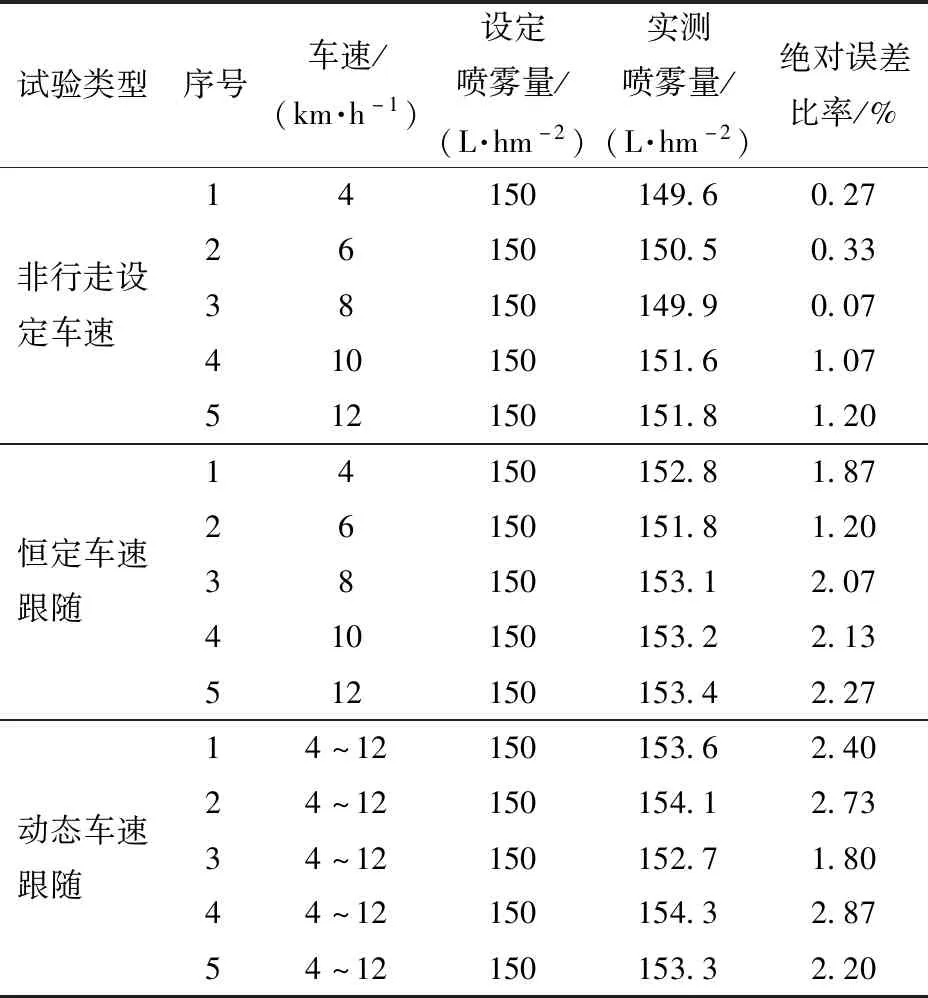
表4 单位面积喷雾量误差Tab.4 Error of spray volume per unit area

(3)车速跟随试验结果表明，非行走设定车速状态，屏蔽干扰，控制系统自身调节达到稳定，调节耗时13.4 s；恒定车速状态，受农机动力系统启速过程扰动，控制系统调节至稳态耗时27.6 s；动态车速状态，控制系统跟随农机车速实时调控，调节耗时17 s。当前流量能够稳定跟随需求流量，速度变化点动态响应效果良好。

(4)单位面积喷雾量试验结果表明，车速在4～12 km/h变化范围，非行走设定车速、恒定车速、动态车速3种状态，单位面积喷雾量最大绝对误差比率分别为1.20%、2.27%、2.87%，实现了较高精度的变量喷雾目标。