地面堆载对既有隧道影响离心试验和数值分析

2022-08-05刘谨豪严远忠叶冠林

上海交通大学学报 2022年7期

随着城市地下空间进一步开发，交通隧道、地下管线变得越来越密集，邻近既有隧道的地面堆载问题难以避免.上海市规定了地下结构设施受邻近施工影响20 mm的位移限值，但并未对隧道周边堆载规模做出细致研究和明确规定，仅仅采取禁止堆载的措施，从而导致很多临时性堆载项目受限而无法开展，影响工程项目的顺利进行.

近年来，许多学者对地面堆载导致的隧道位移问题进行了大量研究.邵华等利用现场监测数据，分析了上海某地铁区间突发堆载对隧道位移的影响，提出了加固补强措施.李卫超等分析了深厚软土大面积堆载对地基压缩层的影响，讨论了地层模量和沉降经验系数取值方法.Wang等假定地层为黏弹性材料，考虑浅埋隧道和任意位置地面堆载，提出了计算隧道变形的预测公式.梁发云等建立了层状地层地面堆载对既有隧道影响的解析算法，利用Fourier变换和两阶段法，计算了堆载引起的附加应力和隧道位移.黄大维等通过相似模型试验和理论分析，认为隧道上方附加竖向土压力会大于地面堆载，隧道所在土层越软弱，位移控制难度越大.张明告等结合缩尺模型试验和数值模拟，分析了土体压缩模量在地面堆载问题中的影响.Ali等利用随机自适应有限元分析(RAFELA)方法，考虑地层空间变异性，研究了地面堆载对隧道稳定性的影响.

现有研究中，缩尺模型试验没有考虑实际工程中土体所受的高应力，不能还原软黏土地层受堆载影响的变形发展过程.数值计算一般采用参数较少的摩尔库伦模型或修正剑桥模型，未能考虑土体刚度随应变衰减特征，使计算结果偏大.另外，已有研究多是讨论单一因素对隧道位移的影响，未能考虑堆载规模和隧道位置对隧道位移的综合影响.

本文基于上海软黏土地质条件，开展了离心模型试验，研究了地面堆载对隧道位移和土体变形的影响规律.基于离心模型试验建立相应的有限元模型，分析了小应变刚度在软土地区地面堆载问题中的适用性.在此基础上，综合考虑堆载规模和隧道位置，研究了地面堆载对下部软黏土地层变形和隧道位移的影响.

1 离心模型试验

1.1 试验仪器和材料

离心模型试验在上海交通大学DC-2200鼓式离心机内进行，如图1所示，离心机有效旋转半径为1.1 m，最大荷载为600t，即可在最大 200离心加速度下运载3 t试验物质.离心机底盘安装有无线接入点和微型电脑主机，可以实现试验数据无线交换.本试验为二维平面应变试验，模型率为100，即试验过程中离心机稳定运转时加速度为 100.试验用模型箱如图2所示，试验过程中侧立于离心机鼓室内.

（1）在水轮发电机组发生故障时，能及时、准确、自动、可靠的找出原因，并切出故障，避免机组长时间受到破坏，确保其他无故障部分迅速恢复正常运作。

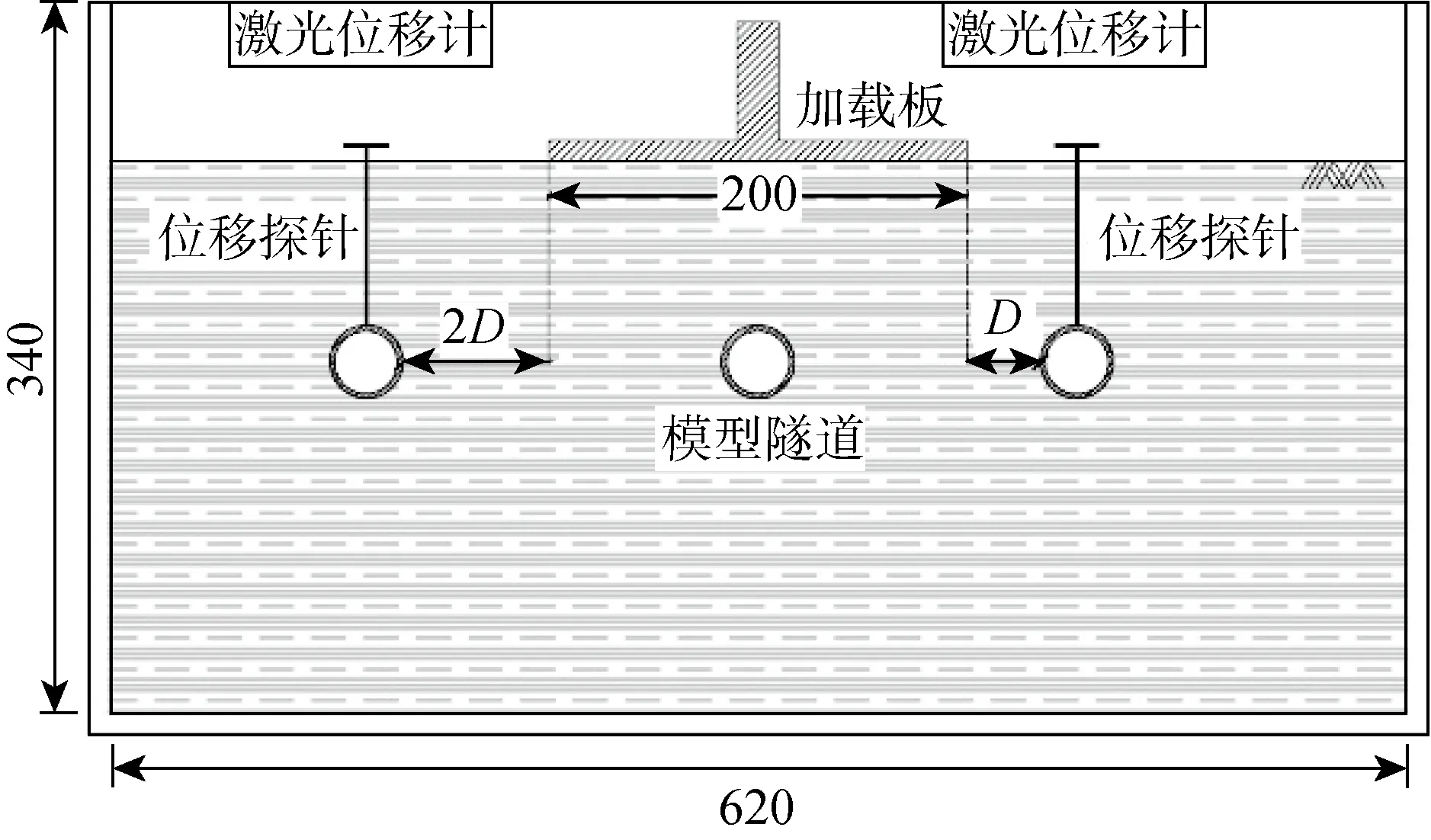
土体固结完成后，按照图3所示横断面示意图埋置模型隧道，隧道分别位于堆载正下方、侧方和2(为隧道直径)处.模型隧道直径为3 cm，壁厚为0.25 cm，埋深为10 cm.隧道由铝合金空心管加工而成，密度为 2 700 kg/m.在隧道顶部粘贴位移探针，通过高精度激光位移计实时记录隧道位移.图4所示为模型实物图.

这是器乐综合课中常用的方法，集各种器乐教学方法和训练手段于一身，运用多种乐器进行独奏和合奏的混合训练，在分分合合的演奏中培养学生的器乐配合能力，提高学生的音乐综合素质。

1.2 试验过程

本试验设计了宽度为20 cm的加载板，模拟实际20 m堆载宽度.试验通过离心机机械手对土体逐级施加荷载，从0开始每级增加5 kPa直至 50 kPa.每级加载完成后，通过高清摄像机拍摄模型整体变形情况.试验结束后，利用粒子图像测速(PIV)技术分析土体变形和隧道位移.

1.3 试验结果

..土体变形图5所示为通过PIV技术分析得到的离心模型试验土体变形矢量图，图中为地表宽度；为地层深度.可以看出，堆载下方土体受挤压向深部运动，位移矢量从地表逐渐向地层深部和两侧扩散.随着堆载的增大，受影响的土体范围越来越大，但主要集中在堆载正下方，影响区域外轮廓呈抛物线形.

..隧道位移图6所示为隧道位移与堆载的关系.将试验结果按发展趋势拟合后(图中虚线)可以发现，堆载正下方隧道受影响最大，位移增长呈抛物线形.两侧隧道受影响略小，位移发展近似呈线性.考虑到软黏土具有高压缩性和低承载力的特征，堆载周边土体发生局部剪切或刺入式破坏，隧道-曲线不会出现明显的拐点.

试验所用土体为上海第④层淤泥质重塑黏土，该层土为典型的结构性海相软土，归一化割线切变模量最小.为模拟实际场地应力，保证试验土体与原状土的物理力学性质基本一致，对重塑泥浆采用离心固结，在100离心力条件下旋转3～4 d，待固结度达90%，完成固结.

2 HSS模型适用性分析

为了确定适用于软黏土堆载问题的本构模型，参照离心试验建立数值计算模型，对比 HS模型和HSS模型计算结果，分析小应变土体硬化模型在地面堆载问题中的适用性.

2.1 数值模型建立

图11所示为两种本构模型地层应变等值线.HS模型隧道周围的土体应变范围为0.01%～0.02%，HSS模型隧道周围土体应变小于0.01%，两种本构模型下隧道周边土体应变均在小应变范围(0.001%～0.1%)内，土体刚度的发展对正确评估土体变形至关重要.

2.2 本构模型参数确定

2.3 计算结果对比

图9所示为两种本构模型下堆载增大至 50 kPa 时的地层总位移()云图，虚线处的地层深度等于1倍地表堆载宽度可以看出，未考虑土体小应变刚度的HS模型较HSS模型地层变形结果和影响范围都偏大，深度影响范围超过了1倍堆载宽度，水平影响范围达到了2倍堆载宽度；而HSS模型地层变形集中在堆载正下方，深度和水平影响范围均在1倍堆载宽度以内，与离心模型试验结果一致.

所调查医学生沟通能力总分处于14～84分之间，总分≥71分者即绩优组共246人，平均得分为（74.55±3.45）分；总分＜71分者即绩平组731人，平均得分为（57.73±10.19）分。不同性别的医学生沟通能力比较，差异无统计学意义（P＞0.05）；不同年级、专业、是否参加医患沟通课程医学生的沟通能力比较，差异均具有统计学意义（P＜0.05），见表1。

为研究对隧道位移的影响，以=8、=0位置隧道为例，隧道位移计算结果如图19所示可以看出，在同一级荷载下，随着隧道埋深的增大，隧道位移逐渐减小，隧道埋深与位移近似呈反比例函数关系：随着隧道埋深的增大，地面堆载产生的附加应力对隧道的影响越来越小，位移趋向于无穷小.

数值计算模型尺寸和隧道布置参考离心模型试验，计算简图和网格划分情况如图7所示.模型顶面为自由边界，其余边界受法向约束.计算模型初始地应力后，通过单元生死功能实现土体开挖和隧道施工，位移归零后，逐级施加地面堆载至50 kPa.

提取两种本构模型不同深度土体单元的剪切刚度计算结果，如图12所示.HSS模型=9 m处土体单元初始剪切刚度计算结果约为6 MPa，对照参考文献[16]，结果在合理区间内.HS模型的剪切刚度始终较小，处于HSS模型刚度衰减后的水平；而HSS模型土体单元具有较大的初始剪切刚度，且随着应变的增加，刚度呈S型曲线衰减，符合土体剪切刚度随应变发展的一般规律.

住宿环境升级，确保住得舒心。生活无烦恼，全县5个乡镇有室内独立卫浴的周转房占80%，其他房间均配备楼层卫生间、洗澡间、洗衣房。健身有去处，室内健身有跑步机、卧推架、单车等器材，户外锻炼有篮球、羽毛球、兵乓球等场地。减压有场所，减压室配置拳击手套、橡皮人等减压用具，文娱室配备象棋、围棋、纸牌等，小影院可满足20人观影需要。医疗有保障，在健康小屋配备温度计、血压计、体重秤，常备家庭药箱，备足日常药品。

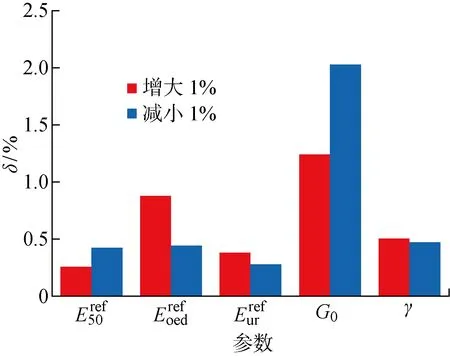
为了确定隧道位移对本构模型参数的敏感程度，利用上述有限元模型分析隧道位移对这些参数的敏感性，在保证其余参数不变的情况下仅改变一个参数分析其影响规律.计算各参数值增大或减小1%所引起的隧道位移改变的百分数，如图13所示.可以看出，隧道位移对初始切变模量敏感性最大，对其他参数敏感性相对较小.

对比土体变形、隧道位移和剪切刚度，可以发现针对上海软土地区隧道上方的地面堆载问题，考虑土体小应变刚度的本构模型能够更真实地反映地面堆载引起的土体变形和隧道位移特征.

2.4 HSS模型适用范围

基于HSS模型，任取某一宽度堆载建立无隧道时的数值模型，地层参数同表1，得到堆载下方地层应变随荷载的变化规律，如图14所示.可以看出，地面荷载较小时，堆载下卧地层均处于小应变范围(0.001%～0.1%)，此时土体主要发生弹性变形，如图14(a)所示.荷载增大后，堆载边缘部分土体发生应力集中，该部分土体应变首先增大，超出了小应变范围(大于0.1%)，如图14(b)所示.随着荷载进一步增大，角点部位土体应变继续发展，呈“泡型”向深部和两侧扩散，堆载下部土体应变也有所增加，如图14(c)所示.当荷载继续增大，堆载边缘部分土体应变迅速发展，出现塑性破坏，而此时堆载下方大部分土体仍处于小应变范围，如图14(d)所示.

相应于堆载下卧土体应力状态的3个阶段，有两个临界荷载，如图15所示，其中从压缩阶段过渡到剪切阶段的界限荷载为临塑荷载，从剪切阶段过渡到隆起阶段的界限荷载为极限荷载.由上述计算发现，HSS模型可以很好地反映地基土压缩阶段土体变形和隧道位移变化特征，而当荷载超过后，堆载边缘部分土体很快进入剪切阶段，应变超出小应变范围，计算不再适用.因此，HSS模型适用于地基土处于压缩阶段，即适用于地面荷载达到地基土临塑荷载前的隧道位移计算.

3 地层变形发展模式

为研究和对隧道位移的影响，令=0，将各工况按归一化后，发现隧道的-曲线具有相同的变化趋势以=12为例，隧道-曲线如图21所示，越大，隧道埋深相对越浅.可以看出，随着堆载荷载的增大，隧道位移呈抛物线形增长，且隧道埋深越浅，隧道位移增长越快.

4 地面堆载对隧道位移的影响

在土层特性确定的情况下，隧道位移取决于堆载规模和隧道位置，即堆载宽度、堆荷、隧道埋深和隧道圆心至堆载中心线的距离，如图17所示.为讨论各参数对隧道位移的影响，建立地表宽度为100 m，地层深度为50 m的数值计算模型，地层和隧道参数如表1和2所示.考虑了9种堆载宽度(=, 2, 3, 4, 6, 8, 9, 12, 16)、4种隧道埋深(=, 2, 3, 4)以及5种距离(=0,, 2, 3, 4)的情况，共计144组计算工况.

两种本构模型计算得到的隧道竖向位移与离心试验结果对比如图10所示.可以看出，两种本构模型计算的-曲线均为平滑曲线，没有明显的拐点.HSS模型计算结果与离心试验结果吻合较好，而HS模型由于忽略了土体小应变刚度，位移结果明显偏大，约为HSS模型的4～5倍.

4.1 单因素影响研究

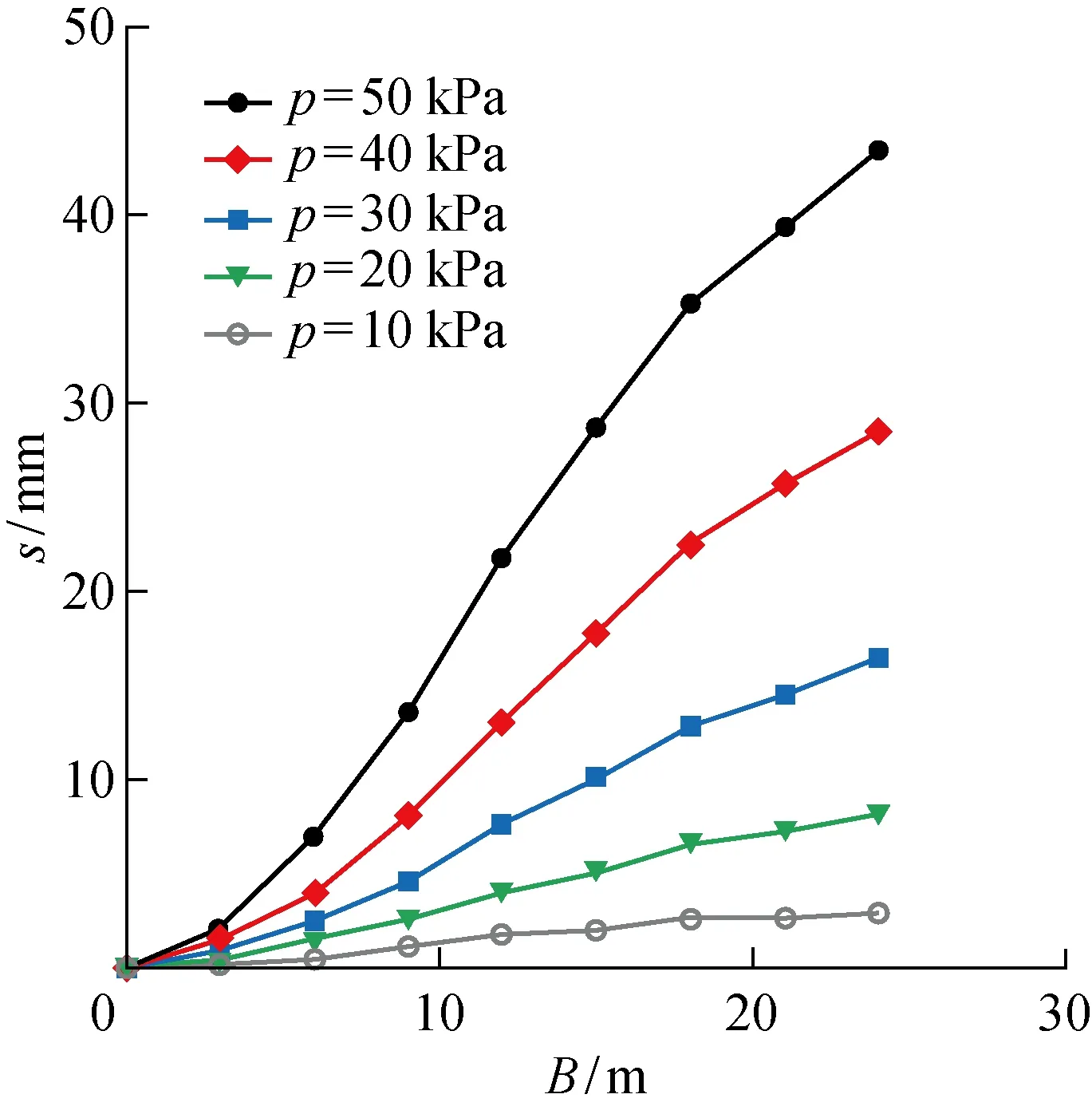
为研究堆载宽度对隧道位移的影响，以埋深=3、距离=0位置隧道为例，隧道位移计算结果如图18所示可以看出，在同一级荷载下，随着地面堆载宽度的增大，隧道位移不断增大，堆载宽度与位移呈非线性关系，当地面堆载宽度大于1倍隧道埋深后，隧道位移随堆载宽度增加而增大的速度减缓，有收敛趋势.

馆藏资源建设是图书馆服务实施开展的基石，是高校图书馆工作的重中之重[27]。馆藏资源从纸质向电子资源转型是图书馆发展的必然趋势，在大数据时代，用户如何获取信息，除了系统的传统的服务外，高校图书馆的数据素养教育实践表现形式主要为课程教育与在线教育，讲座、专题讨论会，专题培训[28]；以及个性化咨询就成为了图书馆服务转型的主要服务渠道。嵌入式服务对象以教师、研究人员和学生为主，如何让用户直接获得清晰、明确、有效的检索结果是服务的重点。

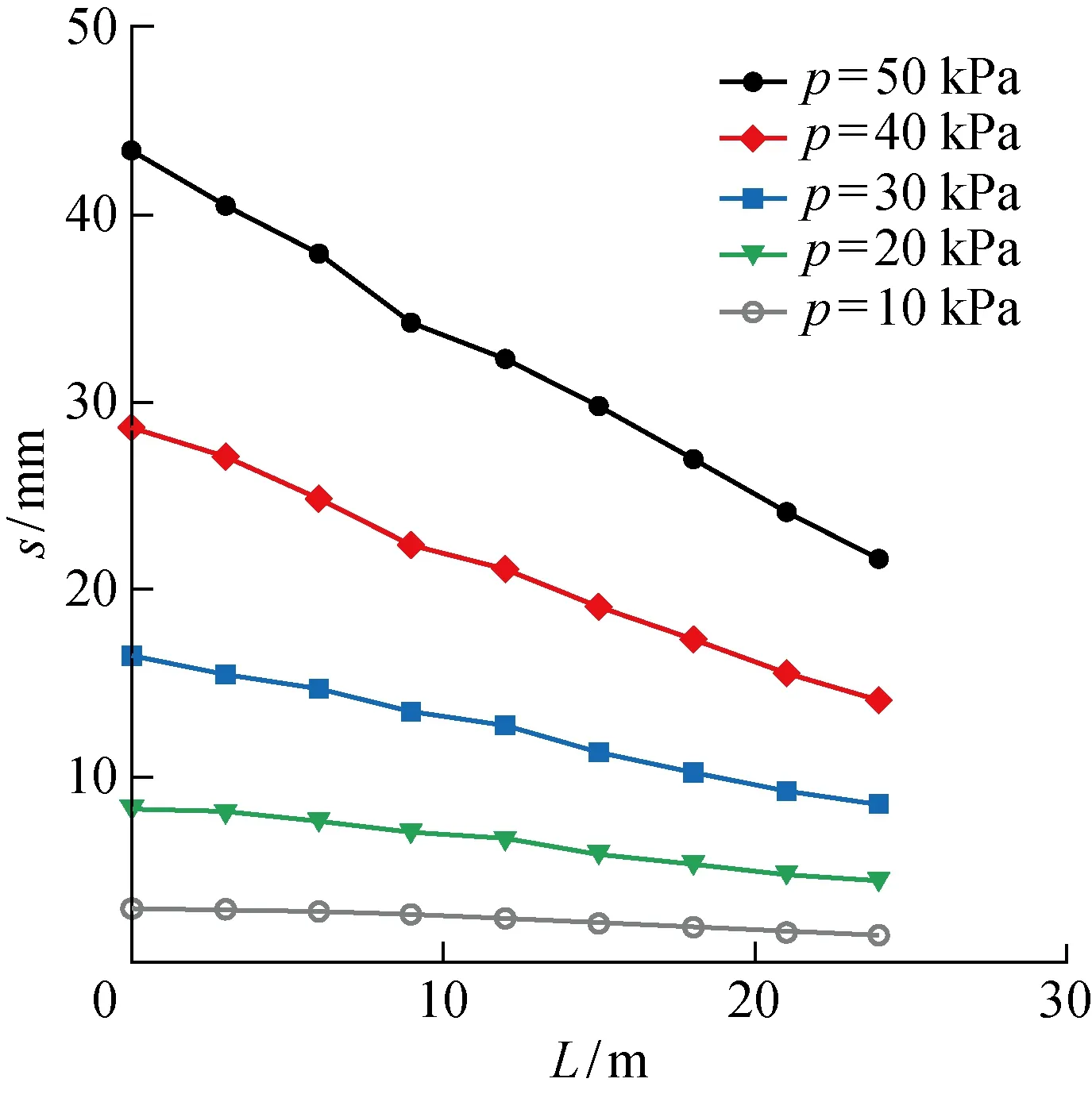
为研究距离对隧道位移的影响，以=8、=4位置隧道为例，隧道位移计算结果如图20所示可以看出，在同一级荷载下，随着距离的增大，隧道位移逐渐减小，与近似呈一次函数关系.

4.2 多因素影响研究

任取某一宽度地面堆载建立无隧道时的数值模型，分析下卧土体处于压缩阶段时，地层变形随荷载增大的变化发展规律，如图16所示，红线为地层变形等值线.当荷载非常小时，仅引起堆载中部区域土体发生很小的变形，如图16(a)所示.荷载增大后，堆载边缘土体应力迅速增大，使边缘部分土体影响扩大，地层变形等值线呈马鞍形，如图16(b)所示.随着堆载进一步增大，堆载正下方土体受挤压，地层变形等值线变为倒钟形或抛物线形，如图16(c)、16(d)所示.当荷载继续增大，堆载下方扰动范围向地层深部和两侧扩大，深度和水平影响范围逐渐超过了1倍堆载宽度，地层变形等值线变为椭圆形，如图16(e)、16(f)所示.当隧道位于地层变形某一影响区域内时，便可能产生相应的位移.

对两组患者不同护理干预后的满意度进行对比，实验组的满意度优于对照组，差异具有统计学意义（P＜0.05），详见表2。

中，教师要根据学生的元认知情况，精心设计问题，让学生通过“微型探究”活动，深化知识内涵，揭示数学本质，感悟解题方法.在具体问题解决后应注重引导学生总结提炼一般方法，使学生对问题的理解与思考达到新的高度.

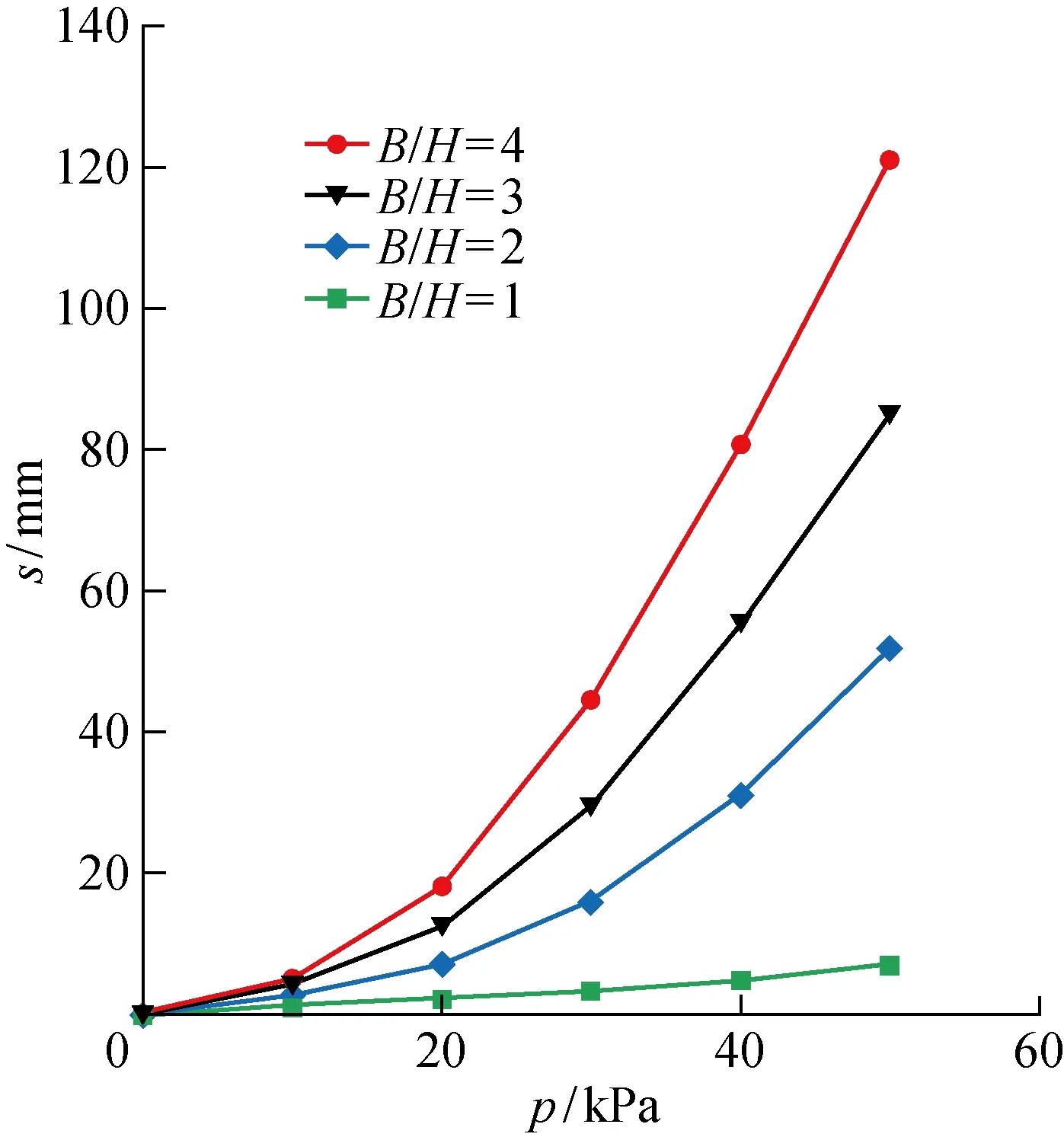
为研究和对的影响，将各工况按归一化后，发现在不同工况组合下，隧道位移均以竖向位移为主，水平位移较小，隧道的-曲线也具有相同的变化趋势.图22所示为=5、=3时隧道的-曲线，越大，隧道越靠近堆载中心线.可以看出，随着堆载荷载的增大，隧道位移呈抛物线形增长，且隧道与堆载中心线的距离越近，隧道位移增长越快.

(7)植被指数指标。利用遥感数据计算出研究区植被指数，并进行0～1之间归一化处理得到植被指数归一化结果(图3g)。

4.3 堆载规模与隧道位置综合影响研究

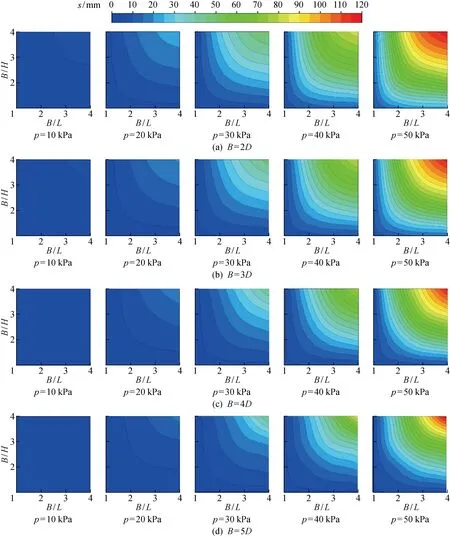
将按和归一化后，各工况隧道位移如图23所示.可以发现，当地面堆载较小时(小于 10 kPa)，不同堆载宽度和隧道位置组合下，隧道产生的位移都将在10 mm以内.堆载增大至20 kPa后，除了=2，其他几种情况一般不会产生大于20 mm的位移，这和隧道与堆载的绝对距离有关.随着荷载的增大，隧道在安全位移限值(20 mm)内的可能性越来越小.由于本模型中土体剪切刚度为上海浅层土中最小值，结果偏于保守，工程上可以综合考虑堆载规模和隧道位置，参考图21，将堆载控制在相应荷载级别下的安全位移限值内.

2018年8月30日，江苏南通一名13岁少年沉迷网游坠楼身亡。有关记录显示，十一点四十六分该少年还在玩游戏，十二点多钟跳楼，少年玩的是“吃鸡”游戏，里面有小孩跳楼情节。