基于图神经网络的联合用户调度与波束成形优化算法

何世文，袁军，安振宇，张敏，黄永明2,，张尧学

（1.中南大学计算机学院，湖南 长沙 410083；2.东南大学移动通信国家重点实验室，江苏 南京 210096；3.紫金山实验室，江苏 南京 211111；4.湖南邮电职业技术学院信息通信学院，湖南 长沙 410015；5.清华大学计算机科学与技术系，北京 100084）

0 引言

近年来，随着智能手机与新兴高清多媒体应用的普及，网络流量呈指数级增长。为了满足用户对这些新兴业务的服务质量需求，无线网络的部署呈现越来越密集化与小型化趋势。然而，网络密集化不仅会提高基础通信设施的建设成本，还将加剧小区间的同频信号干扰，使小区边缘用户面临相对较弱的小区内与较强的小区间的信号干扰问题。因此，无线密集网络亟须一种先进的干扰缓解技术来提高频谱效率与增强网络和速率[1]。近年来，协作多点（CoMP,coordinated multi-point）传输作为一种频谱效率优化技术，通过将多小区通信单元组成一个分布式协作集群系统以降低小区间的同频信号干扰，从而提高无线网络的覆盖率与小区边缘用户的服务质量[2]。

CoMP技术主要包含2种模式[3]，即联合发送（JT,joint transmission）和协同调度/波束成形（CS/CB,coordinated scheduling/beamforming）。2 种传输模式的主要区别在于，JT 模式下的用户可以由多个基站共同服务，而CS/CB 模式下同一用户只能接受一个基站的服务[4]。在现有的工作中，2 种传输模式均被广泛采用以提高网络的频谱效率[5]。例如，文献[6]利用 JT-CoMP 模式与非正交多址接入（NOMA,nonorthogonal multiple access）技术相结合的方式进行用户调度与功率分配优化。文献[7]研究了基于CS/CB-CoMP 模式的用户选择和迫零波束成形（ZFBF,zero-forcing beamforming）策略，以实现单小区调度增益与多小区干扰惩罚平衡。在CoMP 技术中，用户调度与波束成形是分别位于媒体访问接入层和物理层的2 个基本问题，其通常被单独研究，包括不考虑波束成形的用户调度问题[8]，以及基于固定用户集的波束成形问题[9]。

随着网络架构及硬件设备的发展，不同网络层级的跨层优化[10]有望进一步提高网络性能和资源利用率。研究者开始考虑用户调度与波束成形的跨层（媒体访问接入层和物理层）优化问题。例如，文献[11]提出了一种基于CS/CB-CoMP 模式的联合用户调度与波束成形策略，以支持超密集网络的海量设备互联场景服务。文献[12]利用正交随机波束成形技术，研究了基于JT-CoMP 模式的大规模多输入多输出（MIMO,multi-input multi-output）系统的联合波束激活和用户调度问题。文献[13]提出了基于迫零波束成形和用户调度（ZFBF-US,zero-forcing beamforming and user scheduling）的贪婪优化算法，以及基于连续凸近似理论的用户调度与波束成形（SCA-USBF,successive convex approximation based user scheduling and beamforming）的优化算法，但是两者均存在局限性，即前者计算效率过低，而后者性能不足。此外，这些基于凸优化理论（模型驱动）的优化算法不仅计算复杂度高，难以适应无线网络的低时延要求，而且当网络环境发生变化时，需要重新运行算法，未能有效利用网络历史数据信息。

随着人工智能技术，特别是图神经网络（GNN,graph neural network）在无线通信领域的发展应用[14]，越来越多的研究人员开始探索无线传输智能优化理论[15]。例如，针对设备到设备（D2D,device-to-device）网络中的无线资源优化问题，文献[16]尝试引入GNN来解决干扰信道中的用户功率分配问题，与经典的最小化加权均方误差（WMMSE,weighted minimum mean square error）功率分配算法相比，该模型更具性能和计算效率优势。文献[17]设计了一种基于图嵌入的D2D 网络链路调度算法，但是它并不适于衰落信道模型。为此，文献[18]提出了一种适于衰落信道的基于GNN的监督学习框架，并且在D2D 网络的链路调度问题和联合信道与功率分配问题中验证了算法的性能与泛化性优势。文献[19]研究了密集网络中的功率分配和波束成形2 个优化问题，并将固定的调度用户集的链路状态建模为图，进而将其转换为图优化问题。针对所考虑的图优化问题，文献[19]设计了一种适用于大规模用户场景的无线信道图卷积网络算法，该算法的性能表现能够匹配甚至优于传统优化算法。文献[20]研究了密集异构网络的联合用户调度与功率分配问题，并提出了一种基于GNN的半监督图表示学习算法，但是该问题没有考虑用户的服务质量（QoS,quality of service）需求。文献[21]针对具有不同类型设备的多小区多用户蜂窝网络的功率分配问题，设计了一种能够在异构图上进行学习的HetGNN（heterogeneous GNN）模型，其拥有比传统的深度神经网络更低的训练时间开销和计算复杂度。值得注意的是，在上述所讨论的有关GNN 模型的无线传输优化方案的研究中，均没有考虑用户调度与波束成形的联合优化问题，而是将它们作为2 个子问题进行单独讨论。

在考虑用户服务质量需求的条件下，通过结合上下行对偶理论和图神经网络，本文提出一种智能优化算法，用于解决多小区多用户JT-CoMP 网络的联合用户调度与波束成形问题。相比于传统优化算法[13]，所提算法不仅实现了更低的计算复杂度，还具有与其相匹配甚至更优的性能表现。本文主要的研究工作如下。

1) 建立多小区多用户JT-CoMP 网络的下行链路协作通信系统模型，旨在降低跨小区用户的同频信号干扰并提高频谱效率。具体地，在满足用户最小速率需求和基站最大发射功率约束的基础上，本文研究用户调度与波束成形的联合优化问题，并以网络和速率最大化为目标。该问题是一个非凸的混合整数连续变量组合优化问题，难以求解。

2) 利用上下行对偶理论与基础的数学转换，将原始优化问题转换为虚拟上行链路的联合用户调度与波束成形问题。为了利用图神经网络进行学习与优化，对多小区协作系统的用户链路状态进行图表示，将无线传输方案优化问题表示为一个图优化问题。针对该图优化问题，设计一种基于空间域GNN的M-JEEPON 模型用于用户调度与虚拟上行链路功率分配，并结合波束成形的解析公式，进而设计联合用户调度与波束成形的智能优化算法。

3) 为了验证所设计的M-JEEPON 模型的有效性，将其与传统优化算法进行性能比较。仿真分析表明，所提算法能够实现与传统算法相匹配甚至更优的性能表现。此外，通过对所提算法理论计算复杂度的分析，发现其在计算效率上也具有优势。

1 系统模型

考虑一个多小区多用户下行链路联合发送无线通信系统，其包括M个具有Nt根天线的基站（BS,base station）和K个待服务的单天线用户设备（UE,user equipment），如图1 所示。为了表示方便，令M={1,2,…,M}表示协作系统中的基站集合，K={1,2,…,K}与 S={1,2,…,K∗}⊆ K分别表示总用户集与调度用户集；令pk≥ 0表示协作系统中分配给用户k的下行链路传输功率，hk∈CMNt×1与w∈CMNt×1分别表示用户k的级联信道向量与单位波束向量，即基于以上表述，用户k的接收基带信号yk可表示为

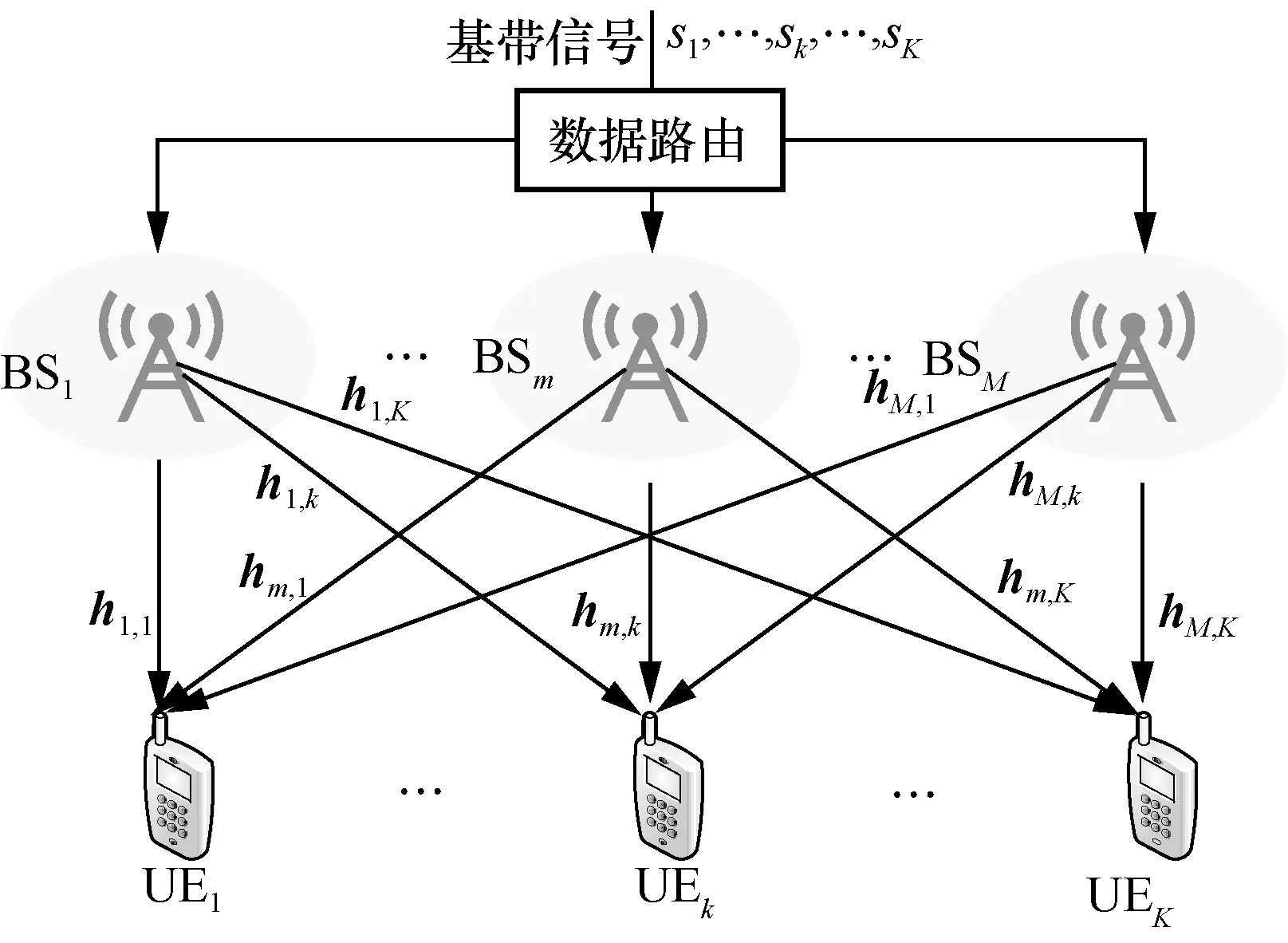
图1 多小区多用户下行链路联合发送无线通信系统

本文以最大化多小区协作系统的和速率为目标，研究联合用户调度与波束成形优化问题，同时考虑调度用户最小速率需求与基站最大发射功率约束。因此，该联合优化问题被建模为

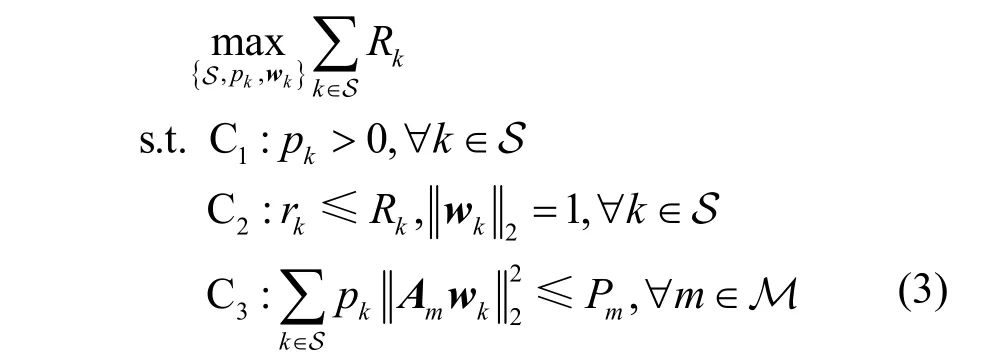
其中，Pm表示协作系统中基站m∈M的最大发射功率；Rk=lb(1 +γk)与rk>0分别表示用户k∈S的速率与最小速率需求；pk表示调度用户集S 中的用户下行链路功率且pk>0；Am表示协作系统中第m∈M 个基站的置换矩阵，定义为

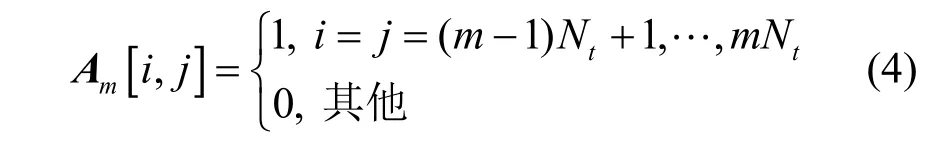
优化问题式(3)具有一个非凸的和速率最大化目标，其调度用户集S 是关于0-1 用户选择的整数变量优化，而用户速率约束和基站发射功率约束是关于功率向量和波束向量的连续变量优化。因此，优化问题式(3)是一个非凸的混合整数连续变量组合优化问题。优化问题式(3)的求解涉及多个子问题的联合优化，包括调度用户集S的选择、下行链路功率的分配，以及波束向量{wk}的设计。类似于文献[13]，优化问题→式(3)被改写为

引入二元指示向量κ，使原始优化问题的用户集范围从不确定的调度用户集S 转变为确定的总用户集K。进一步地，将优化问题式(5)的指示向量κ由离散值转换为连续值，得到优化问题式(7)，即

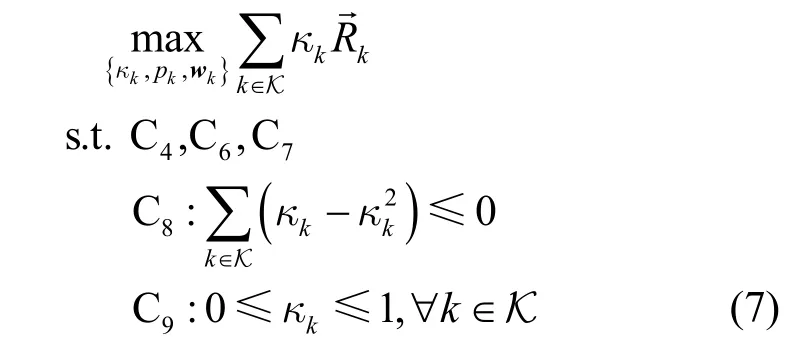
为了简化求解，将下行链路优化问题式(7)转换成虚拟上行链路对偶优化问题式(8)[13]，即

注意到，优化问题式(10)与优化问题式(7)的不同之处不仅是问题所考虑的传输链路不同，还包括波束向量W的求解方式不同。其中，在下行链路优化问题式(7)中，W需要迭代优化，而在优化问题式(10)中，W是通过关于虚拟上行链路功率的解析公式求解得到的，不需要迭代优化。考虑对偶问题式(8)的外层优化部分时，固定内层的优化向量{κ,q}和波束向量W，通过次梯度法更新对偶向量λ，即

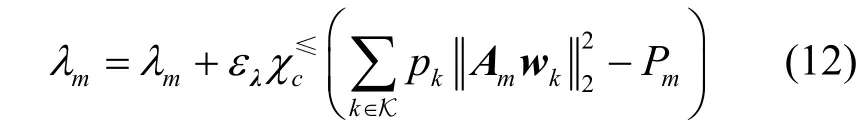
其中，p=[p1,p2,…,pK∗]T表示下行链路功率向量，1∈RK∗×1表示维度为K∗的全一向量，K∗表示调度用户集 S={ 1,2,…,K∗}中的用户索引最大值。矩阵Ψ定义为

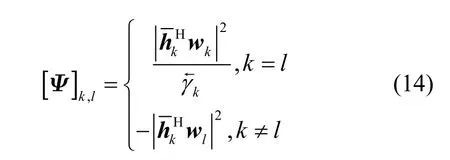
经过上述的数学推导和转换，相较于原始优化问题式(3)，对偶优化问题式(8)不仅解决了调度用户集S的不确定性问题，还将波束成形优化转变为虚拟上行链路功率分配优化。

2 联合用户调度与波束成形智能优化算法

前述工作通过上下行对偶理论与基础的数学转换，将原始下行链路优化问题式(3)转换为虚拟上行链路对偶优化问题式(8)，但是其内层优化部分式(10)仍然是非凸优化问题，难以直接求解。虽然文献[13]提出了用于求解该优化问题的基于ZFBF-US的贪婪优化算法，以及基于SCA-USBF的优化算法，但是2 种优化算法均存在局限性，即前者计算效率低，而后者性能不足。值得注意的是，以上2 种基于模型驱动的优化算法均没有充分利用用户历史信道状态信息的统计学特性，一旦无线网络环境发生变化，就需要重新运行算法。

为了充分利用用户历史信道状态信息，以及降低优化问题求解的计算开销，本文借助图神经网络理论设计了一种联合用户调度与功率分配网络（M-JEEPON,multi-cell joint user scheduling and power allocation network）模型，并结合波束向量W的解析式，进而提出一种联合用户调度与波束成形的智能优化算法，具体实现过程如算法1 所示。其中，D={hk|k∈K} 表示协作系统中总用户集K的信道状态信息，Θ表示M-JEEPON 模型的网络参数集，Φ(D,Θ)={κ,q}表示M-JEEPON 模型输出的关于样本D的用户调度指示向量κ和虚拟上行链路功率向量q，而波束向量W通过解析式计算得到。接下来，本文将介绍算法1的步骤2)中有关M-JEEPON 模型的架构及训练算法。

算法1联合用户调度与波束成形智能优化算法

2) 将用户信道样本数据D 输入训练后的M-JEEPON 模型，输出关于样本D的联合用户调度和虚拟上行链路功率分配策略Φ(D,Θ)={κ,q}，并通过式(11)计算得到用户的波束向量W；

3) 通过虚拟上行链路功率向量q、用户波束向量W和式(13)计算得到下行链路功率向量p，求解下行链路的网络和速率值。

2.1 拉格朗日对偶问题

对偶优化问题式(8)的内层优化问题式(10)是一个具有多约束的组合优化问题。为了将优化问题式(10)转变为一个无约束的优化问题，本文将其约束项分为可投影约束集和不可投影约束集 C2={C8,C11}。其中，对于可投影约束集 C1，后续将采用合适的投影公式使其满足约束条件；对于不可投影约束集 C2，通过引入非负的拉格朗日乘子将C2中的约束作为惩罚项加入目标函数。具体地，引入非负的拉格朗日乘子{μ,ν∈ R+}（对偶变量），内层优化问题式(10)的部分拉格朗日松弛函数表示为

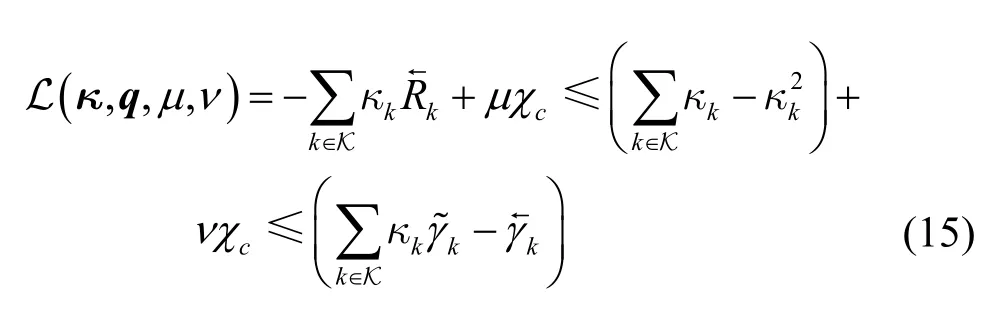
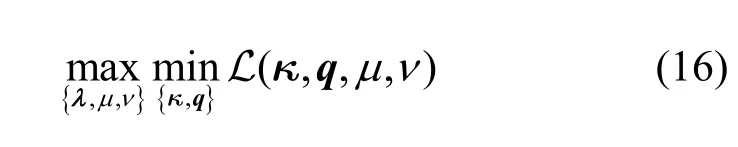
相应地，对偶变量{μ,ν}的更新方式为

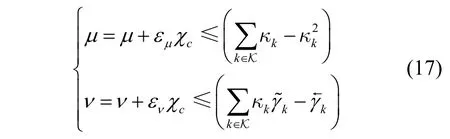
其中，εμ,εν∈R+分别表示对偶变量μ,ν的更新步长。为了方便表示，令Ω表示优化问题式(8)中可投影约束的可行域，其定义为

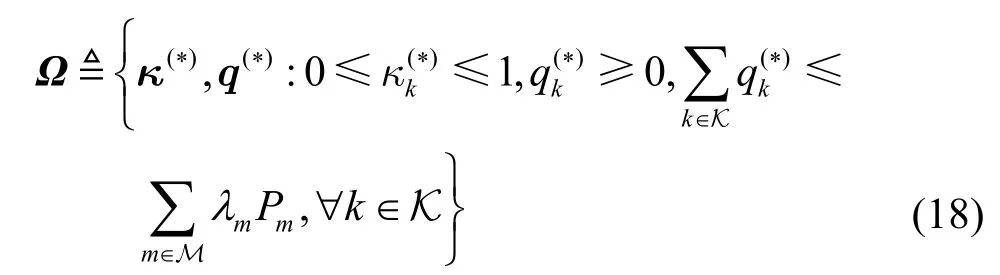
其中，{κ(∗),q(∗)}表示经过投影后的优化向量，且投影公式定义为

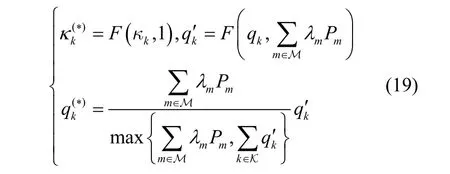
其中，F(z,t)=max{min{z,0},t},t>0为区间[ 0,t]的投影函数。基于以上的约束转换，对偶优化问题式(16)已经成为一个无约束优化问题。考虑内层子优化问题时，固定对偶变量{λ,μ,ν}，不断更新原始向量{κ,q}和波束向量W，以使松弛函数L 最小；当考虑外层子优化问题时，固定{κ,q}和W，并以次梯度方式更新{λ,μ,ν}。

不同于传统优化算法通过多次迭代的方式更新优化变量以寻求目标函数最优化，M-JEEPON 模型通过学习用户历史信道及网络拓扑数据与目标函数的映射关系，不断优化网络参数集以最优化目标值。在后续部分，将介绍无线网络图表示和M-JEEPON 模型。

2.2 多小区联合发送网络的图表示

本节通过设计一个无线网络图表示模块以结合用户历史信道状态信息和网络拓扑信息，并将组合优化问题转换为图优化问题。为了减少无线网络用户信道构图的复杂度，本节在构图过程中考虑将多小区联合发送网络中的多条用户通信链路与干扰链路进行合并，即系统内每个用户只有一条通信链路与多条干扰链路。为了描述方便，将无线网络的用户信道图表示为 G (V,E)，其中V 表示图的节点集合，E 表示图的边集合，且节点表示用户设备与联合基站的通信链路，而边则表示用户设备间的干扰链路。

图G (V,E)中的节点v∈V和边 Eu,v∈E 分别具有特征信息，定义为其中u∈V 为节点v的一阶邻居节点。如图2 所示，多小区联合发送网络被转换为一个虚拟的多用户干扰信道完全有向图。G (V,E)中的节点特征和边特征分别反映当前用户的通信链路特征与干扰链路特征。此外，通过构图方式可以发现，G (V,E)的规模与协作系统内的用户数K相关，图表示过程的计算复杂度为 O (K2MNt)，其中 O (⋅)表示通过Big-O 表示法统计的理论计算复杂度。

2.3 多小区联合用户调度与功率分配模型

前述工作将优化问题式(8)转换成无约束的拉格朗日对偶优化问题式(16)。在对偶优化问题式(16)的内层优化子问题中，传统优化算法通过多次迭代更新{κ,q}直至问题收敛，进而通过式(11)计算W。本节通过设计M-JEEPON 模型替代传统优化算法的迭代求解过程。在训练过程中，M-JEEPON 模型不断更新网络参数集来调整输出的{κ,q}，以使内层优化子问题的目标函数最小。

M-JEEPON 模型本质上可以看作输入的用户信道及网络拓扑数据与输出的{κ,q}及W的映射函数。作为一种空间域类型的图卷积网络，M-JEEPON模型被设计用于图上进行学习与优化，其具有多个图卷积层，各图卷积层之间采用基于消息传递机制的方式进行节点的消息聚合与嵌入表示向量更新[24]。具体地，节点v在M-JEEPON 模型的第ℓ 个图卷积层的优化向量更新规则定义为

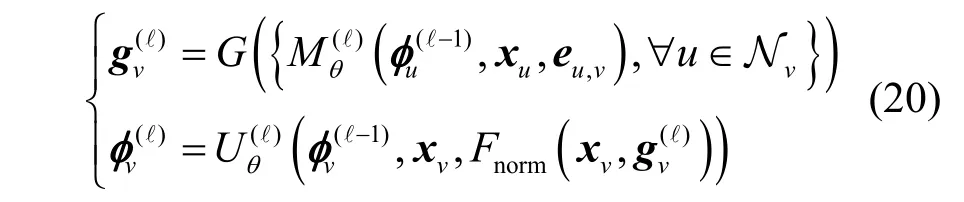
其中，Nv表示节点v的一阶邻域节点集；表示节点v在图卷积层ℓ的优化向量，且被初始化为全零向量，当图卷积层ℓ的消息传递过程完成后，节点v的嵌入表示向量更新为表示聚合消息标准化函数，即

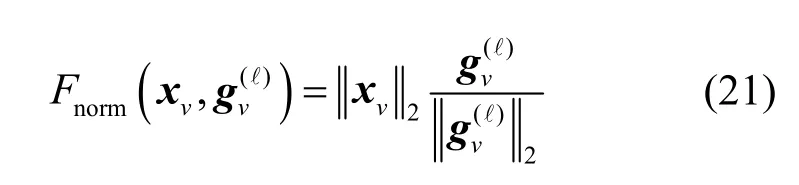
通过对节点聚合消息进行标准化处理，能够减轻由样本数据差异带来的影响，使M-JEEPON 模型在训练过程中保持稳定的学习分别表示节点消息生成函数与状态更新函数，通过具有不同结构的深度神经网络模块实现。G(⋅)表示消息聚合函数，用于汇聚属于各个节点与边的特征消息，其通过集合函数实现，如max(⋅)与mean(⋅)函数等。图3展示了智能优化算法架构（M-JEEPON 模型架构和波束向量求解层）和训练框架。M-JEEPON 模型架构包含图表示层、L个图卷积层与约束投影层，以捕获图中节点v的邻域节点与边特征信息。注意到，M-JEEPON 模型以用户信道数据输入D={hk|k∈K}，输出无线用户调度和虚拟上行链路用户功率分配策略Φ(D,Θ)={κk,qk}及波束向量W。

M-JEEPON 模型的训练过程反映的是无约束拉格朗日对偶问题式(16)的求解过程，其通过内层优化和外层优化交替迭代的方式不断更新M-JEEPON 模型的网络参数集Θ，直至训练阶段结束。M-JEEPON 模型的训练过程如算法2 所示，其包括两层循环步骤，分别为训练循环和样本遍历循环。算法2 中的步骤2)表示M-JEEPON 模型的图表示层，其在循环外部生成用户信道图表示，避免重复计算；步骤 5)和步骤 6)分别表示M-JEEPON 模型的图卷积层和波束向量求解层。一旦M-JEEPON 模型完成训练，就能够直接应用于算法1的步骤2)。

算法2 M-JEEPON 模型的训练过程

1) 初始化M-JEEPON 模型的网络参数集Θ、图卷积层数L，以及训练的次数

8) 循环结束；

9) 外层优化部分，通过式(12)、式(17)和记录的约束违背度，更新{λ,μ,ν}；

10) 循环结束；

11) 保存训练完成后的M-JEEPON 模型。

3 仿真分析

本节通过仿真实验比较 ZFBF-US 算法、SCA-USBF 算法和M-JEEPON 模型的性能表现，并在小规模系统场景验证3 种算法和用户调度与波束成形的穷举搜索（BFS-USBF,brute force search for user scheduling and beamforming）算法的性能差距。为了确保比较的公平性，传统优化算法收敛精度保持相同，并且以测试样本的平均和速率为比较目标，以平均调度用户数为参考目标，算法的结果分别表示为R1与R2。对于M-JEEPON 模型，其训练样本与测试样本也在相同的系统参数中被独立生成。此外，各算法的理论计算复杂度也将被讨论，以衡量算法的综合性能表现。

3.1 多小区信道模型与系统参数

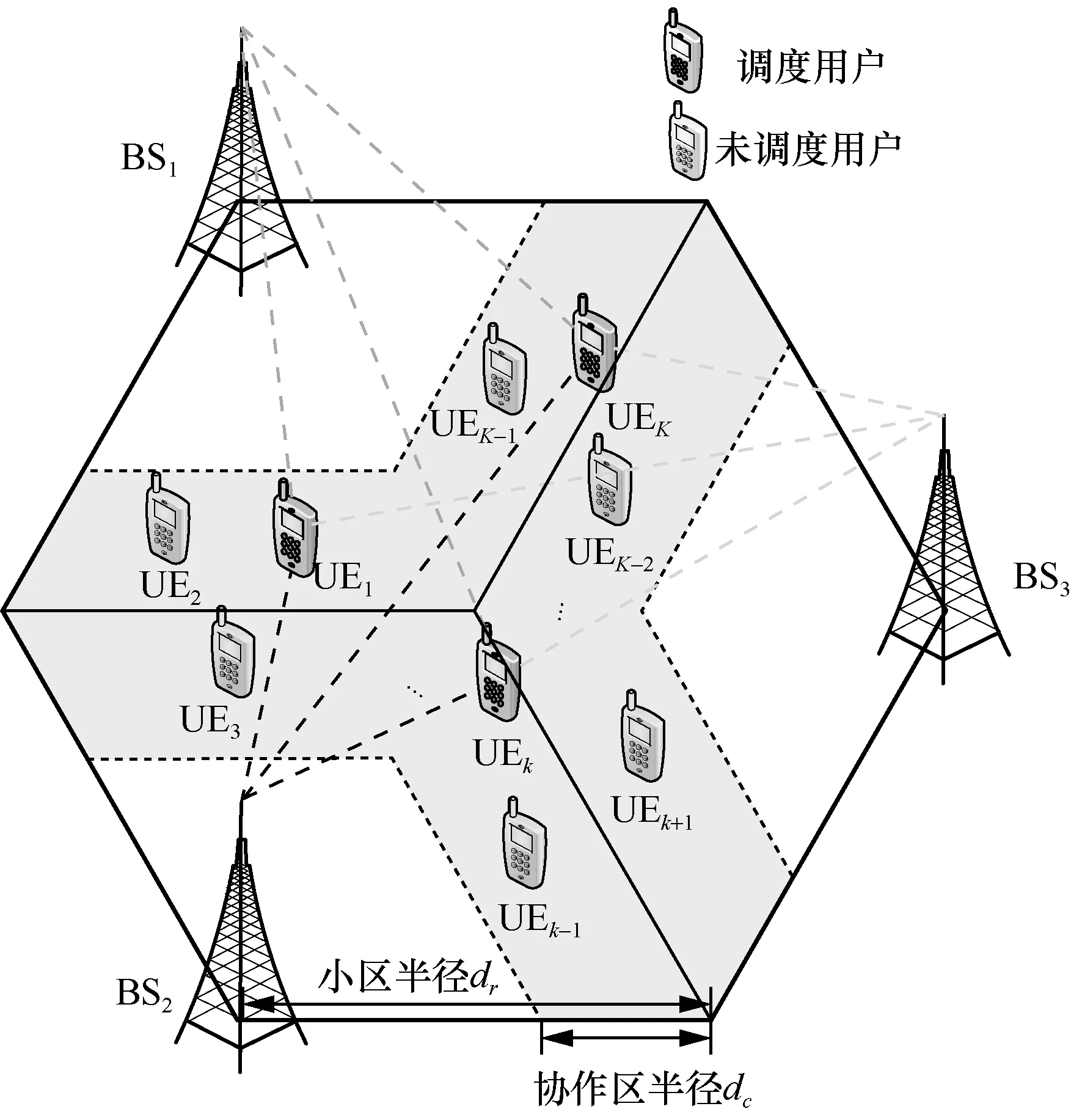
图4 多小区协作系统的用户分布

在实验中，M-JEEPON 模型的设计与实现基于 Pytorch 深度学习库，并采用学习率为η= 1 × 10−5的Adam 优化器[26]进行网络参数的更新。在训练过程中，设置训练迭代次数为200，而对偶变量{λ,μ,ν}的更新 步长为ελ,εμ,εν=1 ×1 0−5。为了评估M-JEEPON 模型与其他算法的性能，设置测试样本大小为500，训练样本大小为2 000，训练样本与测试样本相互独立且样本比例为4:1。此外，如无特殊说明，多小区协作系统的默认仿真参数如表1 所示。

表1 多小区协作系统的默认仿真参数

3.2 M-JEEPON 模型训练阶段的收敛性分析

本节探讨M-JEEPON 模型在训练阶段的目标函数和约束违背度的收敛情况。具体地，实验采用默认的系统参数进行仿真，测试M-JEEPON模型在训练阶段的目标函数曲线，以及不可投影约束集 C2={C8,C11}的约束违背度曲线，结果如图5 所示。从图5 可知，随着迭代次数的增加，M-JEEPON 模型的网络参数集被不断更新，致使模型输出的优化变量所对应的目标函数（和速率）值增大，并逐渐趋于稳定状态，这表明算法2的有效性。此外，随着迭代次数的增加，M-JEEPON 模型逐渐向约束违背度减小的方向发展，约束C8和约束 C11的违背度均逐渐趋于0。需要指出的是，M-JEEPON 模型并不能总是使输出的优化变量满足约束集 C2。一旦出现此情况，解决方案是先将用户调度向量κ稀疏化为0 或1，再根据优化向量{κ,q}和波束向量W剔除不满足用户最小速率约束的用户，最后输出满足约束集 C2的和W，并计算目标函数值。基于上述分析，M-JEEPON 模型在训练过程中能够使目标函数收敛，但是无法使输出的优化向量总满足约束集 C2，仍需要进一步处理，以使其满足约束条件。

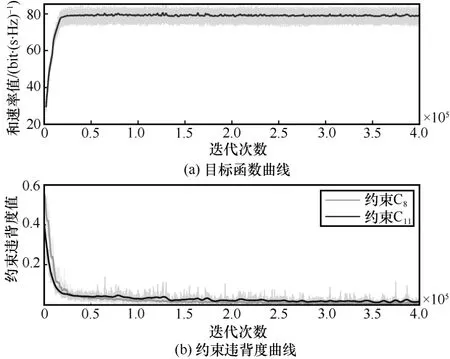
图5 训练阶段的目标函数和约束违背度曲线

3.3 不同用户数场景的算法比较

本节探讨协作系统中不同用户数K对算法性能的影响。具体地，采用2 种实验场景进行比较：1) 小规模场景，验证 ZFBF-US 算法、SCA-USBF 算法、M-JEEPON 模型与BFS-USBF算法的性能差距；2) 大规模场景，测试前3 种算法的性能表现。在小规模用户场景下，设置基站信噪比SNR=0，基站天线数Nt=2，用户最小速率需求rmin=1bit/(s·Hz) 与用户 数K∈ {4,6,8,10}；在大规模场景下，按照用户数K∈ {5,10,20,30}与 系统 其他默 认参 数进行实 验仿真。其中，小规模场景下不同用户数的算法结果如表2 所示。对比BFS-USBF 算法，M-JEEPON模型与SCA-USBF 算法都能够实现与其相接近的性能表现（R1值超过BFS-USBF 算法的92%），而ZFBF-US 算法则与其有着显著的差距。对比SCA-USBF 算法，虽然M-JEEPON 模型的R1值相对较低（R1值高于SCA-USBF 算法的93%），但是随着K的增加，M-JEEPON 模型的性能逐渐接近SCA-USBF 算法。此外，表2的结果也表明由K值增加所带来的多用户分集增益会使算法的R1值与R2值均得到提升。

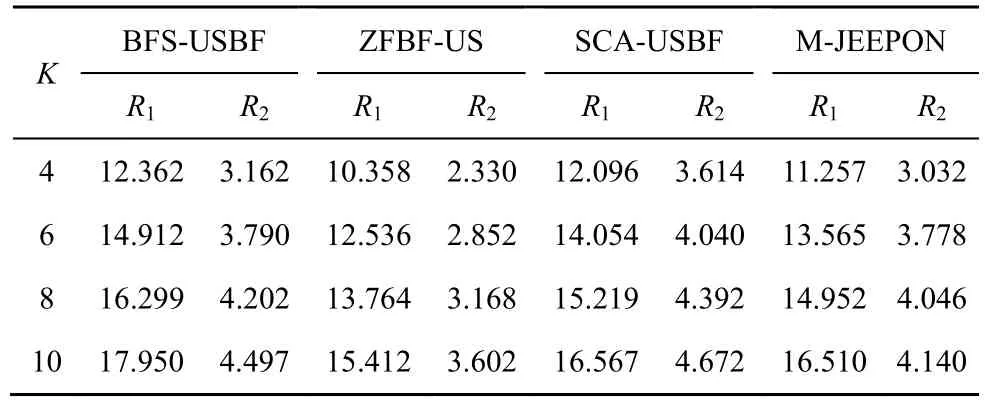
表2 小规模场景下不同用户数的算法结果

在大规模场景下，由于BFS-USBF 算法的计算复杂度过高，故不参与比较，其他3 种算法的结果如表3 所示。从表3 中可以发现，随着K的增加，M-JEEPON 模型的R1值逐渐接近并超过SCA-USBF 算法的结果，并且始终优于ZFBF-US算法。特别是，当K≥ 20时，ZFBF-US 算法的性能趋于稳定，但是它的R1值显著低于其他2 种算法的结果。这是因为SCA-USBF 算法与M-JEEPON模型是针对当前优化问题专门设计的，而ZFBF-US算法则是利用迫零波束成形与半正交用户选择以实现网络和速率最大化，无法保证结果最优。此外，表3 中的算法结果还反映了另一个现象，即当K≥ 10时，相较于另外2 种算法，M-JEEPON 模型虽然系统平均和速率更高，但是它所对应的平均调度用户数却并不是最多的。基于上述比较，在大规模场景下，M-JEEPON 模型更具性能优势。

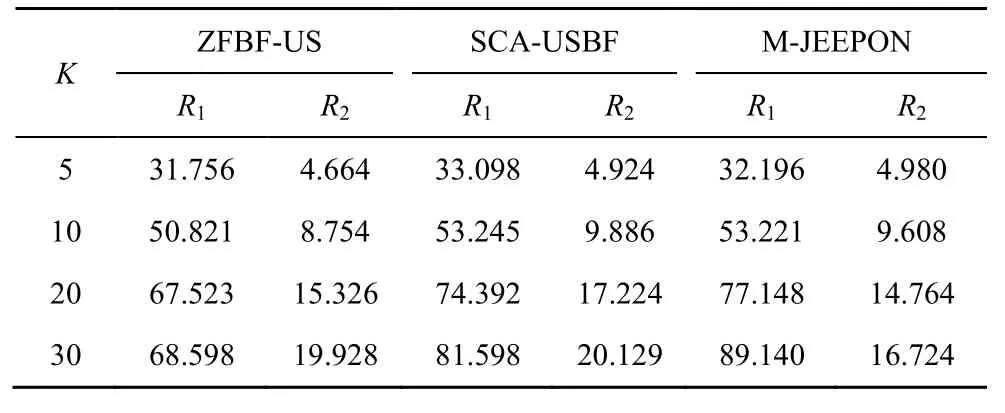
表3 大规模场景下不同用户数的算法结果

3.4 不同天线数场景的算法比较

本节探讨基站不同天线数Nt对算法性能的影响。为了避免用户规模可能对算法造成的影响，采用2 种K值的实验场景进行比较。具体地，实验设置基站天线数Nt∈ {4,6,8,10,12}与用户数K∈{ 10,20}，而其他参数采用默认值，结果如图6 所示。

从图6 可知，当K相同时，增大Nt值能够带来显著的多天线增益，使算法的R1值得到提升。当K=10时，M-JEEPON 模型能够保持与SCA-USBF算法相近的性能表现，并且此时系统内的绝大部分用户可以被调度。当K=20时，系统的资源无法支持调度所有用户，M-JEEPON 模型的R1值随着Nt值的增大逐渐接近并超过SCA-USBF 算法的结果，并且其性能一直优于ZFBF-US 算法。通过实验结果也可以观察到，ZFBF-US 算法在Nt=4场景下的R1值接近另外2 种算法的结果。这是因为基站天线数越少，ZFBF-US 算法越容易找到一组信道近似正交的用户组合，使其获得与另外2 种算法相近的性能表现。当Nt相同时，通过增大K值能够给3 种算法带来显著的性能增益，尤其是对于Nt=12的算法结果。这是因为当系统资源有限时，适当增加K值的大小，能够提高调度用户集的可选择性，有利于实现高的网络和速率。基于上述比较，通过增加基站天线数能够提高网络和速率，并且M-JEEPON模型相对另外2 种算法更能利用好多天线增益。

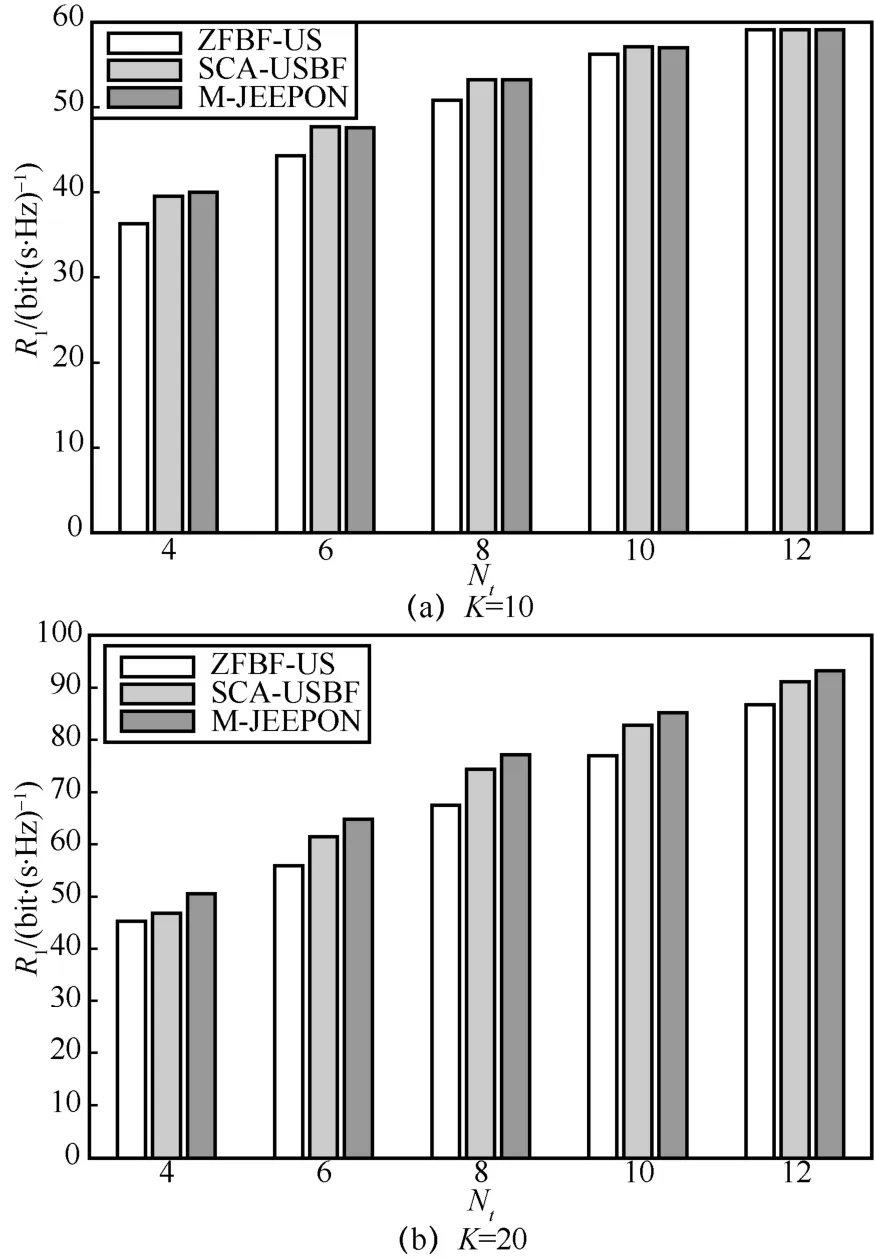
图6 基站不同天线数场景的算法R1值结果

3.5 不同信噪比场景的算法比较

本节探讨协作系统中基站不同信噪比对算法性能的影响。具体地，设置基站SNR∈{0,5,10,15,20,25}dB，而其他系统参数保持默认设置，算法R1值结果如图7 所示。从图7 可知，M-JEEPON 模型的R1值始终高于另外2 种算法，并且能够与SCA-USBF 算法保持一个稳定的状态。对比ZFBF-US 算法，当SNR 低于10 dB 时，M-JEEPON 模型更具性能优势；当SNR 超过10 dB时，ZFBF-US 算法与M-JEEPON 模型的R1值差距减小，但仍不高于后者R1值的94%。对比ZFBF-US算法与SCA-USBF 算法可以发现，随着SNR的增加，前者逐渐接近后者的R1值，但始终未曾超过后者。这表明，即使系统资源增加使优化问题的解空间增大，但是ZFBF-US 算法获得的依然是优化问题的局部解，而SCA-USBF 算法的解是近优解。

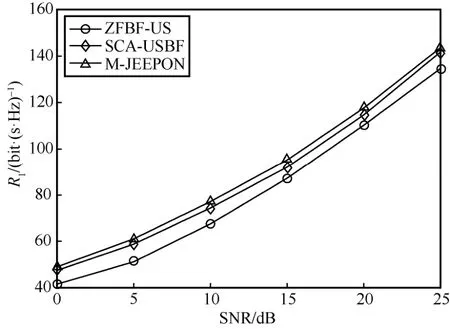
图7 基站不同信噪比场景的算法R1值结果

3.6 不同用户速率场景的算法比较

本节探讨协作系统中用户最小速率需求对算法性能的影响。具体来说，设置不同的用户最小速率需求而其他系统参数均保持默认设置，算法结果如表4 所示。从表4 可以看到，M-JEEPON 模型的R1值可以在不同的rmin值设置中取得更优的性能表现，并且SCA-USBF 算法的R1值也同样优于ZFBF-US 算法。

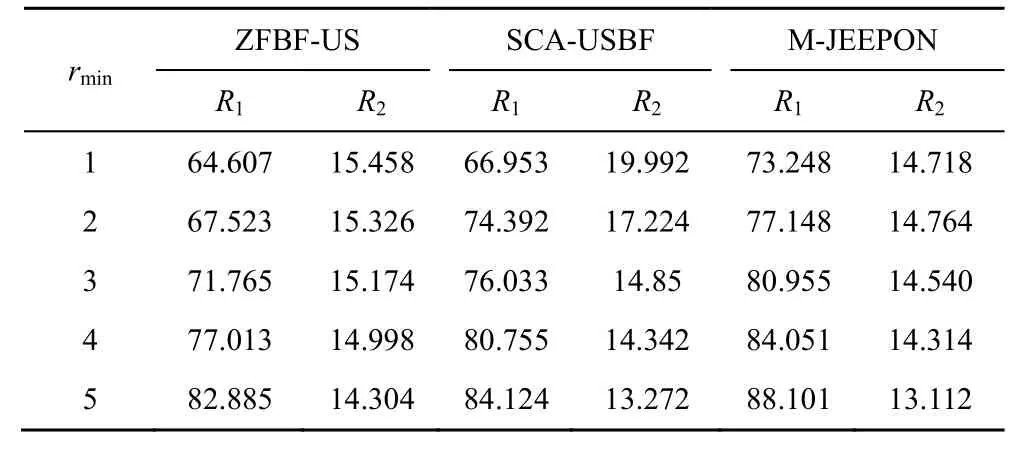
表4 用户不同最小速率需求场景的算法结果

此外，表4的结果也表明，当协作系统的总功率固定时，通过增大rmin能够提高3 种算法的R1值，但是相应的R2值将降低。这是因为rmin值的增加会导致协作系统能够调度的用户数减少，这间接减小了用户间的干扰，有利于算法获得更高的R1值。但是这并不意味着rmin值的无限增大会一直带来正向效果。可以预测的是，这最终会导致协作系统因为无法满足用户最小速率需求而无法调度任何一个用户，使算法获得的R1值为0。基于上述比较，M-JEEPON 模型在不同用户最小速率需求场景中能够取得更优的系统平均和速率表现。

3.7 不同算法的计算复杂度比较

为了直观地比较，本节讨论不同用户数K场景下各算法计算复杂度数量级，而其他系统参数保持默认设置，结果如图 8 所示。其中，BFS-USBF 算法的计算复杂度受K的影响极大，ZFBF-US 算法和SCA-USBF 算法次之，而M-JEEPON 模型最小。这是因为BFS-USBF 算法需要遍历所有可行用户组合，SCA-USBF 算法和BFS-USBF 算法的主要计算开销是波束优化部分，而M-JEEPON 模型的主要计算开销是神经网络模块，但其受K的影响并不明显，且波束向量通过解析公式求解，故其计算复杂度最低。基于以上分析，M-JEEPON 模型在算法计算效率方面也具有优势。

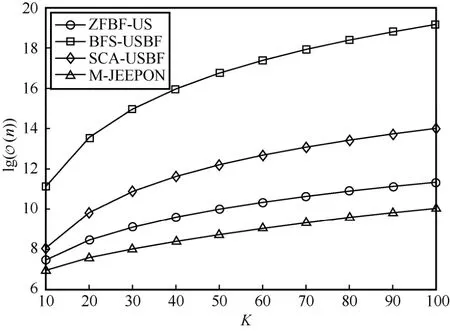
图8 各算法计算复杂度数量级

4 结束语

本文在考虑用户最小速率需求和基站最大发射功率的约束条件下，研究了多小区协作系统的联合用户调度与波束成形优化问题。为了降低传统优化算法的计算复杂度，本文将无线网络资源优化问题转换为图优化问题，进而设计了一种基于空间域GNN的M-JEEPON 模型，并结合波束向量解析公式提出了一种联合用户调度和波束成形智能优化算法。仿真分析表明，所提算法不仅在大规模系统场景具有更优的性能表现，同时也拥有比SCA-USBF 算法和ZFBF-US 算法更低的计算复杂度。在后续的研究中，将进一步探讨其他无线网络资源优化问题的智能化解决方案，以达到提高网络频谱效率和用户服务质量的目的。