参与无源网络虚拟调频的VSC-MTDC策略研究

2022-08-04罗兰王渝红宋瑞华毕经天陈诗昱万良彬

电气传动 2022年15期

罗兰，王渝红，宋瑞华，毕经天，陈诗昱，万良彬

（1.四川大学电气工程学院，四川成都 610065；2.中国电力科学研究院有限公司，北京 100192）

电压源型换流器高压直流（voltage source converter-high voltage direct current，VSC-HVDC）输电技术具有不存在换相失败、有功无功解耦可以单独对其进行控制、不需要换流站提供换相电压、设备占地面积小等优点[1-2]。柔性直流输电可以实现自换相，可工作在无源逆变的状态，因此可实现柔性直流输电系统向无源网络供电[3]。但柔性直流的内外环控制不能响应无源网络的频率变化，无法为无源网络提供频率支撑。虚拟同步发电机（virtual synchronous generator，VSG）技术[4-5]能为系统提供阻尼和惯性支撑，目前该技术在微电网逆变器以及分布式并网发电等领域研究相对较多[6]。VSG 控制策略具有一次调频和调压能力以及为无源网络提供惯性支撑能力[7]。

文献[8]推导VSG 小信号模型，给出了有功环和无功环解耦控制条件，给出了转动惯量和阻尼系数整定方法。文献[9]探讨了转动惯量和阻尼系数根据电网的实时运行状态，为了抑制频率偏离额定频率的变化，其参数可以进行自适应调整。文献[10]以直流电压相互协调控制为目标改进VSG 控制策略，提高了直流系统运行的稳定性。以上控制策略主要是对VSG 进行一次调频，系统频率不能回到额定值。文献[11]通过替换阻尼环节采用频率的PI反馈环节，解决孤网模式下频率偏移问题，实现无差调节。文献[12]将交流网络频率与直流电压相互的耦合关系考虑到U2—P的下垂裕度控制策略中，可以实现直流电网的功率平衡，该策略实现了电压源型换流器的多端直流（voltage source converter multi-terminal DC，VSCMTDC）输电系统的一次调频响应，属于有差调节。文献[13]在逆变站引入下垂裕度控制，其输出的差值作为VSG 有功控制环节的输入机械转矩，当直流电网中定电压控制站超出设定的电压裕度，该VSG控制的换流站具有后备定电压能力。

本文根据VSC-MTDC 换流站的电压下垂控制策略，提出一种虚拟调频器（virtual frequency regulator，VFR）控制策略，在传统虚拟同步发电机（traditional virtual synchronous generator，TVSG）控制基础上，利用PI控制器可以实现频率跟踪调节，将角速度差值进行PI 调节，消除角速度差值实现无差调频；其次引入直流电压的偏差，让换流站参与直流电压的调整，并对该控制系统稳定性进行分析得到合理的参数，最后对所提控制策略进行验证。

1 VSC-MTDC 系统描述及TVSG 控制原理

1.1 四端VSC-MTDC系统描述

四端的VSC-MTDC 系统如图1 所示，换流站1、换流站3 连接大电网，采用功率—电压下垂控制[14]；换流站2 经换流变压器与新能源并网连接，作为新能源送出，采用定功率控制；换流站4连接无源网络，采用虚拟同步发电机控制策略。

图1 四端VSC-MTDC系统Fig.1 Four terminal VSC-MTDC system

1.2 TVSG控制原理

TVSG 有功环节控制一般采用同步发电机的二阶模型进行模拟[15]，其表达式如下：

向无源网络供电的TVSG 有功—频率控制原理图如图2所示。

图2 TVSG有功—频率控制原理图Fig.2 Schematic of TVSG with active power-frequency control

无功控制环节主要依据逆变站输出无功功率偏差以及输出电压的偏差，经过PI控制环节得到调制电压幅值参考值Em，如下式所示：

无功环节控制器如图3所示。

图3 无功—电压控制原理图Fig.3 Schematic of reactive power voltage control

有功环节控制器输出相位θ作为调制波相位，无功环节输出参考电压Em作为调制波的幅值，可得脉冲宽度调制输入的三相调制波为

2 基于频率和直流电压偏差的VFR控制

无源网络中，频率差值为

式中：K为无源网络调频系数；ΔPL为无源网络负荷变化量；ΔPe为逆变站输出的功率改变量。

根据式（1）可知，TVSG 频率调节主要是通过改变功率进行调节，当系统进入稳态时，其关系如下式所示：

式中：K0为TVSG一次调频系数。

式（5）为TVSG 控制模拟系统的一次频率调节，属于有差调节。

当无源网络负荷变化时，无源网络系统一次、二次功率—频率变化情况如图4 所示。当负荷增加时，TVSG 控制调整逆变站输出功率，系统从稳定运行点A点到C点，频率从额定频率fref到f1不能回到额定频率值，属于一次调频。

图4 系统一次、二次调频曲线图Fig.4 Primary and secondary frequency regulator curves of the system

由式（4）可知，无源网络要实现无差控制，即Δf=0，则功率变化量需要满足ΔPe=ΔPL。本文引入功率差和直流电压偏差，作为TVSG 的前馈环节，设计出一种VFR频率控制策略，让运行点从A点移动到D点，系统就可以实现无差频率控制，其表达式为

3 VFR 无差调频特性以及调压特性分析

3.1 Ki和Kp参数对控制系统影响分析

根据图5 得到控制器中ω到ωref闭环传递函数为

图5 VFR控制原理图Fig.5 Schematic diagram of the VFR control

该控制器引入了积分参数Ki，因此需要对Ki参数对于控制系统的稳定性进行分析。

本文阻尼系数根据电网电压频率变化1 Hz，逆变器输出有功功率变化100%（即200 MW）选取[16]，阻尼系数根据下式进行合理的选取：

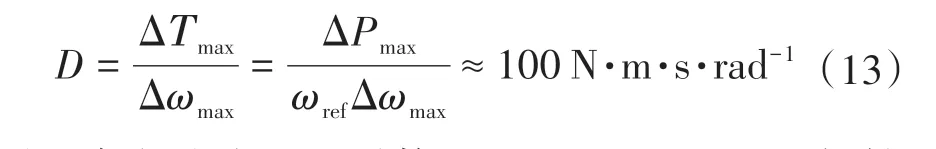
因此本文选取阻尼系数D=100 N·m·s·rad-1、惯性系数J=1 kg·m2以及PI环节比例系数Kp=50。

根据式（11）可变换以Ki为增益的传递函数如下

Ki取值范围大于0时绘制根轨迹如图6所示。分析Ki参数变化，控制系统的一对共轭特征根λ1，λ2一直在左半平面移动，所以Ki参数不影响控制系统的稳定性，综合考虑本文Ki取值为1。

图6 Ki变化时系统的根轨迹图Fig.6 Root locus of the system when Ki changes

以比例参数Kp为变量，绘制其根轨迹如图7所示。

图7 Kp变化时系统的根轨迹图Fig.7 Root locus of the system when Kp changes

控制系统的一对共轭特征根λ1，λ2一直在左半平面移动，不影响原本控制系统的稳定性；当Kp取值越大的时候，根轨迹的特征根靠近零点，系统的暂态稳定性变差。综合考虑本文Kp取值为50。

3.2 ku参数对控制系统影响分析

对式（7）进行变换得到频率增量Δω和直流电压增量ΔUdc之间的传递函数为

绘制以比例系数ku为变量的控制系统根轨迹。当ku＞0 时，Gu（s）的根轨迹如图8 所示，控制系统的特征根为非正，系统属于稳定状态；当ku＜0 时，Gu（s）的根轨迹如图9 所示，控制系统的特征根含有正数，控制系统属于不稳定状态。

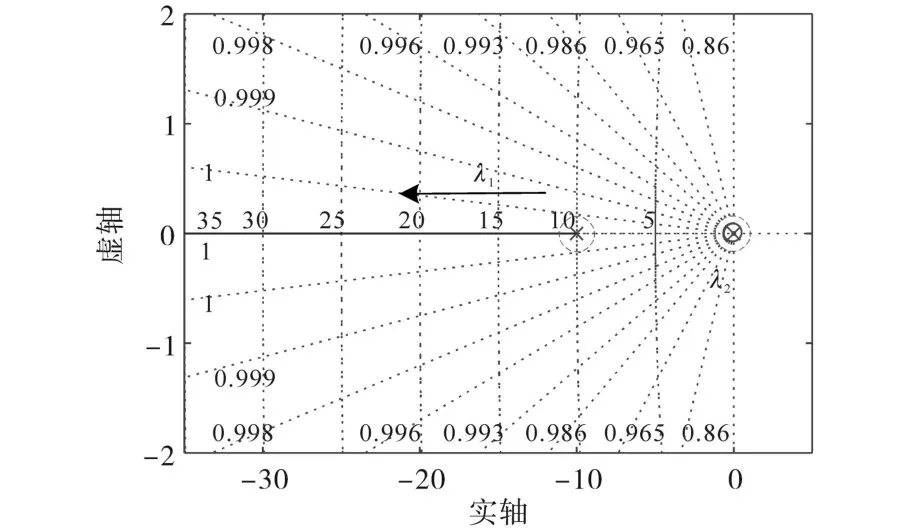
图8 ku大于0时系统的根轨迹图Fig.8 Root locus of the system when ku＞0

图9 ku小于0时系统的根轨迹图Fig.9 Root locus of the system when ku＜0

通过以上分析比例系数ku应当取为正值，本文ku取值为0.08。

4 仿真验证

本文在仿真软件PSCAD/EMTDC 搭建图1 所示的仿真模型。直流线路按照单位长度直流电阻为0.01 Ω/km，其中线路长度L1=60 km，L2=80 km，L3=60 km，L4=100 km。换流站1～4 的额定容量分别为400 MW，400 MW，500 MW，300 MW。

四端柔性直流输电系统的主要参数如下：直流电压200 kV，换流站1 下垂系数0.16，换流站1 功率220 MW，换流站2定功率280 MW，换流站3 下垂系数0.12，换流站3 功率300 MW；换流站4 控制器参数如下：阻尼系数D=100 N·m·s/rad，转动惯量J=1 kg·m2，下垂系数ku=0.08，频率无差调节比例系数Kp=50，频率无差调节积分系数Ki=1。向无源网络供电的U—f控制，即定交流电压控制，其结构如图10 所示，外环为定交流电压控制器，频率由压控振荡器给出。Usdref，Usqref分别为交流电压d，q轴参考值。外环PI 参数Kp1=2，Ki1=0.02；内环PI参数Kp2=60，Ki2=0.002。

图10 U—f控制器Fig.10 Controller of U—f

为了验证所提出的虚拟同步机控制方法有效可行、能为受端无源网络系统提供必要的频率支撑、能加强系统动态稳定性能，本文针对图1 中的换流站4 分别采用U—f控制、传统的虚拟同步机控制和本文提出的VFR 控制方法进行对比验证。

4.1 负荷阶跃响应

在1.5 s 时，换流站4 连接的交流侧负荷功率由200 MW突增至220 MW，运行至3 s时负荷功率突降至180 MW，系统响应仿真曲线如图11所示。

从图11a、图11b 可知，在1.5 s 时，VSC4交流侧负荷突增，直流系统出现功率缺额，导致直流电压出现下降，无源孤岛系统交流频率出现下降。在3 s 时，VSC4交流侧负荷突减，直流系统出现功率盈余，导致直流电压上升，无源孤岛系统交流频率上升。通过VSC1和VSC3采用功率-电压下垂控制来分担直流电网内不平衡功率。对比图11 a 的三种控制情况，当采用U—f控制时，负荷改变时频率出现大的波动，频率变化幅值大；当采用TVSG 控制时，由于转动惯量和阻尼系数的存在，孤岛系统的频率与额定频率差值减少，但属于一次调频；当采用VFR 控制VSC4时，VFR 控制参与孤岛系统二次频率调节，在受到负荷波动后可以恢复到额定频率。

从图11c 可知，在1.5 s 时，VSC4交流侧负荷突增，导致孤岛系统的交流电压出现了短暂的下降，采用VFR 控制策略，交流电压波动最小，孤岛系统电压更快恢复到额定电压值。从图11c 可知，在3 s 时，VSC4交流侧负荷突减，导致孤岛系统的交流电压出现了瞬时上升，采用VFR 控制策略，交流电压波动小，孤岛系统电压更快稳定恢复到额定电压值。

图11 负荷阶跃响应系统仿真曲线Fig.11 Simulation curves of load step response system

从图11d 可以看出，在1.5 s 时，负荷突增，VSC4缓慢增加吸收的功率VSC3相应减小吸收的功率；在3 s 时，负荷突降，VSC4缓慢减小吸收的功率，VSC3适当增加吸收的功率。采用VFR 控制各个换流站的有功功率更快恢复稳定性，体现出了VFR 控制策略为孤岛系统提供惯性支撑作用。

4.2 三相瞬时故障

孤岛系统交流线路在2 s 时，发生0.1 s 的瞬时三相接地短路故障。系统的动态响应如图12所示。从图12a 可知，采用U—f控制时，故障后孤岛系统的频率瞬间增大，出现频率尖峰；采用TVSG 控制方式下系统在发生故障的瞬间受端系统频率波动幅度较大，稳态恢复时间较长；采用VFR 控制方式下系统发生故障瞬间受端系统频率波动较小，稳态恢复过程较为平缓，快速回到额定频率值。