基于气隙磁链矢量的含DFIG直流系统功角控制

陆怡冰，李峰，赵文彬，卢武，霍思敏

（1.上海电力大学电气工程学院，上海 200090；2.国网湖南省电力有限公司，湖南长沙 410004）

近年来，基于双馈感应发电机（doubly fed induction generator ，DFIG）风电场的直流输电越来越受到广泛关注[1]。在已有的DFIG 连接直流（direct current，DC）电网的拓扑中，DFIG 通过二极管桥接在直流电网上的方式，因其定子侧结构简单、变流器成本小而受到广泛地关注和研究，也被称为DFIG-DC 系统，但传统基于锁相环的矢量控制策略无法应用，这是因为DFIG-DC 拓扑中不存在交流电网，且需要额外控制定子频率，因此，这种拓扑结构的主要目标是实现对定子频率和输出功率的精确控制[2]。然而，其面临的基本问题是如何在参数依赖性尽可能小的情况下获得定子频率和定向角[3]。

目前已有许多文献提出了适用于DFIG-DC系统的控制策略[4]。如定子频率和功率的解耦控制主要通过定子磁链定向控制来实现。在这些方法中，定子频率和定子磁链角是必不可少的解耦控制参数。根据获取定子频率和定向角的方法，已有的方法一般可以分为两类：电压型和电流型。文献[5]通过建立基于定子电压模型得到了定子频率和定子转矩角。文献[6]中定子频率和定子磁通角是直接根据定子磁通计算的，而定子磁通角与电阻参数有很大的关系。此外，定子的磁通角是定子电压的积分，由于不可避免的直流采样偏差，在实际应用中很难实现。文献[7]将积分链路被惯性链路代替，可以减少直流采样偏差的影响，但不能消除直流采样偏差的影响，这会在定向角上造成基频纹波。文献[8]通过基于电流模型获得定子频率和定子磁通角。文献[9]中定子磁链的大小用于定子的频率控制，它取决于定子的电感和互感。文献[10]通过控制q轴定子磁链为零来获得定子频率和定子磁链角，既避免了计算过程，也不依赖于定子电感和互感比值。当DFIG-DC 系统单机运行时，直流电压也通过定子磁链方向进行控制。

综上所述，现有的基于定子磁链定向控制的方法都不能避免直流偏置问题或参数依赖性问题[11-14]。由于DFIG 的定子侧不存在交流电网，且直流电网不存在无功功率，因此，这种拓扑结构不需要定子磁链定向控制以及定子频率和功率的解耦控制。与现有的DFIG-DC 控制方法完全不同的是，定子频率与定子功率不解耦通过d-q轴控制转子电流，可建立定子功率与气隙电动势角的关系[15]。定子功率不受有源轴上转子电流的控制，而是受气隙电压与定子侧电压夹角的控制[16]。因此，在定子有功功率控制回路的基础上可确定定子频率和定向角，避免了电压模型和电流模型的影响。通过控制q轴激励电流为零，实现了气隙磁通定向。通过对气隙磁通矢量的调节，可以实现对定子频率和定子有功功率的精确控制，且不存在参数依赖性，避免了采样偏置问题。由于定子电压高度畸变，谐波电流会引起转矩脉动，应加以抑制。文献[17]提出了抑制转矩脉动的预测控制方法。然而，这类文献只是针对转矩纹波的抑制，没有考虑定子和转子绕组中的谐波电流。文献[18]提出了一种改进的直接谐振控制方法，在抑制转矩脉动的同时降低谐波电流。由于转子与气隙磁链矢量是同轴的，因此改进的直接谐振控制方法仍然适用于该新型控制方法，可以同时缓解转矩脉动和谐波电流。总之，这种新的频率功率控制方法可以避免参数依赖性。此外，所有现有的改善性能的直接谐振控制仍然可以直接应用。

1 DFIG直流系统结构与模型

图1为DFIG直流系统一般结构图。

图1 DFIG-DC系统结构图Fig.1 The structure diagram of the DFIG-DC system

图1中，Usabc为定子电压，Vdc为直流端口电压，idc为直流侧电流。DFIG向直流电网发电的工作原理为：首先通过转子侧变流器（rotor side converter，RSC）将转子侧的激励电流注入转子绕组，然后建立气隙电动势。当相-相气隙电动势峰值高于直流电压时，二极管桥通，DFIG 向直流电网注入功率。发电机模式定义依据定子电流和转子电流的参考方向。根据同步d-q参考系下DFIG 的等效电路，可以得到气隙磁通矢量为

从气隙侧看，DFIG-DC 系统的稳态等效电路如图2所示。

图2 DFIG-DC系统稳态等效电路Fig.2 Steady-state equivalent circuit of the DFIG-DC system

图2 中，Rs为定子电阻，Lσs为定子漏感。当二极管桥工作在连续导通模式时，定子电压为三步方波，定子基电压的幅值可计算为

由式（3）可知，由于直流环节电压是恒定的，所以定子基电压是一个定值。因此，在忽略谐波的情况下，定子电压可以被认为是一个恒定的电压源。定子电阻与漏感电阻抗相比要小得多，可以忽略不计。从DFIG 传递到直流电网的功率如图3a所示，相量图如图3b 所示，相量图在同步dq坐标系中。

图3 DFIG-DC系统的等效相量图Fig.3 Equivalent phasor diagram of the DFIG-DC system

定子基电压矢量与气隙电动势矢量之间的相角为δ。此外，由于二极管桥接，定子基流矢量与定子电压矢量相位相同。气隙电动势矢量幅值为Em，因此，可计算出DFIG 向直流电网传递的定子有功功率为

由气隙磁通的叉乘和转子电流的共轭可计算转矩：

式中：Ird，Irq分别为d，q轴转子电流。

定、转子电流中同时存在谐波成分，导致转矩脉动。

2 所提控制策略及稳定性分析

2.1 控制系统设计

由于直流电压是恒定的，RSC 的控制目标是实现对直流电网输出功率的精确调节。此外，DFIG的定子频率不受交流电网的影响，交流电网也需要对其进行控制。定子功率和定子频率调节的RSC 控制方案如图4 所示，其主要包括定子功率控制、定子频率控制、气隙磁通定向和电流控制。

图4 功率频率调节RSC控制方案Fig.4 RSC control scheme for the power and frequency regulation

图4中，电流控制是内环控制回路，与传统的电流控制相同，定子功率控制、定子频率控制和气隙磁通定向、改进后的直接谐振控制等，在这里不再赘述。

由式（4）可知，定子功率随角度增大而增大，由于角δ会随着定子频率的升高而增大，因此定子频率可以由功率控制回路所产生：

式中：kpf和kif分别为q轴励磁电流控制器的比例、积分增益。

由于气隙磁通矢量指向d轴，定子磁通大小可近似计算为

式中：kpf，kif分别为定子频率控制器的比例、积分增益，这两个环与q轴励磁电流控制器相同，因为这两个环都是产生转子电流参考的外环；上标“*”为参考值。

本文所使用的谐振控制器的传递函数可以表示为

2.2 控制系统稳定性分析

图4为转子侧变流器的控制方案，由图可知，定子频率和定子功率为非解耦控制。定子频率由功率控制回路获得。因此，为了分析功率控制回路和定子频率控制回路的控制性能和稳定性，需要将二者结合起来考虑。由式（4）可知，定子有功功率可表示为定子电压和d轴转子电流：

由式（17）可知，定子功率既与d轴转子电流有关，又与角度δ有关。这两个因素对定子功率的影响可以用偏导数表示为

由于转子电流控制的内环比功率控制的外环快，可以将其简化为一个单位增益块。式（20）与式（21）相结合，功率控制回路框图如图5所示。

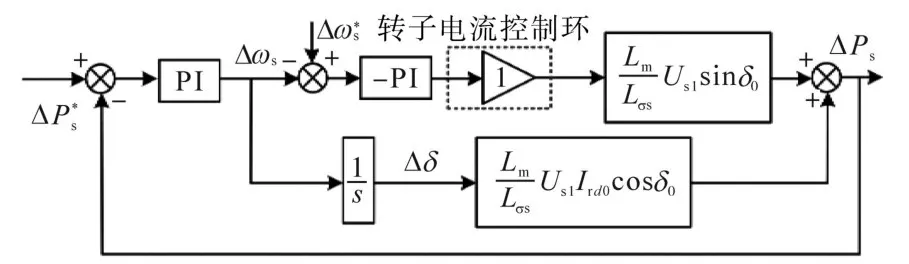
图5 功率和定子频率控制回路框图Fig.5 Block diagram of the power and stator frequency control loop

由于角度δ的范围是相当小接近零，故sinδ在整个功率范围内近似为零。由图5 可知，可以消除定子频率控制对功率控制的影响。因此，设计功率控制的运行点是零输出功率，这意味着角度δ为零，sinδ为零。这样可以简化功率控制回路，如图6所示。

图6 简化后的功率控制回路方框图Fig.6 Block diagram of the simplified power control loop

定子功率控制回路的传递函数可通过推导得到：

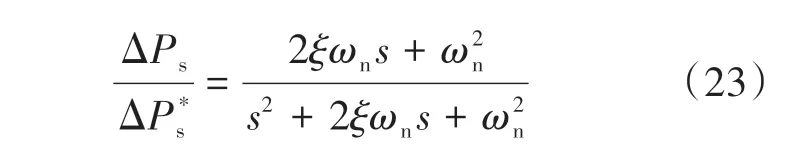
式中：ξ为阻尼比；ωn为额定角频率。

由式（23）可知，功率回路的传递函数为二阶系统。根据二阶系统的设计原理，阻尼比ξ通常设为0.707，并根据功率控制要求设计带宽。本文将定子功率控制的带宽设计为10 Hz。因此，将ωn设为20π rad/s。功率控制回路的比例参数kpp为0.29，积分参数kip为126。将定子频率控制回路的比例参数kpf和积分参数kif分别设置为1 和80。图7 为定子功率从0（标幺值）升至1（标幺值）的根轨迹图。左边小于1 的数字表示阻尼比。

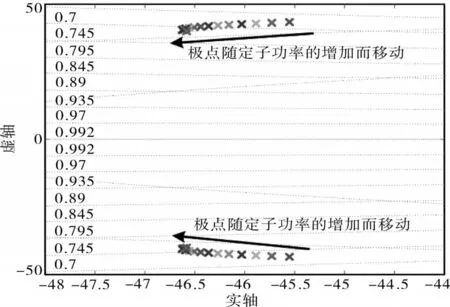
图7 定子功率和频率控制回路的根轨迹Fig.7 Root locus of the stator power and frequency control loop

由图7可知，随着定子功率的增加，极点向左移动，且所有极点都位于左半平面内，表明功率和定子频率控制回路始终稳定。此外，磁极随定子功率的变化不明显，说明系统运行点对功率控制性能的影响不大。

当气隙磁通矢量指向d轴时，q轴气隙磁通Ψmq0为零。因此，式（6）中的转矩表达式可以表示为

式中：Isd6为d轴上的六阶定子谐波电流。

由于定子谐波电流与转子谐波电流呈线性关系，因此可以采用谐振控制器对转子谐波电流进行控制，说明谐振控制器也可以直接对定子谐波电流进行控制。因此，d轴定子谐波电流和转矩脉动可以作为一种新的复杂变量组合在一起。新复变量的直接谐振控制可表示为传递函数，如图8所示。

图8 改进的直接谐振控制方框图Fig.8 Block diagram of improved direct resonant control

图8 中的复传递函数是根据DFIG 模型得到的，可以表示为

式中：Ls为定子电感；Rr为转子电阻。

由传递函数Gp（s）可以看出，由于式（16）中耦合项作为前馈加入到转子电压中，所以分母中不存在耦合项。

3 仿真分析

为了验证所提控制策略的有效性，本文的实验系统结构图，如图9 所示。DFIG 由鼠笼式感应电动机和普通电动机驱动。

图9 实验系统示意图Fig.9 Schematic diagram of the experimental system

直接谐振控制策略在TI TMS320F28335 DSP上实现，开关频率为10 kHz，采样频率为10 kHz。DFIG 的参数设置如下：额定功率1.0 kW，额定频率50 Hz，极对数3，Rr=0.88 Ω，Ls=5.6 mH，额定电压110 V，直流电压140 V，Rs= 1.01 Ω，Lm=87.5 mH，Lr= 5.6 mH。所有波形均由YOKOGAWA DL750示波器采集。

转子电流中带有直流采样偏移的定子磁通定向控制实验结果如图10所示。定子功率参考值为400 W，定子频率参考值为50 Hz，转子转速为800 r/min。因此。转子电流中的直流偏移量表示为同步d，q轴上10 Hz的脉动分量，在定子功率和转矩上产生10 Hz 的脉动。从图10 结果可以看出，定子电流包络线在10 Hz处振荡，定子功率和转矩的10 Hz 波动甚至高于需要抑制的300 Hz 波动。随后，在实验系统中，采用了新的功率频率控制方法。

图10 带直流偏置的定子磁链定向控制的实验结果Fig.10 Experimental results of the stator flux orientation with DC offset

图11 为定子有功参考功率从200 W 变化到800 W时DFIG的阶跃响应实验结果。

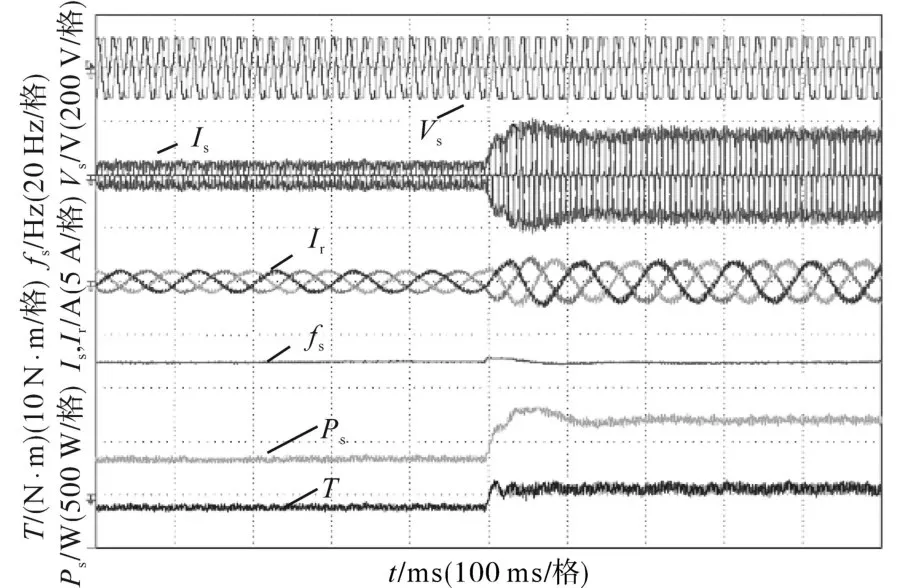
图11 功率从200 W变化到800 W时DFIG的阶跃响应Fig.11 Step response of DFIG when power change from 200 W to 800 W

图11 中，转子转速为800 r/min，定子频率设置为50 Hz。定子有功功率在二阶系统中有一点超调。另外，该方法可以在不存在稳态误差的情况下，在110 ms 内准确跟踪功率基准，验证了定子功率控制回路的有效性。从图11 实验结果可以看出，10 Hz 的波纹被消除。定子频率由50 Hz变化至60 Hz 时的阶跃响应，如图12 所示。定子功率参考值为500 W。在定子频率变化过程中，由于定子磁链的瞬态作用，使定子功率产生脉动，在50 ms 内达到稳定状态。定子频率可在10 ms内快速跟踪基准频率，且无超调，验证了定子频率控制回路的有效性。

图12 定子频率变化范围为50 ～60 Hz时的阶跃响应Fig.12 Step response when stator frequency change from 50 Hz to 60 Hz

图12 左半部分的放大图如图13 所示。定子频率设置为50 Hz，定子功率设置为500 W。由于定子侧二极管桥，定子电流受到五次谐波和七次谐波的严重畸变，五次谐波和七次谐波分别为23.7%和6.4%。300 Hz 的转矩脉动为6.8%，对DFIG的机械轴是有害的。因此，有必要采用改进的直接谐振控制来减轻谐波电流和转矩纹波。

图13 无改进直接谐振控制的稳态结果Fig.13 Steady-state results without improved direct resonant control

改进后的直接谐振控制稳态结果如图14 所示。第五次谐波和第七次谐波电流都大大降低到2.3%和5.8%。由于减小转矩脉动所必需的谐波电流，谐波电流不能被完全抑制。300 Hz 的转矩脉动也降低到0.93%。因此，改进后的直接谐振控制仍然可以直接应用于新型定子频率和功率控制中，具有简单、有效的消除转矩脉动和谐波电流的效果。通过减小定子谐波电流，降低了DFIG的运行损耗，提高了DFIG-DC系统的运行效率。

图14 改进的直接谐振控制的稳态结果Fig.14 Steady-state results with improved direct resonant control

4 结论

本文提出了一种基于气隙磁链定向的DFIG-DC 系统定子功率和定子频率控制新方法。采用定子功率控制回路来产生定子频率和定向角，而不是采用电压模型或电流模型来获取定子频率和定向角，避免了参数依赖和直流采样偏移的影响。通过控制q轴激励电流为零来实现气隙磁通定向。此外，还可以直接采用改善后的直接谐振控制来减轻转矩脉动和谐波电流，这表明新提出的控制策略适用于所有现有的抑制谐波或提高效率的改进控制策略。该控制策略在不影响现有控制性能的前提下，减少了参数依赖性。