颗粒增强金属基复合材料细观有限元建模方法的对比

刘骏华，张 娟，张 晨，黄兴民

(西南交通大学1.力学与航空航天学院，应用力学与结构安全四川省重点实验室;2.材料科学与工程学院，成都，610031)

0 引 言

颗粒增强金属基复合材料具有较高的强度、弹性模量、硬度以及良好的塑性，并且生产成本低廉，应用前景广泛。颗粒增强金属基复合材料在承受载荷时的变形与失效等行为是非常复杂的，与基体和颗粒两相材料的性能以及二者之间的多种相互作用密切相关。在研究微观及细观结构对复合材料力学性能的影响中，采用有限元方法进行数值模拟是一种非常有效的手段。想要进行有效的模拟，必须先要建立合理的细观有限元模型。目前，颗粒增强复合材料的细观有限元模型主要有体胞模型和真实结构模型2种。体胞模型的构建基于复合材料的结构特征，可分为单颗粒模型及多颗粒模型[1-2]。单颗粒模型由于其结构简单，常用其来揭示基体、颗粒及界面之间的作用机理，但无法探究颗粒之间的相互关系[3]。对于多颗粒模型，可以假设颗粒是均匀分布的，也可以使用随机序列吸附法生成随机分布多颗粒模型[4]。随机分布多颗粒模型相比于单颗粒模型虽然考虑了颗粒间的相互作用，并且一定程度上考虑了材料的不均匀性，但与复合材料的真实微观结构还有一定差异[5]。研究[6]表明，颗粒形貌越接近实际情况，模拟结果与试验结果的误差越小，因此有学者发展了基于材料真实显微图像的建模方式，即真实结构模型。真实结构模型一般使用连续切片法建立，其原理是将试样分成很多层，取得每一层的平面结构图像并输入计算机中，然后利用三维重构技术，还原出试样的三维真实结构[7]。由于三维真实结构模型的建立需要复杂的前期工作并且伴随着庞大的计算量，因此有不少学者建立了二维真实结构模型进行模拟，得到的模拟结果与试验结果吻合得较好[8-11]。

体胞模型和真实结构模型各有特点，在模拟颗粒增强复合材料的力学行为时得到的结果也有差异，为了探究这2种模型的异同及特点，作者以原位生成法制备的TiB2颗粒增强铁基复合材料为研究对象，通过纳米压痕试验及有限元反演分析确定了铁素体基体的幂硬化模型参数，建立了二维的颗粒随机分布的体胞模型和真实结构模型，模拟材料在单轴拉伸时的力学行为，研究了2种模型有限元模拟结果的异同，并进一步探究了边界条件对模拟结果的影响，以期在一定程度上为颗粒增强铁基复合材料微观结构的优化设计提供参考。

1 有限元模型的建立

1.1 材料参数的确定

在有限元建模的过程中，需要输入复合材料各相的材料参数。在采用原位生成的方法制备的TiB2颗粒增强铁基复合材料中，铁素体晶粒尺寸与纯铁中的铁素体晶粒尺寸不同，而且晶粒中会有位错产生[12]，这导致复合材料中的铁素体与纯铁中的铁素体在未受载时的初始状态可能会有较大不同。若采用纯铁进行单轴拉伸试验来获得复合材料铁素体基体的参数不合理，因此采用纳米压痕和有限元反演分析的方式获得铁素体基体的材料属性。将TiB2颗粒视为弹性体，弹性模量为510 GPa，泊松比为0.25。对TiB2颗粒增强铁基复合材料进行纳米压痕试验，测得基体的弹性模量为214 GPa，硬度为4.01 GPa，然后进一步采用DAO等[13]推导的量纲函数及有限元反演分析，确定基体的单轴幂率硬化应力-应变响应曲线。假设基体的应力σ、应变ε满足以下关系：

(2)

式中：E为基体的弹性模量；σy，εy分别为名义屈服强度与对应的名义屈服应变；εp为总应变减去名义屈服应变；n为幂硬化指数；σr、εr分别为特征应力与特征应变。

将纳米压痕试验中采用的Berkvich压头等效成140.6°的圆锥压头，建立轴对称纳米压痕有限元模型[14]。参考ANTUNES等[15]和LEE等[16]的研究方法进行有限元反演，得到铁素体基体的单轴真应力-真应变曲线如图1所示，铁素体基体的幂硬化指数n为0.34，屈服强度σy为242.91 MPa，且由图2可以看出，采用有限元反演分析方法得到压痕试验过程中的力-位移曲线与试验结果相吻合，验证了有限元反演分析方法的准确性。

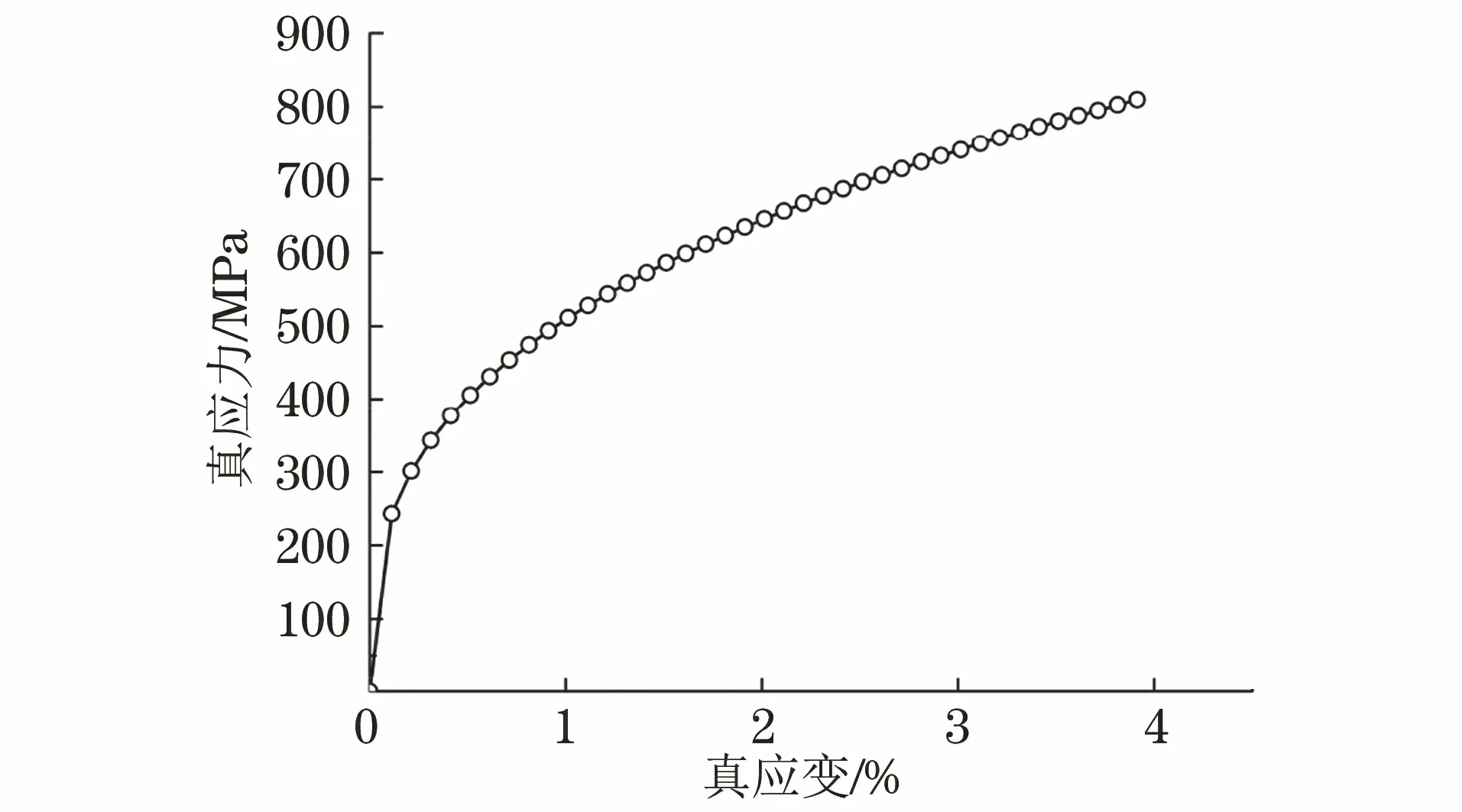
图1 采用有限元反演分析得到铁素体基体的真应力-真应变曲线Fig.1 True stress-true strain curve of ferrite matrix by finite element inverse analysis

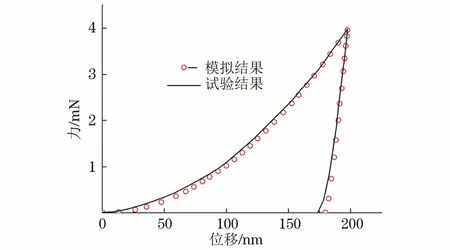
图2 有限元反演分析方法得到压痕试验过程中的力-位移曲线与试验结果的对比Fig.2 Comparison of force-displacement curves during indentation test obtained by finite element inverse analysis with experimental results

1.2 有限元模型的建立

对体积分数20% TiB2颗粒增强铁基复合材料建立二维代表性体积元模型。研究[11]表明，当所选取的代表性体积元尺寸大于某一临界值时，其所代表的微结构能够反映材料微观组织的基本信息。所选取的真实结构模型尺寸为80 μm×80 μm。在复合材料的扫描电镜(SEM)形貌中选择尺寸为80 μm×80 μm合适区域，经二值化处理转化为矢量文件，然后导入ABAQUS软件中进行建模，实现基于微观组织的有限元模型的建立，如图3所示。测得所选区域真实颗粒的平均尺寸为3 μm。

图3 真实结构模型建立的3个阶段Fig.3 Three stages of establishing real structure model: (a) SEM micromorphology; (b) results by binarization and (c) geometric model

体胞模型代表性体积元的建立则利用ABAQUS软件进行二次开发，采用Python语言编写程序，运行程序建立同等颗粒尺寸、体积分数的随机分布圆形颗粒及不规则颗粒的体胞模型，如图4所示。

图4 随机分布圆形颗粒及不规则颗粒的体胞模型Fig.4 Body cell models of circular particles with random distribution (a) and irregular particles with random distribution (b)

在ABAQUS软件中进行有限元模拟，将TiB2颗粒设为弹性体，采用CPS4R单元划分网格，平均单元尺寸为0.4 μm。代表性体积元模型一般可施加3种边界条件[17]，即同质化边界条件、对称性边界条件和周期性边界条件，如图5所示。

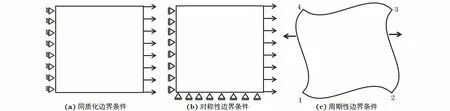
图5 建模可选择的3种边界条件Fig.5 Three alternative boundary conditions for modeling: (a) homogenization boundary condition; (b) symmetric boundary condition and (c) periodic boundary condition

1.3 应力-应变曲线的模拟及试验验证

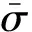
(4)

式中：A，σij，εij分别为单元面积、应力、应变。

根据上述公式编写Python脚本得到采用一阶均匀化方法计算的真应力-真应变曲线。等效宏观方法将代表性体积元等效成宏观模型，在对模型进行单向拉伸加载时，直接输出拉伸方向的作用力和位移，然后除以模型的横截面积和长度，得到工程应力-应变曲线再转化为真应力-真应变曲线。

按照GB/T 228—2010，在体积分数20% TiB2颗粒增强铁基复合材料上截取如图6所示的拉伸试样，用 MTS CMT5105 型电子万能试验机进行室温拉伸试验，拉伸速度为 1 mm·min-1。

图6 拉伸试样的尺寸Fig.6 Size of tensile specimen

将用施加对称性边界条件的真实结构模型和体胞模型模拟出的结果与单轴拉伸试验结果进行对比，结果如图7所示。由图7可以看出，采用2种方法得到不同模型的真应力-真应变曲线与试验结果较吻合，但采用等效宏观方法计算得到的真应力-真应变曲线与试验结果更加吻合，相对误差小于5%，因此后面采用等效宏观方法计算真应力-真应变曲线，同时也证明了建立的真实结构模型与体胞模型的合理性。

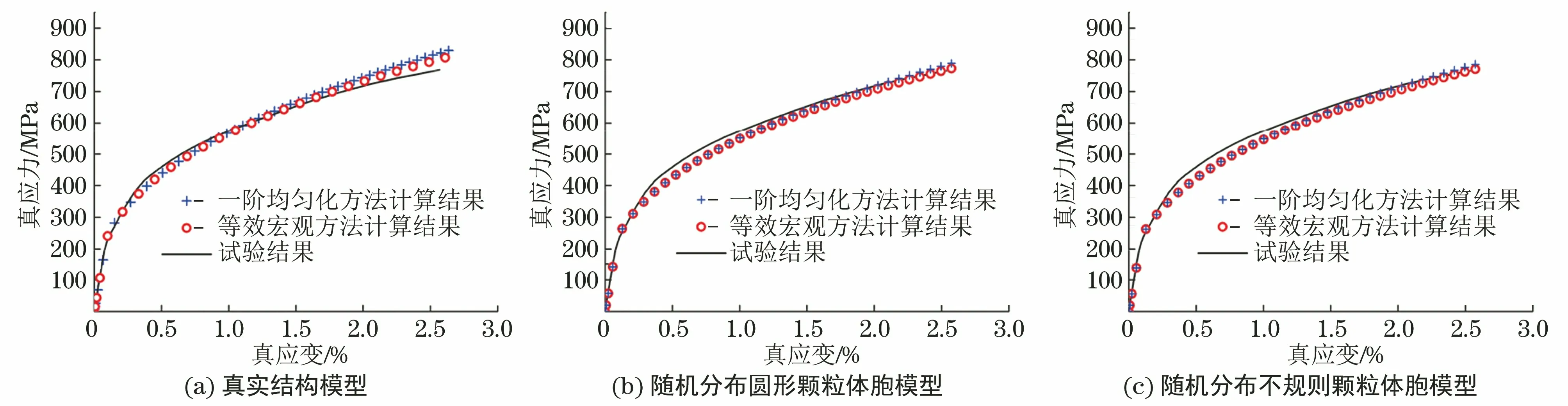
图7 对称性边界条件下由真实结构模型与体胞模型模拟得到数据经等效宏观方法和一阶均匀化方法计算得到真应力-真应变曲线与试验结果的对比Fig.7 Comparison of true stress-true strain curves calculated by equivalent macro method and first-order homogenization method from simulation by real structural model (a) and body cell model (b-c) under symmetric boundary condition with test results: (b) circular particle with random distribution and (c) irregular particle with random distribution

2 结果与讨论

2.1 边界条件对模拟结果的影响

在3种边界条件下用真实结构模型进行沿水平方向的单轴拉伸有限元模拟，得到的拉伸真应力-真应变曲线如图8所示。由图8可以看出，不同边界条件下模拟得到的真应力-真应变曲线基本重合，说明边界条件对模拟结果影响较小。

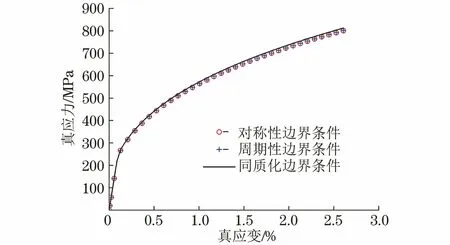
图8 不同边界条件下用真实结构模型单轴拉伸模拟得到的真应力-真应变曲线Fig.8 True stress-true strain curves obtained by simulating uniaxial tension with real structure model under different boundary conditions

由图9可以看出，边界条件对约束位置的应力、应变场具有一定影响，由于同质化边界条件和对称性边界条件对垂直加载方向的约束能力弱，使模型变形过程中沿垂直加载方向有一定的收缩，从而导致模型的最大应力与最大等效塑性应变位置具有较大的差异。周期性边界条件下模型变形均匀，在边界位置应力场连续性较好，与复合材料内部实际情况相吻合。对称性边界条件与周期性边界条件下的应力与应变云图有较高的相似性，因此单轴拉伸试验模拟时可用对称性边界条件代替周期性边界条件施加载荷。

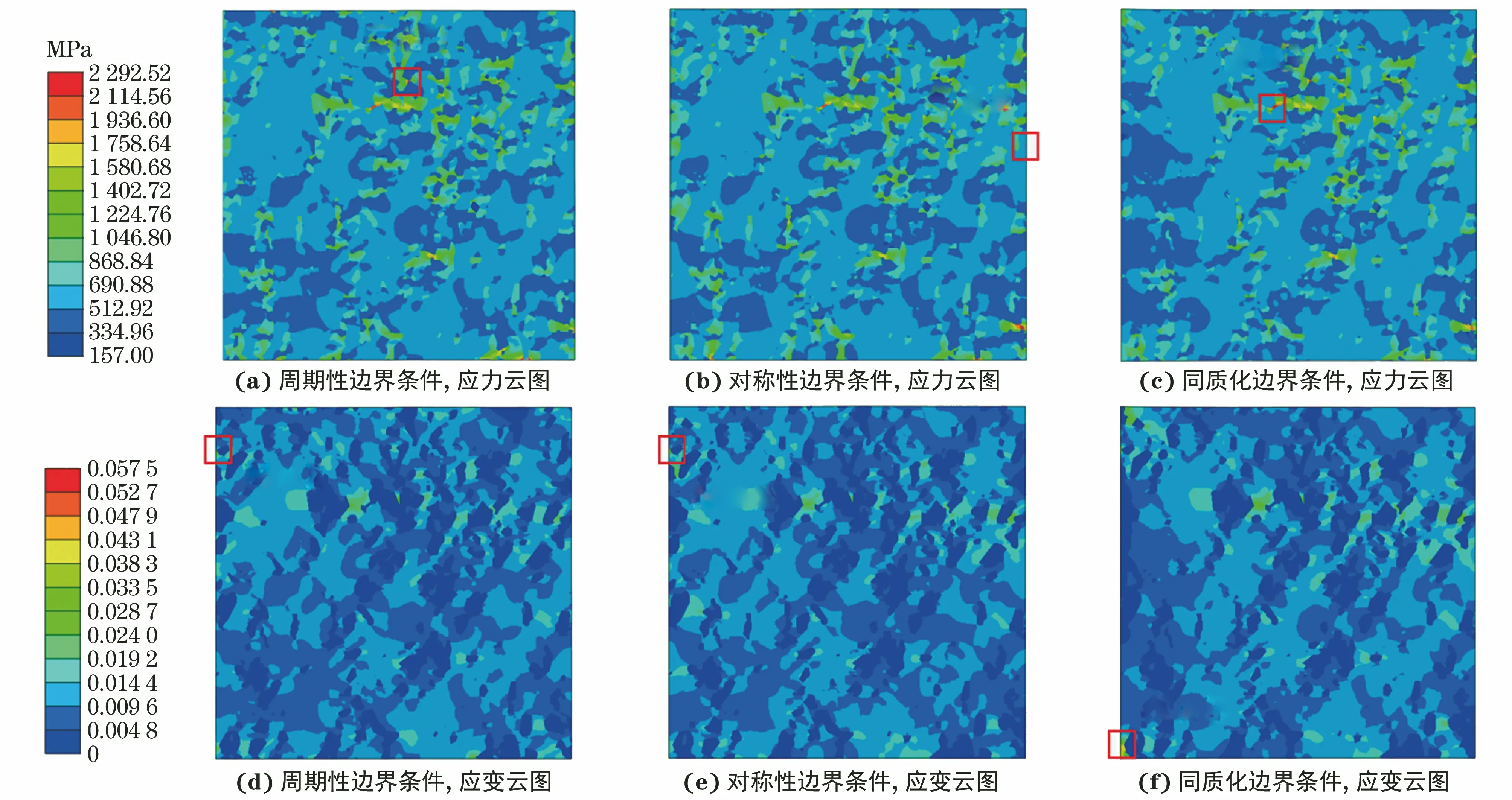
图9 不同边界条件下用真实结构模型模拟单轴拉伸真应变1%时的Mises应力云图和等效塑性应变云图Fig.9 Mises stress countour (a-c) and equivalent plastic strain countour (d-f) by simulating uniaxial tension with real structure model for true strian of 1% under different boundary conditions: (a,d) periodic boundary condition; (b,d) symmetric boundary condition and (c,f) homogenization boundary condition

2.2 2种建模方法下模拟结果的对比

由图10可以看出，对2种模型模拟单轴拉伸得到的真应力-真应变曲线间差异较小，且均与试验结果吻合较好，相对误差小于5%。根据真应力-真应变曲线计算得到的屈服强度及弹性模量如表1所示。

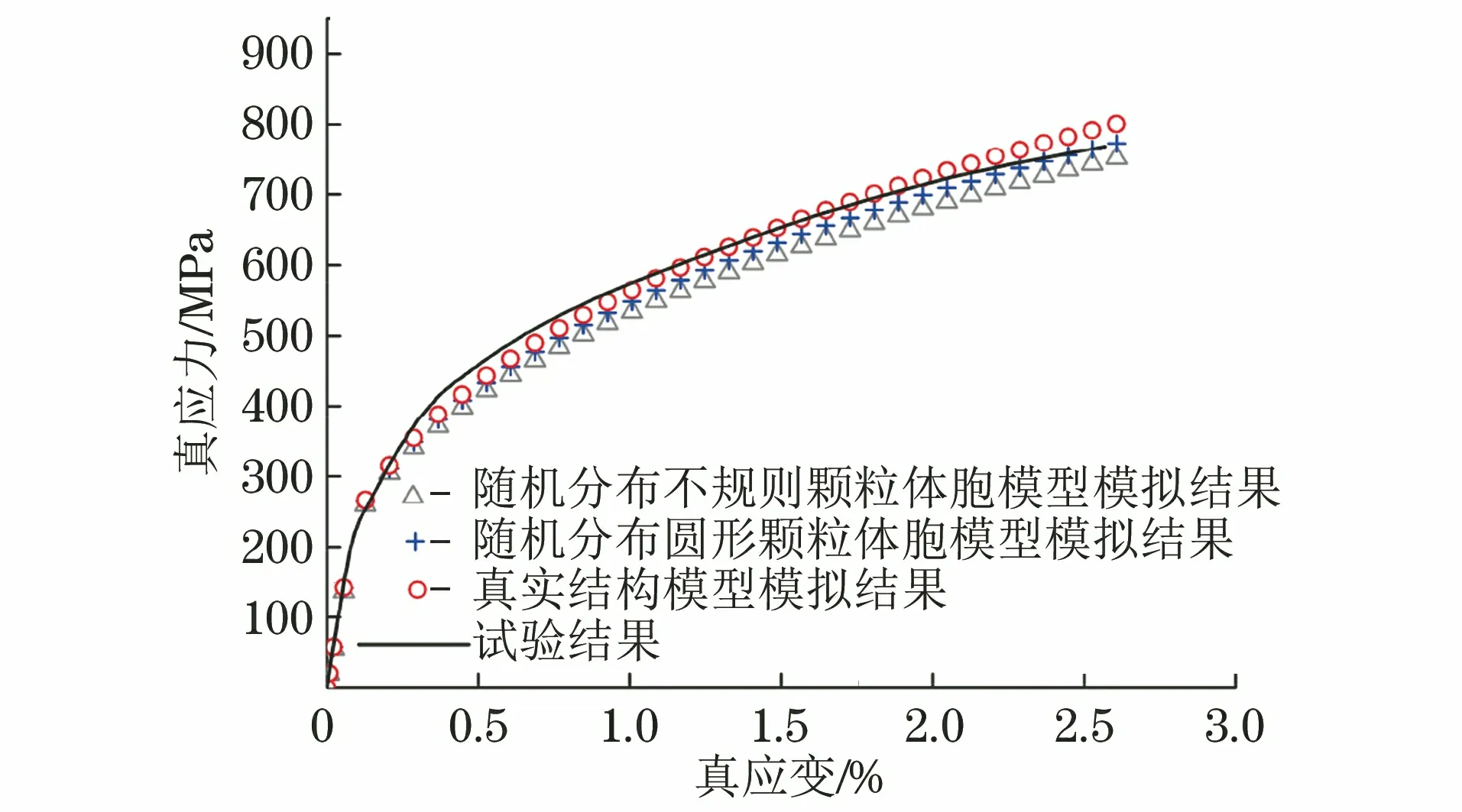
图10 对称性边界条件下用不同模型模拟单轴拉伸得到的真应力-真应变曲线与试验结果的对比Fig.10 Comparison of true stress-true strain curves by simulating uniaxial tension with different models under symmetric boundary condition with test results

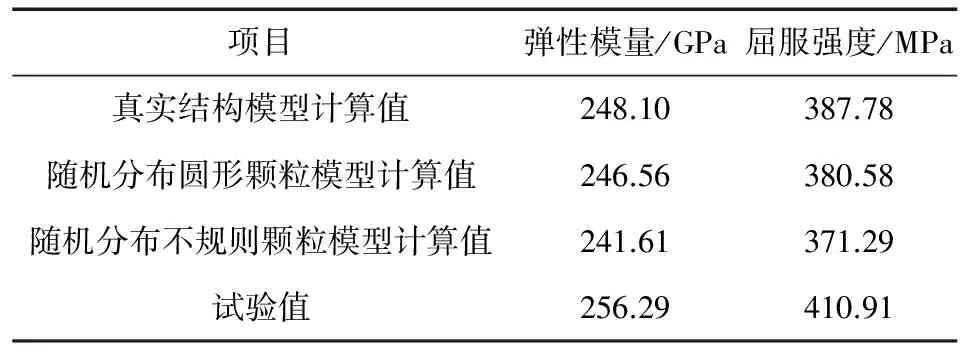
表1 对称性边界条件下用不同模型模拟单轴拉伸得到的弹性模量和屈服强度以及试验结果

由表1可以看出，对2种模型模拟单轴拉伸后得到的弹性模量及屈服强度与试验结果均相差较小，相对误差小于10%。从工程应用的角度来看，这两种模型都可以较好地模拟复合材料在单轴拉伸过程中的应力-应变曲线。对真实结构模型模拟单轴拉伸得到的弹性模量及屈服强度与试验结果间的相对误差最小，分别为3.19%与5.63%，说明真实结构模型在弹性模量及屈服强度模拟方面的可靠性更高。

由图11可以看出，颗粒分布与形状的不同导致基体和颗粒的应力场和塑性应变场具有明显的差异。体胞模型对颗粒的形状与分布进行了一定近似处理，而真实结构模型中的颗粒具有更多的棱角，颗粒与基体之间有较多的接触面积，因此相比于近似化的体胞模型其内部应力集中区域较多，这也是导致真实结构模型下在相同应变时的应力略高于体胞模型的原因。复合材料基体高应力区域多在沿加载方向的颗粒之间，并且颗粒间距越小，其中间的基体等效应力越大；不同模型中基体较大的等效塑性应变主要集中在高应力区域，并且等效塑性应变云图与各自的等效应力云图具有相似性；2种模型中颗粒的高应力区域多位于颗粒的尖角处和颗粒间距较小处。由表2可知：真实结构模型颗粒的最大等效应力分别为随机分布圆形颗粒体胞模型和随机分布不规则颗粒体胞模型的2.22倍和2.23倍；真实结构模型基体的最大等效塑性应变分别为随机分布圆形颗粒体胞模型和随机分布不规则颗粒体胞模型的1.38倍和2.58倍。由此可见，2种模型模拟颗粒增强金属基复合材料局部微观等效应力场及应变场的结果有明显差异，这是由于在颗粒增强金属基复合材料实际服役过程中，基体常因产生较大塑性变形而失效，而颗粒则容易在其高应力区域的尖角处发生断裂。因此，在对复合材料的断裂、失效等行为进行模拟时，真实结构模型和体胞模型的模拟结果会存在较大的差异。

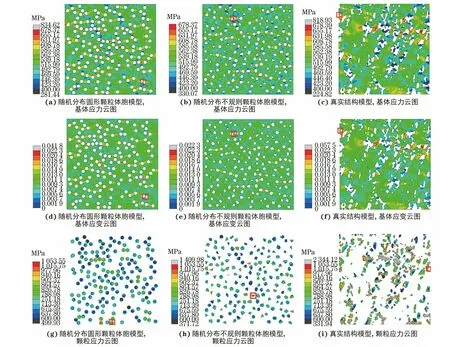
图11 对称性边界条件下用不同模型模拟单轴拉伸1%时基体的Mises应力云图和等效塑性应变云图以及颗粒Mises应力云图Fig.11 Mises stress countour (a-c) and equivalent plastic strain countour (d-f) of matrix (a-f) and Mises stress countour of particles (g-i) by simulating uniaxial tension with different models for true strain of 1% under symmetric boundary condition:(a, d, g) body cell model of circular particle with random distribution; (b,e,h) body cell model of irregular particle with random distribution and (c,f,i)real structure model

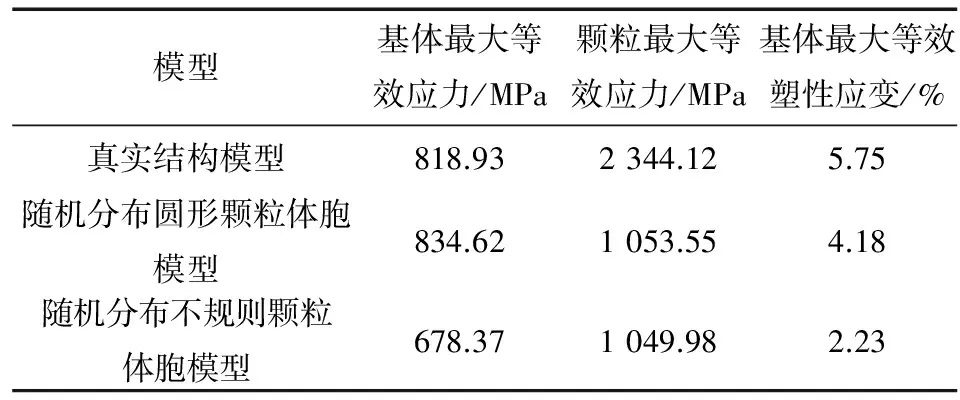
表2 对称性边界条件下用不同模型模拟单轴拉伸真应变为1%时基体的最大等效应力、最大等效塑性应变及颗粒的最大等效应力

3 结 论

(1) 对原位生成法制备的TiB2颗粒增强铁基复合材料建立了颗粒随机分布的体胞模型和真实结构模型，采用ABAQUS软件根据不同模型对单轴拉伸进行有限元模拟后，采用等效宏观方法获取的真应力-真应变曲线与试验结果基本吻合，相对误差小于5%，验证了这2种模型的合理性。

(2) 同质化边界条件、对称性边界条件和周期性边界条件下用真实结构模型模拟拉伸得到的真应力-真应变曲线基本重合，说明边界条件对模拟结果影响较小；对称性边界条件下的应力与应变云图与周期性边界条件相似，在单轴拉伸试验模拟时可用对称性边界条件代替周期性边界条件施加载荷。

(3) 用真实结构模型和体胞模型模拟单轴拉伸得到的真应力-真应变曲线间差异较小，且均与试验结果吻合较好，相对误差小于5%，得到的弹性模量及屈服强度与试验结果均相差较小，相对误差小于10%，且真实结构模型模拟单轴拉伸得到的弹性模量与屈服强度的误差小于体胞模型，说明真实结构模型在弹性模量及屈服强度模拟方面的可靠性更高。

(4) 用不同模型模拟得到复合材料基体与颗粒在单轴拉伸时的局部微观等效应力场及应变场有明显差异，真实结构模型模拟颗粒的最大等效应力分别为随机分布圆形颗粒体胞模型和随机分布不规则颗粒体胞模型的2.22倍和2.23倍，基体的最大等效塑性应变分别为这2种体胞模型的1.38倍和2.58倍。