基于深基坑变形控制机理的大跨度鱼腹梁支撑的设计方法
2022-08-04林焱林思远贾书岭
林焱,林思远,贾书岭
(1.中国路桥工程有限责任公司,北京 100011;2.上海强劲地基工程股份有限公司,上海 208106)
0 引言
城市高层建筑呈现密集化快速发展,地下空间及附属设施需求越来越多样化,临时性基坑作为岩土工程领域的一个综合性学科面临着前所未有的挑战,基坑支护体系设计阶段首要确保安全性,综合考虑施工工期、工程成本,选择最优的基坑支护方案显得尤为重要。近年来,传统的放坡、桩锚等支护体系在实际应用中很大程度上受到限制,内支撑式支护结构成为深基坑工程支护中备受青睐的首选,通常采用钢筋混凝土支撑或钢支撑结构作为支护体系。张颖等[1]研究了多圆环支撑结构在软土地区深基坑中的实践,表明圆环支撑相交布置可有效地增加无支撑空间,通过对大阳角处支撑结构的优化设计,减少了支护结构薄弱区域周边环境的变形。周臻等[2]提出免迭代法用于模拟预应力鱼腹梁时具有精度高、免迭代与操作简单的优势。黄天荣[3]分析了预应力鱼腹梁组合支撑较适用于严格控制变形的深基坑;旋喷加劲桩在条件允许、深度不大的大面积基坑开挖中具有明显优势。王寿生等[4]从不同角度将鱼腹梁支撑与传统支撑技术的特点进行对比剖析,预应力鱼腹梁装配式钢支撑技术具有良好的应用效果和市场竞争力。毕平均等[5]研究了鱼腹曲线模型、钢绞线数量、端部角度及跨度对鱼腹梁刚度的影响, 并给出鱼腹梁刚度的建议值。前人这些研究为鱼腹梁支撑设计理论完善与发展做出了积极贡献,但是对大跨度鱼腹梁支撑的研究尚无明确详细的研究文献,为此,本文基于深基坑变形控制机理对大跨度鱼腹梁支撑的设计方法进行了较为深入的研究。
1 深基坑变形控制机理
深基坑支护随着开挖深度的增加,施工难度增大,尤其在城市软土区域,周边建筑环境复杂,开挖过程中不仅要确保基坑自身的安全与稳定,而且要有效控制因开挖或降水导致的基坑周围地层发生过大的沉降变形,以减少对周边环境的影响程度。装配式预应力鱼腹梁钢结构支撑,将预应力引入能大幅度提高内支撑体系的抗变形刚度,节约了钢支撑的使用数量,基坑开挖作业空间也显著增加,相比传统支撑体系更为重要的是可以通过实时张拉钢绞线动态调整预应力,以达到对基坑变形主动控制的效果。
2 基坑变形与大跨度鱼腹梁支撑刚度的关系
对深基坑支护的要求越来越严格,其重点由强度控制转变为刚度控制[6],选择合理的基坑支护结构和支撑刚度才能够有效控制基坑变形,确保基坑安全。
2.1 大跨度鱼腹梁支撑与基坑变形分析模型
鱼腹梁结构是由上弦梁、腹杆、下弦拉索及支座组成。图1 所示为鱼腹梁支撑在均匀载荷q作用下的受力分析模型。

图1 大跨度鱼腹梁建模示意图Fig.1 Schematic diagram of modeling of long-span fish-belly beam
2.2 大跨度鱼腹梁支撑刚度对基坑变形的影响分析
根据均布荷载下梁跨中挠度相等原则,为便于计算将鱼腹梁支撑结构等效为等刚度梁构件,鱼腹梁支撑结构等效抗弯刚度为[7]:

式中:q为均布荷载;L为鱼腹梁跨度;w为结构跨中挠度;Ew为上弦梁的弹性模量,MPa;Iw为惯性矩,其中,Aw为上弦梁截面面积;Eg为钢绞线的弹性模量,MPa;Ag为钢绞线截面面积;f为鱼腹梁高度。鱼腹梁等效平均刚度为:

2.3 大跨度鱼腹梁的预应力效应对基坑变形的影响分析
基坑开挖前,通过对大跨度鱼腹梁支撑系统施加预应力,激发了坑外土体的被动土压力[8],有效地控制基坑开挖后挡土结构的受力和变形,大幅度提高了鱼腹梁支撑系统的刚度及稳定性。随着基坑开挖深度的不断增加,基坑变形逐渐增大累计近报警值时可通过预留的未张拉钢绞线进行多次预应力张拉,以动态化控制基坑周边土体的变形。
施加预应力对土体压缩变形的影响,假定支撑系统后面的土体符合Winkler 地基模型,均匀的土体施加外荷载P,可简化为水平方向上的一维压缩问题,支撑系统受到施加预应力后,产生反向变形来抵消结构受荷载后的部分变形,以减小支撑结构的总挠度,表现为提高了支撑系统的表观刚度。虽然其本身固有刚度不会改变,但表现出来的变形控制能力表明在支撑的固有刚度不变时,通过施加预应力能获得较高的表观刚度。
施加预应力后的跨中挠度[9]为:

式中:TP为鱼腹梁钢绞线施加预应力;X1′为多余未知力。
鱼腹梁的等效抗弯刚度:

式中:α为鱼腹梁端部钢绞线与上弦梁的夹角;λ为鱼腹梁结构高跨比;η为鱼腹梁钢绞线预应力系数。
3 大跨度鱼腹梁支撑刚度影响因素分析
3.1 高跨比对大跨度鱼腹梁支撑刚度的影响
大跨度鱼腹梁支撑结构,因其自身跨度较大,高跨比过小会造成结构的承载力不足,降低支护结构的稳定性;高跨比过大,会造成材料的浪费,同时减少了基坑开挖空间。合理的高跨比能使支撑结构既安全又经济。
从图2 可以看出,随着高跨比的增大,支撑结构的等效刚度逐渐增大,且支撑结构在高跨比1/10~1/6 范围的等效刚度变化斜率明显低于高跨比1/6~1/3 范围。

图2 等效刚度随鱼腹梁支撑高跨比的变化趋势Fig.2 The change trend of equivalent stiffness with the height-span ratio of fish-belly beam support
各种内力作用下可以反映构件性能的应力比率,以实际应力与允许应力的比值大于1,表明支撑结构构件处于不安全状态,当实际应力达到允许应力值时作为构件能够承受的极限荷载值。
钢材效率系数:

式中:F为极限荷载,kN/m;m为型钢的理论重量,kg;R为钢材效率系数。
从图3 能够得到,支撑结构随着高跨比的增大,承载力能力大幅度增大,材料系数R也随之增大,在高跨比1/5~1/3 范围,材料系数R达到峰值并有所下降,在高跨比1/9~1/6 范围,极限荷载与材料系数近似线性增加。考虑施工作业空间和经济性,兼顾支撑结构的极限承载力及材料效率,大跨度鱼腹梁设计时最优的高跨比应为1/9~1/6。

图3 鱼腹梁支撑高跨比与钢材效率系数及极限承载的关系Fig.3 The relationship between the height-span ratio of the fish-belly beam support and the steel efficiency coefficient and ultimate load-bearing capacity
3.2 腹杆的刚度对大跨度鱼腹梁支撑刚度的影响
鱼腹梁支撑腹杆承受轴力产生压弯变形,为研究腹杆自身的刚度对鱼腹梁支撑刚度的影响,通过采用MIDAS/GTS NX 有限元软件进行建模分析,得到腹杆刚度对大跨度鱼腹梁挠度结果的影响如表1 所示。

表1 腹杆刚度对大跨度鱼腹梁挠度结果的影响Table 1 Influence of web member stiffness on deflection results of long-span fish-belly beam
可以看出由H350 至H428 腹杆刚度增加近1.1 倍,鱼腹梁跨中挠度降低约92%,当采用H428 型腹杆产生的鱼腹梁跨中挠度近似于腹杆等效为抗压刚度无限大的桁架构件,表明腹杆刚度强弱很大程度上决定自身压弯变形进而显著影响鱼腹梁跨中挠度。
3.3 弦索的拉力对大跨度鱼腹梁支撑刚度的影响
采用MIDAS/GTS NX 有限元软件输入预加荷载的方式对鱼腹梁钢绞线施加预应力,得到鱼腹梁支撑系统的挠度变形,相比传统的分析方法更为简便、准确。
算例:鱼腹梁钢绞线数量采用40 根,分别对鱼腹梁钢绞线施加6 200 kN、6 400 kN、6 600 kN、6 800 kN 和7 000 kN 的预应力,得到施加预应力后的鱼腹梁挠度变形如表2 所示。经过理论计算与软件模拟分析等到鱼腹梁支撑结构跨中挠度、抗弯刚度和等效刚度,简化条件后的理论计算与软件模拟分析的结果非常接近,表明本文施加预应力后的鱼腹梁结构等效平均刚度计算公式精度相对较高。

表2 施加弦索拉力的大跨度鱼腹梁的变形与刚度Table 2 Deformation and stiffness of long-span fish-belly beam with string tension
3.4 上弦梁的刚度对大跨度鱼腹梁支撑刚度的影响
在均布荷载150 kN 条件下,分别建立不同上弦梁刚度的鱼腹梁模型,得到分析结果见图4。

图4 上弦梁刚度对鱼腹梁支撑跨中挠度影响Fig.4 Influence of upper chord beam stiffness on midspan deflection of fish-belly beam support
从图中可看出,鱼腹梁上弦梁刚度对支撑系统的等效刚度影响较为明显,上弦梁采用H400双拼、H400 三拼、H428 单拼和H428 双拼发挥出刚度效用,相比其他组合方式能够有效地控制鱼腹梁支撑的跨中挠度。
3.5 支座的刚度对大跨度鱼腹梁支撑刚度的影响
鱼腹梁支撑结构两端采用三角件与上弦梁、角撑相连接,鱼腹梁轴向位移在一定程度上受到限制,支座的实际情况更符合两端不动铰支座,采用MIDAS/GTS NX 有限元软件分别建立简支支座和不动铰支座两种条件下的鱼腹梁模型,由计算结果可知简支支座下的鱼腹梁跨中挠度比不动铰支座条件下高约10%,两者挠度基本相等,可以不考虑支座类型对鱼腹梁跨中挠度计算结果的影响。
4 控制基坑变形大跨度鱼腹梁设计方法
4.1 预应力刚度的定义
施加预应力后的等效刚度得到鱼腹梁平均等效刚度[10]为:

4.2 基于刚度控制的鱼腹梁形状参数优化设计
结合上述理论推导分析计算与有限元软件模拟分析,采用刚度控制方法对鱼腹梁形状参数进行优化设计,如表3 所示。

表3 鱼腹梁支撑刚度控制方法Table 3 Control method for stiffness of fish-belly beam support
4.3 基于变形量控制的鱼腹梁跨度设计方法
鱼腹梁支撑因其自身结构的特殊性,针对大跨度鱼腹梁设计除了考虑刚度控制外,还应重点关注位移控制条件下鱼腹梁跨度设计参数的选取,如表4 所示。

表4 鱼腹梁支撑位移控制方法Table 4 Control method for displacement of fish-belly beam support
4.4 设计计算方法的验证结果
本工程为澳门新城的深基坑,其平面近似为正方形,基坑周长约396 m,边长约99 m,深度为15.4 m。基坑采用钢板桩+预应力鱼腹梁钢支撑系统支护形式,分别在±0.00 以下-0.8 m、-4.5 m、-8.2 m 和-10.8 m 处设置4 道预应力鱼腹梁钢支撑系统,鱼腹梁跨度为38 m,开挖效果如图5 所示,钢支撑的平面布置如图6 所示。

图5 基坑大跨度鱼腹式钢支撑支护布置图Fig.5 Layout of large-span fish-bellied steel support for foundation pit

图6 基坑大跨度鱼腹式钢支撑平面布置图Fig.6 Layout plan of large-span fish-bellied steel support for foundation pit
采用MIDAS/GTS NX 有限元分析软件对基坑进行整体位移计算分析,设计参数见表5,选择其中一个典型剖面的土体深层水平位移结果进行对比,实测数据结果与软件模拟结果如图7 所示。

表5 大跨度鱼腹梁支撑设计参数Table 5 Design parameters of long-span fish-belly beam support

图7 基坑土体深层水平位移实测与模拟结果Fig.7 Measured and simulated results of deep horizontal displacement of soil in foundation pit
可以看出,实测数据与有限元模拟数据变化趋势大体一致,受土方开挖的时间效应、降雨渗流问题、基坑周边堆载、温度效应以及土体参数选取与实际土体存在偏差等多种因素的影响,导致基坑部分实测数据与有限元模拟数据存在一定偏差。结果对比表明,理论与模拟计算的刚度存在一定程度上的偏差,对于基坑工程安全而言属于可控状态,因此,采用有限元分析方法能够较为准确模拟基坑工程变形发展规律,为工程实践提供参考。
选取基坑中具有代表性的第2 道和第3 道鱼腹梁支撑,结合有限元分析计算可求出鱼腹梁平均等效刚度。理论推导与有限元模拟分析得出的刚度结果如表6 所示。
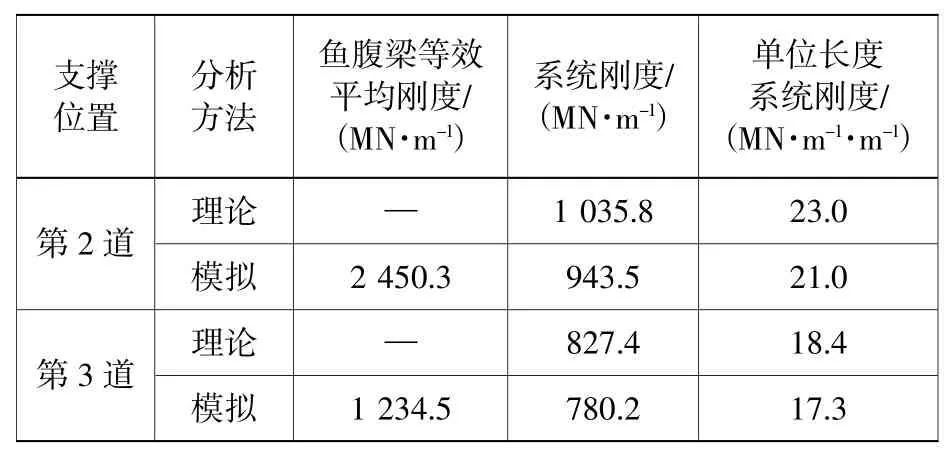
表6 理论与模拟计算刚度结果对比Table 6 Comparison of theoretical and simulated stiffness results
计算结果对比表明,理论与模拟计算的刚度存在一定程度的偏差,其原因是基于深基坑变形控制对大跨度鱼腹梁的高跨比、腹杆类型、弦索拉力、上弦梁刚度以及支座类型做了简化与优化设计,此外土体自身具有复杂性,选取相同土体基本参数应用于不同软件进行分析计算同样存在一定范围内的差异性,但两者计算方法得到的大跨度鱼腹梁支撑系统的刚度基本吻合,表明本文鱼腹梁支撑经参数优化计算得到的理论刚度较为准确,对大跨度鱼腹梁设计安全应用及节约成本具有指导意义。
5 结语
本文基于深基坑变形控制,从理论分析对大跨度预应力鱼腹式钢支撑系统的刚度进行深入研究分析,提出一些合理的计算方法,同时本文的研究也有一定的局限性,在鱼腹梁与竖向围护结构之间的连接方式及围护桩自身刚度对深基坑变形控制的影响需要作进一步的分析,以便进一步完善大跨度鱼腹梁支护的设计方法。通过本文研究主要得出以下结论:
1)考虑施工作业空间和经济性,兼顾支撑结构的极限承载力及材料效率,大跨度鱼腹梁设计时最优的高跨比范围为1/9~1/6。
2)鱼腹梁支撑腹杆承受轴力产生压弯变形,腹杆刚度强弱很大程度上决定自身压弯变形进而显著影响鱼腹梁跨中挠度,工程设计中应充分考虑腹杆刚度问题。
3)预加力能够改善鱼腹梁支撑的受力情况,提高装配式预应力鱼腹式钢支撑系统的表观刚度,同时还能弥补对角撑松弛问题,对控制基坑的变形十分有利。
4)鱼腹梁上弦梁刚度对支撑系统的等效刚度影响较为明显,上弦梁采用H400 双拼、H400 三拼、H428 单拼和H428 双拼发挥出刚度效用,能够有效地控制鱼腹梁支撑的跨中挠度。
