架空梁式圆管横向结构内力计算的弹性理论解析法

蔡勇斌，蔡勇平，蔡晓鸿

（1.吉安市水利局，江西吉安，343000；2.吉安市水利水电规划设计院，江西吉安，343000）

0 引言

输水管道有时需跨越河谷溪沟，但又不便深埋，往往采用架空跨越更为合理，其结构型式类似于横断面为圆形的封闭式渡槽。此时，作用于管桥中间段单位管长脱离体上的荷载除管体自重、均匀内水压力、水重外，管段两截面之间还存在剪力差，剪力差与上述荷载之和维持平衡。其内力计算，以往均视圆管横断面为在荷载和反力作用下处于平衡状态的三次超静定环形结构，采用结构力学的弹性中心法列出力法方程，求解出其超静定结构多余力，再据圆管截面的静力平衡方程进行内力求算。为此，采用了如下简化处理措施[1]：一是利用结构的对称性，假想从管顶切开，然后用钢臂将切口点与弹性中心点（可证明圆管的弹性中心即为圆心）相连接；二是将切口处的未知力移至弹性中心，列出其力法方程式，求算出未知力，再据静力平衡方程求得圆管任一断面的内力。

利用钢臂进行简化处理，其本质是假定在荷载作用下，圆管顶点无任何相对位移，而这与弹性理论揭示的圆管内力精确解及管顶部位的变形性态不协调一致，且未能反映圆管材料抗力参数对内力及变形的影响。因此，有必要采用弹性力学圆弧曲梁计算模型，建立自重、均匀内水压力和满管水重荷载并计及与荷载竖向作用相平衡的截面剪力作用下的弹性圆弧曲梁控制微分方程，推求架空梁式圆形管道横向结构内力与变位的弹性理论精确解析计算式。

1 弹性圆弧曲梁控制微分方程

图1（a）为满管水重、均匀内水压力荷载及圆管截面剪应力τ分布示意图，图1（b）为管体自重、均匀内水压力、满管水重、剪力引起的圆弧曲梁内力计算简图。

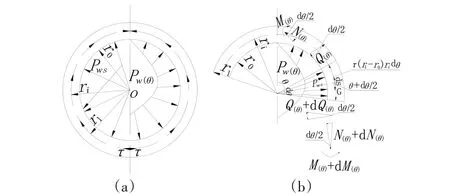
图1 自重、均匀内水压力、满管水重与环间截面剪力引起的内力计算简图Fig.1 Calculation of internal force under the effect of dead weight,uniform internal water pressure,full tube water load and shearing force

圆管横向内力计算时，沿槽长方向取单位管长按平面问题进行分析，作用于单位管长脱离体向下的管体自重、均匀内水压力、满管水重等荷载与脱离体两侧横截面上的剪力差维持平衡。设τ为分布于圆管截面上的剪应力，则τ(r1-r0)为管体壁厚切线方向的剪力，沿圆管壁厚中心线的切线方向向上作用。圆心角为θ断面的弯矩为M(θ)、剪力为Q(θ)、轴力为N(θ)。上述各力与圆心角θ的正负号约定均以图示方向为正。显见，图中满管水重荷载为：

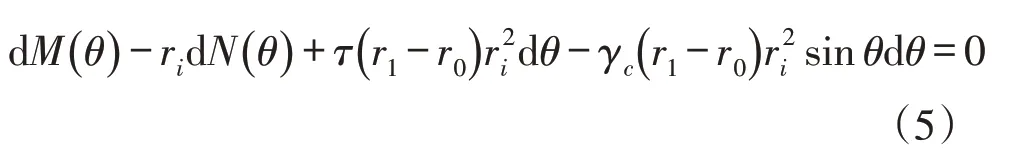
将式（2）代入式（4）和式（5）分别得式（6）和式（7）：

式（6）和式（7）表明，微元段截面上的剪力τ(r1-r0)对切线方向的内力、对原点O的力矩，与架空圆管自重荷载产生的切线方向的内力及对原点O的力矩方向相反，起抵消作用。因此，计及截面剪力作用的架空圆管管壁厚度可以减薄，即圆管截面上的剪力具减载效应。

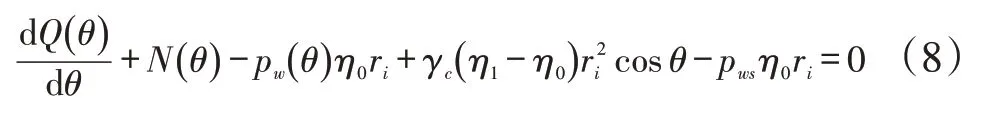
对式（7）从0到θ积分，整理得：

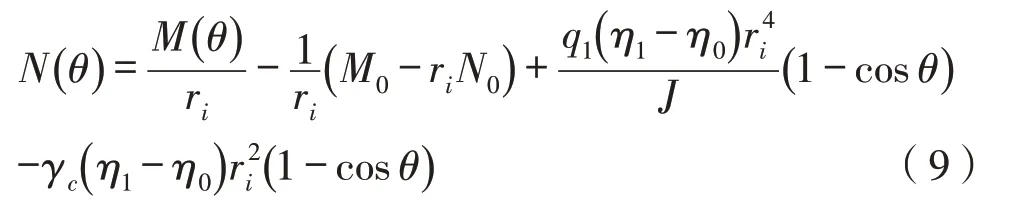
式中：γw为水的重度。

剪应力τ的计算式为：

式中：q1为单位管长圆管自重与满管水重，即；γc为圆管材料重度；J

据式（6）和式（7）可得：为圆管惯性矩（应注意辨识圆管环截面对中性轴的惯性矩J与单位管长管壁对其中性轴之惯性矩I的差异）。

如图1（b）所示，架空圆管弧段可视作弹性圆弧曲梁。设圆心为坐标原点，截取微分单元r idθ，起始断面的弯矩为M(θ)、剪力为Q(θ)、轴力为N(θ)，列出微段的静力平衡方程∑F r=0（沿微段径向的力平衡方程）、∑Fθ=0（沿微段切线方向的力平衡方程）、∑M o=0（对原点O的力矩方程），略去二阶微量后有：

将式（8）和式（9）代入式（10），整理后有：

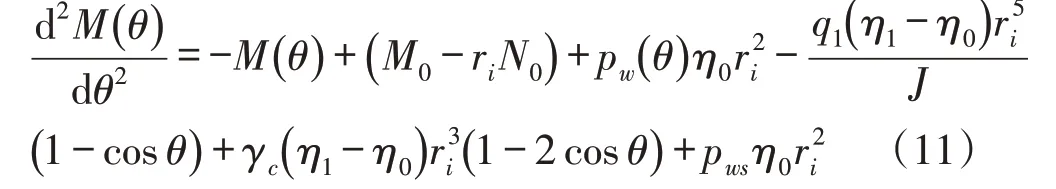
对式（6）求导，并将式（1）和式（8）代入，化简后有：

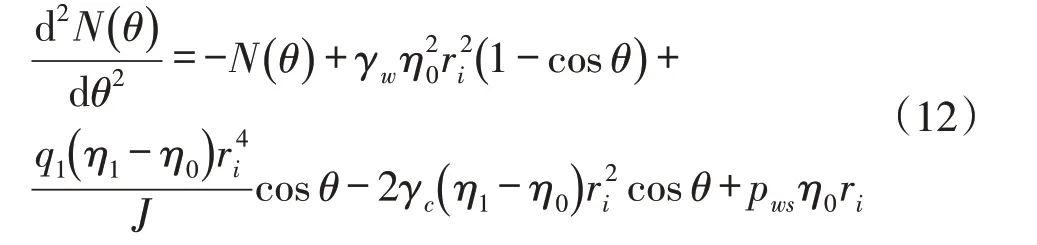
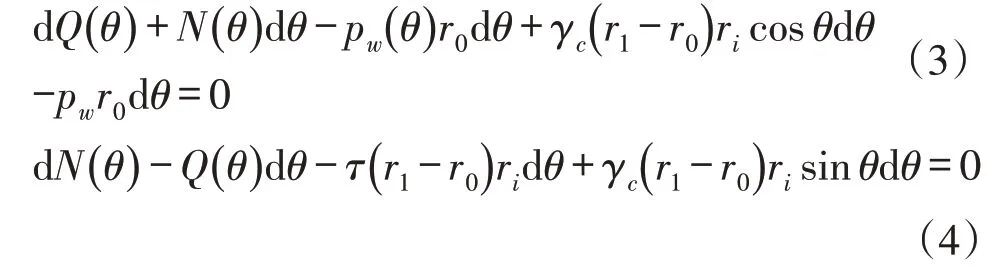
设架空圆管材料的弹性模量为E c，圆管计算截面的径向位移为w(θ)，断面面积为F，管壁对其中性轴的惯性矩为I，则据结构力学知，截面的径向位移w(θ)与截面内力间有关系式：

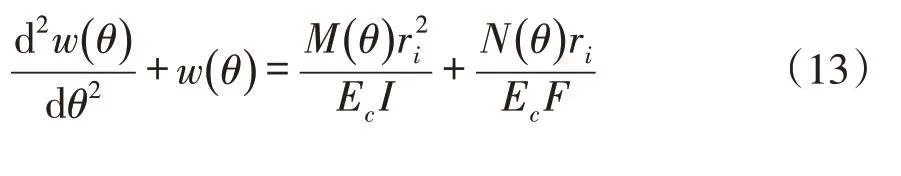
对式（13）求导2次，并将式（11）和式（12）代入，可得径向位移w(θ)应满足的控制微分方程：

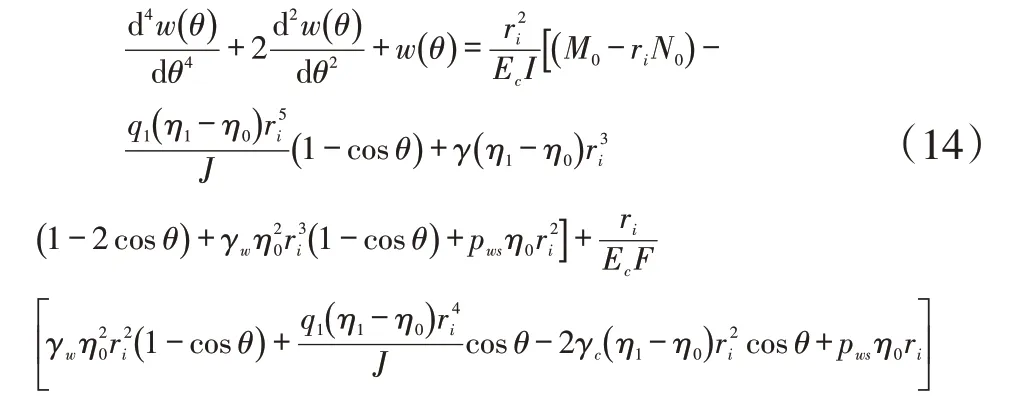
式（14）即为受架空圆管自重、均匀内水压力和满管水重并计及截面剪力作用下的弹性圆弧曲梁控制微分方程。

2 弹性圆弧曲梁内力与变位计算

微分方程式（14）的通解由特解w0(θ)与基本解w

1(θ)组成，即：

特解w0(θ)可利用微分算子法求得[2]。据微分方程理论有算子多项式：

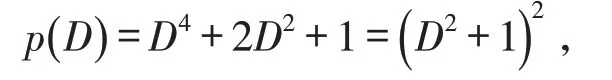
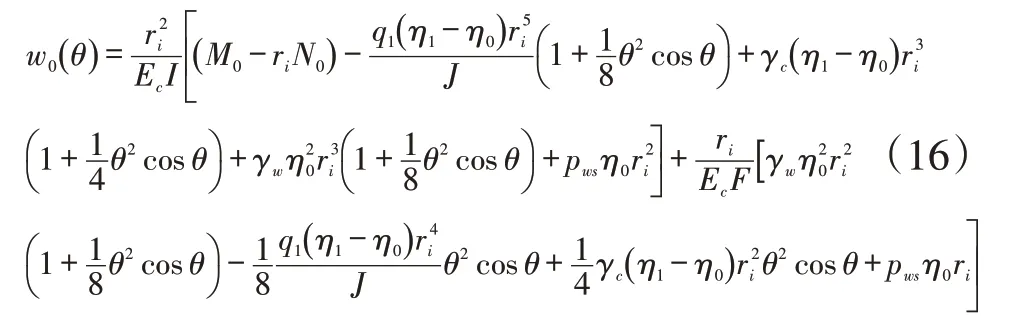
基本解w1(θ)可由下列特征方程确定[2]：

式（17）有二重根λ1与λ2：

在学习目标阐述环节，教师要避免的误区是将“学习目标”设定为“教学目标”，应从学习者的角度对学习者应达到的目标进行行为或者认知方面的阐述。良好的学习内容分析结果为学习目标提供了坚实的基础，继而是在分析学习目标完成后，依据一定的学习目标分类理论，结合具体的教学实际确定哪些层次的学习目标需在课前通过观看视频自主学习完成，哪些则是必须通过课堂上的活动才能够实现的。

于是控制微分方程式（14）的基本解为：

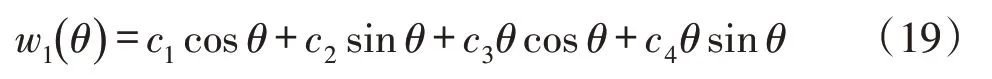
据对称性，w(-θ)=w(θ)对任意θ成立，可得c1=0、c2=0、c3=0、c4=0，从而得自重、均匀内水压力与满管水重作用下的架空圆管弹性圆弧曲梁控制微分方程的通解即为其特解，即有w(θ)=w0(θ)，对式（16）整理得：

忽略轴向力产生的切向应变εθ，于是由弹性理论及架空梁式圆管对称性有[3]：

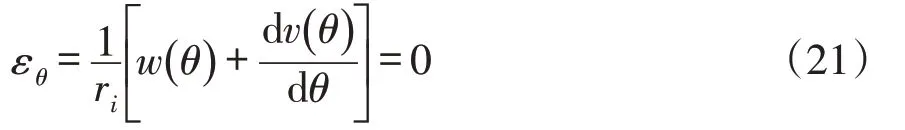
据式（21）得切向位移：

式中：c为积分常数。

将式（20）代入式（22），并利用V(θ)|θ=0=0确定积分常数c=0，可得：

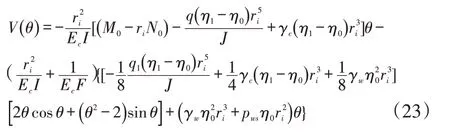
3 内力与变位计算

据式（9）有：

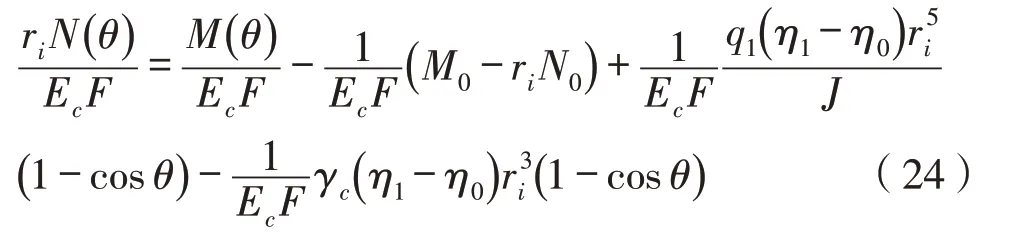
将式（24）代入式（13），整理得：

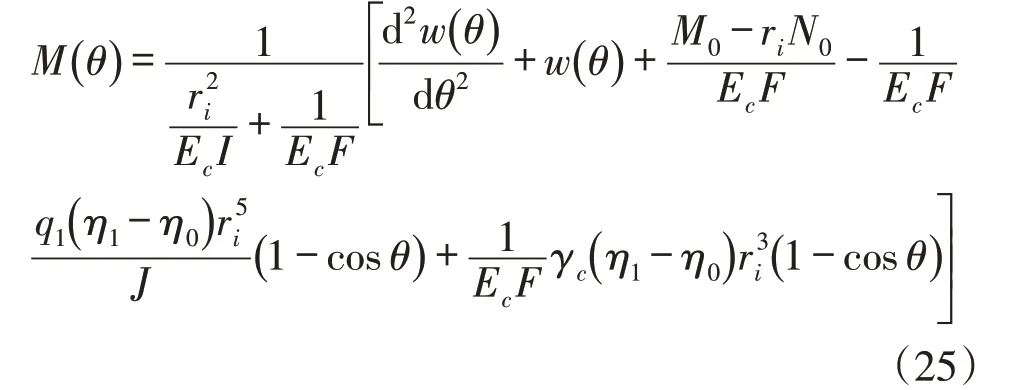
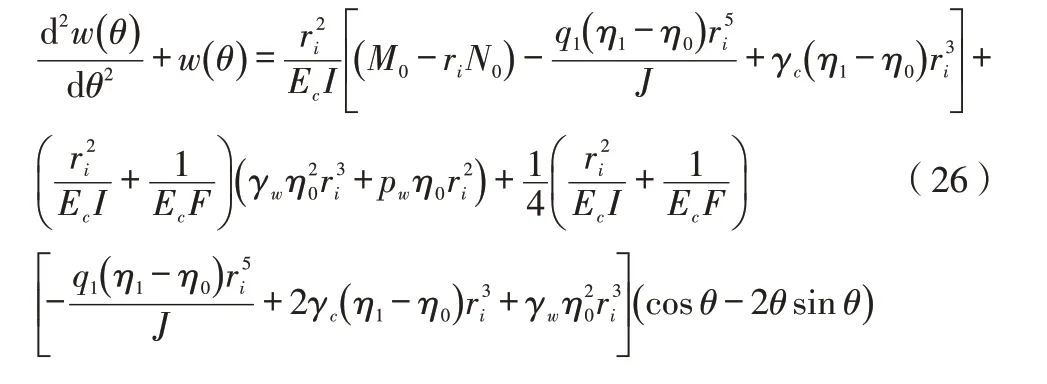
将式（26）代入式（25），化简得：

于是由式（9）可得轴力N(θ)计算式：

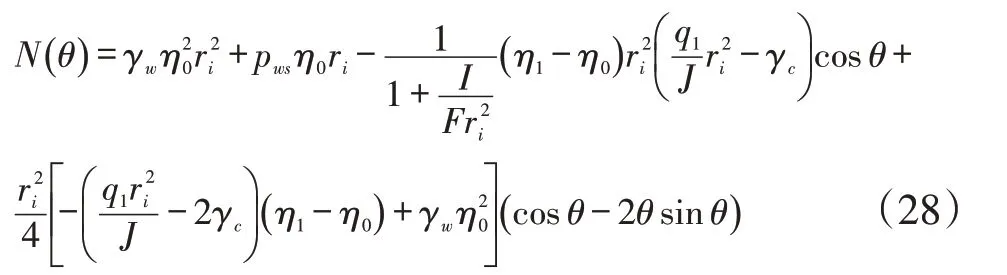
由自重、均匀内水压力和满管水重作用下的架空圆管切向应变对称性[4]，有：

将式（23）代入式（29），可求得：

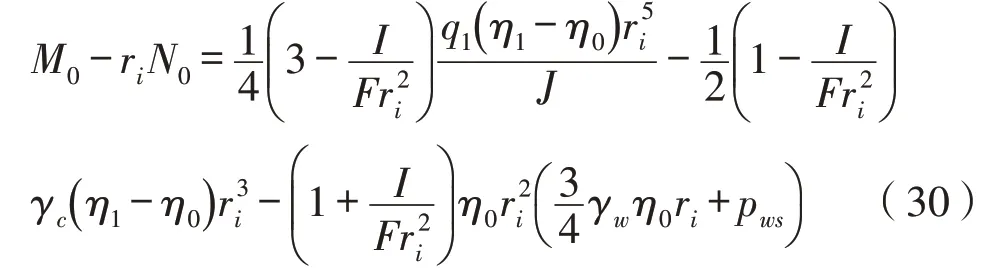
据式（28）可得：

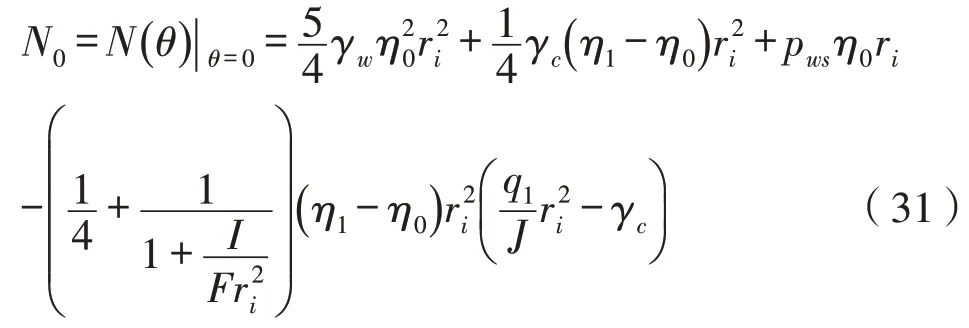
将式（31）代入式（30）得：

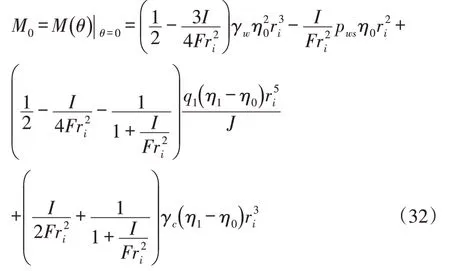
将式（30）代入式（27），得弯矩M(θ)计算式：

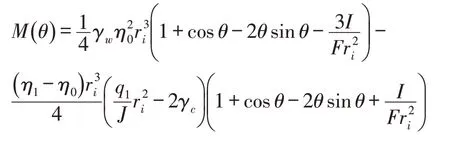
将式（31）、（32）分别代入式（20）、（23），则易得自重、均匀内水压力和满管水重作用下的架空圆管各计算截面径向位移w(θ)、切向位移V(θ)计算式，不予赘列。

式（28）和式（33）表明，自重、均匀内水压力和满管水重及计及截面剪力作用下的架空圆管计算截面弯矩M(θ)、N(θ)，除与圆管几何参数内半径r0、外半径r1及计算截面与竖向直径间的夹角θ有关外，还与架空圆管结构材料的物理力学参数弹性模量E c、计算截面的断面面积F、环截面对中性轴的惯性矩J及管壁对其中性轴的惯性矩I有关。有必要指出，现有架空圆管自重、均匀内水压力、满管水重及计及截面剪力作用所产生的弯矩计算式[1]，未全面揭示计算截面面积F（或抗拉/压刚度E c F）、环截面惯性矩J及管壁截面惯性矩I（或抗弯刚度E c I）对弯矩M(θ)、轴力N(θ)的影响，存有缺陷。

4 算例

引用参考文献[1]中的算例（书中例5-2），比较分析所推求弹性理论精确解计算结果与其存在的差异。

某简支架空梁式C25钢筋混凝土圆管内径D0=2.5 m，外径D1=3.1 m，管壁厚δ=0.3 m，压力水头H=18 m。计算圆管控制断面θ为0°、90°和180°的内力。

取单位长b=1.0 m架空钢筋混凝土圆管进行计算分析。钢筋混凝土圆管弹性模量E=2.55×107kPa，钢筋混凝土重度γc=25 kN m3；水的重度γw=10 kN m3；均匀内水压力p ws=180 kN m2。

单位长圆管管壁的截面积F=0.3 m2，圆管管壁对其中性轴的惯性矩，圆管环截面对其中性轴的惯性矩。

据式（28）和式（33），计算得架空梁式钢筋混凝土圆管控制断面θ为0°、90°和180°的轴力与弯矩如表1所示。

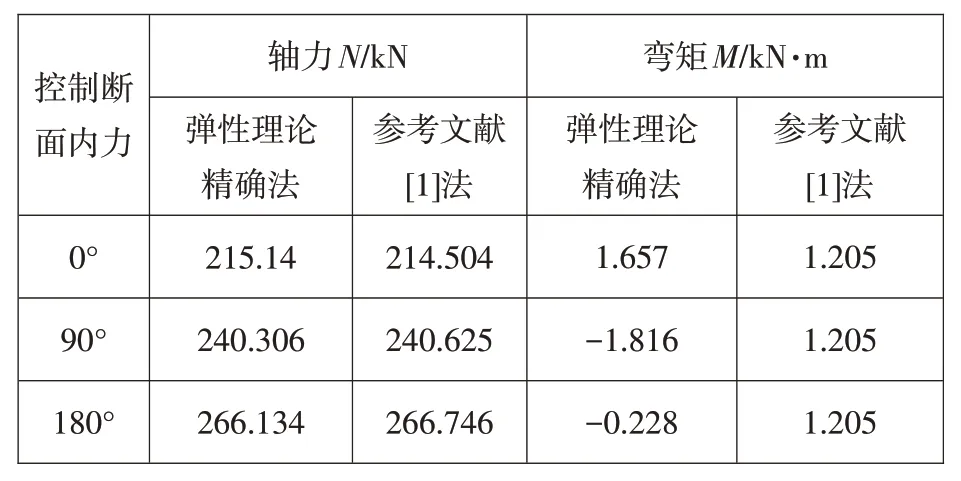
表1 架空梁式钢筋混凝土圆管内力计算结果Table 1 Results of calculation of internal force of aerial beamsupported reinforced circular pipe

比较表1中两种计算法的内力结果可见，各计算控制断面的轴力非常接近，而弯矩值则差异明显，参考文献[1]采用结构力学法计算得各控制断面的弯矩值相等，显然不合理。

5 结语

架空梁式圆管是常见输水建筑物之一，其横向结构内力通常采用结构力学弹性中心法所推求的近似计算公式求算，未全面揭示计算截面抗拉刚度、抗弯刚度及环截面惯性矩对弯矩、轴力的影响，计算结果往往未能反映结构的实际内力状况。文中推求的架空梁式圆管弹性理论精确解析法全面揭示了结构材料的相关物理力学参数、结构尺寸对其内力的影响，且计算过程简捷。