DFIG短路热效应对故障参数灵敏度的解析表达
2022-08-04李生虎张亚海
李生虎, 张亚海
(1.合肥工业大学 电气与自动化工程学院,安徽 合肥 230009; 2.新能源利用与节能安徽省重点实验室,安徽 合肥 230009)
0 引 言
近年来双馈感应发电机(doubly-fed induction generator,DFIG)等风电机组数量快速增加[1-2],有必要分析校验DFIG的安全稳定性,以维护电网安全。DFIG定子外侧三相短路时,短路电流最大,对绕组影响最严重。通过投入撬棒(crowbar)[3]、改变变流器或桨距角控制策略[4-5],可以减小短路电流。但是如果短路持续时间较长,那么热效应引起的温升仍可损坏DFIG及其相邻开关设备[6]。
与同步发电机相比,DFIG结构和控制方式不同[7-8],其转速不固定,而是由风速决定。等效转子电阻与转速和撬棒电阻有关。通过逐步积分方法,可以量化DFIG短路热效应、分析敏感因素,但是计算量较大,且不能区分热效应周期与非周期分量。因此最好能建立DFIG短路热效应和灵敏度的解析表达。
现有相关研究中,文献[9-10]分析了变流器损耗和热效应;文献[11]提出了一种DFIG多模式运行的控制策略,避免半导体过热;文献[12]建立了一种热阻抗模型,以分析半导体热损耗;文献[13]基于基频和负载变化,绘制了功率半导体年度热分布;文献[14]采用平均模型代替开关电路,仿真变换器热效应。上述热效应文献大都基于稳态情况,或是只针对个别电力电子器件,不适合分析DFIG热效应。引入故障后,文献[15]采用消磁电流控制防止转子电流幅度过大,从而降低热效应,但没有给出具体表达。基于DFIG短路电流解析表达,文献[16]推导了热效应解析表达,但没有区分热效应周期与非周期分量,也未判断敏感因素。
对DFIG热效应分析的难点在于:
(1) 逐步积分得到的短路电流及热效应往往仅考虑周期分量,忽略非周期电流分量将导致热效应结果的误差。
(2) 热效应各分量对不同参数的灵敏度差异较大;建立热效应完整表达对参数灵敏度的解析表达,不但形式复杂、计算成本增加,也缺乏工程必要性,需要合理简化。
影响DFIG短路电流及热效应的参数很多,如定转子电阻、定转子暂态时间常数、定转子暂态电感、撬棒电阻、定子电压降等。研究热效应对定子电压降比例灵敏度解析表达,可直接量化电压跌落程度对热效应的影响。考虑转子电压、电流等约束,撬棒阻值选择在一个区间内而非定值。研究热效应对撬棒阻值灵敏度的解析表达,可以在满足故障穿越和热稳定前提下,合理选择阻值。
本文对DFIG短路电流解析表达的平方求积分,建立热效应解析表达;通过分解热效应,提出周期与非周期分量的解析表达;分析各分量衰减特性和影响因素,建立热效应实用表达形式;提出热效应对定子电压降和撬棒电阻的灵敏度。所提模型有助于估计DFIG短路热效应,判断相关影响因素,为风电场热稳定检验提供计算工具。
1 DFIG短路热效应的解析表达
1.1 DFIG短路电流的解析表达
DFIG结构如图1所示[17-18],包括风力机、感应电机、转子侧变流器(rotor-side converter, RSC)、网侧变流器(gird side converter, GSC)和撬棒电阻Rcb等。Rcb与转子并联,正常工作时断开。当转子电流过大时,Rcb投入,形成旁路,减小短路电流[19-20]。相比撬棒电阻,晶闸管损耗较小,对电流和热效应影响不大,因此忽略。
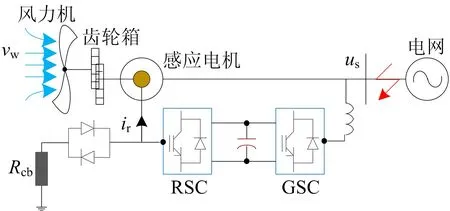
图1 DFIG结构
定子外侧三相短路时,短路电流很大,撬棒启动虽可减小短路电流,但若持续时间较长,发热较为严重。因此取t=0时的定子三相短路,撬棒启动后的DFIG等效电路如图2所示。其中:u、i、R和L分别为电压、电流、电阻和电感;Ls=Lsσ+Lm,Lr=Lrσ+Lm,Lsσ、Lrσ分别为定子漏感和转子漏感,Lm为激磁电感;下标s、r分别代表定子和转子。

图2 含撬棒的DFIG等值电路
定、转子电压和磁链方程为:
us=Rsis+pψs+jωψs,
ur=Rrir+pψr+jsωψr=0,
ψs=Lsis+Lmir,
ψr=Lmis+Lrir
(1)
其中:ψ为磁链;ω为同步角速度;s为转差;p为微分算子。
根据电压与磁链关系,推导电流与磁链关系,得DFIG短路电流解析表达式,其中转子磁链稳态分量ψrf∞影响不可忽略[21-22]。考虑到电弧电阻,ψrf∞不为0,表达式[16]为:
(2)
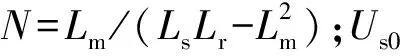
考虑转子磁链稳态分量,用派克变换将短路电流由dq坐标系转化为abc旋转坐标系,得a相短路电流为:
(3)
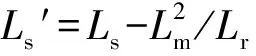
(4)
其中:is0为故障前定子电流;Zs=Rcb+jωLs′为定子侧等效阻抗。
1.2 DFIG短路热效应的解析表达
根据(3)式,采用逐步积分方法,将DFIG短路热效应展开为10个分量之和,得热效应解析表达[16]:
(5)
其中:tf为短路持续时间;Qτ为热效应分量,τ=1,2,…,10,其中Q3、Q4、Q6、Q7、Q8、Q9、Q10含有ψrf∞。显然,ψrf∞的影响不可忽略。
各分量衰减规律见表1所列。

表1 热效应分量衰减规律
表1中:周期分量Q1、Q3、Q6与时间成正比;非周期分量Q2、Q5、Q8按定子暂态时间常数缓慢衰减;Q4、Q7、Q10按转子暂态时间常数衰减,衰减较快;Q9按定转子并联结构暂态时间常数衰减,衰减最快。
因此,可以将(5)式改写为:
Q=Qp+Qap
(6)
(7)
其中:Qp为周期分量之和;Qap为非周期分量之和。
热效应各分量中,Q4、Q10不含定子电压降比例;非周期分量除Q2外,其余数值较小。折衷准确性和实用性,忽略分量Q4、Q5、Q7、Q8、Q9、Q10,建立针对定子电压降的热效应表达为:
Qa=|Q1+Q2+Q3-Q6|
(8)
转子磁链稳态分量、故障前转子磁链瞬时值、转子暂态时间常数均含有撬棒电阻,且表达为指数形式,对热效应分量稳态值影响较大。Q5不含撬棒电阻;Q10含平方项与乘积项,对撬棒电阻的灵敏度表达比较复杂;Q7具有向量特性,会引起热效应较大误差,且相比Q4、Q8、Q9,Q7数值较小。折衷准确性和实用性,选择Q1、Q2、Q3、Q4、Q6、Q8、Q9,建立针对撬棒电阻的热效应表达为:
Qb=|Q1+Q2+Q3+Q4-Q6-Q8-Q9|
(9)
以下分别将(8)式和(9)式记为热效应表达a和b。
2 热效应对参数灵敏度的解析表达
2.1 热效应灵敏度解析表达的检验
为验证后续灵敏度模型的准确性,采取摄动法求取灵敏度,表达式[23]为:
(10)
其中:μ为摄动值;ζ为短路参数。
2.2 热效应对定子电压降比例灵敏度解析表达
根据热效应表达a,代入热效应各分量的具体表达,可将 (8) 式改写为:
(11)
由于ψrf∞含有定子电压降比例,需将其展开,以求取Qa对定子电压降比例的偏导。根据 (2) 式和 (11)式,Q3、Q6可改写为:
(12)

(13)
结合 (12) 式、(13) 式,得热效应对定子电压降比例的灵敏度解析表达为:
SQa,G=SQ1,G+SQ2,G+SQ3,G-SQ6,G
(14)
其中:SQ1,G、SQ2,G、SQ3,G、SQ6,G分别为各热效应分量对定子电压降比例的灵敏度,具体表达式分别为:
(15)
显然,SQ1,G、SQ2,G、SQ3,G、SQ6,G与短路时间成正比,SQ2,G含有衰减分量,随短路持续时间的增加而逐渐衰减。
2.3 热效应对撬棒电阻灵敏度的解析表达
热效应表达b包含分量的具体表达为:
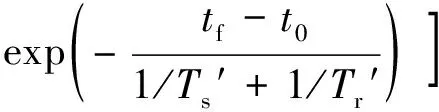
(16)
其中,A=ψr0-ψrf∞为故障前转子磁链瞬时值与转子磁链稳态值之差。Q1、Q2对Rcb灵敏度为0。
由于转子磁链稳态分量、故障瞬间转子磁链的瞬时值以及转子暂态时间常数含有撬棒电阻,先求其对撬棒电阻的灵敏度解析表达。
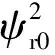
(17)

((jsωLr′+Rcb+Rr)-(Rcb+Rr)ω2)]=E4
(18)
Tr′对Rcb的灵敏度为:
(19)
结合E1~E5,对撬棒电阻求偏导,得到热效应对Rcb的灵敏度解析表达为:
SQb,cb=SQ1,cb+SQ2,cb+SQ3,cb+
SQ4,cb-SQ6,cb-SQ8,cb-SQ9,cb
(20)
其中,SQ1,cb、SQ2,cb、SQ3,cb、SQ4,cb、SQ6,cb、SQ8,cb、SQ9,cb分别为对应分量对Rcb的灵敏度,具体表达式分别为:
(21)
其中,η=2GkrUs0Ts′。显然,SQ3,cb、SQ6,cb与短路时间成正比,SQ4,cb、SQ8,cb、SQ9,cb含有衰减分量,随短路时间的增加而逐渐衰减。
以上灵敏度模型适用于不同运行场景和故障参数。例如:模仿故障严重程度,可改变定子电压降比例;模仿不同风速,可改变转差等。
3 算例分析
采用MATLAB编写程序,计算DFIG短路热效应对定子电压降比例和撬棒电阻的灵敏度及其误差和仿真时间,其中DFIG参数[16]见表2所列,c1~c9为风机的拟合系数。

表2 1.5 MW DFIG参数
取空气密度ρ=1.225 kg/m3,风速υw=8 m/s,Rcb=0.1 pu,Us0=1 pu,G=0.8 pu,μ=0.000 1 pu。按风电并网规程,出现故障后,当定子电压跌落至0.2 pu时,撬棒启动,引起电流周期分量变化。由于磁链不能突变,引入直流分量,两者叠加,电流衰减振荡,直至达到稳态。DFIG短路电流逐步积分、本文和文献[22]解析模型的仿真结果如图3所示。由图3可知,本文解析模型结果与逐步积分的误差更小。
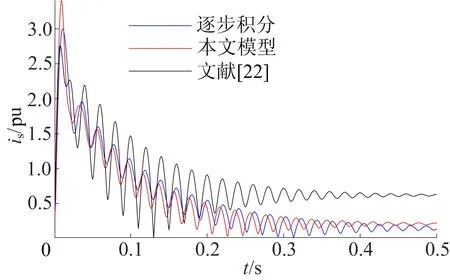
图3 DFIG短路电流
各分量随时间变化情况如图4所示。图4a所示为周期分量,与短路时间大致成正比,数值较大;图4b所示为非周期分量(含衰减分量),短路初期快速增加后趋于饱和,除Q2外数值较小。
DFIG短路电流热效应如图5所示。图5a所示为DFIG短路电流热效应的逐步积分、热效应表达a和b的仿真结果。相比b表达,a表达与逐步积分仿真结果更为接近,可用于求热效应对定子电压降比例的灵敏度。b表达中含Q4、Q8、Q9,使得非周期分量占比增大,在短路初期热效应迅速增加。由图5b可知,Q8、Q9具有向量特性,灵敏度为各分量之和,但|A+B|≠|A|+|B|,由此造成热效应误差。

图4 DFIG短路电流热效应分量特性

图5 DFIG短路热效应
3.1 热效应对定子电压降比例的灵敏度
热效应对定子电压降比例灵敏度的解析表达与逐步积分摄动仿真结果如图6所示。在短路初期,SQ2,G迅速增加,导致热效应对定子电压降比例的灵敏度快速增加,在0.15 s时达到最大值。随着短路持续时间增加,SQ2,G衰减加快和SQ6,G增大,灵敏度减小。在故障后约0.15 s以内,2种方法得到的灵敏度较为吻合。在后续时间内,两者变化趋势基本一致,证实了所提灵敏度解析表达的准确性。
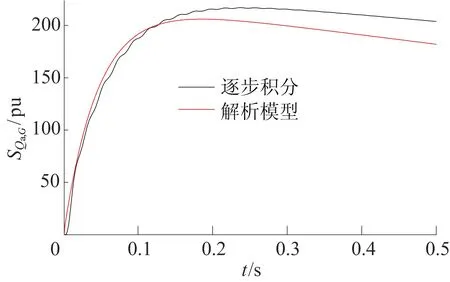
图6 热效应对定子电压降比例灵敏度
不同时刻2种灵敏度模型的误差见表3所列。相较于逐步积分摄动法,解析模型最大误差为8.1%;考虑到散热和温升计算精度一般不高,所提灵敏度解析表达误差大致可以接受。2种方法仿真时间的比较见表4所列。逐步积分摄动法所需时间约是解析表达的2.3倍,验证了所提灵敏度解析表达的应用价值。

表3 热效应对定子电压降比例灵敏度的误差

表4 热效应对定子电压降比例灵敏度的仿真时间
3.2 热效应对撬棒电阻的灵敏度
热效应对撬棒电阻灵敏度的解析表达与逐步积分摄动仿真结果如图7所示。由于SQ4,cb、SQ8,cb、SQ9,cb在短路初期快速增加,热效应对撬棒电阻的灵敏度在短时间内达到最大值。随着短路持续时间增加,SQ4,cb、SQ8,cb、SQ9,cb衰减加快,SQ3,cb、SQ6,cb数值增大,灵敏度先减小后增大。在故障后约0.1 s以内,2种方法得到的灵敏度较为一致。在后续时间内两者变化趋势基本一致,证实了所提灵敏度解析表达的准确性。
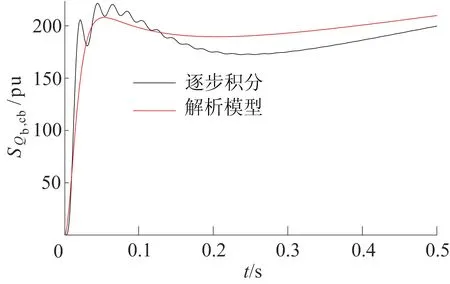
图7 热效应对撬棒电阻灵敏度
不同时刻2种灵敏度模型的误差见表5所列。相较于逐步积分摄动法,解析模型最大误差为10.4%。2种方法的仿真时间的比较见表6所列。逐步积分摄动法所需时间约是解析表达的3倍,验证了所提灵敏度解析表达的应用价值。
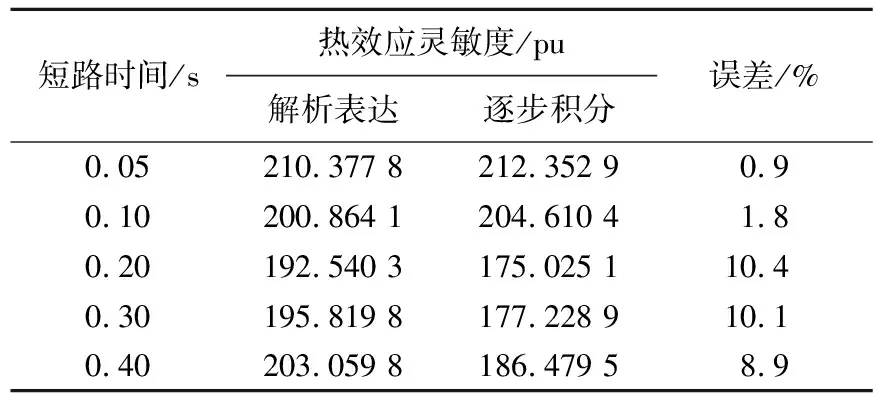
表5 热效应对撬棒电阻灵敏度的误差

表6 热效应对撬棒电阻灵敏度仿真时间
4 结 论
本文提出双馈风电机组短路热效应周期分量与非周期分量的解析表达;根据各分量衰减特性及其影响参数,综合考虑准确性和实用性,建立热效应实用解析表达;为准确量化短路参数对热效应影响并降低计算成本,推导出热效应对故障参数灵敏度的解析表达。
仿真结果表明:在故障初期,热效应非周期分量较为明显,因此不可忽略;定子电压降直接影响热效应各分量,对热效应的影响较大;撬棒电阻影响转子磁链的瞬时值、转子磁链稳态分量和转子暂态时间常数,进而影响热效应各分量,对热效应的影响较大。
