“一线三直角”模型的构建与应用*
2022-08-04215151苏州市阳山实验初级中学校赵小花
中学数学 2022年5期
215151 苏州市阳山实验初级中学校 赵小花
在初三数学的复习过程中,学生经常会碰到二次函数与几何相关联的探究题,因题型多样,综合性强,学生往往无从下手.
如果教师在讲解过程中只是就题论题,学生对题目的认识可能只是浮于表面,是碎片化的.
要想加深学生对问题的理解和把握,需要帮助学生建立完整的知识结构,挖掘问题的内涵和外延,抓住本质,才能达到“知一法,通一类”的效果.
笔者近期开设了一节二次函数的专题复习课,通过对大量习题的分类与研究,确定以构建“一线三直角”模型为本节课的主线,引导学生解决二次函数的一类综合题.
整节课衔接自然、流畅,题目设计精巧、有梯度,注重渗透数学思想,培养学生利用数学模型解决问题的能力,优化解题思路,达到了预期的复习效果.
1 教学目标
(1)掌握“一线三直角”模型的特点,能抓住本质特征,根据问题条件构造模型,归类并总结解题方法.
(2)经历发现问题、提出问题、分析问题和解决问题的过程,渗透数形结合、分类讨论、方程及模型思想,提升学生数学学习素养.
2 教学过程
2.1 问题引入,激趣唤知
问题1
如图1,在平面直角坐标系中,OB
⊥OA
,且OB
=2OA
,已知点A
(-1,2),求经过点A
,O
,B
的抛物线的解析式.
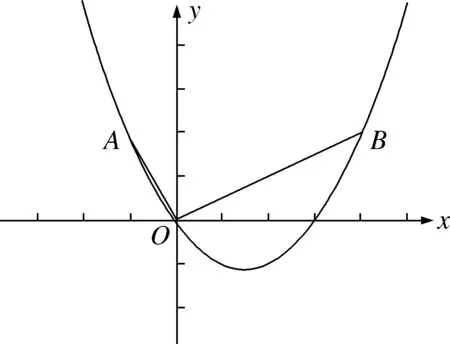
图1
师:求该抛物线解析式的关键是什么?
生1:确定点B
的坐标.
师:如何确定点B
的坐标?生2:构造“一线三直角”模型,利用相似.
师:能具体说说吗?
生3:如图2,过点A
作AM
⊥x
轴于M
,过点B
作BN
⊥x
轴于N.
因为OB
⊥OA
,则∠AMO
=∠BNO
=∠AOB
=90°,所以∠OAM
+∠AOM
=∠BON
+∠AOM
=90°,所以∠OAM
=∠BON
,得△AMO
∽△ONB
,所以因为A
(-1,2),所以AM
=2,MO
=1,所以ON
=4,BN
=2.
所以B
(4,2).
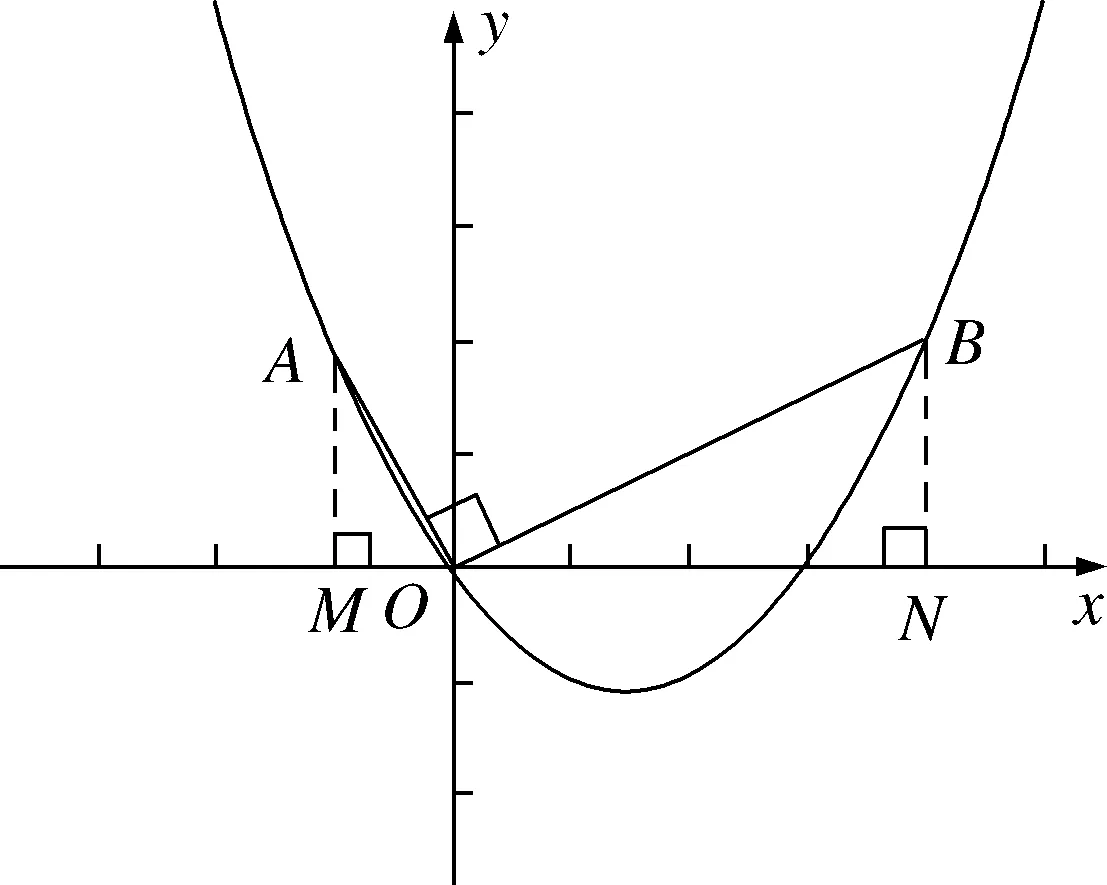
图2
师:很好,请同学们求出该抛物线的解析式.
众生:
设计意图:
本节课是关于二次函数背景下的“一线三直角”模型的应用,通过求抛物线解析式的问题引入,给学生的思维进行热身,既可以唤醒已有的知识经验,又能激发他们继续探索的兴趣.
求点B
的坐标引出了“一线三直角”模型,也为接下来模型的提炼做铺垫.
2.2 分析特征,提炼模型
师:刚刚求点B
坐标时,同学们构造了“一线三直角”模型,这个模型有什么特征?请同学们说一说,画一画.
生4:如图3,已知OA
⊥OB
,直线l
经过直角∠AOB
的顶点O
,分别过点A
,B
向直线l
作垂线段AM
,BN
,垂足记为点M
,N
,像这样,一条直线上有三个直角就构成了“一线三直角”模型.
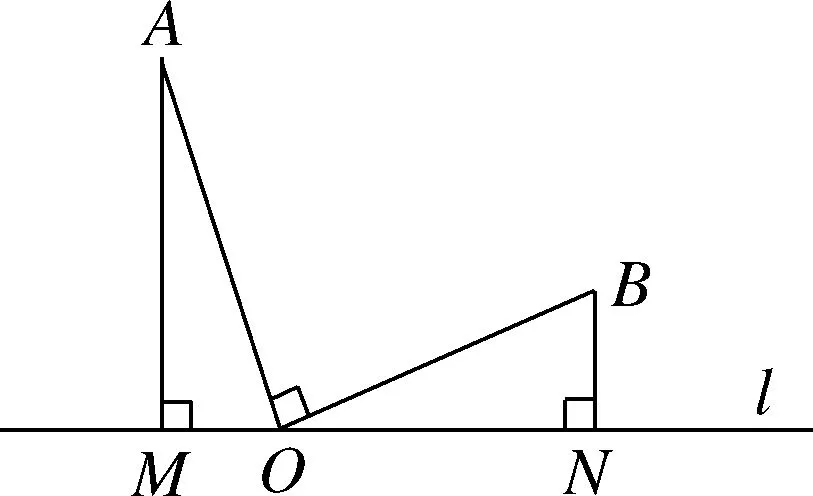
图3
师:根据模型可以得到什么结论?
生5:与问题1证明方法一样,可以证得△AMO
∽△ONB
,所以师:其他条件不变,将直线l
绕点O
旋转,结论还成立吗?如图4,若直线l
旋转至∠AOB
内部,结论还成立吗?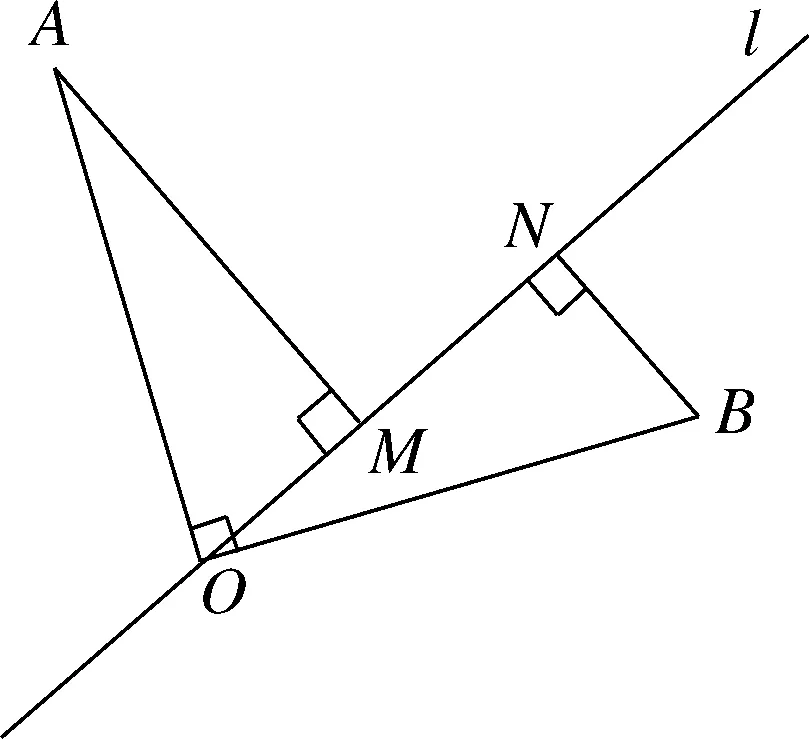
图4
生6:证明方法是一样的,仍然能够证得△AMO
∽△ONB
,所以结论成立.
师:图3和图4可以分别称为同侧型和异侧型的“一线三直角”模型.
若将模型一般化,把三个直角改为三个相等的角,变成“一线三等角”模型,结论有什么变化?生7:结论不变,△AMO
∽△ONB.
师:若将模型特殊化,添加条件OA
=OB
,有什么新发现?生8:相似三角形中一组等角的对边相等时,可以得到全等,所以此时△AMO
≌△ONB.
师:本节课主要研究“一线三直角”模型的构建和应用,其他内容暂不深入讨论.
做题时可以发现很多题目中的“一线三直角”模型并不会被直观、完整地呈现出来,需要自主构建,有什么方法?生9:可以分三步.
第一步,找到或挖掘题目中的直角;第二步,确定经过直角顶点的直线;第三步,向直线作垂线段.
总结为“找直角、定直线、搭框架”.
师:非常好.
接下来看看“一线三直角”模型还能够解决哪些二次函数的相关问题.
设计意图:
学习了全等和相似三角形后,学生对“一线三直角”模型已经有了一定的认识,但结合二次函数综合应用时往往需要自主构建模型,对学生的建模意识和能力也提出了更高的要求.
本环节通过学生的自主展示、复习和总结,既帮助基础薄弱的学生熟悉模型的特征和结论,为综合应用做铺垫,也有利于学生建立完整、系统的知识结构.
2.3 模型应用,总结方法
问题2
如图5,已知抛物线点A
(-1,2)在该抛物线上,能否在抛物线上找到一点B
,使得OB
⊥OA
?若能,求出点B
的坐标;若不能,请说明理由.
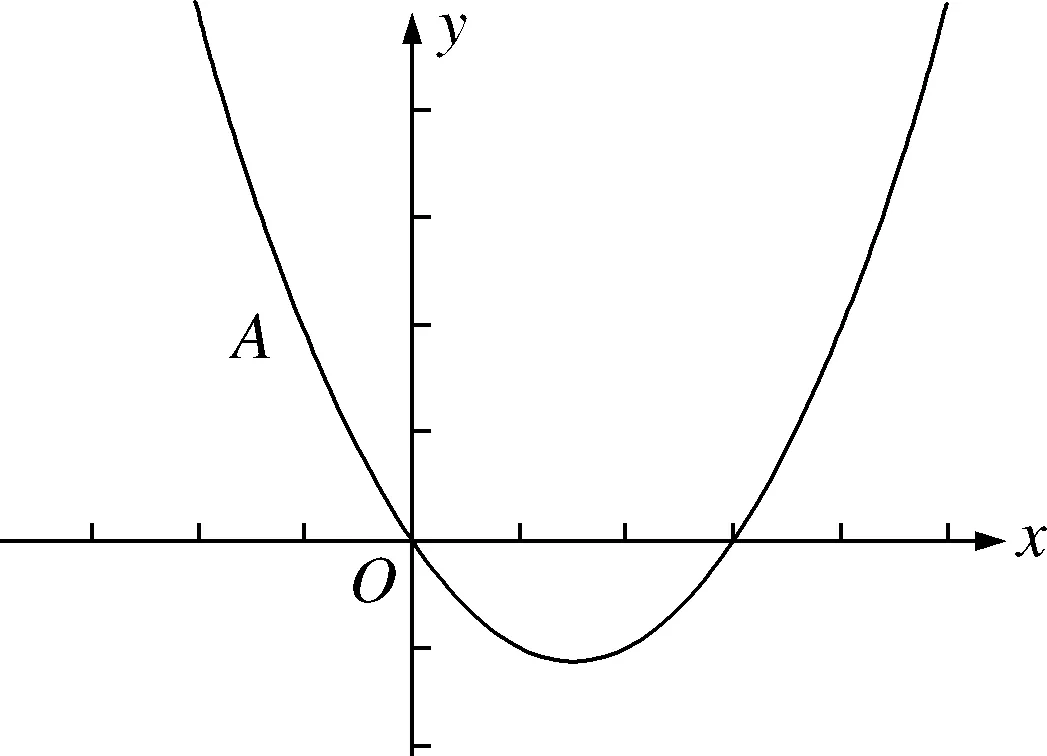
图5
师:读完题目大家有什么思路?
生10:要先确定点B
的位置,如图6,根据OB
⊥OA
,过点O
作OA
的垂线,与抛物线的交点即为点B.
再分别过点A
,B
作AM
⊥x
轴于M
,BN
⊥x
轴于N
,构造“一线三直角”模型.
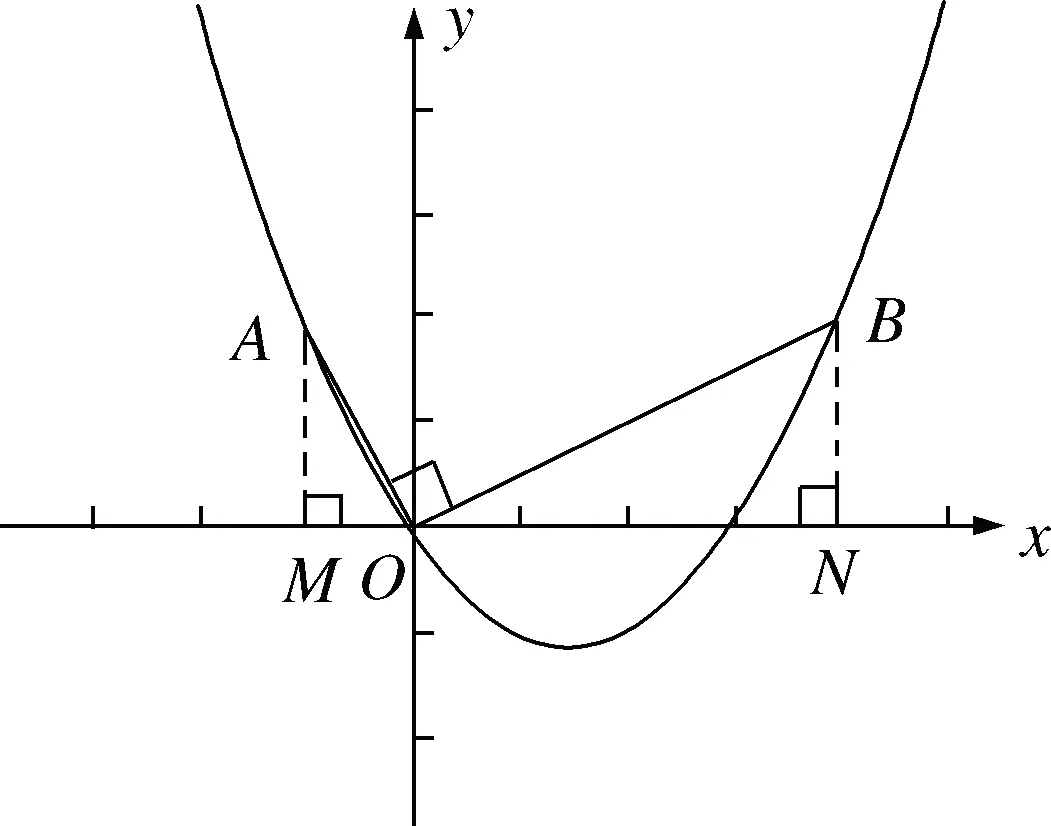
图6
师:问题1中也是构造模型求点B
的坐标,问题1和问题2在解法上有什么区别与联系?生11:两题都是由模型得到△AMO
∽△ONB
,所以区别在于问题1给出了的值,可以求出线段ON
和BN
的长,确定点B
的坐标,问题2无法直接求线段长.
师:那要怎么做呢?
生12:因为点B
在抛物线上,满足抛物线的解析式,所以设则又因为AM
=2,MO
=1,所以解方程,求t
的值,代入得点B
的坐标.
师:很好,抓住点的特殊位置,设坐标列方程来求解,请同学们现在求解一下.
生13:解得t
=4,t
=0.
但当t
=0时,点B
与原点重合,舍去,所以t
=4,得B
(4,2).
师:特别好.
要检验方程的解是否符合题意,再确定最后结果.
本题利用“一线三直角”模型求点的坐标,能总结一下方法吗?生14:可以分五步.
第一步,根据点的特殊位置设坐标;第二步,挖掘题目条件构造模型;第三步,用代数式表示相似直角三角形对应边的长;第四步,由对应边成比例列方程;第五步,解方程,检验,得出结果.
设计意图:
问题2的设计首先让学生能够根据垂直,作图确定点的位置,为接下来直角三角形的存在性问题画图做铺垫.
再通过将本题与问题1进行比较分析,学生感受平面直角坐标系中点的坐标是解题的立足点,也是列方程的关键点,所以要抓住点的特殊位置,用字母表示数设点的坐标,再运用“一线三直角”模型理论解决问题,充分渗透了数形结合和方程思想.
2.4 变式练习,灵活应用
师:通过刚刚两道题的探究,同学们觉得使用“一线三直角”模型的主要条件是什么?
众生:要有直角.
师:看到直角还能想到什么?
众生:直角三角形、矩形、正方形……
师:这些图形都自带直角,为模型的使用提供了必要的条件,将这些图形放到二次函数的背景下又会出现什么新的问题呢?来看下面这道题.
问题3
如图7,抛物线经过原点且与x
轴交于另一点C
,点A
(-1,2)在该抛物线上.
在x
轴上是否存在一点P
,使得以A
,C
,P
为顶点的三角形是直角三角形?若存在,求出点P
的坐标;若不存在,请说明理由.
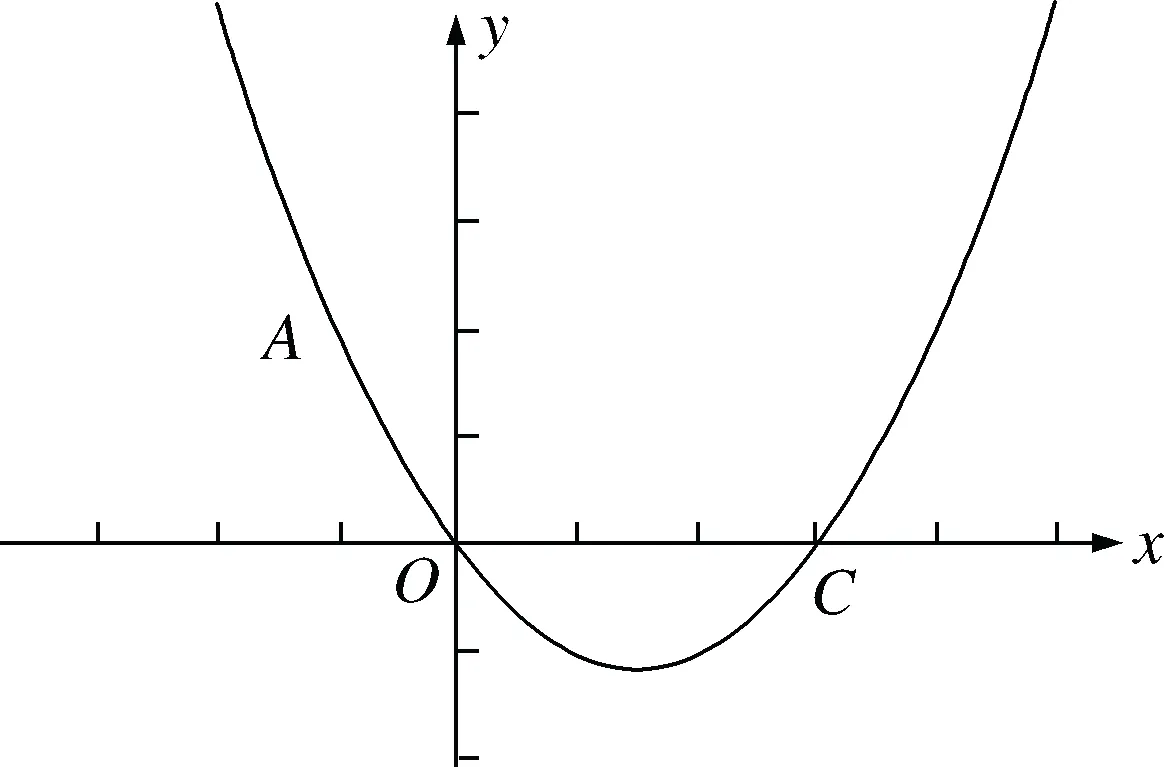
图7
师:本题是直角三角形的存在性问题,该如何处理?
生15:要使△ACP
为直角三角形,需先分类讨论确定点P
的位置.
师:有几种情况?如何分类?
生16:有三种情况,可以按边、角或顶点分类.
师:哪种分类更有利于作图找点P
?请具体说说怎么作图.
生17:按顶点分类最为简便,如图8,联结AC.
(1)若点A
为直角顶点,过点A
作线段AC
的垂线,与x
轴的交点记为P
;(2)若点C
为直角顶点,过点C
作线段AC
的垂线,与x
轴的交点记为P
,情况不存在,舍去;(3)若点P
为直角顶点,则AC
为斜边,以AC
为直径作圆,与x
轴的交点记为P
,此时AP
⊥x
轴.
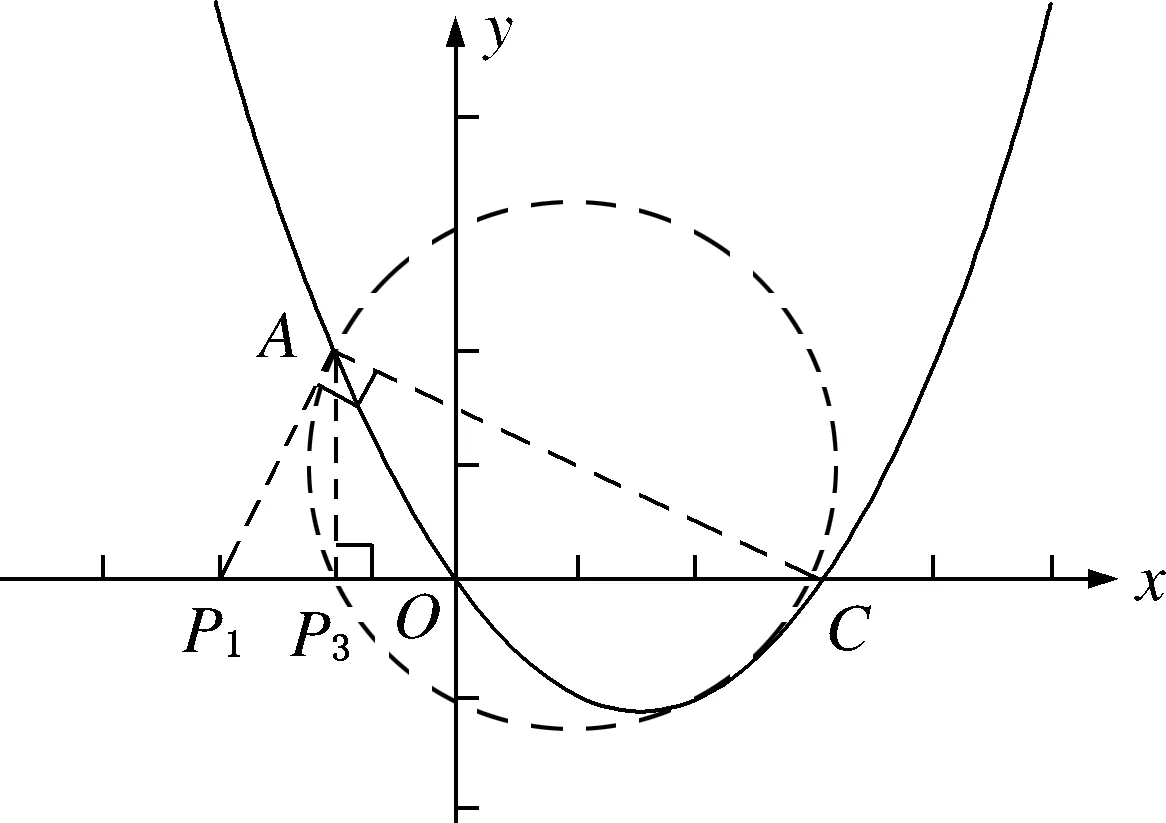
图8
师:确定了点P
的位置后,如何求坐标?生18:根据上题总结的方法,先设点P
的坐标,因为点P
在x
轴上,设P
(t
,0),再通过“找直角、定直线、搭框架”构造“一线三直角”模型.
师:直角很明显,但过直角顶点的直线可以有无数条,要怎么确定?
生19:在平面直角坐标系中,一般过直角顶点作平行于x
轴或平行于y
轴的直线,便于表示点的坐标.
师:非常好,要找“横平竖直”的直线,请简单说说解题过程.
生20:如图9,过点A
作x
轴的平行线,再分别过点P
,C
作平行线的垂线,垂足分别为G
,H
,则四边形CHGP
是矩形.
因为点A
(-1,2),C
(3,0),所以CH
=P
G
=2,AH
=4,AG
=-1-t.
由模型知△AGP
∽△CHA
,得即得t
=-2,所以P
(-2,0).
又因为AP
⊥x
轴,所以P
(-1,0).
综上,当P
(-2,0)或P
(-1,0)时,△ACP
为直角三角形.
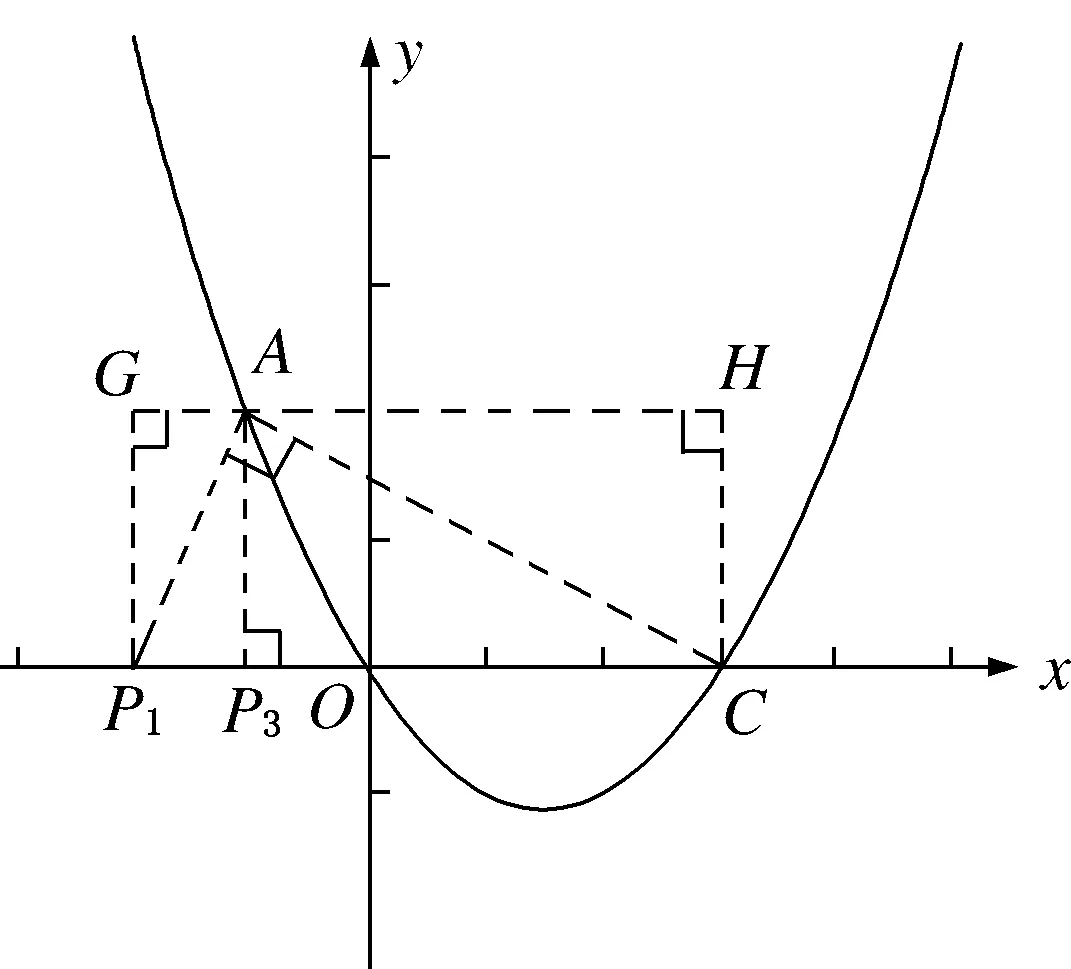
图9
师:还有其他求点P
坐标的方法吗?生21:可以过点A
向x
轴作垂线段,利用射影定理求解,本质上是构造了异侧型“一线三直角”模型.
生22:可以根据AP
⊥AC
得到这两条线段所在直线的比例系数积为-1,通过解析式法求点P
的坐标.
生23:还可以利用两点距离公式表示△ACP
中各边的平方,根据勾股定理列方程求解.
师:很好.
同学们可以尝试不同方法求解,比较方法的优劣,根据不同题目,选择最优解法.
设计意图:
本环节先引导学生根据直角联想到与直角有关的图形,自然地过渡到用“一线三直角”模型来解决图形的存在性问题,同时融入动点,让学生确定直角三角形分类的标准,渗透分类讨论数学思想.
在教学过程中,通过学生作图、师生问答的方式,学生深化对模型构造的理解,把握解题方法.
最后,除了总结得出一般方法外,让学生拓展思路,一题多解,发散思维.
2.5 举一反三,思维拓展
师:问题3中条件不变,你还能提出其他直角三角形的存在性问题吗?
生24:在y
轴上是否存在一点P
,使得以A
,C
,P
为顶点的三角形是直角三角形?若存在,求出点P
的坐标,若不存在,请说明理由.
生25:在抛物线的对称轴上是否存在一点P
,使得以A
,C
,P
为顶点的三角形是直角三角形?若存在,求出点P
的坐标,若不存在,请说明理由.
生26:在抛物线上是否存在一点P
,使得以A
,C
,P
为顶点的三角形是直角三角形?若存在,求出点P
的坐标,若不存在,请说明理由.
师:很好,问题3和这三道题都是典型的直角三角形的存在性问题,请同学们分组求点P
的坐标,并思考这类问题中动点的位置有什么特点?生27:一般在x
轴、y
轴、二次函数对称轴或者函数图像上等,目的是使设点的坐标中只含有一个未知数,或者使横坐标确定,或者使纵坐标确定,或者使横纵坐标之间可以建立联系,这样才能列方程求出未知数的值.
师:问题3条件依然不变,请同学们尝试将直角三角形的存在性问题拓展到四边形.
生28:点P
是对称轴上一点,点Q
为平面内任意一点,是否存在以A
,C
,P
,Q
为顶点的四边形是矩形?若存在,求出点P
,Q
的坐标,若不存在,请说明理由.
师:非常好.
矩形具备平行四边形的特性又含有直角,本质上是将直角三角形的存在性问题与平行四边形的存在性问题相结合,平行四边形的存在性问题前面已经讲过,同学们可以尝试求解.
设计意图:
本环节设置了较为开放性的问题,也提升了一定的难度,让学生站在更高的角度思考问题,从看题、做题到自主编题,对学生的数学素养提出了更高的要求.
直角三角形、矩形、正方形等都是含有直角的图形,通过举一反三,学生抓住这一类问题的特征,形变质不变,最后归纳总结,形成类型问题的完整解题策略.
3 教学思考
3.1 抓住模型特征,渗透模型思想
初中数学的学习离不开数学模型,数学模型来源于对数学规律的总结、知识经验的积累,是基于知识典型结构的特殊总结,因此模型通常具有鲜明特征.
只有抓住模型特征才能正确构建模型得到相应结论,所以在以数学模型建构与应用为主线的复习教学中有两个重点:一是抓住模型特征,二是渗透模型思想.
本节课在提炼模型环节给了学生充分表达的机会,让学生进行特征总结,理解模型结构,为后续顺利构建模型和应用模型做铺垫.
而模型思想的渗透属于更高层面,需要教师在平时的教学中有意识地带领学生体验建模过程,指导学生建模方法,从模型的角度思考问题,从根本上提升数学素养.
3.2 关注知识生长,构建整体结构
《义务教育数学课程标准》指出:数学知识的教学,要注重知识的“生长点”与“延伸点”,把每堂课所要教授的知识置于整体知识的体系中,注重知识的结构和体系.
本节课以“一线三直角”模型的提炼、构建及应用为主线,问题设计以同一条抛物线为载体,让学生在整体上搭建知识框架.
而从局部上看,将模型教学与其他知识点相串联,层层铺垫,形成一条问题链,逐步让学生掌握解题方法和解题思路.
最后又引导学生对题目进行拓展,举一反三,培养学生高水平思维能力,让知识得以自然地生长与延伸.
3.3 重视归纳总结,增进复习实效
模型教学的复习课中,对数学思想和数学方法的总结也尤为重要.
本节课的探究过程中教师引导学生进行了四次归纳总结:一是挖掘模型特征,总结构建模型的三步法;二是对比问题条件,总结抛物线中求点的坐标的五步法;三是让学生自主作图,总结直角三角形三种分类标准;四是运用模型解决问题的过程中,总结二次函数中存在性问题模型.
通过及时归纳总结帮助学生关注细节,掌握完整的模型解题过程,认识问题的本质规律,达到“知一法,通一类”的效果,增强复习实效.
