基于直观想象与数学运算素养培育*
——向量题几何背景挖掘与构造
2022-08-04734500甘肃省民乐县第一中学赵思博
中学数学 2022年5期
734500 甘肃省民乐县第一中学 赵思博
向量本身兼具“形”与“数”的双重特性,是解决代数问题和几何问题的有力工具,加上其本身的内容十分丰富,命题形式灵活多变,自然成为高考命题的热点.
近年来,高考对向量的综合运用的考查多与平面几何、解析几何、不等式等相结合进行交汇命题,综合性强,难度较大,学生在这类问题上得分也不理想.
笔者认为,向量教学要逐步让学生体会“从形到向量—借助向量运算解决问题—从向量到形”的“三部曲”,更要培养学生逆向思考,体会“从向量到形—借助几何直观优化运算—从形到向量”的“三部曲”.
根据教学实践和解题研究,笔者阐述解决具有一定几何背景的向量问题的有效策略.
1 直观建模,以数思形解三角形最值问题
例1
(2010高考浙江理-16) 已知平面向量满足且与的夹角为则的取值范围是________.
解:
由联想到向量减法的三角形法则,构造△CAB
,作向量则向量在△CAB
中,边利用正弦定理得所以可得评注:
此题以向量减法为背景巧妙命题,利用向量的几何意义把符号表示形式转化为图形表达形式,使问题求解变得直观.
在向量的意义及运算体系建立后,要注意强化向量的几何直观表示,引导学生体会通过建立向量符号运算与几何图形之间的关系,形成解决向量题的背景支持.
例2
(2013浙江理-17) 设为单位向量,非零向量若的夹角为则的最大值等于________.
解:
不妨设则在△OAB
中,又的夹角为则或即则评注:
此题考查平面向量基本定理、平面向量的几何意义及向量的运算.
通过向量加法运算构建三角形,使题目形象鲜明,直观具体,思路豁然开朗.
构建数学问题的直观模型,将向量“图形化”,借助图形把问题的本质凸显出来,通过几何直观感知数学抽象,理解运算对象,使问题变得简明、形象.
2 构图建系,巧用矩形性质以形解数
例3
(2013重庆理-10) 在平面上,若则的取值范围是( )解法1:
根据条件知A
,B
,P
,B
构成一个矩形,便于建立坐标系,利用坐标法解决.
以AB
,AB
所在直线为坐标轴建立平面直角坐标系(如图1所示).
设|AB
|=a
,|AB
|=b
,点O
的坐标为(x
,y
),则点P
的坐标为(a
,b
),由得则又由得则所以而所以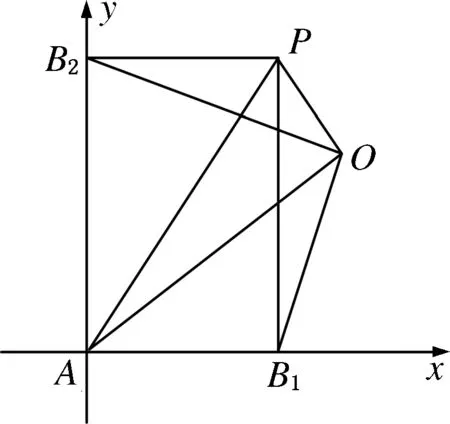
图1
解法2:
由由两个条件结合向量加法的平行四边形法则,易得矩形AB
PB
,O
是平面内一动点,联结OA
,OP
,OB
,OB
,则有OA
+OP
=OB
+OB
(矩形的一个性质,可证明),所以可得的取值范围是评注:
此题以平面向量加法的平行四边形法则和矩形为几何背景命题,在易于建立坐标系的情况下,优先考虑坐标运算,向量的坐标表示为实现向量运算到数的运算打下了基础,建立起了几何与代数之间的联系,在向量问题解决中突出坐标法,是要让学生感悟用坐标法研究几何问题的程序性和普适性.
解法2结合图形特征应用矩形的性质大大简化了运算,数形结合是几何图形的代数表达,也是代数表达式的几何直观,作为数形结合的两个方面,两者都不可或缺.
向量教学中既要重视几何图形的代数表达,也要关注代数表达式的几何直观,利用几何直观,发挥图形的功能,有助于向量问题的解决.
3 直观显化,巧用圆的性质避繁就简
例4
(2014安徽理-10) 在平面直角坐标系xOy
中,已知向量点Q
满足曲线区域若C
∩Ω
为两段分离的曲线,则( )A.
1<r
<R
<3 B.
1<r
<3≤R
C.r
≤1<R
<3 D.
1<r
<3<R
解法1:
作向量并且OA
⊥OB
,设则则由此可得曲线C
是以O
为圆心、1为半径的圆.
区域Ω
是以Q
为圆心的圆环,内圆半径为r
,外圆半径为R
′,若C
∩Ω
为两段分离的曲线,结合图形可知,半径为r
和半径为R
的两圆均与以O
为圆心1为半径的圆相交,所以1<r
<R
<3.
解法2
(坐标法):不妨设易得以下同解法1.
评注:
此题以平面向量加法的平行四边形法则和圆为几何背景命题,解题的关键是能正确分析出曲线C
和区域Ω
是什么样的图形.
面对如此之多的抽象数学符号,很多学生束手无策,若能认真分析集合内元素的本质特征,细心挖掘其具体意义和几何背景,将抽象的符号语言直观显化,并能数形结合分析其数量关系,即可顺利完成解答.
有些数学表达式是有明显几何意义的,从几何图形的直观认识问题的实质,进而解决问题往往运算较简便,但这种方法构造性强,需要较高的思维水平和对向量的深入认识及理解.
例5
(2016四川理-10) 在平面内,定点A
,B
,C
,D
满足动点P
,M
满足则的最大值是( )解:
由题意,所以D
到A
,B
,C
三点的距离相等,D
是△ABC
的外心.
由得所以DB
⊥AC
,同理可得DA
⊥BC
,DC
⊥AB
,从而D
是△ABC
的垂心.
△ABC
的外心与垂心重合,因此△ABC
是正三角形,且D
是△ABC
的中心.
求得所以正三角形△ABC
的边长为解法1:
如图2所示,以A
为原点建立直角坐标系,B
,C
,D
三点的坐标分别为由动点P
的轨迹是单位圆,设P
点的坐标为(cosθ
,sinθ
),其中θ
∈[0,2π),而即M
是PC
的中点,可以写出M
的坐标为则当时,取得最大值故选B.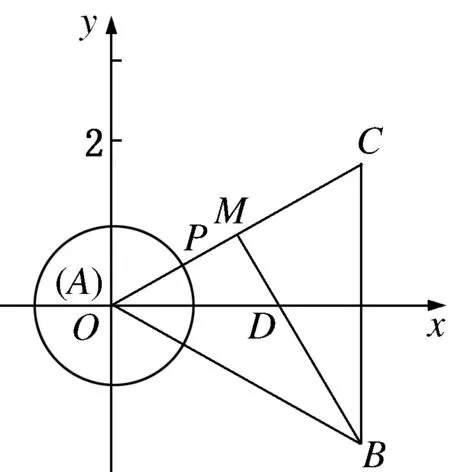
图2
也可以以点B
为坐标原点,BC
所在直线为x
轴建立直角坐标系(如图3所示)由点P
的轨迹方程为令点又即M
是PC
的中点,则取得最大值为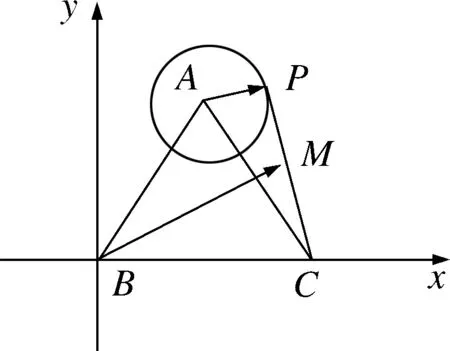
图3
解法2:
取AC
的中点从而动点M
的轨迹是以N
为圆心为半径的圆,当B
,N
,M
三点共线时,BM
为最大值.所以BM
最大值为则取得最大值评注:
本题考查了数量积运算性质、平面向量的数量积与向量的模、圆的参数方程、三角函数求值,考查了推理能力与计算能力.
对条件进行化简变形,易得出△ABC
是正三角形,动点P
的轨迹是圆,动点M
的轨迹也是圆,解法1运用坐标法,转化为三角函数的最值的求法,使学生对向量运算的认识逐步深化,进一步体会向量的主要作用要通过运算来实现.
解法2利用圆的性质得出最值,则更能体现向量运算的几何解释.
4 以形助数,妙用圆的性质化动为定
例6
(2014湖南文-10) 在平面直角坐标系中,O
为原点,动点D
满足则的取值范围是( )解:
此题中已有坐标系,为三定点,可设动点D
(x
,y
),则所以有(x
-3)+y
=1,说明点D
的轨迹是以C
(3,0)为圆心、1为半径的圆.
因则有此式有明确的几何意义,表示定点到圆C
上点的距离,数形结合可求得其取值范围是评注:
此题以平面向量的坐标运算和解析几何中两点间的距离为几何背景命题,巧妙地把向量的坐标形式转化为图形形式,使解题事半功倍,优化了解题过程.
研究向量问题要树立数形结合思想和坐标法统领全局的意识,解决问题时要善于用坐标法运算,用几何眼光观察与思考,用代数表达式的几何直观解决问题,从而促进学生的数学运算、直观想象等素养的发展.
5 深度理解,利用几何直观化繁为简
例7
(2013安徽理-9) 在平面直角坐标系中,O
是坐标原点,两定点A
,B
满足则点集所表示的区域的面积是( )解法1:
要求面积应先明确是怎样的图形,从题设提供的信息想到建立坐标系,寻求动点坐标满足的线性约束条件,将问题转化为不等式组表示的平面区域.
由可得建立直角坐标系,可设可得则当时,由可行域可得由对称性可知区域的面积是所以选D.
解法2:
由可得可知△OAB
是一个边长为2的等边三角形,由考虑当λ
≥0,μ
≥0,且λ
+μ
=1时,A
,B
,P
三点共线(用三点共线的充要条件可判断),则λ
≥0,μ
≥0,且λ
+μ
≤1时,点P
必在△OAB
内(包括边界),考虑|λ
|+|μ
|≤1,λ
,μ
∈R
的其他情形,点P
的集合恰好是以AB
为一边,以OA
,OB
为对角线一半的矩形,其面积评注:
解法1从坐标的角度考虑,先建立平面直角坐标系,利用题设条件得点P
的坐标x
,y
与λ
,μ
之间的关系,利用|λ
|+|μ
|≤1,λ
,μ
∈R
得到关于x
,y
的不等式组,将问题转化为线性规划问题解答,这是典型的坐标法,是研究解析几何问题最基础、最常用的方法,完全通过代数运算,运算量较大,得到最终结果需要较强的数学运算能力,这对提升学生的数学运算素养是有利的.
解法2从平面向量基本定理入手,结合三点共线的充要条件去思考构成平面点集的区域图形的形状,巧妙地避开了繁杂的运算,不失为一种优美解法,但这种方法体现较强的构造性,对学生的思维水平要求较高,要求学生对向量知识有系统的认识和深入的理解.
数学问题求解的基本思维方法是从题设条件出发寻找解题的方向.
在决断解题方法时,对题设条件的思维切入点不同,解题的方法也将不尽相同.
对于一类有几何背景的向量题,在寻找解题思路时,应牢牢把握向量的两个基本特征:利用“数”的特征,可以从向量的线性运算、数量级、基底分解与坐标运算等方面切入,将问题转化为代数运算来解决;利用“形”的特征,通过向量的几何意义及向量的运算将其转化为平面几何中的问题,直接利用平面几何中的相关结论得到结果.
教师在教学中,要注重直观想象与数学运算素养的培养,这样学生才能熟练地实现向量的符号表示形式向图形表达形式、坐标表示形式的转化,优化向量问题解法.
