利用角双缝干涉测量涡旋光束拓扑荷综述*

付栋之,张 静,张营堂,张 沛

(1.河南工学院 电缆工程学院,河南 新乡 453003;2.西安交通大学 物质非平衡合成与调制教育部重点实验室,陕西 西安 710049)

0 引言

光子除具有自旋角动量外,还具有轨道角动量(Orbital Angular Momentum,OAM)[1]。光子的OAM和复电场的螺旋相位exp(ilφ)有关[2,3]。φ是方位角,l是涡旋光束拓扑荷(Topological Charge,TC),也称为轨道角动量量子数,其可以取任意的整数,每个光子可以携带lћ的OAM。在宏观上,光子的OAM表现为涡旋光场的横向空间分布模式,其等相位面沿光束传播方向呈现螺旋变化,导致在传播轴上有一个相位奇点,横向光强分布的中心有一个暗斑,因而被称为涡旋光场。涡旋光场的高维和涡旋特性使其在量子计算[4-6]、高维量子信息[7-8]、高密度通信[9-13]、图像编码[14]、光学粒子操纵[15-18]和探测旋转微粒或旋转物体的角速度[19-20]等方面具有诱人的应用前景。

与传统涡旋光束(TC为整数)相比,分数阶涡旋光束具有特殊的特性[21]。一个分数阶涡旋光束在它的传播过程中的相分布为exp[i(Mφ+β)],M是分数阶涡旋光束TC,其可以取任意的分数,β是螺旋波前切割的角位置(角相位不连续)。由于分数阶涡旋光场的径向相位不连续,打破了整数阶涡旋光场的轴向强度对称性,导致强度分布出现径向开口[21,22]。分数阶涡旋光场不是OAM算符的本征态,而是OAM基矢的叠加态[23-25]。由于这些特性,分数阶涡旋光束在粒子操控[26]、提高光学分选能力[27]、高维量子纠缠[23,28-29]、自由空间光通信[30]等方面具有许多特有的优势。

无论是整数阶涡旋光束还是分数阶涡旋光束,在应用前对其TC精确测量是必要的,这也是其在经典和量子信息领域应用的基础之一,如在利用光子OAM作为载体进行量子信息处理中,最后解码信息时必须对每个光子的OAM进行准确测量。目前关于整数阶涡旋光束TC的测量有多种方法[9,31-33],主要分为两大类:一类是将涡旋光场经过特殊的相位和振幅变换,根据衍射光场的特征判断TC,如双缝干涉[34-36],根据干涉图样中条纹从顶部到底部的扭曲个数及方向来确定TC;另一类方法是通过干涉或衍射,使OAM模式与空间路径耦合,可直接探测单光子水平下的TC,如Mach-Zehnder干涉仪法[37,38],利用Dove棱镜在干涉仪两臂引入与TC有关的相位差,进而将具有不同TC的光子分到不同出口。这些方法中有些只能用于测量整数阶涡旋光束TC,但有些方法同样适用于测量分数阶涡旋光束TC[38-45],如Mach-Zehnder干涉仪法、角双缝干涉法。

本文针对常见的涡旋光场:拉盖尔-高斯(Laguerre-Gaussian,LG)光束、贝塞尔光束和完美涡旋(perfect optical vortex,POV)光束,综述利用角双缝测量涡旋光束TC的方法[45-51]。首先,根据涡旋光场相位的周期性,分析角双缝测量涡旋光束TC的理论;其次,针对LG光束、贝塞尔光束和POV光束,以整数阶涡旋光束与分数阶涡旋光束两类形式,论述利用角双缝测量其TC的研究结果及发展现状;最后,对利用角双缝测量涡旋光束TC的方法进行总结与展望。

1 角双缝干涉测量涡旋光束TC的理论分析

常见的涡旋光场有LG光束、贝塞尔光束和POV光束。LG模式是亥姆赫兹方程在柱坐标系下的正交完备解,其具有两个指数:径向量子数p∈{0,1,2,…}和角向量子数l∈{0,±1,±2,…},径向结构主要由径向指数p决定,而螺旋相位结构则由角向指数l(轨道角动量量子数、涡旋光束拓扑荷)描述,如图1(a)和(b)所示。p和l的结合可以完整描述光场的横向状态空间,即LG模式构成了一个无限维的希尔伯特空间[52]。贝塞尔光束是Durnin在1987年用数学方法提出的自由空间旁轴波动方程的一组解[53,54],其具有螺旋相位exp(iMφ),M为贝塞尔光束的TC,其可以是任意的实数(整数或分数)。贝塞尔光束具有无衍射或传播不变性[55,56]、自重构[30,57]以及强度的环结构理论无穷大等特性。整数阶的高阶贝塞尔光束(|M|> 0)有一系列同心圆环,中心有一个圆形暗斑,而分数阶的贝塞尔光束在同心圆环中有一个低强度的径向带[21,58],如图1(c)和(d)所示。2013年Ostrosky提出了POV光束的概念[59],理论上,对理想贝塞尔光束进行傅里叶变换可以得到POV光束[60]。常规涡旋光束(如LG光束和高阶贝塞尔光束)的径向强度分布与TC有关,而POV光束的径向强度分布与TC无关,如图1(e)和(f)所示。另外,由于分数阶涡旋光场的角相位不连续,打破了整数阶涡旋光场的轴向强度对称性,导致强度分布出现径向开口,如图1(d)和(f)所示。

图1 (a)TC=4的LG光束相位分布 (b)TC=4的LG光束光强分布 (c)TC=4的贝塞尔光束光强分布 (d)TC=4.5的贝塞尔光束光强分布 (e)TC=4的POV光束相位分布 (f)TC=4.3的POV光束相位分布

根据文献[48]和[49]可知,当一束涡旋光束经过角双缝时,只有角双缝处的光强透过,因此,远场的干涉图样取决于角双缝间的相位差。角双缝干涉原理图如图2所示,其中,θ代表在其中一个角单缝上加的附加相位。两个具有相同角宽度α的角单缝所在的入射平面是xoy平面,观察平面x′o′y′与入射平面xoy平行,q1、q2和q3分别是两个角单缝及它们角平分线上的一点,φ1和φ2是两个角单缝的角位置,Δφ=φ2-φ1是两个角单缝间的夹角。当一束涡旋光束沿z轴经过角双缝后,由于入射涡旋光束的螺旋相位结构和角双缝到观察平面x′o′y′的光程差,导致在x′o′y′平面会出现明暗相间的干涉图样。假设两个角单缝在观察平面p点的电场分别为

E1(p)=u(p)exp[iφ1(p)]

(1)

E2(p)=u(p)exp[iφ2(p)]

(2)

其中,u(p)和φ(p)分别是振幅和相位。则角双缝在点p的干涉强度分布为

I(p)=|E1(p)+E2(p)|2

=|u(p)exp[iφ1(p)]+u(p)exp[iφ2(p)]|2

∝1+cos(Δφ)

(3)

其中,Δφ是角双缝到点p的相位差,由图2可知

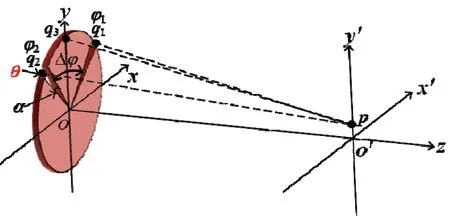
图2 角双缝干涉原理图

(4)

其中,λ是入射涡旋光束的波长,公式中等号右边第一项l·Δφ是由涡旋光束的螺旋相位结构引起的相位差,等号右边第二项是由几何光程差引起的相位差。由公式(3)和(4)可知,若Δφ=Nπ(其中N为整数),当N为偶数时,在p点出现相干相长的干涉图样,当N为奇数,在p点出现相干相消的干涉图样。

若角双缝关于o′p轴对称,即o′p轴平行于角双缝的角平分线oq3,那么角双缝到点p由几何光程差引起的相位差为零,则角双缝到点p的相位差只依赖于由螺旋相位引起的相位差,即Δφ=l·Δφ,则干涉强度分布变为

I=|E1+E2|2∝[1+cos(l·Δφ)]

(5)

由公式(5)可以看出,强度分布与涡旋光束TC乘以角双缝间的夹角Δφ的余弦成正比关系,因此,可以通过Δφ-I曲线识别入射涡旋光束TC的模值。其有以下三种方法:1)将oq1固定在x轴(φ1=0),oq2由-π连续变到π,当角双缝的夹角发生变化时,远场干涉图样的强度也随之变化,其中干涉图样的Δφ-I曲线的可见度作为角双缝夹角Δφ的函数等价于场的角关联函数,通过对双角缝干涉得到的角关联函数进行傅里叶变换,可以计算出部分相干场的OAM谱[46];2)将oq1固定在x轴(φ1=0),oq2由0连续变到2π,o′p永远在角双缝角平分线方向,若o′p上强度变化周期为2φ0(角度周期:o′p轴的强度由相干相长变为相干相消或由相干相消变为相干相长时,角双缝间的夹角变化为φ0),则入射涡旋光束TC的模值为l=π/φ0,但是当l=0时,o′p轴上总是出现干涉加强的图样[47];3)将oq3固定在y轴,两个角单缝从y轴以相同的角速度向相反的方向旋转,当角双缝间的夹角Δφ由0变到2π时,则p点的干涉图样强度变化的周期(2π内变化的次数)就等于入射涡旋光束TC的模值[45, 48-51]。

由公式(5)可以看出,由于余弦函数是偶函数,因此,无法判断入射涡旋光束TC的正负。测量TC的正负可通过以下三种方法实现:1)第一种方法是通过干涉图样由干涉相长向干涉相消过渡时的变化趋势来判断TC的正负,即正负TC的干涉图样向相反方向移动[47];2)第二种方法是在其中一个角单缝上加一个附加相位θ来实现,此时角双缝间的相位差变为

Δφ=l·Δφ+θ

(6)

干涉强度的分布为

I∝[1+cos(l·Δφ+θ)]

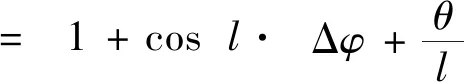
(7)

由公式(7)可知,附加相位会引起Δφ-I曲线的旋转,旋转角度为θ/l,旋转的方向和TC的正负有关[45,49];3)第三种方法是通过绘制Δφ-I正弦曲线来实现,即

I∝1-sin(l·Δφ)

(8)

由公式(5)和公式(8)可知,Δφ-I正弦曲线相对Δφ-I余弦曲线发生了π/2l旋转,旋转的方向和TC的正负有关,因此,可通过观察Δφ-I正弦曲线相对于Δφ-I余弦曲线的旋转方向判断TC的正负[51]。当入射光束为分数阶涡旋光束时,即TC为任意分数时,利用角双缝干涉同样可以测量其TC[45,50,51]。一个分数阶涡旋光束在它的传播过程中的相分布为exp[i(Mφ+β)],M是分数阶涡旋光束的TC,其为任意的分数,β是螺旋波前切割的角位置(角相位不连续)。在p点采集强度后,可以得到Δφ-I曲线,则可以通过拟合得到M的值,拟合函数可选择为

I0=a0+a1sin(Mtφ)+b1cos(Mtφ)

(9)

其中,a0、a1和b1为背景光对强度的影响。为了使拟合误差最小,公式(9)中的任何参数都不固定。采用加权最小二乘拟合法得到式(9)中的参数。拟合方法将自动调整所有参数,使其达到最小误差平方和,并输出a0、a1、b1和Mt值。其中参数Mt与TC相关,是我们关心的参数,其他的可以忽略。M的正负可以用测量整数TC同样的方法获得。

2 实验结果与讨论

角双缝干涉测量涡旋光束TC的实验装置图如图3所示。一束He-Ne激光经两个透镜L1和L2扩束后入射到利用计算机生成全息图的空间光调制器(spatial light modulator,SLM)上,涡旋光束图3中的插图显示了加载在SLM上的掩膜,该掩膜由一个角双缝和一个产生高阶LG光束/贝塞尔光束/POV光束的全息光栅组合而成,此处涡旋光束和角双缝由同一个SLM产生,也可以将生成涡旋光束的叉形光栅与角双缝由不同的SLM产生,即两者处于不同的空间位置。用小孔选出一级衍射光斑,然后用电荷耦合器件(charge coupled device,CCD)采集远场干涉图。

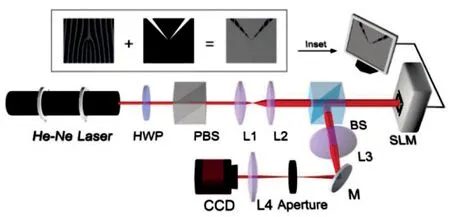
图3 实验装置图[49](插图显示了加载在SLM上的掩膜)

2.1 利用角双缝干涉测量整数阶涡旋光束TC

角位置及其共轭变量OAM形成了傅里叶变换对[61-63],对于LG模式的部分角相干场,OAM模谱仅仅是角相干度的傅里叶变换[64]。基于此,2012年Mehul Malik提出利用角双缝干涉测量部分角相干场的OAM谱[46]。文献[46]中的实验,角双缝的角宽度为15°,其中一个角单缝oq1固定在x轴上(φ1=0),另一个角单缝oq2由-π连续旋转到π(φ2由-π变到π)。在远场的干涉图样中选p点附近的一个矩形区域为干涉强度采集区域,对采集区域强度积分得到干涉强度的Δφ-I变化曲线。实验结果如图4所示,图4(a)—(c)角相干度依次减小,其中黑色虚线为实验数据,红色实线由理论拟合所得[46],绿长虚线表示拟合的可见度包络线。由图4(a)可知,当入射涡旋光束只有一个OAM模式时(完全角相干场TC=12),在笛卡尔坐标系中Δφ-I曲线的峰值个数就等于入射涡旋光束TC,且对于任意的Δφ,Δφ-I曲线的可见度包络线都接近于1。当入射涡旋光束中含有多个OAM模式时(部分角相干场:角相干度为(b)0.71和(c)0.29),随着角相干度降低,Δφ-I曲线包络线变窄,如图4(b)和(c)所示,入射涡旋光束中OAM模式呈高斯分布,且图4(c)的角相干度低于图4(b)。通过对图4(b)和(c)中的角关联函数(图中绿色长虚线所对应的函数,即干涉图样的可见度随Δφ的变化,其中可见度包络线的宽度可以作为光源角相干度的直接度量)进行傅里叶变换,可以得到入射涡旋光束的OAM谱,如图5(a)和(b)所示。

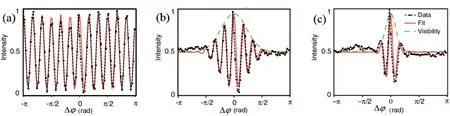
(a)完全角相干场 (b)部分角相干场,角相干度为0.71 (c)部分角相干场,角相干度为0.29图4 不同OAM态的归一化强度变化曲线[46]

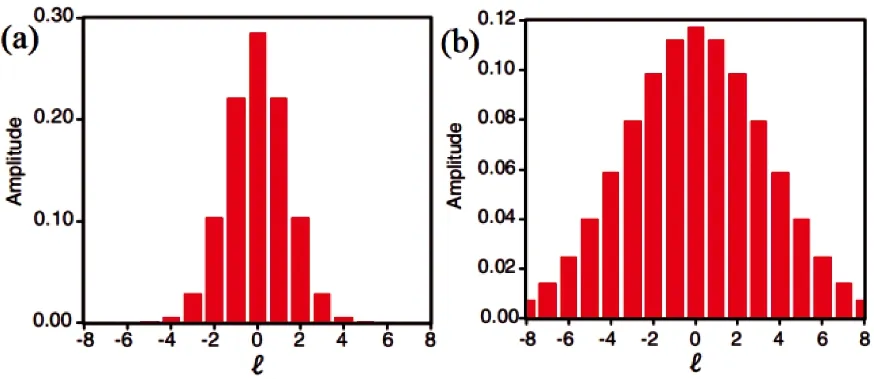
图5 计算得到的OAM谱分布[46]

文献[46]测量的是具有部分角相干场的OAM谱,文献[47]提出通过记录角双缝干涉的远场干涉图样,直接识别LG光束的TC(角向指数l)。在文献.[47]的实验中,角双缝的角宽度为10°,一个角单缝oq1固定在x轴上(φ1=0),另一个角单缝oq2由0连续旋转到2π(φ2由0变到2π),o′p随oq2旋转而旋转,且o′p与x轴的夹角为φ2/2=Δφ/2。角双缝干涉的实验结果如图6和图7所示。图6中的虚线表示对具有不同TC的涡旋光束,干涉图样在o′p上为干涉相长和干涉相消时的方向,且虚线的倾斜角为角双缝夹角的一半,即为Δφ/2。但当入射涡旋光束TC为0时,在o′p方向上总能得到干涉相长的图样。TC不为0时,其模值可由l=π/φ0得出,其中2φ0为o′p轴上强度变化的周期,图6中第一行与第二行两个Δφ之差等于φ0。图7显示当入射涡旋光束TC为l=+4和l=-4时,随角双缝间夹角变化而变化的干涉图样。从理论结果和实验结果中可以看出,对于携带相反符号的TC,干涉图样在干涉相长和干涉相消之间过渡时有相反的变化趋势,即正负TC的干涉图样向相反方向移动。例如,当角双缝间的夹角Δφ由0变到π/2时,l=+4时,干涉图样从下半部移动到上半部;而l=-4时,干涉图样从上半部移动到下半部。

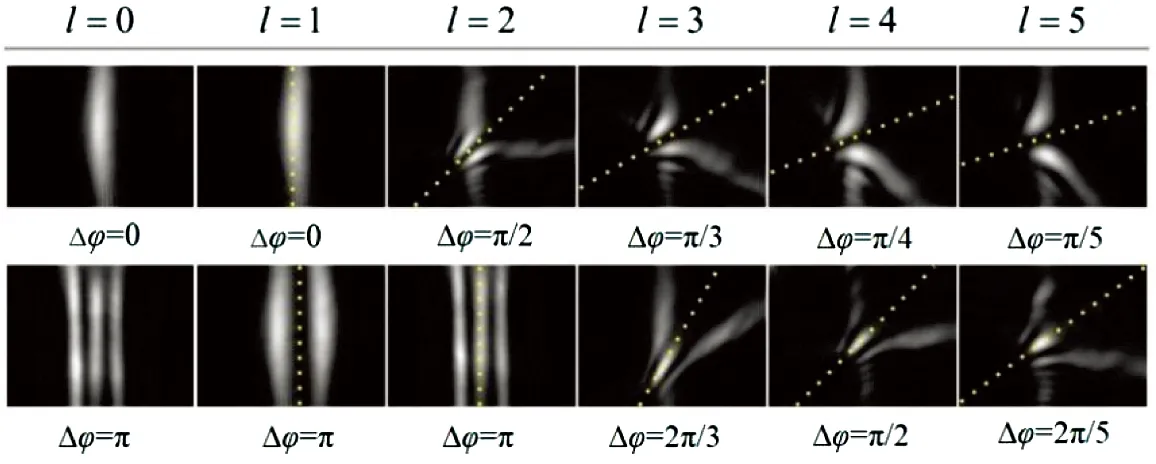
图6 不同TC下角双缝干涉图样的实验结果[47],插图中的虚线倾斜角度为Δφ/2

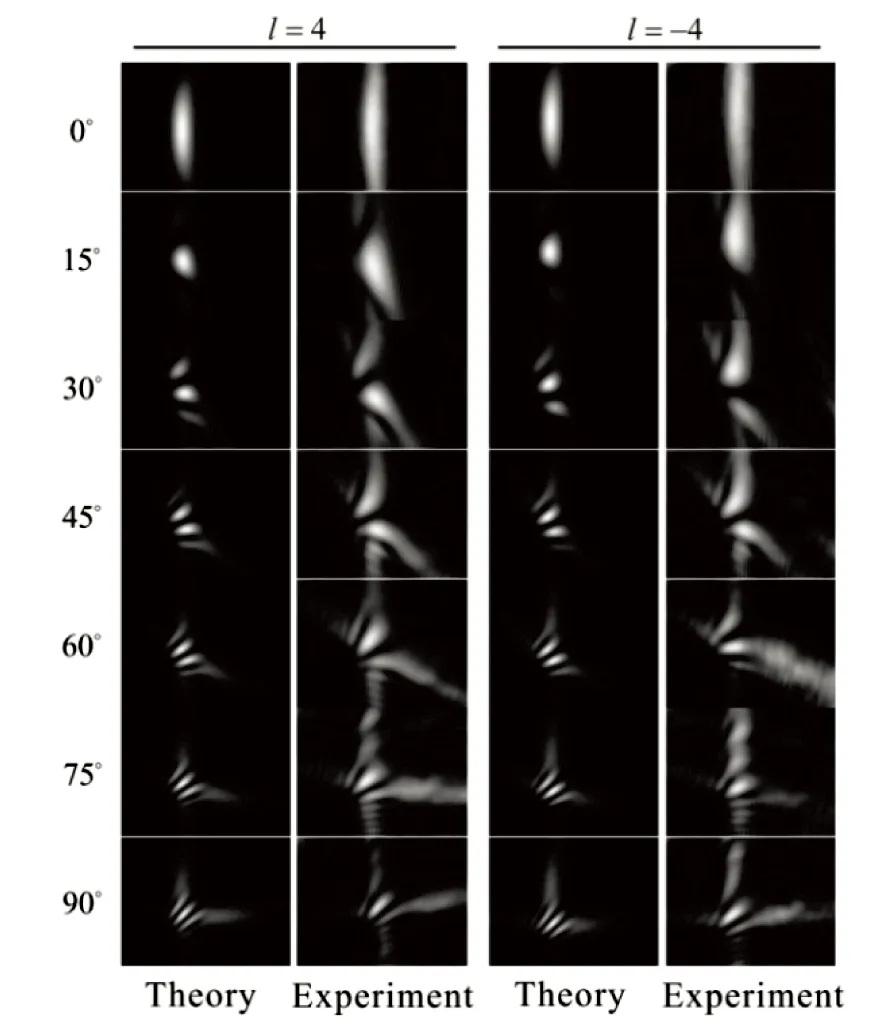
图7 TC为l=±4时的角双缝干涉图样[47],第一列和第三列为理论模拟结果,其他为实验结果

在文献[47]和[48]的基础之上,文献[49]中提出了更简单的测量LG光束TC的方法。在文献[49]实验中,角双缝的角宽度为8°,角双缝的角平分线固定在y轴上,则干涉图样的中心在y轴上微小移动,o′p与y轴重合。选原点附近的干涉图样为干涉强度采集区域,对采集进行区域强度积分得到干涉强度的Δφ-I变化曲线。角双缝干涉实验结果如图8所示,其中绿色Δφ-I曲线无附加相位,只能从其强度变化的周期中得到TC的模值;蓝色Δφ-I曲线是在其中一个角单缝上加附加相位θ=π/2而得到的曲线,且蓝色曲线相对绿色曲线发生了旋转,ΔΨ为旋转角度。由图8可以发现当TC为正时(第一行),旋转方向为顺时针;反之,当TC为负时(第二行),旋转方向为逆时针。

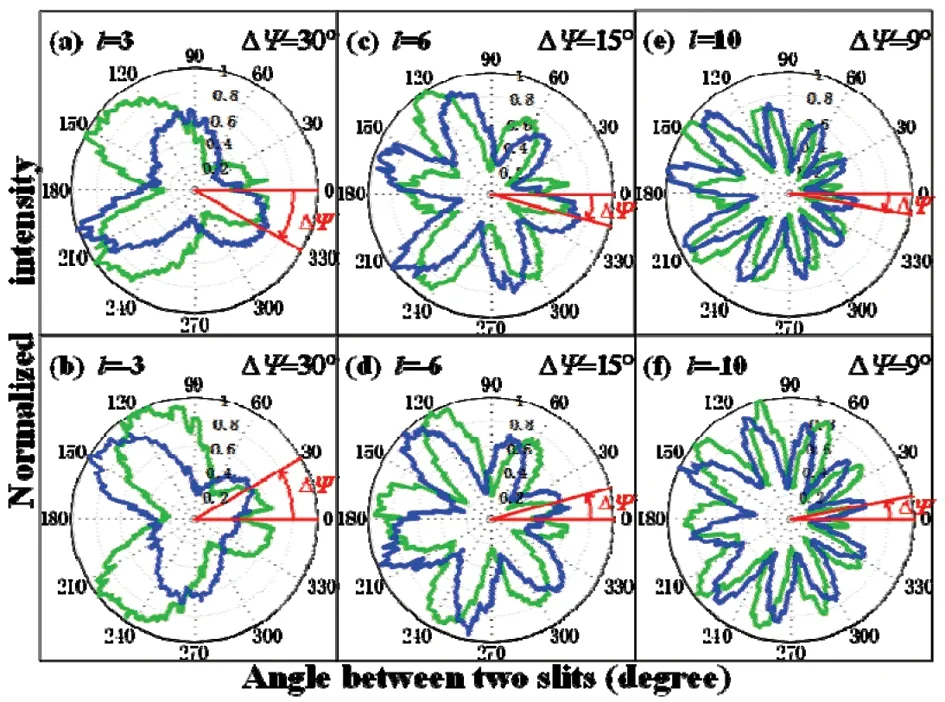
图8 不同OAM态的强度变化曲线及有附加相θ=π/2时在极坐标下的Δφ-I旋转曲线[49]

2.2 利用角双缝干涉测量分数阶涡旋光束TC

文献[45]中将角双缝方法拓展到测量分数阶涡旋光束的TC。实验结果如图9和图10所示。图9为不加附加相位的实验结果图,黑点为实验数据,绿色曲线为实验数据拟合结果。M是分数阶TC的理论值,Mf是利用实验数据由拟合函数用加权最小二乘拟合法拟合出的测量值,在实验中M和Mf之间的误差小于5%。在图10中,M=4.3,蓝色Δφ-I曲线未加附加相位,紫色Δφ-I曲线加了附加相位,与蓝色Δφ-I曲线相比,紫色Δφ-I曲线顺时针旋转;相反,当分数阶涡旋光束TC为负时(M为负),紫色Δφ-I曲线将逆时针旋转。

图9 当附加相位θ为零时,在极坐标下的Δφ-I曲线[45]

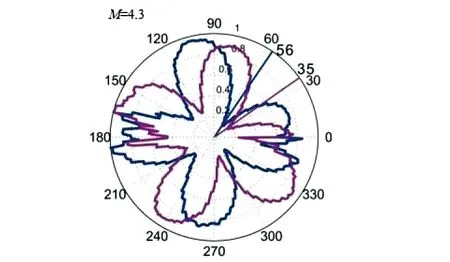
图10 当M=4.3时,对比θ=0(蓝色曲线)与θ=π/2(紫色曲线)时的Δφ-I曲线[45]

在之前工作基础上[45,49],发展了利用角双缝测量贝塞尔光束的TC[50]。图11为实验结果,黑点代表实验数据,灰绿色曲线是拟合结果。M是理论值,Mf是利用实验数据由拟合函数用加权最小二乘拟合法拟合出的测量值,在实验中M和Mf之间的误差小于2%。对于贝塞尔光束TC的正负, 依然可以利用附加相位,通过Δφ-I曲线的旋转方向来判断。

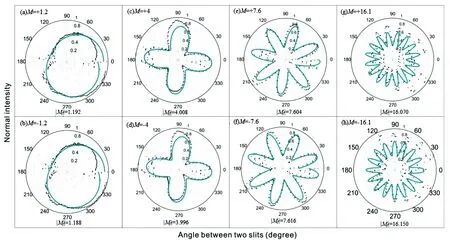
图11 极坐标下的Δφ-I曲线[50]。黑点为实验数据,灰绿色实线由实验数据拟合所得

利用角双缝方法测量了POV光束的TC[51],实验结果如图12和图13所示。图12中蓝色填充的小方块是实验数据,红色曲线为拟合的Δφ-I曲线。M是理论值,Mf是利用实验数据由拟合函数用加权最小二乘拟合法拟合出的测量值,在实验中M和Mf之间的误差小于2%。图13是识别M正负的实验结果图,绿色曲线是Δφ-I余弦函数曲线,粉色曲线是Δφ-I正弦函数曲线。根据公式(5)和(8)可知,Δφ-I正弦曲线相对于Δφ-I余弦曲线发生了旋转。当M的符号为正时,Δφ-I正弦曲线顺时针旋转;相反,当M的符号为负时,Δφ-I正弦曲线逆时针旋转。

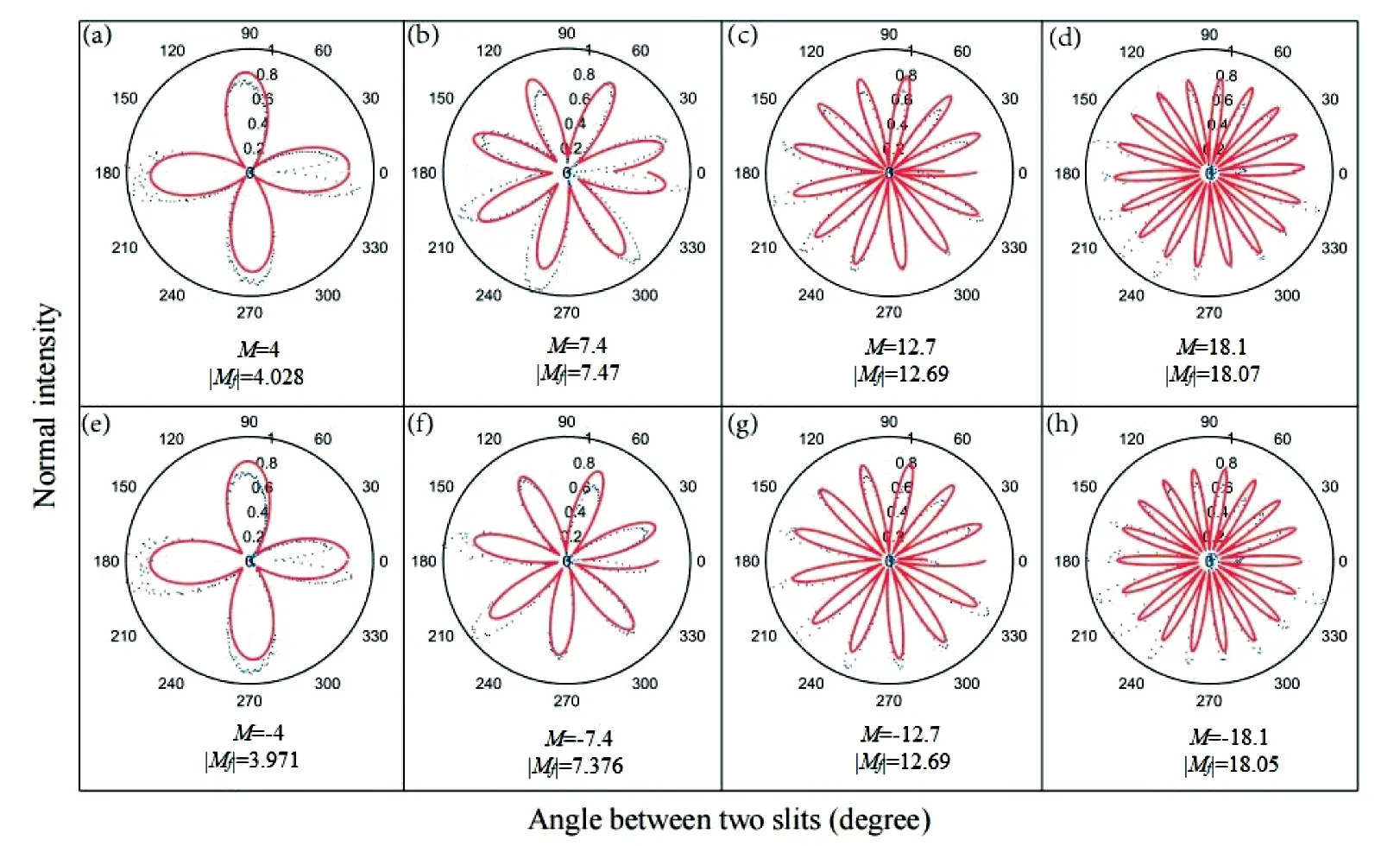
图12 极坐标下Δφ-I余弦关系曲线[51]

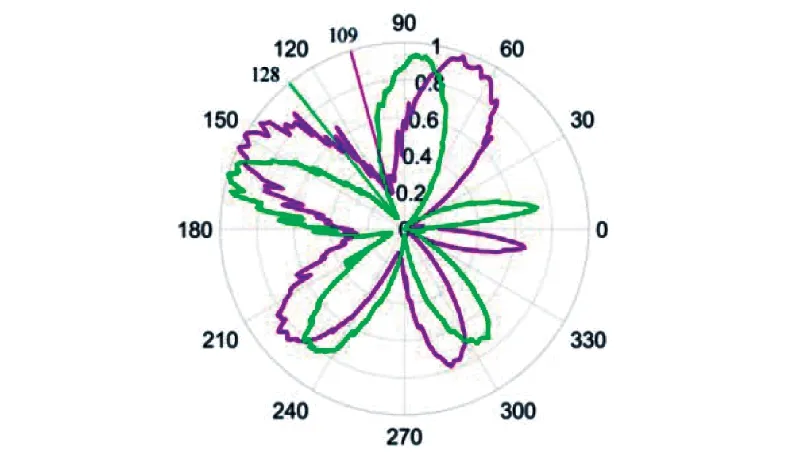
图13 当M=4.3时,对比余弦函数Δφ-I曲线(绿色曲线)与正弦函数Δφ-I曲线(粉色曲线)[51]

2.3 误差分析与讨论

由以上利用角双缝测量涡旋光束TC的实验结果可以看出,实验结果和理论结果相符,但不完全一样,误差主要来自角单缝的角宽度α、实验中角双缝旋转的步长、角双缝的中心与入射光束的中心不重合、实验中使用的非理想仪器以及背景杂散光的影响。角单缝的宽度α不能太宽也不能太窄,当宽度过大而不能对相位的2π变化进行采样时,会错过一些峰值,从而丢失一些关键信息;太窄会使得探测器收集的强度变少,背景光对Δφ-I曲线的周期变化影响更大。两个角单缝的旋转步长应足够小,以确保获得足够的实验数据,特别是对于高阶的涡旋光束。但这些误差的存在不影响Δφ-I曲线的周期和TC模量。另外,需要说明的是,对于多环涡旋光束,其干涉强度采集区域必须在原点附近。

此外,实验得到的Δφ-I曲线中有一个有趣的现象:在Δφ=2Nπ(N为整数)附近出现了分裂峰,如图8和图10所示,这可以通过考虑干涉和透射光强度来解释。干涉峰出现在2Nπ附近,角双缝的总透射光强度在2Nπ附近降低,这是由于角单缝的宽度和两个角单缝在2Nπ附近重叠,透射光能减小,因此,这两个机制的叠加导致了峰的分裂。在最极端的情况下,当角双缝间的夹角等于2Nπ时,即两个角单缝完全重合时,只有一个透射波,能量约等于另一个峰值强度的四分之一,因此,这个峰将一分为二。这一特征对于区分周期是非常有益的。分裂峰形成的原因如图14(a)所示,黑色曲线(分裂峰)是表示干涉强度分布的蓝色曲线与表示总透射强度的红色曲线叠加的结果。当在其中一个角双缝上加一个附加相位θ时,如图14(b)所示,其中黑色虚线表示Δφ=2Nπ(N为整数)的位置,绿色虚线表示当在其中一个角单缝上加附加相位时,蓝色实线的偏移量ΔΨ。由图14(b)可知,红色实线不变,但蓝色实线有偏移,而偏移方向由涡旋光束TC的正负决定,因此,黑色实线(直角坐标下的Δφ-I曲线)也发生了变化,特别是在2Nπ周围,分裂峰变得不对称,在实验中分裂缝甚至会消失,因为其中一个峰的强度太低,如图14所示。

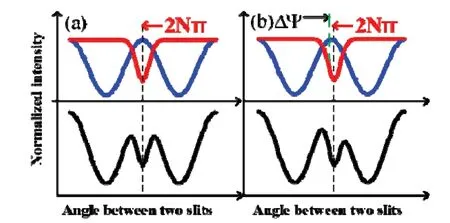
图14 分裂峰的说明图[49]

3 结论与展望

涡旋光束TC是表征涡旋光束的基本物理参量。由于涡旋光束的高维和光学涡旋特性,使得其在经典和量子信息领域展示出了巨大的应用潜力,已经引起广泛的关注,而根据TC区分不同涡旋光束的能力对基于涡旋光束的应用至关重要。本文针对LG光束、贝塞尔光束和POV光束,以整数阶涡旋光束与分数阶涡旋光束两类形式,对利用角双缝干涉精确测量任意涡旋光束TC模值和正负的方法予以阐述。当带有螺旋相位结构的涡旋光束经过角双缝,在远场产生的干涉图样依赖于两个角双缝间的相位差。因此,当扫描两个角双缝之间的夹角时,记录远场干涉图样中平行于角双缝角平分线方向处的光强,从Δφ-I曲线的周期性变化可以得到TC模值的信息。利用附加相位或Δφ-I正弦曲线,通过在极坐标下Δφ-I曲线的旋转方向确定TC的正负。这种简单有效的方法在不需要复杂的实验装置或复杂的干涉图样的情况下,清晰地揭示了涡旋光束的螺旋相位结构,为测量涡旋光束任意TC提供了一种方法。在后续工作中,可利用POV光束具有恒定环半径的优势,并考虑模式转换,将具有不同TC的普通涡旋光束转化为POV光束,采用固定尺寸集成检测设备,通过对POV光束TC进行测量,从而得出其它普通涡旋光束TC的信息。这些工作对基于不同空间模式编码的量子密钥分发、粒子操纵、光学积分、量子信息处理和基于涡旋光束的天文学研究等领域具有重要意义。