具有不连续初值的排斥趋化系统解的全局适定性

陈颂庄，彭红云

（广东工业大学 数学与统计学院，广东 广州 510520）

趋化性指的是细胞对环境中的某些化学物质做出反应而移动的趋势，即这些细胞会趋向或远离化学物质浓度较高的区域，前者称为吸引性趋化，后者称为排斥性趋化。很多学者对各种趋化模型进行了数学研究，例如，在20 世纪70 年代，Keller 等［1］提出了经典的趋化性模型，该模型描述了细胞黏菌对化学物质环腺苷酸（cAMP）的反应行为，Keller-Segel 模型的一般形式为

其中，D＞0 和ε≥0 分别表示细胞扩散系数和化学物质扩散系数，u 和c 分别表示细胞密度和化学物质浓度，ø（c）是描述信号检测机制的趋化敏感函数，g（u，c）是描述化学信号生长和降解的函数，而则表示化学信号的强度。当χ＞0 时趋化性是吸引的，而当χ＜0 时是排斥的。对于趋化函数ø，研究的三种类型分别为ø（v）=kv（线性律），ø（v）=klog（v）（对数律）和ø（v）=kvm/（1+vm）（受体定律），其中，k＞0 且m∈N。文献［2］将线性系统ø（v）=kv 和g（u，v）=u-v 命名为极小趋化模型。此外，文献［3］给出了该趋化模型相应的数学结果。而文献［4］研究了具有对数敏感性且g（u，v）=u-v 的模型（1）的稳态解，并在文献［5］中得到了全局解的存在性。本文研究在g（u，v）=uc-μc 和对数趋化函数ø（c）=k ln（c）下的一维模型

其中，μ＞0 表示化学物质降解速率的常数。该模型采用了Weber-Fechner 定律描述细胞趋化反应，并在文献［3，6-7，8］中给出了一些相应的生物学应用。随后，文献［9］给出了解的局部存在性和全局存在性。

其中初值条件和无穷远状态如下

当ε=0 时，系统（3）转化为以下的抛物-双曲方程

事实上，文献［10-13］首先建立了一维空间中系统（3）在ε≥0 时，行波解的存在性和非线性稳定性，其中波的强度可以任意大。此外，对于ε=0，文献［14］研究了一维空间中，系统（6）的Cauchy 问题在H2框架下经典解的整体存在性，进一步地，文献［15］研究了系统（6）具有不连续初值的Cauchy 问题的存在性、稳定性和正则性。而高维空间中系统（6）Cauchy 问题的一些研究可以参考文献［16］。在本文中，我们将考虑系统（3）在扩散系数ε＞0 时的初值问题

本文的目标是在初值（u0，v0）仅具有Lp-正则性（p≥1）条件下，证明弱解的全局存在性和稳定性。

1 主要结果说明

定理1 假设初值满足：u0-1∈L2（R）∩L4（R），v0∈L2（R），u0＞0，则Cauchy 问题（7）存在全局弱解（u，v）（x，t）满足

且有以下渐近收敛行为，当t→∞时

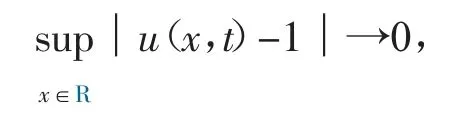
注1 初始值（u0，v0）（x）在定理1 初值条件下可能不连续，并且系统（7）中出现了类对流项［（v）2］x，这给能量估计带来了一些困难。为了证明定理1，我们构造光滑解序列逼近弱解。首先，对初始数据进行磨光，构造全局光滑解（uδ，vδ），得到一些（uδ，vδ）与δ 无关的能量估计，再取δ→0 的极限。

2 预备引理

引理1（Aubin-Lions-Simon）设X0，X，X1为三维Banach 空间，且满足X0⊂X⊂X1，X0紧嵌入X中，X 连续嵌入X1。对任意1≤p，q≤∞，记W=f∈Lp（［0，T］；X0）│∂t∈Lq（［0，T］；X1），有如下结论：

（1）如果p＜∞，则W 紧嵌入Lp（［0，T］；X），即W 在Lp（［0，T］；X）中是相对紧的；

（2）如果p=∞，q＞1，则W 紧嵌入C（［0，T］；X0）。

3 先验估计

接下来，通过引入一系列引理来证明具有如上所述初值的近似系统（10）的近似解满足一些与磨光参数δ 无关的全局先验估计。那么我们可以得到定理1 的近似解序列的δ-极限。在不引起混淆的情况下，将（uδ，vδ）记为（u，v）。

引理2 设（u，v）是方程组（7）的光滑解且满足定理1，那么存在一个不依赖于t 和δ 的常数C，使得

证明 将方程组（7）的第1 个方程与ln u 进行L2内积，将方程组（7）的第2 个方程与v 进行L2内积，并将结果相加，进而在［0，t］上进行分部积分，得到

以上不等式直接导出不等式（11），从而证明了引理2。

接下来，我们的目标是获得解关于时间的一致估计。

计算2×（15）-（16）可得

这里

由Cauchy-Schwarz 不等式可得

联立不等式（19），（20）和（21），可得

其中

这意味着

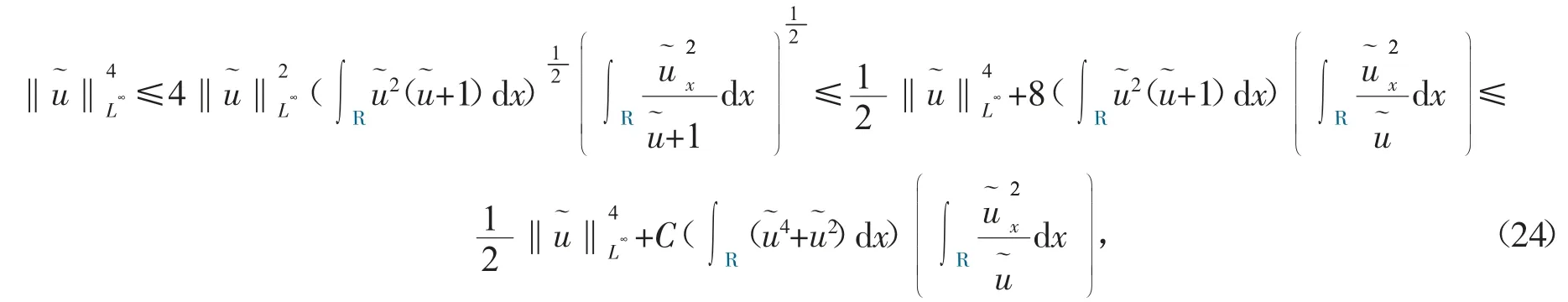
因此

将式（25）代入式（22），运用Gronwall 不等式可得式（14），引理3 证明完成。

为了得到最终的结果，还需要估计（u，v）的一阶导数。我们计划用磨光函数（uδ，vδ），通过令δ→0 逼近系统（7）的解（u，v），这要求（uδ，vδ）的一阶导数在与δ 无关的情况下一致收敛到（u，v）。在文献［12-14］中，可直接由H1估计得到该结果。然而，采用H1估计得到具有正则性低于H1（R）的初始值（u0，v0）问题的结果是不可能的。事实上，在L2（R）范数下，在H1估计过程中引入的项具有次有界［18］。因此，我们引用了一种巧妙的方法：利用加权函数σ=σ（t）=min｛1，t｝。值得注意的是，通过上述方法，我们只有在扩散系数ε 很小且不能被忽略的时候才能得到关于δ 的一致估计，却由于方程组（7）的第2 个双曲方程中存在v 的扩散项和以及v 只具有低正则性的初始值v0∈L2（R）∈L∞（R）），而不能得到关于δ 的一致估计。也就是说，我们只能得到以下uδ和εvδ的一阶导数的L2估计。

其中，σ=σ（t）=min｛1，t｝。

接下来，我们将估计式（23）右边的每一项。首先，由式（14）可知

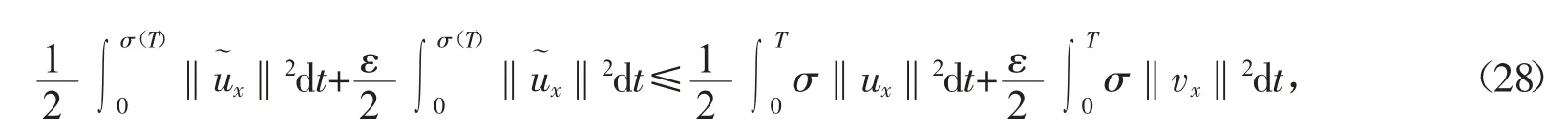
对于H1，由Sobolev 不等式≤2‖f‖‖fx‖，Cauchy-schwarz 不等式以及式（14）可得

类似地

这里取η＞0 足够小。把H1-H4的估计整合到式（29）可得

对于式（27）右边的最后两项，有

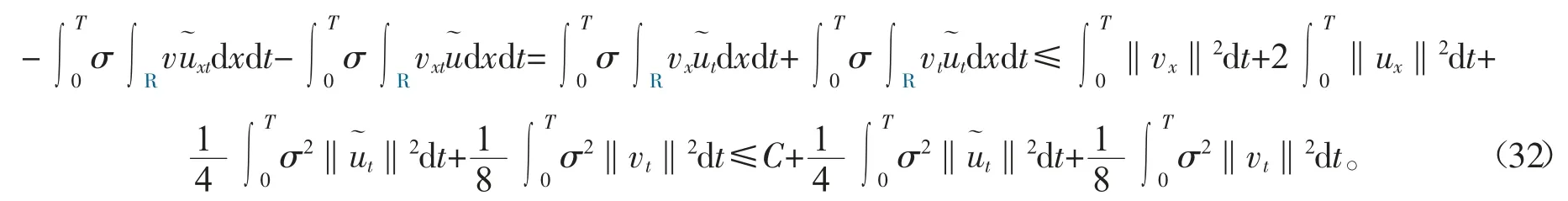
联立式（27）～（32）可得

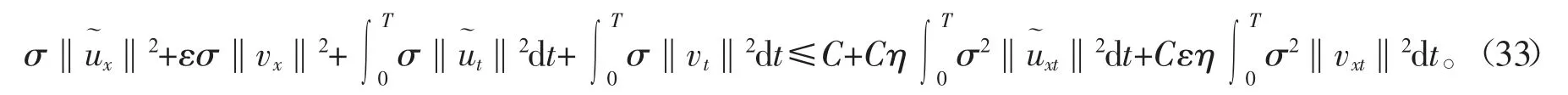
以下，通过对式（13）关于时间t 微分来估计式（32）右端项，这里有

由式（14）和式（33）可得

对于J3和J4，运用Sobolev 不等式和Cauchy-schwarz 不等式以及式（14）可得

将J1-J4插入式（35），有

由此，式（33）可简化为

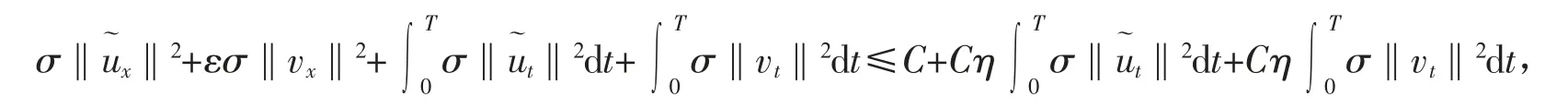
令η 足够小可直接得到

上式结合式（36）可得

整合式（37）和（38）直接得到式（26），引理4 得证。

证明 由式（14）和式（26）可得

其中，当t≥1 时，σ=1，导出

因此

以下，我们开始推导v 关于时间的一致上界。由引理4 和5 可知

其中，C（ε）独立于t。

4 定理1 的证明

根据引理3 和引理4，有

这表示

可以看出，当扩散系数ε＞0 时，上述结果与相同条件下ε=0 时的非扩散方程的结果一致。由式（42）和Aubin-Lions-Simon 引理（详见引理1），可以很自然地得到一个逼近序列（uδ，vδ），令δ→0，得到以下收敛结果

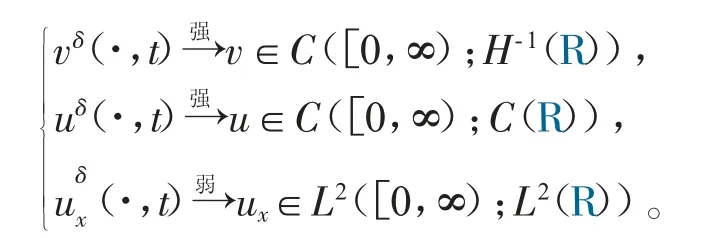
根据以上讨论过程，（u，v）确实是问题（7）的弱解，并且式（41）所示的上界成立。此外，我们必须在最后给出式（9）的证明来完成定理1 的证明。由引理4、引理5 和插值不等式可得

联立式（43）和（49），得到

结合v 的L2估计以及引理5，得到式（9）。