不同强度准则对预测岩石抗拉强度的适用性

2022-08-02杨宇

山西交通科技 2022年3期

杨宇

（1.山西省交通科技研发有限公司，山西太原 030032；2.山西省智慧交通研究院有限公司，山西太原 030032）

0 引言

岩石强度理论可以表征岩石在破坏条件下的应力状态和强度参数之间的关系，是岩土工程设计的理论基础[1]。目前，大部分强度准则是基于岩石三轴压缩试验提出，即考虑岩石的3个主应力，主要反映岩石的抗压和抗剪性能。但是，在一些工况下，需要岩石承受拉张应力，而且岩石抵抗拉应力的能力很差。例如，在地质构造稳定的山区进行硐室开挖，硐室上覆围岩层理水平，在硐室开挖后，顶端围岩在自重应力的作用下，会产生向两侧的拉应力，使得上覆岩层发生拉张断裂，对硐室稳定性造成影响。因此，在工程中，岩石抗拉强度是一个重要的力学参数。

目前，测试岩石抗拉强度的方法有很多，在现场主要通过点荷载试验测定抗拉强度，但是这种方法测得的结果离散型较大，只能粗略反映抗拉强度，若要得到更准确的抗拉强度，还需要借助室内力学试验进行测试。主要的室内测试方法有两种，直接拉伸试验和间接拉伸试验，直接拉伸试验可以精确地测得岩石抗拉强度，但是由于其试样制备困难，没有得到较广泛的使用。间接拉伸试验包括劈裂法和抗弯法，其中劈裂法应用最为广泛。但是劈裂法也存在很多问题，譬如加载方式、试样尺寸、计算方法等，国内外学者进行了相关的研究，这里不作赘述。

虽然关于岩石抗拉强度的研究逐渐深入，但是还存在诸多问题，岩石破裂形态与抗拉强度的关系尚不明确，间接拉伸法计算岩石抗拉强度中的误差分析，考虑岩石各向异性的抗拉强度计算等。基于此，本文结合前人研究成果，对比不同破裂形态，对传统抗拉强度计算公式进行了改进。此外，分别利用几种不同强度准则预测了岩石的抗拉强度，通过与试验数据进行对比，判断了强度准则预测抗拉强度的适用性。研究结果可以为抗拉强度计算和预测提供一定的科学依据。

1 几种强度准则

1.1 直线型Mohr-Coulomb准则

Mohr-Coulomb强度准则建立于1900年，直至现在仍然是工程设计的主要依据。该准则是基于岩土材料的剪切破坏提出的，没有考虑中间主应力的影响，利用莫尔圆来表示应力状态，其表达式为[2]：

式中：τ为剪应力；c为黏聚力；σ为正应力；φ为内摩擦角。

由式（1）可以推导得到主应力的表达式：

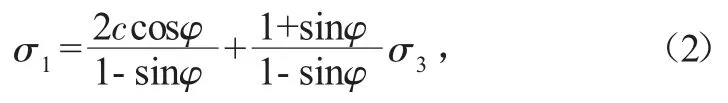
式中：σ1和σ3分别表示最大主应力和最小主应力。

令σ1=0，σ3=-σt，可以得到单轴抗拉强度σt的表达式：

1.2 抛物线型Mohr-Coulomb准则

通过大量试验发现，岩土材料的包络线并非是一条直线，因此佘成学等人[3]提出了双参数的抛物线型M-C准则，具体表达式为：

其中，a、b可以表示为：

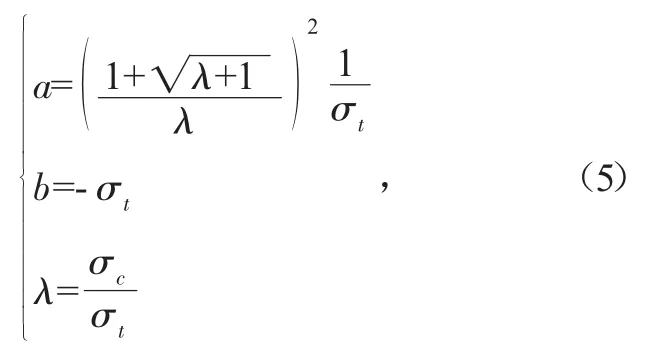
式中：σc为单轴抗压强度。

式（5）可以用主应力表示为：

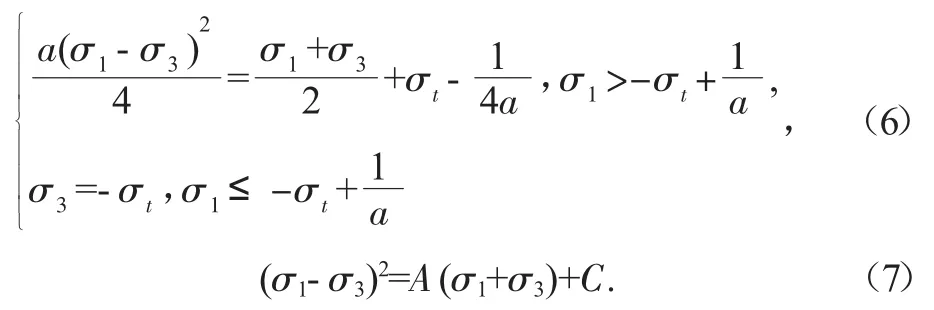
A和C可以通过线性回归得到，由此可以计算单轴抗拉强度：

1.3 Griffith强度准则

Griffith强度准则最早出现在材料力学中，用于描述裂纹尖端效应，后来被引入岩土工程中，来描述岩体中微裂隙的扩展。Griffith认为，引起裂纹扩展的应力为拉应力，因此提出了关于拉应力的强度准则[4]：

利用式（9）便可以计算出岩土材料的抗拉强度。

1.4 Hoek-Brown准则

Hoek-Brown准则是在大量试验基础上提出的一种经验准则，狭义表达式为[5]：

式中：m为试验参数。

令σ1=0，σ3=-σt，可以得到单轴抗拉强度的表达式：

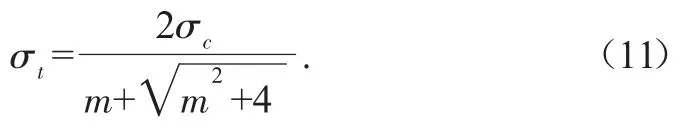
1.5 Lade-Duncan准则

Lade依据于砂土的真三轴试验结果，在1975年提出Lade-Duncan准则[6]，考虑了中间主应力的影响，并且在1984年进行了进一步修正，使其适用于更多的岩土材料[7]。这里用1984年修正后的L-D准则表达式进行计算：

式中：Pa为一个标准大气压；η1、m为材料参数；I1、I3分别为第一、三应力张量不变量。

当材料中存在拉应力时，需要加上I1+3αPa，αPa为材料抗拉强度。α为材料参数。通过进行推导得到：

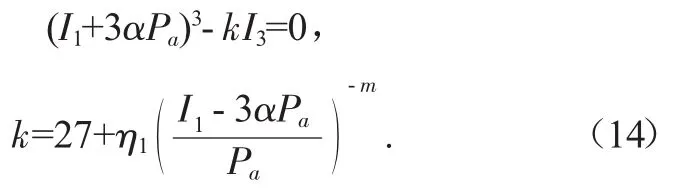
通过进行数值回归，可以得到材料的抗拉强度。

2 抗拉强度计算

一般计算岩石的抗拉强度有两种方法，分别为直接拉伸和间接拉伸，由于直接拉伸试验所需的试样很难制作，因此目前大多工程和研究均采用间接拉伸法，常用的方法就是巴西劈裂试验。根据国际岩石力学学会（ISRM）所提到的抗拉强度试验与计算方法[8]，依据图1中的几何关系，得到了弹性力学平面应变问题解析。式（15）表示了A点的应力状态。

图1 圆盘应力状态

在圆心处O点处，θ1=θ2，r1=r2。所以可以将式（15）简化为：

式中，由于y方向的力是x方向的3倍，所以认为σx=σt。即岩石所受的拉应力为圆心处沿x方向的应力。

3 对比与分析

3.1 抗拉强度计算公式修正

ISRM建议的抗拉强度计算方法将圆盘中心点的水平应力作为抗拉强度，但是大量巴西劈裂试验现象表明，很多试验并不是中心起裂，还有其他形态的破裂方式，如图2所示。并且研究发现，非中心起裂的破坏模式多见于层理发育的沉积岩中，层理岩石的横观各向同性特征导致了偏心破裂。此时用式（16）计算得到的抗拉强度与实际有偏差，该情况下抗拉强度的误差有多大？是否在可接受范围？基于此，考虑非中心破裂形式，对式（16）进行了修正。

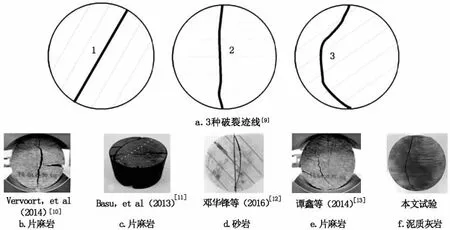
图2 巴西劈裂试验的破裂迹线

基于此，考虑到非圆心破坏的破裂面形态，利用几何数学对破坏迹线进行了分析。假设破裂面为一条半径为r，弦长为D，圆心角为α的标准圆弧l，如图3所示。图中a为弧顶与圆心的距离，由此可以通过图中的几何关系得到l。当破裂面沿着直径D破坏，此时l=D'。

图3 破裂面的几何关系图

由此可以得到弧长，再通过式（18）：

可以得到裂纹为弧线条件下岩石的抗拉强度σt：

式（19）中，a、P可通过试验直接得到。

以图2中提到的4个非中心破裂的试验结果为对象，分别利用式（16）和式（19）计算得到了抗拉强度（表1）。

从表1中可以看出，非中心起裂的抗拉强度要略低于中心点的抗拉强度，并且偏心距越大，强度降低越多。劈裂法测得的是圆心位置的抗拉强度，但是在出现非中心起裂时，实际抗拉强度应分布在破裂迹线上。计算结果表明，在巴西劈裂试验中，按照传统方法计算非中心起裂试样的抗拉强度，其结果偏高。由此可得到一组计算抗拉强度的公式：

表1 修正前后试样抗拉强度对比

黄耀光等人（2015）[14]研究表明圆盘上的水平应力偏离中心点越远，其值越小（图4），本文计算结果符合这一规律。

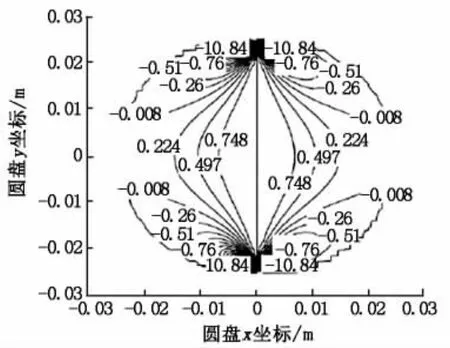
图4 巴西圆盘无量纲水平应力

3.2 强度准则适用性分析

为验证以上强度准则的适用性，以太行山奥陶系泥质灰岩为对象，分别开展了三轴压缩和巴西劈裂试验，试验结果列于表2。

表2 奥陶系泥质灰岩三轴试验结果

结合张磊等人[15]以及本文的试验结果，分别利用上述5种强度准则进行计算分析，得到了不同强度准则对比下的应力关系图，如图5所示。

图5 应力关系曲线

通过将试验数据与计算结果进行误差对比，可以将拟合情况定量化，利用式（21）进行误差分析：

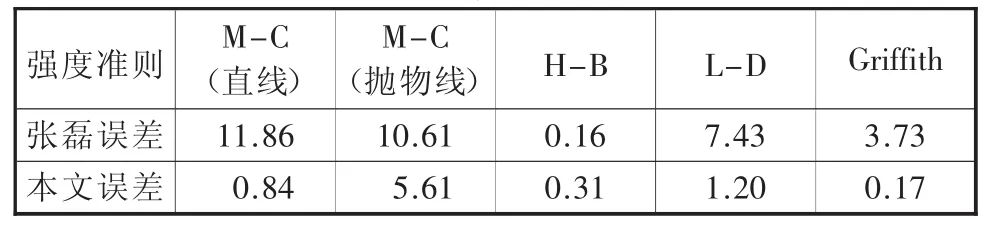
表3 误差分析对比结果

表3中可以看出，在高围压条件下，H-B准则是最接近试验数据的，该结果与刘运思等人[16]的研究结果相符合。其次是Griffith准则，而两个M-C准则的拟合程度较差，相比于直线型M-C准则，抛物线型的更接近实际数据。由于H-B准则是基于大量试验数据的经验准则，并且其中有拟合参数，在本算例中该拟合参数是通过试验数据拟合得到，所以最终的计算结果与实际最为接近。Griffith准则是针对于抗拉强度提出的强度准则，因此相比于其他强度准则，在计算抗拉强度时更为有效。而L-D准则与其他准则最大的区别是考虑了中间主应力的影响，为三维应力空间状态，在本文的计算中，以假三轴状态为背景，认为中间主应力与最小主应力相等，因此其最终的计算结果会有较大的偏差。而M-C准则，作为最早的强度准则，更多地考虑岩土材料的剪切破坏，不适用于计算拉张破坏，而Griffith准则更适用于低围压条件。

Griffith强度准则是基于裂隙扩展提出的岩石抗拉准则，其中不考虑剪切行为，岩石裂隙发育贯通是造成岩石受拉破坏的本质因素，这个结果解释了地表出露高陡灰岩边坡竖直拉张节理发育现象。而H-B准则是岩石抗剪强度准则，拉张破坏本质上是剪切破坏的一种特殊情况，没有考虑裂缝的扩展。在高围压下，岩石以剪切破坏为主，主要发生塑性变形。因此深部岩体潜在剪切面通常是连续的，并且具有较好的延伸性，常发生大型断裂、断层、深层滑动等。而浅表层岩体多出现短小的节理，以竖直方向为主，将岩体切割成大量块体，常形成崩塌落石、楔形体滑动等。