基于影响线轻荷载试验的桥梁承载力评估方法研究*

王珊珊，张荣凤，亓兴军，赵 奇

(1.山东高速集团有限公司，山东 济南 250098； 2.山东建筑大学交通工程学院，山东 济南 250101)

0 引言

桥梁运营期间，受到自然灾害或人为等因素影响，导致材料老化、结构受损，对桥梁的安全性和承载力产生威胁[1-2]。我国颁布了JTG/T J21-01—2015《公路桥梁荷载试验规程》，美国、加拿大等国颁布了新的桥梁承载力使用规范，规范中给出的评估模型可用来评价各种类型的桥梁[3-5]。由此可见，桥梁承载力评估是国内外桥梁界关注的问题，而桥梁荷载试验是公认的评价桥梁承载力的有效方法，但传统的荷载试验具有以下缺点：编制试验方案时为了满足加载效率，需不断调整加载车辆自重及位置；试验过程中需封闭交通，现场也需工程师指挥调配加载车，整个试验流程操作繁琐、耗费大量人力物力。

常丁通过分析校验系数，得出其可由结构的抗弯刚度表示，混凝土结构的挠度随外荷载变化，传统荷载试验采用逐级加载方式，这是一个外荷载变化的过程，因此每一级加载工况下，桥梁挠度变化，校验系数也变化；通过对分级过程中的校验系数进行研究，找到分级加载下校验系数的相关性，便可由轻荷载下校验系数计算重荷载下的校验系数，因此研究了基于轻荷载试验的梁桥承载力快速评定方法。轻荷载试验是指由少量试验车辆进行的试验，重荷载试验是指满足试验规程中荷载效率 0.85～1.05 的试验，通过校验系数分析理论，建立不同荷载效率下结构校验系数的函数关系，给出由轻荷载校验系数得到重荷载校验系数的计算方法[6]。林迪南根据常丁的试验方法，对桥梁进行了快速评估，并将校验系数差值范围及相对差值-对应荷载效率回归方程称为“常丁模型”[7]。袁治和杜晶采用轻荷载试验研究了荷载分布系数，为桥梁横向联系损伤提供指导[8-9]。陈彦坤根据不同桥型组配出桥梁检测适合的仪器方案，再基于轻荷载试验完成桥梁承载力的快速评定，提高了检测效率[10]。轻荷载试验以其快速完成荷载试验、提高工作效率、节省资源等优点，成为快速评估桥梁承载力新的研究方向。

准静力影响线可通过缓慢匀速跑车的方式来获取[11]，单辆跑车沿着指定路线缓慢驶过桥面便可完成试验，获得数据量大且稳定，相对于传统荷载试验来说，影响线跑车试验快速便捷，单辆跑车可作为轻荷载加载，根据“常丁模型”，可用于新桥评定或主梁处于弹性范围内的旧桥承载力评估。本文以影响线跑车作为轻荷载，根据“常丁模型”的计算方法，对某高速公路的佟家庄大桥承载力进行快速评估。

1 轻荷载试验方法

在编制桥梁荷载试验方案时，往往要根据控制荷载进行逐级加载，这使得在试验中因逐级加载而耗费大量时间。因此，从减少荷载试验车辆数量着手，常丁提出基于轻荷载的加载方式[6]。借鉴“常丁模型”轻重荷载校验系数转变方法，本文基于影响线轻荷载试验方法的思路为：利用准静力影响线测试车作为轻荷载加载，采集1辆测试车加载工况下桥梁的挠度和应变影响线数据；建立桥梁有限元模型，计算轻荷载下静载试验的加载效率与校验系数，利用“常丁模型”计算转变为满足加载效率 0.85～1.05 的传统荷载试验校验系数，结合现行规范对新桥或仍处于线弹性范围内旧桥承载力进行快速评估。

校验系数在桥梁承载力评定中是一个重要指标，其数学公式为：

(1)

式中：Se为试验荷载作用下测量的结构弹性挠度(或应变)值；Ss为试验荷载作用下计算的结构挠度(或应变)值。

由文献[6]可知，将材料力学中应变的计算公式 (2)代入式(1)，得到校验系数由刚度定义的表达式(3)：

(2)

(3)

式中：M为梁上荷载在某一截面处引起的弯矩；y为该点到截面中性轴的距离；Se为试验荷载作用下测量的结构弹性应变值；Ss为试验荷载作用下理论计算结构最大应变值；EI为梁的弯曲刚度；EsIs为理论抗弯刚度；EeIe为实测应变对应抗弯刚度。

由式(2)与式(3)可知，结构的应变校验系数从形式上可由应变值转变为刚度值，其可由结构的理论计算抗弯刚度与实测应变对应抗弯刚度的比值表示。

如图1所示，某一集中力作用在简支梁上，由结构力学得到简支梁的挠曲方程式(4)：

图1 受集中力作用的简支梁

(4)

将式(4)代入式(1)，得到挠度校验系数也由刚度定义，其计算公式如下：

(5)

挠度校验系数从形式上看可由应变值转变为刚度值，同理，挠度校验系数也可由理论抗弯刚度与实测挠度对应抗弯刚度的比值定义。因此，校验系数与结构的刚度有关，若结构处于线弹性范围内，校验系数为常数，与加载车自重和位置无关；但对桥梁进行荷载试验时，分级加载是外荷载递增的过程，实际荷载效率也随之变化，于是得到：每级荷载加载工况下，加载效率与校验系数间存在一定的函数关系；重荷载与轻荷载下校验系数间也存在一定的函数关系，如此通过轻荷载的加载效率便可求得重荷载下的结构校验系数，结合规范便可实现对桥梁承载力的评估。文献[6]通过对103座中小跨径桥梁(预应力混凝土桥66座，钢筋混凝土桥37座)荷载试验的分级加载数据统计分析，得出钢筋混凝土梁桥的校验系数差值范围。在分析校验系数的关系中，<0.85的荷载效率分为5个档次范围，分别为0.75～0.84，0.65～0.74，0.55～0.64，0.45～0.54，0.3～0.44。以荷载效率作为分类标准，采用做差值的方法分析，对重荷载与所划分的轻荷载下的校验系数进行计算，得到如下公式：

Δa=ζ-ζn

(6)

(7)

式中：Δa为绝对差值；ζ为在荷载效率0.85～1.05内的应变(或挠度)校验系数；ζn为在<0.85的5个荷载效率范围内的应变(或挠度)校验系数，n=1～5；Δr为相对差值。

利用四分位法对所统计桥梁的各荷载效率下对应的结构应变(或挠度)校验系数差值进行分析，得到校验系数差值范围，建立相对差值与其相对应的荷载效率间的回归方程。联合差值范围与式(6)和式(7)计算可得到重荷载效率下的校验系数，其中钢筋混凝土梁桥的Δr-η回归方程如表1，2所示[6]。

表1 钢筋混凝土梁桥应变校验系数差值范围

表2 钢筋混凝土梁桥挠度校验系数差值范围

2 基于影响线跑车加载的桥梁承载力评估

2.1 工程概况

某高速公路的佟家庄大桥全长270.66m，跨径组合为13×20m，桥面总宽度为2×11.2m，横向布置为 0.5m 护栏+10.25m净宽+1.5m分隔带+10.25m净宽+0.5m护栏。上部结构为C40简支钢筋混凝土 T形梁，下部结构为肋板台、柱式墩、桩基础。该桥于1993年建成通车，设计荷载等级为汽-20、挂-100。现桥面铺装为13cm厚C40混凝土铺装层+7cm厚沥青铺装层。该桥整体外观及桥梁横断面、立面如图2～4所示。

图2 佟家庄大桥整体外观

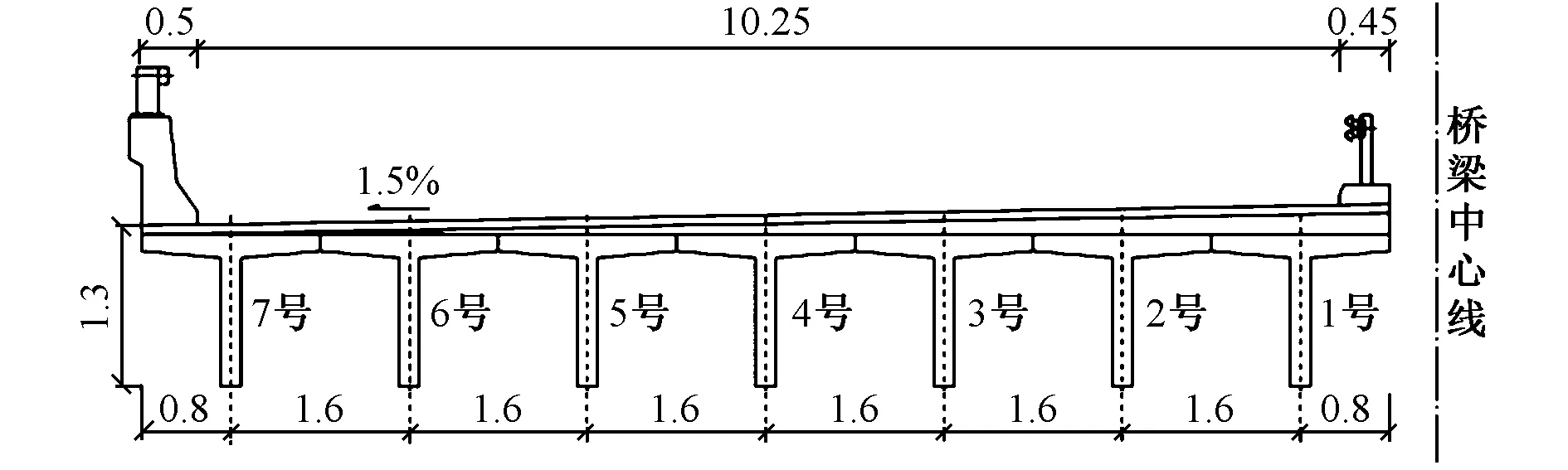
图3 桥梁横断面(单位：m)

图4 5×20m T梁连接示意(单位：m)

2.2 试验工况

影响线测试分为2个工况：②工况1 挠度和应变影响线测试，测试车车道距离桥梁内侧2.4m，测试车以<5km/h的速度匀速通过桥梁，连续采集记录数据；②工况2 挠度和应变影响线测试，测试车车道距离桥梁内侧4.2m，测试车以<5km/h的速度匀速通过桥梁，连续采集记录数据。其中，测试车辆轴距分别为1.45，4.10m，轴重分别为13.46，13.46，9.94t，影响线测试工况及跨中截面测点布置如图5所示。

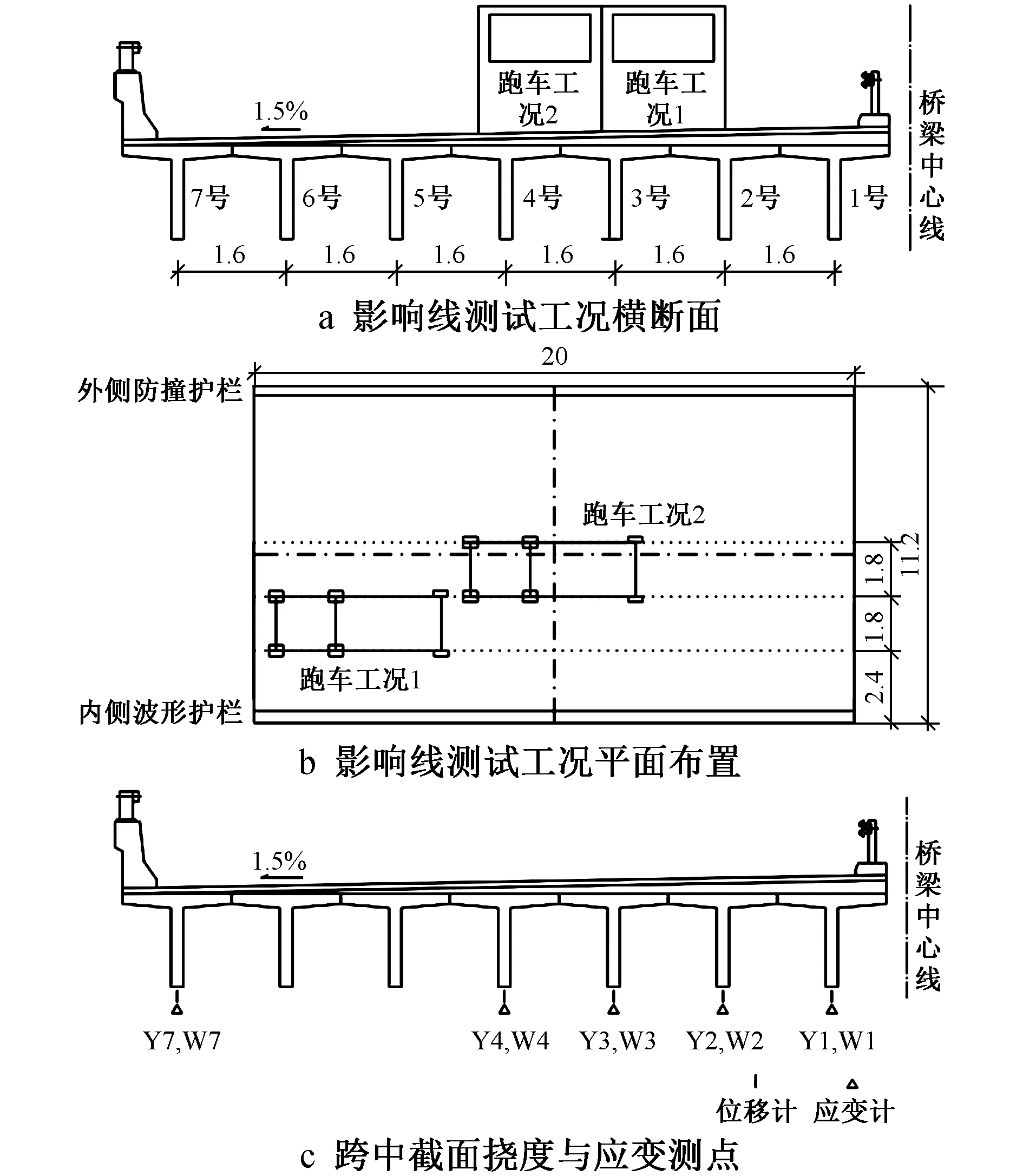
图5 影响线测试工况及测点布置(单位：m)

2.3 承载力评估

利用轻荷载试验进行桥梁承载力评定，首先计算轻荷载加载效率。利用ANSYS有限元软件建立试验桥梁有限元模型，主梁采用shell63单元，实横梁采用beam4单元，变厚度混凝土铺装采用solid65单元，厚度从桥面外侧0.08m渐变至桥梁内侧0.248m，形成1.5%横坡，支座采用combin单元模拟，竖向刚度为1×1010N/m；通过耦合模拟横向连接；支座设置在距梁端0.25m处，采用简支约束。施加挂-100设计荷载，计算跨中截面挠度效应值，施加设计荷载的有限元计算模型如图6所示，挠度变形如图7所示。

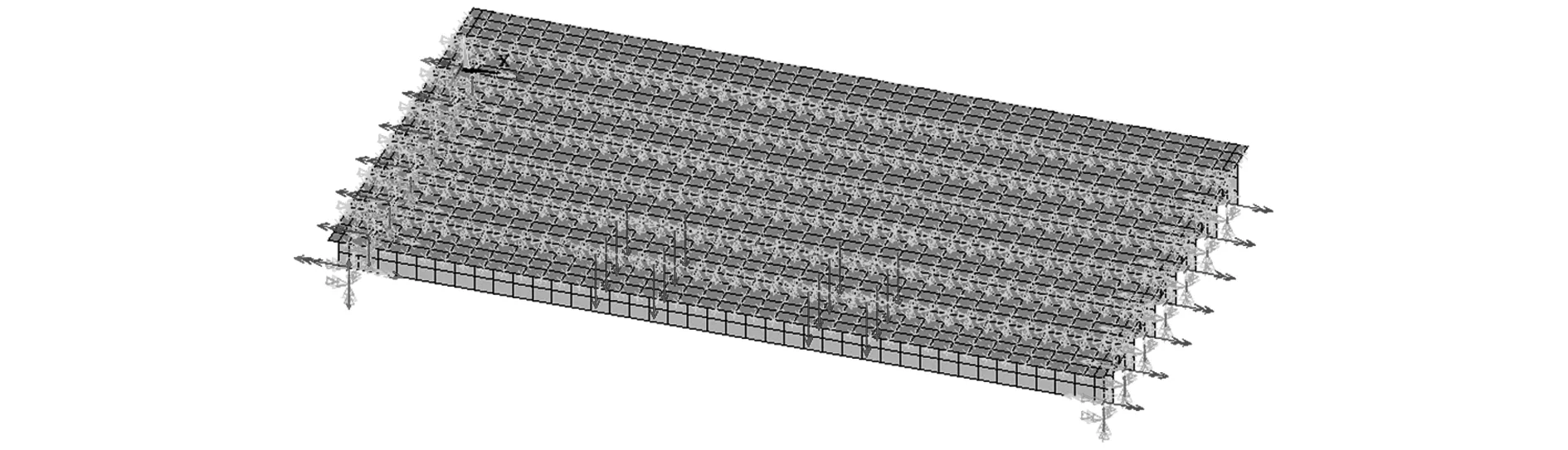
图6 设计荷载计算模型

图7 设计荷载作用下挠度变形

影响线测试车加载后提取各测点挠度值，根据荷载试验规程，利用跨中整体截面的挠度值计算加载效率，得到影响线测试工况1，2的荷载效率，如表3所示。

表3 轻荷载试验荷载效率系数

由表3可知，工况1，2的挠度轻荷载效率在0.3～0.84，可采用Δr-η回归方程进行计算。采用ANSYS有限元软件计算影响线测试工况1，2的理论计算值，根据跨中截面的1～4号和7号测点的理论值与实测值，计算基于轻荷载的应变校验系数和挠度校验系数，结果如表4，5所示。

表4 轻荷载试验下跨中截面应变校验系数

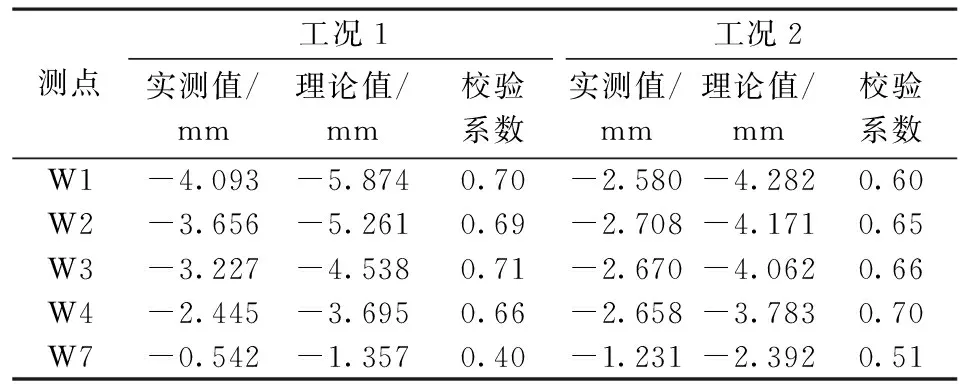
表5 轻荷载试验下跨中截面挠度校验系数

由表4，5可知，工况1的轻荷载应变校验系数分布范围为0.53～0.98，平均值为0.80，轻荷载挠度校验系数分布范围为0.40～0.71，平均值为0.63；工况2的轻荷载应变校验系数分布范围为0.72～1.02，平均值为0.85，轻荷载挠度校验系数分布范围为0.51～0.70，平均值为0.62。根据轻荷载加载效率及校验系数回归方程，将2个轻荷载效率下的校验系数转变为满足荷载效率0.85～1.05下的校验系数，转变后2个工况的应变校验系数与挠度校验系数数据如表6所示。

表6 轻荷载校验系数转变为重荷载校验系数数据

统计轻荷载与重荷载校验系数各自的分布范围，结果如表7，8所示。

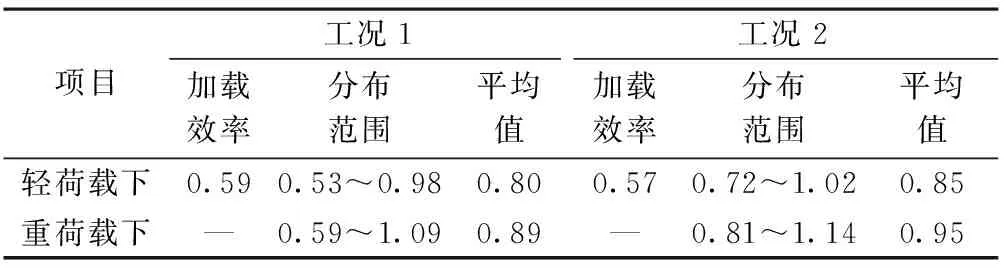
表7 应变校验系数分布范围

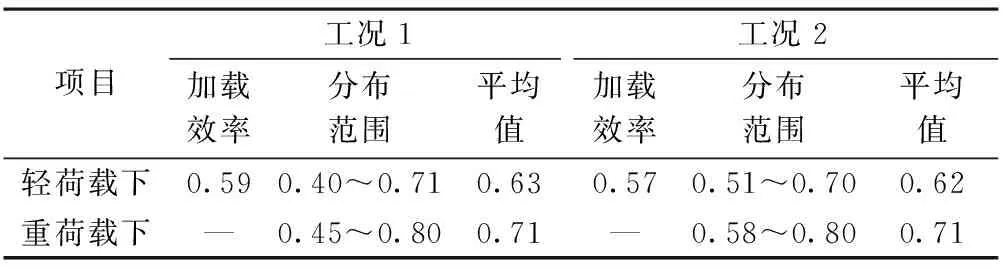
表8 挠度校验系数分布范围

由表6～8可知，由轻荷载下校验系数转变为重荷载下校验系数后，各测点的挠度校验系数均<1，说明桥梁整体结构处于弹性工作状态，但3，4号测点应变校验系数存在>1的情况，表明该桥的承载力不满足设计要求。

3 影响线轻荷载试验与传统试验对比

3.1 传统荷载试验

选择佟家庄大桥第7跨跨中截面作为控制截面，7片梁底分别布置挠度传感器及应变传感器，所有传感器布置如图8所示。

图8 跨中截面测点传感器布置

荷载试验选择3辆三轴车作为加载车，各加载车的车辆信息如表9所示，荷载试验加载车平面布置及现场试验如图9所示。

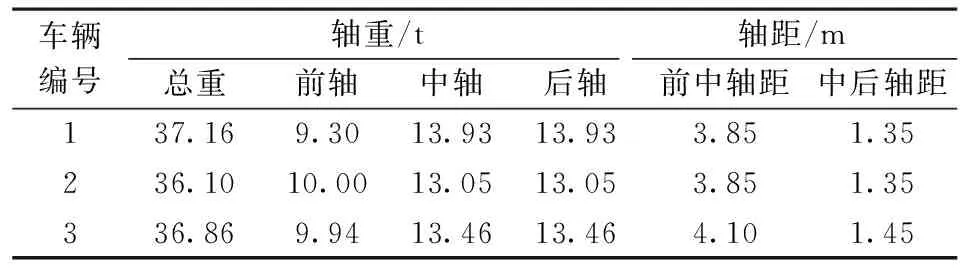
表9 加载车辆尺寸及轴重

图9 加载车辆平面布置(单位：m)

在试验荷载作用下，试验跨截面实测应变、挠度数据如表10，11所示。

表10 跨中截面实测应变

表11 跨中截面实测挠度

由表10，11可知，跨中截面2号测点应变校验系数与挠度校验系数均>1，3～7号测点应变校验系数分布范围为0.71～0.99，挠度校验系数分布范围为0.47～0.70，相对残余应变最大值为3.88%，相对残余挠度最大值为8.46%；荷载试验下最大残余系数<20%， 表明桥梁结构处于弹性工作状态，2号测点应变校验系数与挠度校验系数均>1，不满足承载力评定规程中静力荷载试验校验系数<1的要求，表明桥梁实际承载力不满足设计要求。

3.2 两种试验结果对比

现场试验时，传统荷载试验加载车辆位于桥梁外侧，影响线测试路径靠近桥梁内侧，且影响线测试工况仅采集1～4号与7号梁底数据，并未采集5，6号梁底试验数据，因此，无法将轻荷载转变为重荷载得到的校验系数与传统荷载计算的校验系数针对每片梁一一对应比较，故将2种试验方法得到的校验系数的分布范围与平均值做统计对比，结果如表12所示。

由表12可知，试验桥梁采用传统荷载试验方法得到的校验系数和轻荷载试验方法计算的校验系数相比，应变校验系数平均值误差分别为1.14%，7.95%；挠度校验系数平均值误差均为5.97%，各校验系数平均值误差均在10%以内，说明基于影响线轻荷载加载的试验方法得到的校验系数相对于传统试验得到的校验系数的误差较小，可用于桥梁的承载力快速评定。

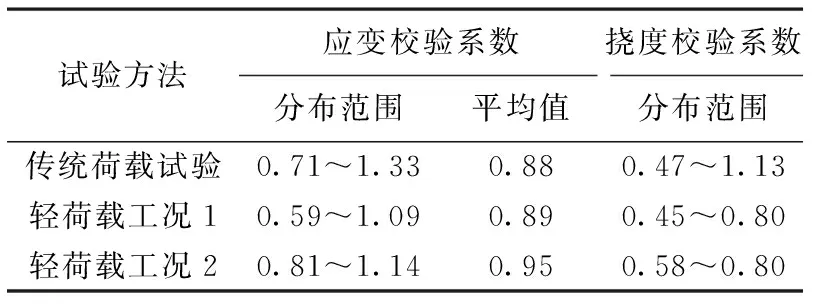
表12 传统荷载试验与轻荷载试验校验系数对比

4 结语

利用影响线轻荷载试验对桥梁进行承载力快速评估，得到以下结论。

1)利用影响线轻荷载对新桥或仍处于线弹性范围内旧桥承载力进行评估，评估结果和传统荷载试验评估结果相比误差较小，和传统荷载试验相比，应变校验系数和挠度校验系数的平均值误差均≤10%， 表明基于影响线的轻荷载试验方法具有高效性与可行性，可实现桥梁承载力快速评估。

2)轻荷载试验利用更少的测试车辆完成试验，且花费较少试验时间，相比于传统荷载试验节省人力物力，降低试验成本。

3)基于影响线的轻荷载试验，仅需1辆测试车便可完成荷载加载及试验数据采集，且准静力影响线包含更多的桥梁静力信息，结构响应数据精准可靠，评估结果准确可靠。