基于智能算法的汽车内部噪声主动控制方法

0 引言

车辆在城市中越来越重要，但是汽车的内部噪声是由空气和固体结构振动引发的声响，大部分噪音都主要是较为低频的声响。之前一直善用的车内噪声控制方法，一般都采用在噪声传播过程中的隔振、隔声、消声、吸声等降噪措施，这些措施用来抑制高频噪声的效果很好，可是对于低频噪声的控制展现效果便较为一般。按照现在的情况来看，自适应主动噪声控制在低频降噪领域较为重视，一直进行着广泛的理论研究，并将其加以工程上的应用，已被证实是一种优秀的汽车内部降噪方法。目前，自适应算法的研究是噪声主动控制技术的核心。在自适应有源噪声控制方法中，有一种算法相对来说较为方便，计算量小且稳定性高的LMS算法来计算最小均方值。LMS算法简单有效，能够跟踪噪音，并适应所处的噪音环境。此算法的最终目标是适应多个传感器中最小误差处的声量值，以此来推断传声器周围的降噪点。然而，智能计算程序存在不能考虑收敛速度和稳态误差的固有缺陷。在保证算法收敛性的前提下，步长越大越可以提高算法的收敛速度，同时也会促使稳态误差上升。相反，如果减小步长，收敛速度也会随之减小，造成稳态误差的降低。想要解决智能算法中存在的问题,有必要对汽车车内噪声的鲁棒性分析的LMS智能算法是最广泛使用的一种算法,这种计算方式可以收敛的更全面，直接代替传统算法,成为基于智能算法的汽车内部噪声主动控制的最有效方式。

1 汽车内部噪声自适应陷波控制

1.1 汽车内部噪声采集

GB/T18697_2002为声学车辆车内噪声测量的国家标准方法，以此来采集车辆内部制动噪声的数据最为准确。其原理图见图1。

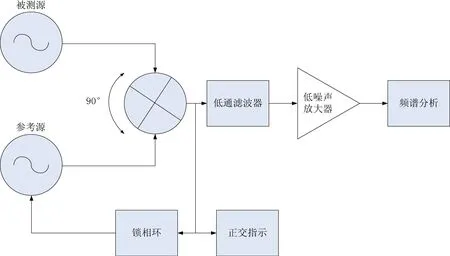
采集噪声的车载设备为PULSE噪声采集分析设备，属于声音采集软件，系统软件与硬件设备齐全。采集的车辆工况大概在60千米每小时的紧急制动，直至车辆静止。收集到的信号是汽车前排驾驶员耳朵里的噪音。对于语音采集，可以检索现有的WAV文件进行语音读取。电路原理图见图2。

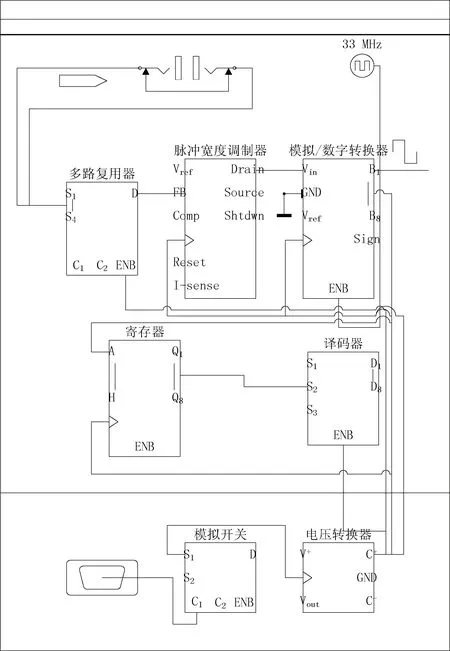
采样值置于向量中，采样频率表示采样数。在MATLAB中放置声音文件，或者直接将采集到的声音信号上传给MATLAB，以此创建一个文件夹来保存音频数据，这个文件夹内涵盖了采样所需时间以及录制好的音频内容。

采集汽车内部的噪音时，实际乘坐在汽车中人员并没有感觉乘坐舒适，他们的反馈大多数都是如此的，甚至还觉得比较单调，制动听觉效果比较一般。根据一些测试和判断可以看出，汽车内部的干扰噪声为低频噪音，其能量幅值在频率较低的地方波动较大，占据了一定的主导位置。对于声音的回放，所有记录到的刹车声音也都属于录音内容的一部分。用频率为44500 Hz的Matlab软件对格式文件进行转换，对每辆车选取质量最好的噪声信号，从而对车内制动噪声的时域和频域进行分析。在Matlab环境中,对信号噪声进行分析，根据快速傅里叶变换以及时域信息得到光谱显示,车辆的噪声在一般情况下都属于低频状态，整个频谱的噪声能量集中在低频率，紧急制动大约为400赫兹左右,处在高频以及中频的噪音分量幅值很小，在乘车的实际体验中，对于噪声的感受大致是一致的。汽车内部的噪声信号在大多数情况下都是时变信号，在短时间内被傅里叶转化，详细分析可以制动的信号时频能量信息分布。因为绝大多数散落分布的信号能量都不超过400赫兹，所以汽车内部噪声采集只分析噪声的低频区间。

由图4和表3可知，① 弹性阶段各曲线变化明显，随着钢管厚度增大初始刚度逐渐增大，斜率增大，承载力明显提高，承载力与挠度成线性关系。在此阶段，圆钢管的壁厚变化对柱子性能影响较小；② 弹塑性阶段中曲线上升斜率随钢管厚度增加而提高，当壁厚大于8 mm时出现明显的平缓段，出现一定的上升坡度。增加壁厚极限承载力也越来越大，体现了钢管的环箍作用；③ 塑性阶段，壁厚越小，在到达极限承载力之后的下降段越明显，坡度越大，易发生脆性破坏，下降段越长，变形能力越好；壁厚越大，下降段越平缓，延性越好，柱子的抗变形能力越好。

1.2 噪音的自适应波动处理

第三，企业审计人员凭借自己的专业知识和工作经验无法准确界定被审计企业的经济责任时，要咨询这方面的权威专家，这样可以提高企业经济责任审计结果的准确性与合理性。

术后有5例患者发生并发症，发生率为1.25%（5/400）。对患者的护理满意度进行调查，其中218例患者满意，163例患者一般满意，19例患者不满意，护理满意度为95.25%（381/400）。

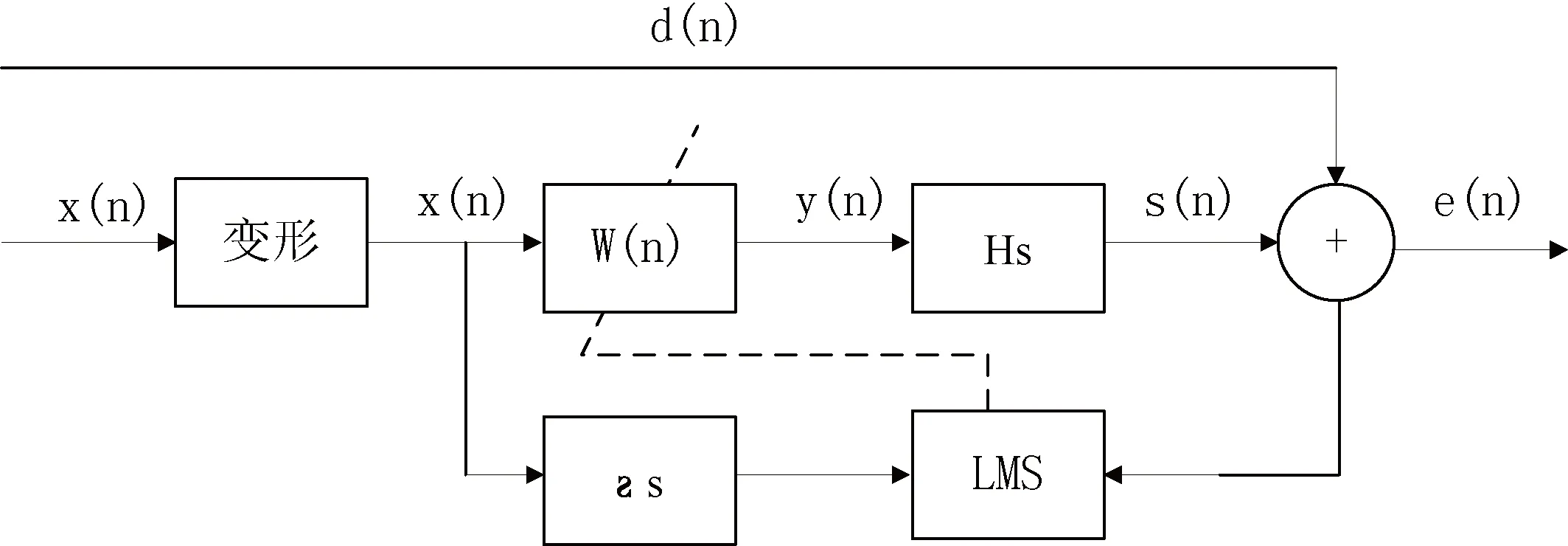
在智能算法的基础上，对车辆内部噪声样本数据进行分析，采用变步长LMS算法更新自适应陷波器中的权重向量，并建立车辆的主动噪声控制，其线性滤波器的基本结构如图4所示。

当噪声陷波固定时，若是希望在算法中得到快速的收敛状态，则应选择较大的值。如果需要稳态误差，则应选择较小的值。但是，如果控制内部噪声值过小，则在算法收敛过程中，步长值的变化区间)很小，变步长LMS算法就会缩减为LMS算法，算法的稳态误差就会变大。选择最优噪声值和噪声鲁棒性没有理论依据，只能通过实验来确定。为了获得更快的收敛速度和跟踪速度，需要提高噪声鲁棒性和内部噪声分贝值。相反，为了得到一个小的稳态误差，这两个数据应该被减少。但是，如果两个必要参数的选取过小，变步长LMS算法就会回归到LMS算法。

利用Matlab对信号进行重采样，采用一些可以进行时频分析的工具，对采集到的声音信号进行短时傅里叶变换，积极做出正向的时频分析调动。分析信息显示，时间在不断增加的过程中，噪声频率能量分布再也做出一些细微的变化，并且变化一点一点的走向剧烈振动，峰值的范围大概在正常人能听到的20Hz～50Hz频带之内。所采集到的噪声样本也在这个低频带之间，所观察到的分量能量在这个区间内也处于较大的波动，图3为车内多通道自适应陷波主动噪声控制系统框图。

=

(

)-

(

)+

(

)

(1)

式子中，

代表收敛系数，

代表滤波参数，想要在计算中较少一些步骤和不必要的麻烦，使用离散傅里叶变换就可以将计算过程进行一定量的简化。为了可以更加主观准确的看出陷波算法的降噪性能，对收敛速度和稳态误差做出更多的对比和定义。自适应噪声陷波问题主要是由点帧外的不确定性和二级路径的不确定性引起的。从以上的控制框图中可以观察出来，二次路径中存在的问题一般都涵盖了路径中通的一些估计误差，有时候也会存在一些传感器中的误差信号，计算传递函数及其变化公式可以表示为公式3:

=

(

+1)-

(

)-2

(

)

(

)

(2)

依照最一开始的速度下降算法，可以在计算结果中得知权矢量的迭代公式，计算最终结果的公式为下列公式2：

=-

(3)

式子中，

选择越小，系统的次级通路越差；

选择越大，则反馈系统内部的稳定性越差，系统越是容易发散。当二级路径发生变化时，系统的收敛速度、最优收敛速度和最优收敛系数均发生变化。内部噪声的收敛速度和最优收敛速度都得到了提高，这就证明改变了二级路径也是可以解决问题的。可是当只是关闭一侧的前排车窗时，不管这个时候的检测结果如虎而变化，收敛系数都不会改变，也不会主动进行收敛。这就代表了单单做出收敛系数的改变是没有用的，想要产生降噪效果等于空谈，这种情况属于二次路径的完全失配现象。

2 LMS算法的汽车内部噪声主动控制

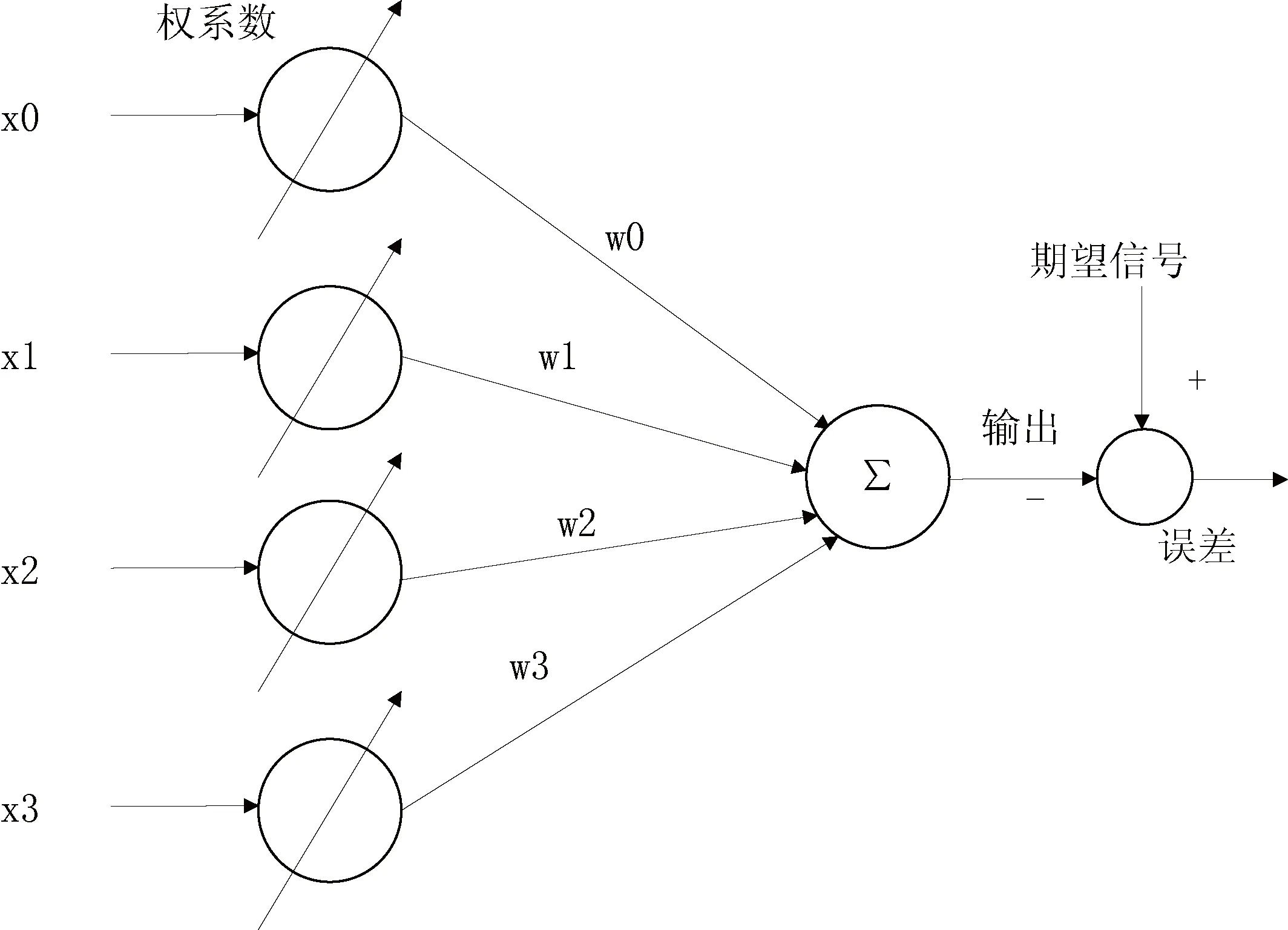
基于最快下降算法，LMS算法的实现主要包括四个步骤:第一步，权值向量初始化，选择步长因子;第二步，权值向量迭代更新;第三步要尝试判断收敛条件的相关性；第四步要观察算法是否收敛，如果不收敛，返回到之前的步骤中去，按照新的内容重新开始。在初始收敛阶段，数值较大，对应的数值也较大。当算法进入收敛状态时，值达到最小，对应的值也是最小的。所以算法可以解决固有的缺陷，当噪声值固定时，对于相同的初始误差，其对应的值较大，在收敛的初始阶段，算法收敛速度越快，对应的噪声值就越大，如果选择算法提高收敛速度，但收敛后的数值也可能较大，此时算法的稳态误差也较大。如果要求算法的收敛速度，则应选择较大的噪声值。如果需要稳态误差，则应选择较小的噪声值。值得注意的是，如果噪声陷波选择过小，则算法收敛过程中步长值的变化区间较小，当算法的稳态误差逐渐扩大时，要将变步长LMS算法更改为之前的传统算法。

由表2可以看出，在单门槛效应检验中，F统计量为20.792 8，Bootstrap计算得到的P值为0.000 0，表明在1%的显著性水平下可以拒绝不存在门槛值的原假设，即存在一个门槛值。在双门槛效应检验中，F统计量为13.361 4，P值为0.000 7，表明在1%的显著性水平下拒绝存在1个门槛值的原假设，即存在两个门槛值。在三门槛效应检验中，F统计量为3.368 6，P值为0.113 7，表明即使在10%的显著性水平下也无法拒绝存在2个门槛值的原假设，因此，我们接受存在两个门槛值的检验结果，到此结束对门槛效应的检验。

3 对比实验

3.1 实验准备

选择自适应陷波算法的N为20阶，将噪声采集其中的输入信号和期望信号前1000个采样点作为训练样本对，用自适应陷波算法建立自适应滤波器以方便在实验中使用。自适应滤波器建立后，随机选取不参与训练的采样点进行自适应滤波器去噪。经过多次实验，确定了α=1和β=1的最佳参数为α和β=1。

3.2 实验结果

依照基于智能算法的汽车内部噪声主动控制方法，确定LMS算法的步长在0.2，采样的点数之间为20个一组，以此来方便计算实验结果，基于普通算法和变步长LMS算法的自适应滤波降噪结果如图5所示。

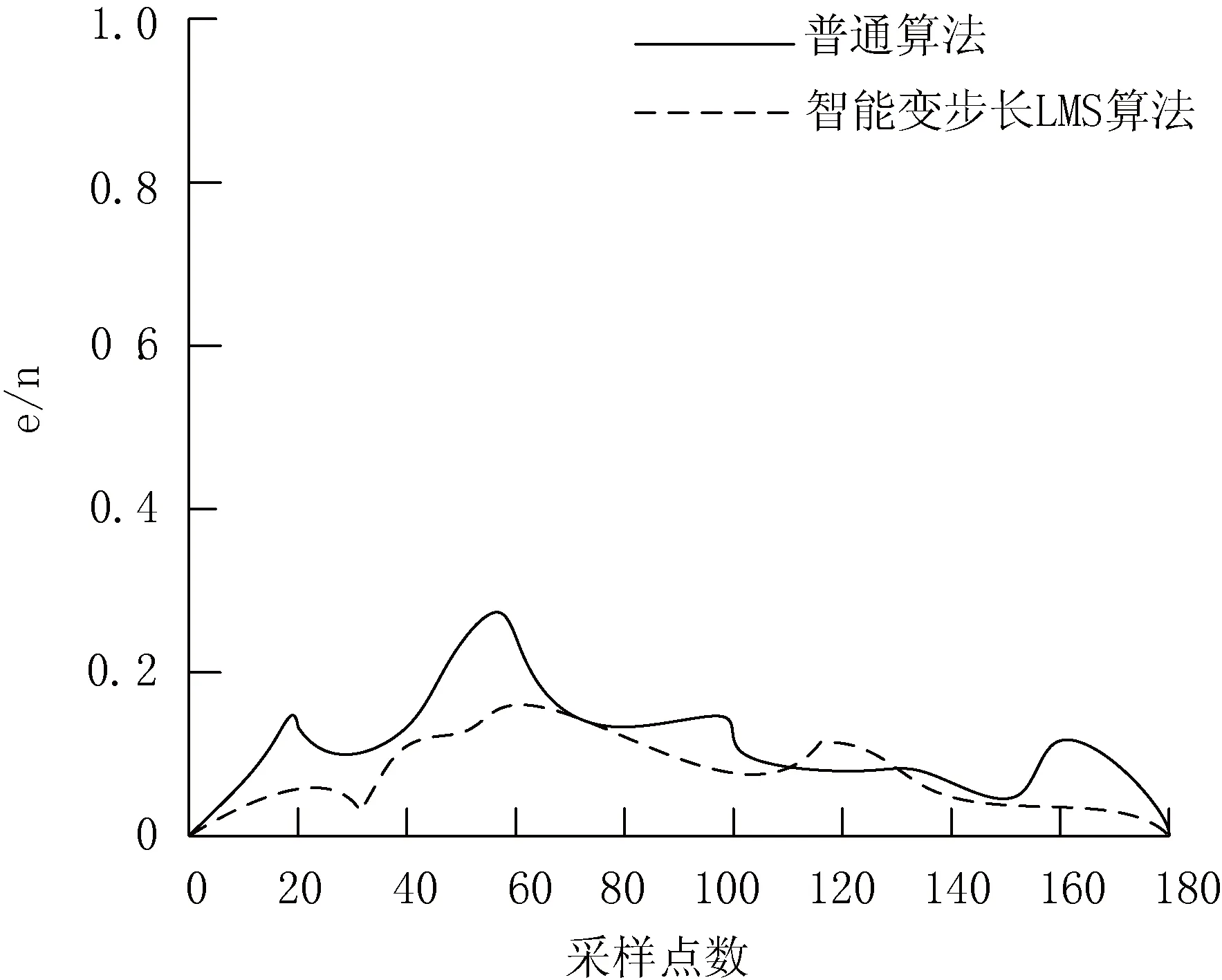
从算法收敛速度和稳态误差两个方面分析了自适应滤波降噪的结果。在相同的算法收敛条件下，传统算法最早在第100个采样点进入收敛状态，而智能变步长LMS算法在第20个采样点进入收敛状态。不仅如此，与传统算法相比智能算法的稳态误差也比较小。因此，本文提出的智能变步长LMS算法解决了传统算法的固有缺陷，该算法具有较小的稳态误差和更快的收敛速度，是一种有效的改进智能算法，基于智能算法的汽车内层噪声主动控制方法，能够有效地控制汽车内部噪声并达到最终目的。

取3.00mL硫酸根标准溶液，依照1.3.3步骤，收集滤液，考察滤液在400～500nm间吸光度值的变化，结果表明：当波长为420nm时，滤液的吸光度值最大且稳定，因此，实验选择420nm作为分析波长。

4 结束语

在分析车内噪声样本数据的基础上，对车内噪声波动进行了研究和测试。采用智能算法建立了车辆内部噪声的主动控制方法，虽然二次路径反馈方法可以控制噪声波动，但不存在二次路径完全失配的风险。与之前的传统算法的结果比较表明，变步长LMS算法克服了普通算法的固有缺陷，具有较快的收敛速度和较小的稳态误差。未来将该算法直接应用到车内噪声的实际主动控制中，会导致控制系统存在轻微的不稳定因素。在智能算法的基础上，开发考虑二次通道的自适应智能算法，可以成为实车车内制动噪声主动控制的研究重点。

[1]袁建新,刘勇.某车型车身内部噪声控制分析与应用[J].景德镇学院学报,2021,36(06):38-41.

[2]李立尧.活塞式内燃机汽车噪声控制技术研究[J].内燃机与配件,2020(24):21-22.

[3]许林倩,岳志强.混合动力汽车噪声和振动特性及其控制[J].时代汽车,2020(21):23-24.

[4]梁娜.浅析活塞式内燃机汽车噪声控制技术[J].内燃机与配件,2020(20):49-50.

[5]武守辉,潘玉龙,马东旺.汽车噪声控制技术研究[J].河南科技,2020,39(25):107-109.

[6]王明阳.浅析汽车噪声振动控制和NVH性能的开发[J].内燃机与配件,2020(05):216-217.

[7]廖华新.活塞式内燃机汽车噪声控制技术分析[J].内燃机与配件,2019(18):47-48.

[8]于洪超.汽车噪声控制方法研究[J].决策探索(中),2019(09):96.

[9]李红欢.汽车变速箱噪声源识别及噪声控制分析[J].机械管理开发,2019,34(07):146-147+209.

[10]岳中英,刘玉龙,谢凯,等.混合动力汽车噪声和振动特性及其控制[J].汽车技术,2018(11):27-31.