基于改进PSO的螺旋锥齿轮齿面测量路径优化研究

螺旋锥齿轮具有传动比平稳、承载能力强、传动噪音低以及寿命长等优点，而被广泛应用于航空、汽车、船舶等领域

。但由于螺旋锥齿轮的齿面呈超越非线性方程、形态非常地复杂，导致螺旋锥齿轮的加工和测量难度很大

。国外发达国家具有较高螺旋锥齿轮测量技术，因此研究螺旋锥齿轮的测量技术，对提高我国螺旋锥齿轮的加工和测量水平具有十分重要的意义。

高精度的测量方法直接影响着螺旋锥齿轮的加工精度。目前，三坐标测量机是测量螺旋锥齿轮齿面的有效设备，不仅可以降低测量成本，而且具有较高的测量精度

。随着三坐标测量机相关技术的发展，其测量精度越来越高、应用范围越来越广，三坐标测量技术也被广泛的应用于齿轮的精度测量。但是，如何进一步提高测量精度和测量效率一直是研究学者关心的热点问题。邢彬

建立了齿面数学模型，借助软件分析了齿面离散点和齿轮实体模型，得到了有效的实验结果。刘明亮

利用三坐标测量机和三维扫描仪对螺旋锥齿轮的齿轮测量技术进行的研究，并得到了有效的结论。武冠宏等

建立了齿面方程，通过实验对比表明了三坐标测量机的对螺旋锥齿轮的测量偏差明细小于其他测量设备。皮春琳

利用扫描式三维测头对螺旋锥齿轮进行测量研究，并完成了齿形和齿距等测量实验。张婧等

利提出了一种自适应分布法对螺旋锥齿轮齿面进行测量研究，并验证了方法的有效性。高延峰等

利用遗传算法对具有复杂曲面工件的测量路径进行了优化研究，提高了测量效率，但忽略了算法容易陷入局部最优等缺陷。

本文针对三坐标测量机在测量螺旋锥齿轮齿面时路径优化问题，建立了齿轮测量路径模型，提出了利用粒子群算法(Particle Swarm Optimization, PSO)对测量路径进行优化分析。为了提高PSO算法的效果，对权重系数和学习因子进行了改进。最后，仿真实验结果表明，本文改进的PSO算法具有较好的全局搜索能力、局部搜索能力和较高的运算效率，且能获得较好的测量路径。

1 齿面测量路径

总所周知，螺旋锥齿轮的齿面时一个非常复杂的空间曲面，利用三坐标测量机来测量螺旋锥齿轮的齿面形状，主要是预先设置好测量坐标，然后逐点进行测量。增加测量点数是提高测量精度的有效方法，但是随着测量点数的增加，测量路径的优化就显得尤为重要。当确定了测量点的坐标后，测量路径的优化直接影响着测量效率，特别是在测量点分布不均匀时，这种影响更加明显。此外，当测量路径规划错误时，势必将导致测头与工件发生碰撞。由此可见对测量路径的是必不可少的，其不仅可以减少测量过程的空运行，而且可在测头与工件不碰撞的前提下以最短的路径完成测量工作，从而提高测量效率。图1所示为本文研究的螺旋锥齿轮齿面测量路径示意图。

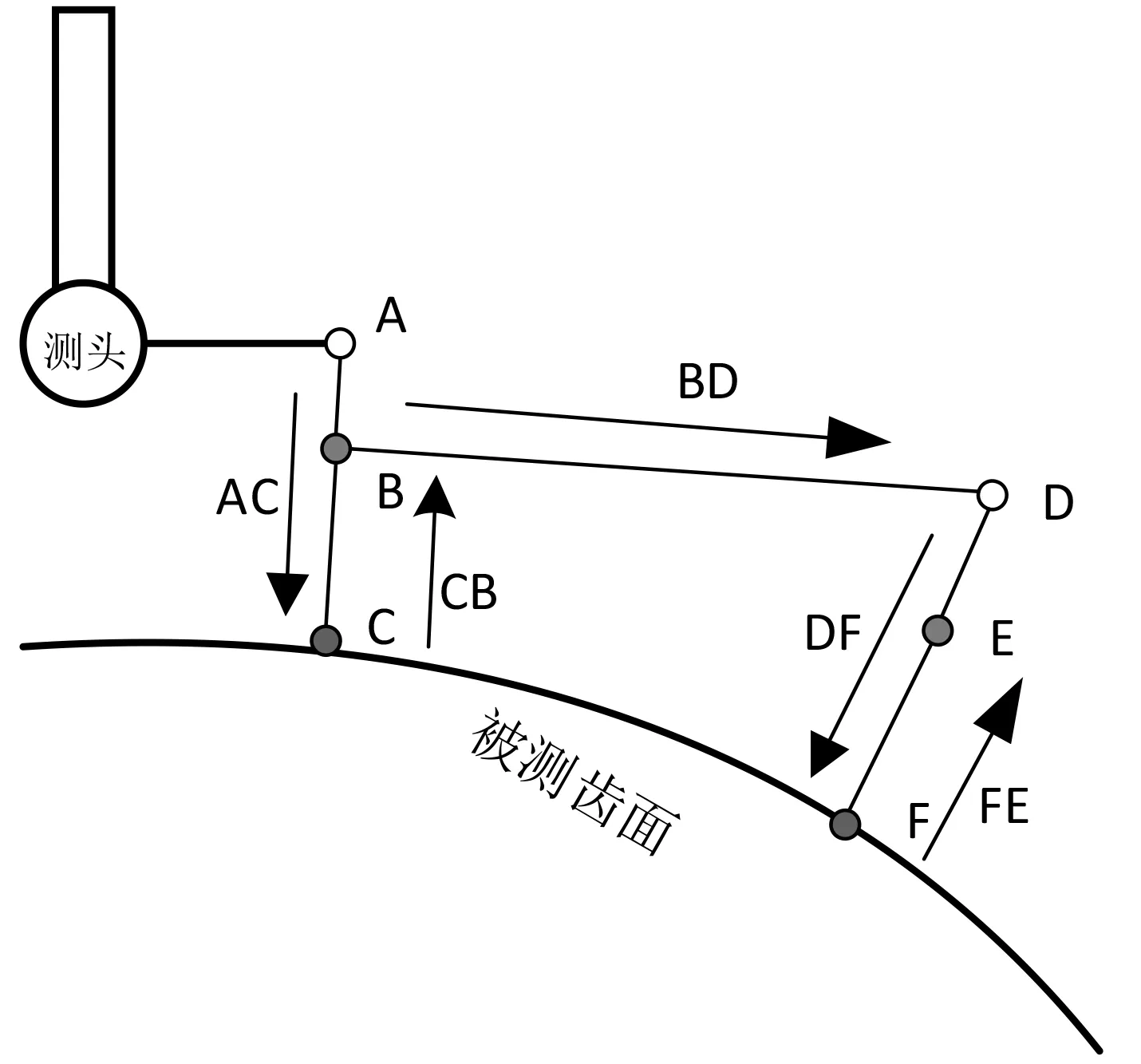
如图1所示，利用三坐标测量机在测量过程中，大致可以分为到达定位点、接近测量点和退回到回退点三个过程。首先，测头以较快的速度到达指定的第一个定位点A，然后以测量点C的法向方向运动至C点，如图AC路径所示；完成测量之后，退回至回退点B，如图CB路径所示。到此，完成一个测量点的测量工作。之后，测头运动至下一个定位点D，测量点F，回退点E完成相应的测量工作。因此，可以推出测头完成一个测量点的测量工作时，移动的距离为：

=

+

+

(1)

式中，

为定位点至目标测量点之间的距离；

为测量点至回退点之间的距离；

为回退点至下一个定位点之间的距离。

若在整个齿面测量工作中，测量点的总和为

，则齿面的测量路径可以表示为：

(2)

我们所说的理论自信不是以超自然、超人类的超验价值为目的，而是从人们的世俗生活和现实社会中揭示进步人类的现实价值目标；不是像宗教那样，用神圣的光环掩盖世俗的生活，并将之变成超验的宿命；而是致力于揭示进步人类的现实利益。它是实实在在的，而不是虚幻的、不可企及的。科学性和现实性是理论自信即科学信仰的两个最基本特征。

至于策论的内容，可以与当今公务员考试中的申论参照，因为申论就是在策论基础上发展而来的。[8]这样的考试更多的是引导士子关心国计民生，而考生也是完成了言事论政的预演，培养了相关的能力，国家也并不会期望靠着这些考生的建议来解决实际问题的。因为不是考诗赋，当然也不会完全是文学能力的比拼。

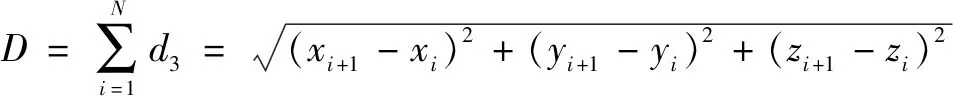
(3)

式中，(

,

,

)和(

+1

,

+1

,

+1

)分别为第

和第

+1个测量点的坐标值。

本次62例研究对象均为我院2016年12月-2017年11月接收的食管异物患者,根据不同诊治方法将其平均分为两组,对照组31例患者中,男患与女患的比例是15:16,最大年龄值时79岁,最小年龄值是2岁,均龄值数是(45.26±1.52)岁;研究组31例患者中,男患与女患的比值是14:17,最大年龄值是78岁,最小年龄值是3岁,均龄值数是(44.89±2.03)岁,对比两组患者基础资料可知,未见显著差异,统计学无意义(P<0.05)。

2 PSO算法的改进

2.1 PSO算法

粒子群优化算法是由Eberhart博士和Kennedy博士发明的一种进化算法

，其源于对鸟群捕食行为的研究。在PSO算法中，将所要优化问题的解都认为是搜索空间的一只小鸟，并抽象为一个微小的粒子，延伸至N维空间。在N维空间中的每一个粒子描述为一个相对应的矢量，粒子在空间中的飞行速度也描述为一个相对应的矢量。PSO算法本质上是一种迭代优化的算法，利用迭代来寻找最优值。

权重系数直接影响了粒子对当前速度的继承量、粒子探索能力和开发能力的均衡性。为了克服传统权重系数线性递减无法找到最优点而陷入局部最优的缺点，本文采用随机权重法。首先，若在算法初期粒子接近最好的点，随机权重法将产生较小的权重值 ，提高算法的收敛速度；若算法在初期无法找到最好的点，随机权重法可使得算法跳出局部最优。具体公式如下：

过了立秋以后，全国的气温已不再火热，复合肥市场也平稳度过“避暑”阶段，之所以说复合肥市场过去是在避暑，是因为今年的夏季肥销量不佳，并没有达到预期效果。目前已进入秋季，秋季是一年中最后的一个用肥旺季，所以秋肥市场也是各大企业的“兵家”必争之地。目前主流厂商出厂报价：45%氯基复合肥报价在2100-2200元/吨，45%硫基复合肥报价在2250-2350元/吨。

传统的PSO算法虽然具有较好的优化性能，但是其在迭代过程中容易陷入早熟和局部最优。因此为了提高PSO算法的性能，本文提出了以下方法对其进行改进：

,

(

+1)=

,

(

)+

[

,

-

,

(

)]+

[

,

-

,

(

)]

,

(

+1)=

,

(

)+

,

(

+1),

=1,2,…,

(4)

式中：

为惯性权重；

,

为正的学习因子；

,

为随机数，且

,

∈

(1)。

选择的PBL教案：①甲状腺疾病、腹壁疝；②胃肠疾病；③肝胆疾病；④胰腺疾病；⑤门脉高压；⑥腹部损伤；⑦急性腹膜炎；⑧急腹症；⑨周围血管疾病。

通过上述分析可以发现，不论测量点的选取情况如何，

和

均为固定值，即齿面的测量路径只受

的影响。因此齿面测量路径的优化目标函数可以进一步表示为：

2.2 PSO算法的改进

政策一：6月5日，生态环境部、中央文明办、教育部、共青团中央、全国妇联等五部门联合发布《公民生态环境行为规范（试行）》，倡导简约适度、绿色低碳的生活方式，引领公民践行生态环境责任，携手共建天蓝、地绿、水清的美丽中国。

(1)权重系数的改进

（1）从建筑力学入门教学的内容来看，一般都是要先介绍概念，例如力学、建筑力学，然后讲解建筑力学的研究对象和研究任务，不同的教材虽各有差异，但万变不离其宗。然而教师如果按照这样的内容一点点讲给学生，学生要么听过就忘，要么注意力不集中。教师讲的费劲，学生听得没劲，很难达到预期的效果。

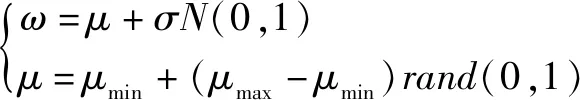
(5)

据统计，2018年云南大学的在校留学生共923人，在“一带一路”五周年之际，留学生数量相比2013年增加了70%[37]。本研究选取云南大学校本部的留学生为研究对象。据实地调查，云南大学校本部的留学生生源主要来自于东南亚、南亚、东亚及欧美各国，以东南亚、南亚国家为主。留学生多为本科生、语言班学生，近年来，研究生、博士生的比例有所提高。

通过式(5)可以发现，将权重系数设定为服从正态随机分布的随机数，这样使得

算法在初期如果粒子接近最好的点，将具有较小的权重值，提高算法的收敛速度；如果在初期

算法未能找到最好的点，则可使算法轻松的跳出局部最优。

(2)学习因子的改进

式中，

(0,1)为服从标准正态分布的随机数；

(0,1)为0至1之间的随机数。

在

算法中，除了权重系数之外，学习因子对PSO算法的性能同样也具有重要的影响。对于PSO算法，在算法初期较大的

和较小的

，能使其具有更好的全局搜索能力，可较大范围的寻找最优解；在算法后期较大的

和较小的

，能使其具有更好的局部搜索能力。因此，为了提高综合PSO算法的全局搜索能力和局部搜索能力，本文采用非线性变化方法对学习因子进行改进，具体如式(6)所示：

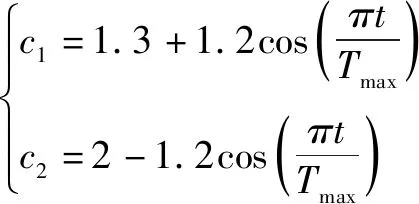
(6)

式中，

为最大迭代数，

为当前迭代数。

在PSO算法运算时，首先初始化一群随机粒子，然后所有的粒子会跟随当前最优粒子在N维空间中搜索，直至找到最优解。若在N维空间中第i个粒子的速度为

=(

,1

,

,2

,…,

,

)，位置为

=(

,1

,

,2

,…,

,

)，则在迭代过程中，粒子会跟踪个体极值

=(

,1

,

,2

,…,

,

)和全局最优解

来更新自己。即，粒子将以式(4)更新自己的速度和位置：

通过式(6)可以发现，随着迭代数

的增加，使得在算法初期具有较大的

和较小的

，在算法后期具有较大的

和较小的

。因此，综合了PSO算法的全局搜索能力和局部搜索能力，提高了算法的运行效率。

2009年，微量物质示踪技术在绥中油田[14]进行了应用，现场试验表明微量物质示踪剂具有用量少、检测精度高、对环境无污染等优点。随后大港油田[15]也取得了良好的现场使用效果。

2.3 改进PSO算法的流程

Step1：设置PSO算法的相关参数(种群大小、最大迭代数，随机权重平局值的最大值和最小值，随机权重方差)，随机初始化种群中各粒子的位置和速度；

Step2：计算各个粒子的适应度值，保存各个粒子的当前位置和适应值，并比较所有的粒子的适应值，将最优的赋值于

；

Step3：利用式(4)更新粒子的速度和位置；

Step4：利用式(5)和式(6)更新权重和学习因子；

Step5：将各个粒子的适应值和最好的位置进行比较，如果粒子的适应值较好，则将其视为当前的最好位置，并且将当前的

和

进行更新；

Step6：判断是否满足算法停止条件。若满足，算法停止，输出最终结果；否则算法跳转至Step2。

3 齿面测量路径优化

利用三坐标测量机测得螺旋锥齿轮齿面测量点的分布情况，如图2所示，一共有70个点。为了验证本文提出算法的性能，分别利用遗传算法、传统PSO算法和本文改进的PSO算法对测量路径进行优化分析，对比三种算法的优化结果。由于算法的优化过程具有一定的随机性，为了使比较结果更有说服力，对三种算法分别独立运行30次，并取其均值进行比较，三种算法的运行结果如表1所示。

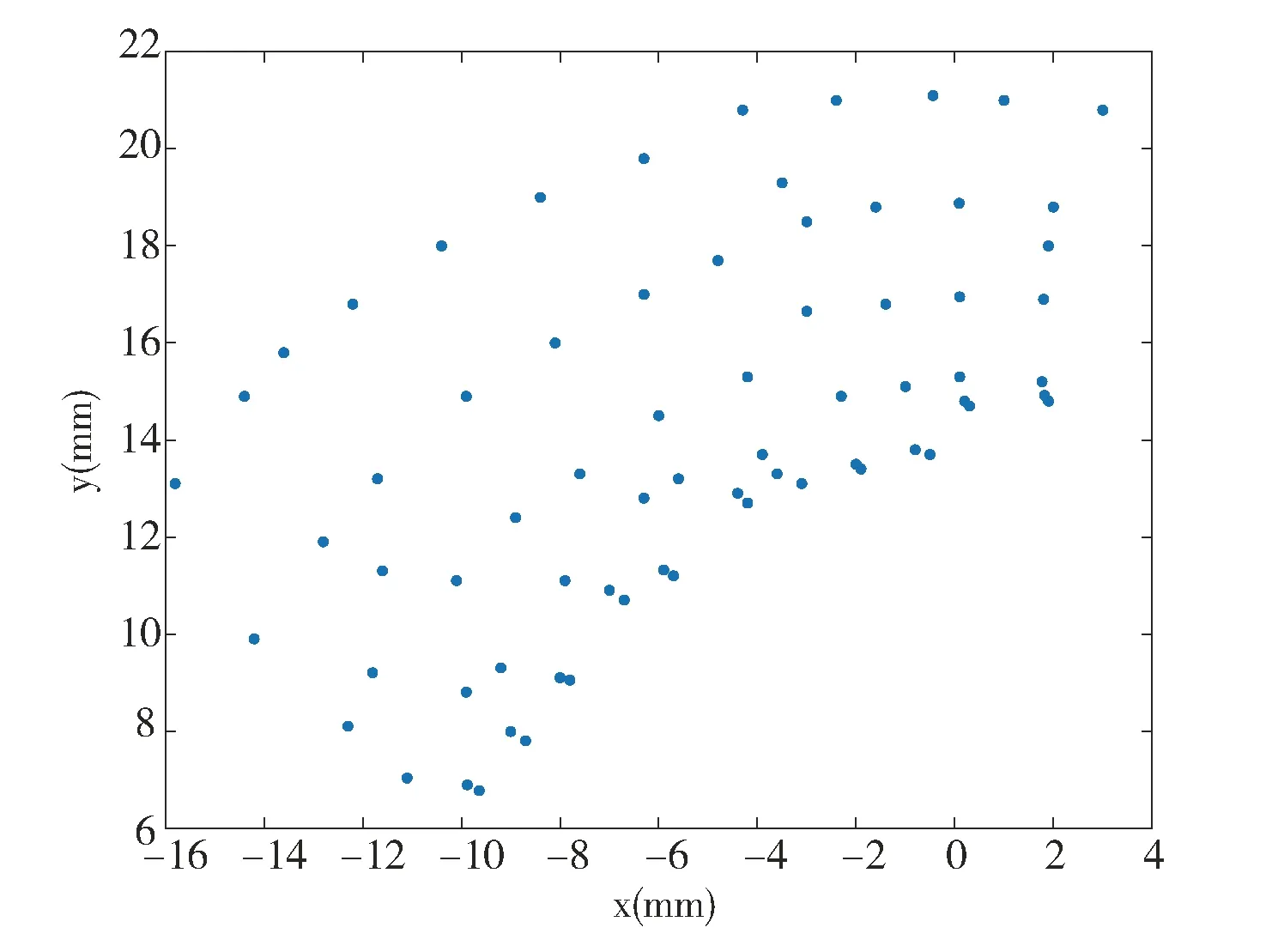
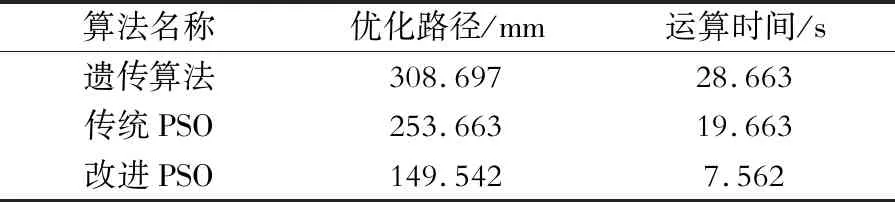
分析表1对比结果可知，本文提出的改进PSO算法求得的最优路径优于其他两种算法，传统PSO次之，遗传算法的效果最差。此外，对比算法的运算时间可以发现，本文提出的改进PSO算法同样具有最高的运算效率。结果表明，本文提出的改进PSO算法由于其他两种算法。

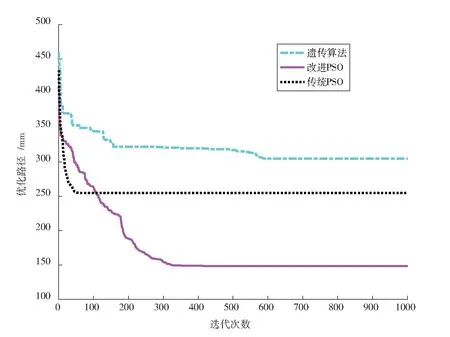
为了能更加直观的观察算法的运行过程，图3给出了三种算法某次运行时的情况对比。从图中可以看出传统PSO算法很快就陷入了局部最优、遗传算法虽然在开始阶段可以跳出局部最优，但是其收敛能力比其他两种算法差，本文提出的改进PSO算法虽然收敛速度较慢，但具有较小的适应度值。进一步表明，本文提出的随机权重法和非线性变化学习因子，使算法具有较好的全局搜索能力和局部搜索能力，能跳出局部最优化，寻找到真正的最优解，提高了算法的运行效率。

4 结论

提出的改进PSO算法获得的测量路径明显短于其他算法，且运行时间较短。因此，本文提出的方法可以有效降低螺旋锥齿轮齿面测量成本、提高测量效率，为螺旋锥齿轮齿面测量路径优化提供有效的参考借鉴。

[1]叶君,朱光照,仉凤权,等.航空螺旋锥齿轮数字化闭环制造技术探析[J].中国设备工程,2021(17):220-222.

[2]张振华,王欢锐,周彬.某客车驱动桥螺旋锥齿轮早期打齿原因分析[J].汽车工艺与材料,2020(03):54-57.

[3]姜义尧,胡小舟,孙凯.某型直升机中减速器飞溅润滑流场特性分析[J].航空动力学报,2018,33(12):3032-3040.

[4]王永旭,阿达依·谢尔亚孜旦,刘明亮.双正交小波对球面渐开线螺旋锥齿轮齿面拟合的研究[J].机床与液压,2022,50(02):1-7.

[5]宋碧芸,唐进元,容铠彬,丁撼.减小螺旋锥齿轮齿面加工误差的参数修正方法[J].西安交通大学学报,2022,56(02):101-109.

[6]唐进元,邢彬.基于三坐标测量机的螺旋锥齿轮加工参数反调修正[J].北京工业大学学报,2010,36(11):1451-1456.

[7]刘广东,刘心宇,曹阳.三坐标测量机实测元素与数字模型最佳拟合的应用[J].机械工程师,2022(02):11-13.

[8]唐少博,朱江,龙宽,等.三坐标测量机及配合使用的光学转台测量结果不确定度的评估[J].内燃机与配件,2022(02):125-127.

[9]邢彬. 螺旋锥齿轮齿面三坐标测量机测量关键技术与测量数据应用研究[D].中南大学,2010.

[10]刘明亮. 螺旋锥齿轮测量关键问题基础研究[D].新疆大学,2021.

[11]武冠宏,赵韩,吴占雨,等.基于三坐标测量的螺旋锥齿轮检测关键技术[J].合肥工业大学学报(自然科学版),2015,38(04):437-440.

[12]皮春琳. 基于扫描式三维测头的螺旋锥齿轮测量方法研究[D].重庆理工大学,2019.

[13]张婧,胡海波,郑惠江,等.螺旋锥齿轮齿面测量点分布新方法研究[J].机械科学与技术,2019,38(11):1745-1751.

[14]高延峰,王孙安.基于遗传算法的自由曲面测量路径规划[J].机床与液压,2003(06):275-276+332.

[15]Kennedy J, Eberhart R C. Particle swarm optimization[C].Proceedings of International Conference on Neural Networks. New York: IEEE, 1995: 1942-1948.