基于等几何分析的参数化曲梁结构非线性动力学降阶模型研究

2022-08-01郭玉杰吴晗浪李迎港吴剑晨

工程力学 2022年8期

郭玉杰，吴晗浪，李薇，李迎港，吴剑晨

(南京航空航天大学飞行器先进设计技术国防重点学科实验室，南京 210016)

现代工业及军事装备结构往往较为复杂，因而对设计与分析工具提出较高要求。采用传统数值手段(如有限元法等)进行结构分析时，常需要细密的网格以获得较高精度解，往往会导致维数灾难问题(curse of dimensionality)，特别对于需要反复迭代求解的复杂问题，比如非线性动力学、结构多学科优化、多场耦合等仍过于耗时[1]。

模型降阶(model order reduction)方法通过构造全阶模型(full order model)的低阶近似模型有效降低了求解问题的维度，同时也保留了原阶模型的主要信息从而保证了较高的计算精度。常见的模型降阶方法包括模态叠加法[2]、模态导数法[3-4]以及正交分解法[5-6](proper orthogonal decomposition, POD)等，但对于非线性动力学问题，上述常规方法还存在一定问题，比如模态叠加法需要不断更新模态空间，POD 方法需要不断更新全阶模型的内力、刚度矩阵等，这显著增加了计算复杂度并降低了计算效率[7]。针对这一问题，Astrid等[8]提出了一种MPE (missing point estimation，缺失点估计)方法，其通过计算在预先选定的空间点处的函数值，再利用gappy POD 方法将其投影到降维空间以实现计算效率的提升。Rewienski 等[9]提出了TPWLMOR (trajectory piecewise linear model order reduction，轨迹分片线性模型降阶)方法，其在一系列采样点上采用Krylov 投射对非线性函数进行降阶，再对降阶模型加权求和从而可以实现非线性函数的逼近，但对于一些复杂非线性函数，采用低阶分片多项式逼近效果不佳。Gaonkar等[10-11]在此基础上提出了一种改进的TPWLMOR方法，有效提升了降阶模型在非线性动力学计算方面的精度与效率。满兴博等[12]提出了一种非线性Galerkin 方法，有效提升了降阶模型精度。Barrault[13]及Grepl 等[14]提出了一种经验插值法(empirical interpolation method, EIM)，其采用一组经验基函数的线性组合来近似非线性项，组合系数可通过插值求解得到，在此基础上可通过greedy算法选取合适的snapshots 作为降阶基函数构造降阶模型[15]，但EIM 不能扩展到任意非线性函数。Chaturanabut 等[7]基于EIM 提出了一种离散形式的经验插值方法(DEIM)，其采用POD 基底作为输入并适用于任意类型的常微分方程，相比于EIM，其离散的变体应用范围更广，且无需施加额外的基底变换，同时两者的计算结果在数学上是等价的，因此受到了广泛关注。

在参数化降阶模型研究方面，传统方法存在与非线性降阶模型类似的困难，即难以实现模型的输入参数与微分算子的解耦，从而对于每个未知输入参数都需要重新计算系统的刚度矩阵等，计算效率不高[16]。针对这一问题，许多学者尝试将有限元模型与降阶模型进行解耦，以实现线下/线上的计算模式(offline/online procedure)[17-19]。在线下模式中，其计算复杂度及计算量与所求问题的有限元模型相关，但可以预先计算并存储结果，在线上模式中，其计算量以及计算复杂度只与降阶模型有关，结合后验误差估计方法，即可以实现实时、高精度的降阶模型求解。当所求解的模型与输入参数具有仿射关系时，可以将输入参数与微分算子分离，再结合降阶模型方法即可实现线下/线上的计算模式。但通常情况下这种仿射关系并不存在或者难以建立。许多学者[7,13-14,20-21]通过POD 或者EIM/DEIM 方法实现了参数化模型的降阶，从而可以进行快速设计与优化。此外，在模型的参数化描述方面(特别是几何形状)，还缺乏统一、高效的手段，并且对于不同的几何形状输入参数，需要重复建立有限元模型，当几何模型较为复杂时，其耗费的网格划分等前处理时间则较为显著[22-23]，造成这一问题的根本原因在于CAD 与CAE 中几何模型的描述方式存在不一致[23]。在CAD 中，几何模型一般是以非均匀有理B 样条(NURBS)或者构造实体几何(CSG)的方式来描述，而在CAE 中(比如有限元)，其模型一般是以线性或二次插值的方式来构造，是真实几何的一种近似。

等几何分析[23]的基本思想是将CAD 中描述几何形状的NURBS 引入到等参有限元中，通过统一的几何描述可以消除产品设计过程中CAD 与CAE 之间反复的数据转换过程，从而节省了大量的前处理时间。等几何分析自2005 年提出以来迅速成为计算力学以及计算几何领域的研究热点[24-27]，相比于传统有限元方法，等几何分析其具有几何精确、光顺以及高阶连续等优点，因此特别适合于薄壁类结构的分析、优化等[28-38]。在等几何降阶模型研究方面，一些学者考虑了等几何分析在模型几何形状描述、高效的CAD/CAE 模型转换等方面的优势，将其嵌入到了降阶模型中。宋敏[39]研究了带参数椭圆形方程的等几何分析及POD 模型降阶问题，验证了模型降阶的有效性。Manzoni 等[40]结合了等几何边界元以及降阶模型实现了实时的计算流体动力学分析，其对NACA 翼型采用了参数化描述并利用EIM 方法近似实现了参数的仿射关系。Salmoiraghi 等[22]结合了自由形状变换(free form deformation，FFD)以及等几何分析进行参数化建模，实现了以较少参数描述复杂形状，并且保证了设计模型与分析模型的无缝融合。Ding 等[41]采用等几何分析、POD 以及DEIM 研究了结构动力学问题，其结合了两种时间积分方法，有效抑制了高频振荡。Rinaldi[20]采用了EIM/DEIM 以及等几何分析研究了薄壳结构的参数化模型降阶问题，结果显示只需要少数DEIM 插值单元以及降阶基函数即可实现高精度、快速的参数化线性静力学分析。此外，一些学者还将等几何降阶模型应用到了结构优化[42]、裂纹扩展[43]、结构屈曲[44]等方面。

综上所述，将等几何分析的思想与降阶模型相结合具有广阔的应用前景，因此许多学者在这方面做了初步探索，但针对参数化的薄壁结构的非线性动力学降阶模型方面的研究还未有涉及。本文拟选取平面曲梁结构作为研究对象，采用等几何分析、POD-DEIM 方法研究其参数化的非线性动力学模型降阶问题。

1 NURBS 及几何描述

非均匀有理B 样条(NURBS)是计算机辅助设计领域用来表示曲线曲面的标准函数之一，其能够精确描述圆形等圆锥曲线，其定义为：

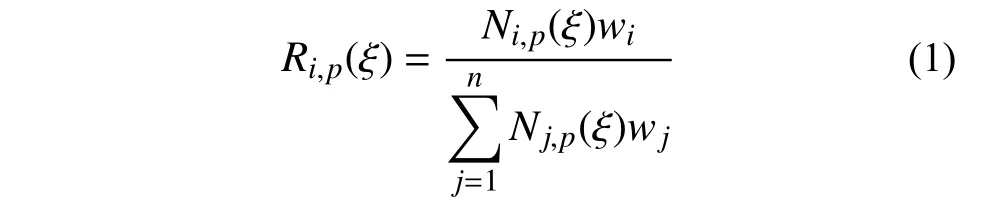
式中：p为NURBS 基函数的阶数；n为基函数的个数；Ni,p(ξ) 为p阶B 样条函数；wi为对应的权重。阶数为p的B 样条函数Ni,p(ξ)可由一给定的单调不减的节点序列 Ξ={ξ1,ξ2,···,ξn+p+1}并结合Cox-de-Boor 迭代公式求得：

由式(2)和式(3)可知，B 样条函数Ni,p(ξ)只在区间 ξ ∈[ξi,ξi+p+1)上非零，即每个B 样条函数均跨越p+1 个节点区间。同时，每个节点区间上均包含p+1 个非零的B 样条函数。除此之外，所有B 样条函数均为非负，满足单位分解性质。B 样条函数在节点处(即单元交界处)具有Cp-k次连续的特性，其中k为节点的重复度，因此可以通过插入与删除节点操作来调节单元间的连续性。当节点矢量两端的节点重复度均为p+1 次时，其被称为开放型节点向量(open knot vector)。

一条p次NURBS 曲线的定义为：

图1 NURBS 曲线及NURBS 基函数Fig. 1 NURBS curve and NURBS basis functions

二维NURBS 曲面以及三维实体可通过张量积的形式构造，具体可参见文献[45]。

2 等几何平面曲梁非线性动力学模型

2.1 平面曲梁运动学及本构关系

本文所讨论的曲梁模型基于Euler-Bernoulli 假设，即忽略剪切变形和横截面转动的影响。本文中所有与初始构型(reference configuration)相关的参数均用大写字母表示，与变形状态(deformed configuration)相关的参数均采用小写字母表示。

图2 给出了平面曲梁模型示意图，其可由一中性轴和一系列横截面所表示。图中X以及x为曲梁中性轴的位置向量，且x=X+u，u为曲梁的位移向量。为了便于计算，需要在中性轴上定义一个活动标架 {a1,a2,a3} ，其中向量a1表示沿中性轴的单位切向量，向量a2及a3是位于曲梁的横截面上并且互相正交的单位向量。单位向量a1可由下式计算得到：

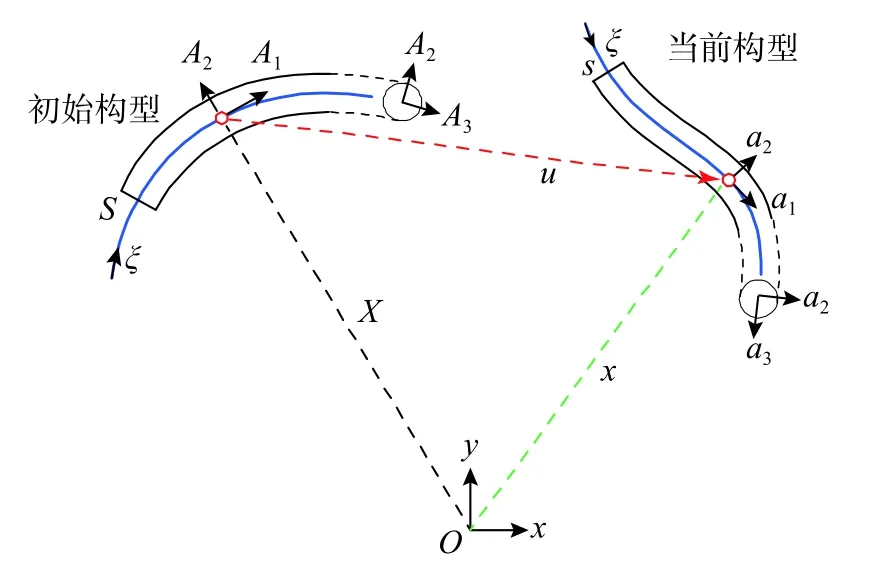
图2 初始构型与当前构型Fig. 2 Reference and current configurations

式中，ds为中性轴的弧长微分。不失一般性，选取a3为垂直于xy平面的单位向量，则a2可表示为a1×a3。

对于二维平面曲梁，其应变关系可由薄膜应变ε 以及弯曲应变ρ 表示，其表达式分别为：

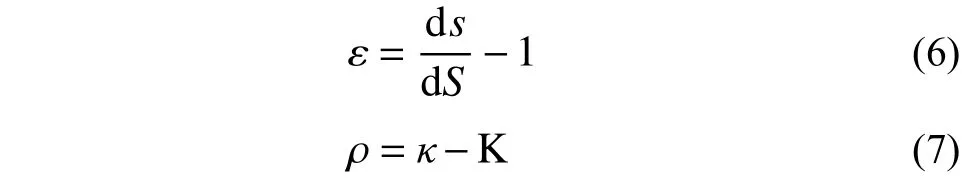
其中，弧长微分以及曲率可分别表示为：

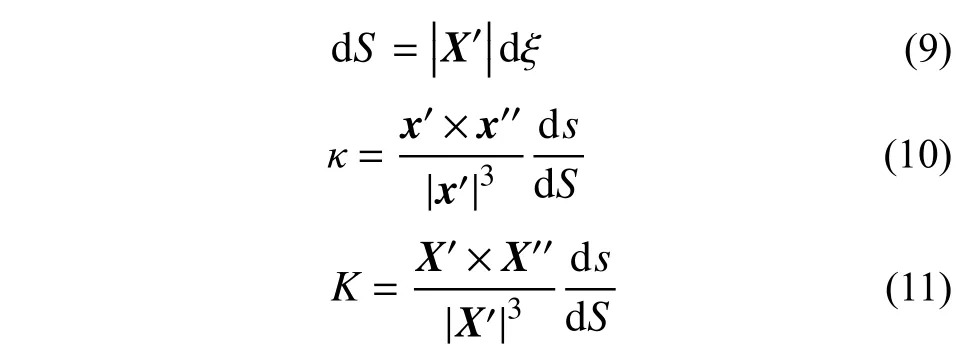
其中，上标 (·)′以及 (·)′′表示对参数坐标的一次和二次导数。根据式(4)可得：

对于弹性问题，基于圣维南原理，薄膜力与薄膜应变、弯矩与弯曲应变有如下关系：

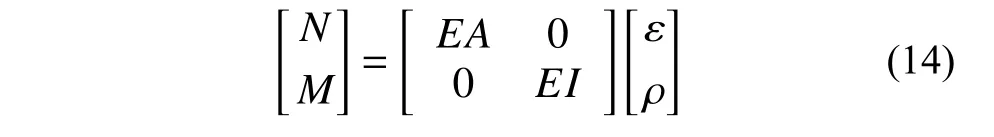
式中：E为弹性模量；A为横截面积；I为截面惯性矩。

2.2 控制方程及等几何离散

对于几何非线性问题，平面曲梁的动力学控制方程可表示为：

式中：S为曲梁中性轴的长度； δ为泛函变分；ρ0为曲梁的密度；N=N A1，M=MA3为向量化的薄膜力以及弯矩。此外，q0为分布力，p0为集中力。

基于等几何分析的思想，采用描述中性轴的NURBS 基函数插值位移场函数及其变分：

式中：Ui为第i个控制点的位移未知量；R和U分别为NURBS 基函数和位移未知量的向量集合。

将式(17)代入式(15)，并利用 δUi的任意性，得到半离散的平衡方程：

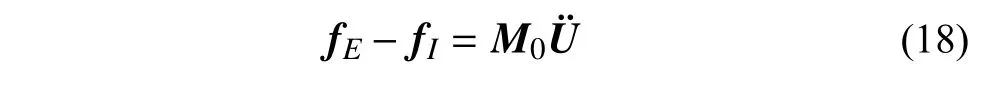
式中，M0为平面曲梁的质量矩阵，可表示为：

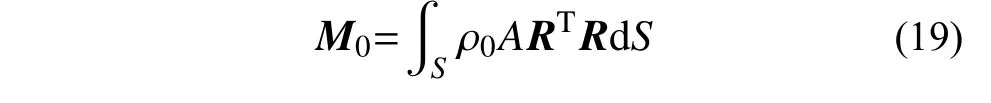
式(18)中，fI和fE分别表示曲梁的内力和外力向量，其表达式为：

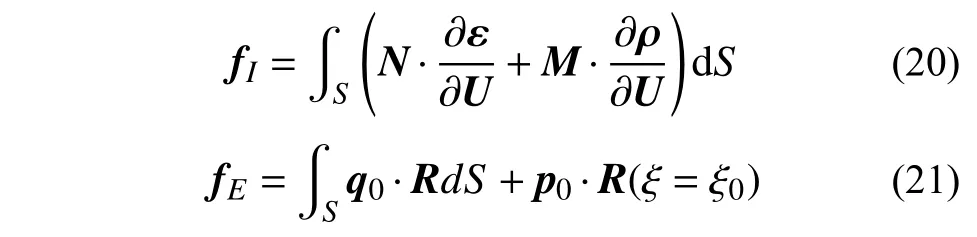
式中， ξ0为集中载荷施加位置所对应的参数值。

2.3 非线性动力学求解

平面曲梁的半离散平衡方程式(18)为时变、非线性方程，一般可通过时间积分并结合牛顿迭代进行求解。为便于说明，式(18)可改写为：

式中：t为当前时间步；Δt为时间增量。

为了寻求t+Δt时刻的平衡状态，可采用HHT-α时间积分方法，其需要定义一个动态残余力向量：

式中，α 为时间积分常数，可以调节系统的数值耗散能力，通常取 α=-0.05[46]。此外，内力的下标0 表示当前时刻的初始状态。与Newmark 方法类似，HHT-α 方法假设加速度在时间步内线性变化，因此，可以推导得出以下关系：

根据式(25)可求得t+Δt时刻的加速度：

式中， ΔU=Ut+Δt-Ut为位移增量。

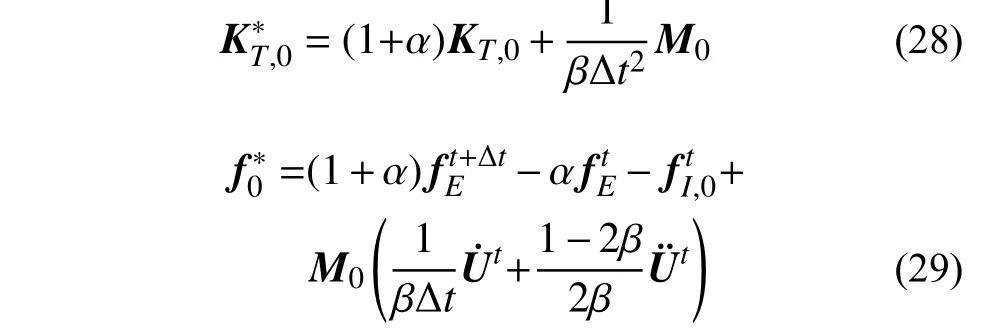
式中，KT为平面曲梁的刚度矩阵，可由内力向量fI的线性化得到，具体表达式为：

当把平面曲梁位移场U设置为当前载荷步的初始位移时，即可得到KT,0以及fI,0的表达式。

基于式(27)可得到初始载荷增量 ΔU1，从而可以更新内力向量、加速度及刚度矩阵等变量，并进行迭代求解。图3 所示为采用HHT-α 时间积分方法进行几何非线性动力学分析的算法流程。

图3 HHT-α 时间积分算法流程图Fig. 3 HHT-α time integration scheme for nonlinear dynamic analysis

3 POD-DEIM/MDEIM 模型降阶方法

3.1 模型降阶简介

假设不考虑平面曲梁的阻尼，在某一时刻系统平衡方程的离散形式可以表示为：

其中，KT,M0∈Rn×n,U,fE∈Rn×1。

其中，rROM为代入近似公式(32)产生的残差向量，其位于正交基底所张空间之外且正交于，因此如下关系式成立：

由于降阶后系统维度远小于原阶模型的系统维度(k≪n)，因此，可以提升系统求解速度，但降阶基底的选择对于降阶模型的求解精度至关重要。

3.2 POD：降阶模型基底生成

特征正交分解(POD)通过搜集不同时刻、不同参数下结构的响应快照(snapshots)，再通过奇异值分解(singular value decomposition, SVD)可获得一系列相互正交的基底向量以及对应的奇异值。

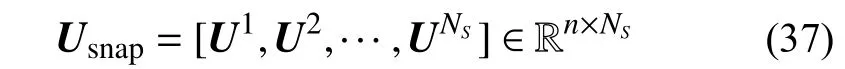
假设结构响应快照集合为：式中，NS为所搜集的快照向量个数。对Usnap采用SVD 分解，得到：

式中：V∈Rn×n为left-hand 矩阵，包含n个互相正交的单位向量 [v1,v2,···,vn]；W∈RNS×NS为right-hand矩阵，包含NS个正交向量；Σ=diag(σ1,σ2,···σn)∈Rn×NS，其包含n个奇异值σi=(i=1,2,···,n)，且σ1≥σ2≥···≥σn＞0 每个奇异值 σi的大小代表对应的基底正交向量vi占整个系统能量的比重。

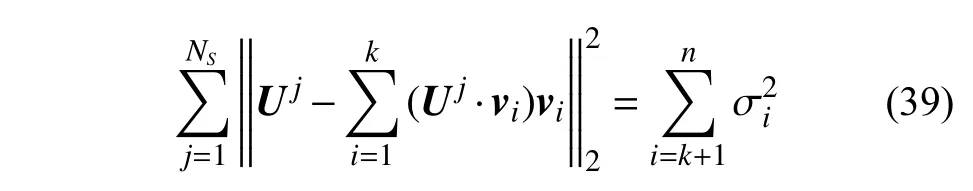
假设选取前k(k≪n)个正交向量作为模型降阶基底，则其对于快照集在最小二乘意义下的逼近误差可表示为：即可以通过剩余的n-k个奇异值的平方和来估计模型降阶基底的逼近误差。随着所选取的基函数个数k的增大，其逼近误差迅速减小，表明基函数所捕获的能量占快照集总能量的比例迅速提升，其所捕获的原系统的信息就越丰富。

3.3 DEIM/MDEIM 差值算法

对于非线性、参数化问题，在迭代求解过程中，往往需要更新结构的刚度矩阵以及内力向量，以准确捕捉结构的响应，这显著影响了降阶模型的求解效率。

离散经验插值方法(DEIM)提供了一种有效降低非线性函数计算规模的方案，采用DEIM 方法，只需计算少数给定位置的元素，再通过DEIM插值矩阵即可实现非线性项的近似表示，大大降低了非线性项的计算时间。其基本原理如下。

假设曲梁的内力向量fI所在的n维空间可由一组正交单位向量Z=[ζ1,ζ2,···,ζn]∈Rn×n所描述，且 ζi(i=1,2,···,n)按照重要性从大到小排序。与模态叠加法类似，内力向量fI可由Z的前m(m≪n)阶基向量近似得到：

式中：Zm=[ζ1,ζ2,···,ζm]∈Rn×m为前m阶基向量；c=[c1,c2,···,cm]∈Rm×1为系数向量。

式(40)为过约束方程组，因此需要选择基底Z中的m行进行求解，其可以通过布尔矩阵P实现：

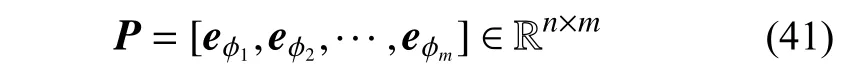
其中，eφi∈Rn×1为单位向量，且在位置φi(1≤φi≤n)处为1，其余位置均为0，式(40)左乘PT可得：

继而可以得到：

将式(43)代入式(40)可得：

其中，矩阵D为DEIM 插值矩阵。

由式(44)可知，内力向量fI可以由布尔矩阵P、基函数Zm以及特定位置φ=[φ1,φ2,···,φm]∈Rm×1处的内力向量本身近似得到，因此，在进行有限元计算时，只需要计算特定位置φ=[φ1,φ2,···,φm]处的内力值，再通过插值矩阵D即可重构得到完整的内力向量，大大节省了计算时间。

在DEIM算法中，基底向量Zm以及位置坐标φ=[φ1,φ2,···,φm]的选取对于算法的精度及稳定性至关重要，通常Zm可以选为由式(38)得到的POD 基底向量V，而位置坐标φ=[φ1,φ2,···,φm]则可以通过算法1 实现。

算法1 中函数 max{·}用于选取向量的最大元素并返回其位置坐标，其通过选取最大误差元素的位置并在下一次迭代中精确插值该位置元素，从而能够实现误差的可控，因此，残差向量rD在所选取的位置φ=[φ1,φ2,···,φm]处为0。

算法1. DEIM 算法

算法1 可以用于非线性向量的插值近似，而对于刚度矩阵，其排列方式为矩阵形式，因此可以将其按照列向量的形式进行排列，再利用DEIM方法进行插值，最后再重新按照矩阵形式进行排列即可得到插值近似的刚度矩阵，该方法可以称为 MDEIM(matrix discrete empirical interpolation method)。

值得注意的是，对于求解带有阻尼的结构动力学问题，当其阻尼矩阵为时变或者非线性变化时，也可通过上述POD-DEIM/MDEIM 方法进行模型降阶，首先搜集阻尼矩阵的快照集，进行奇异值分解得到一组基底向量Zm，再采用DEIM/MDEIM方法生成插值位置坐标向量 φ，即可构造阻尼矩阵的插值矩阵D，进而实现阻尼矩阵的快速计算。

当获得插值位置向量 φ之后，需要计算这些位置处的元素值，而每个位置元素均有与之相对应的控制点，根据NURBS 几何以及NURBS 基函数的性质，每个控点均对应一个跨(p+1)个单元的基函数，因此需要在不同单元上计算该基函数对于非线性项的贡献，基于这一规律，即可以快速地计算出位置 φ处的值，从而得到整个非线性项的近似表达。

4 数值算例

4.1 两端固支半圆弧曲梁

如图4 所示为两端固支半圆弧曲梁模型，其横截面宽度与高度分别为b=h= 25.4 mm，曲梁半径R= 1705 mm，弹性模量E= 68 975 MPa，密度为 ρ0=2.6086×10-9t/mm3。

图4 两端固支半圆弧曲梁模型Fig. 4 Half-circle arc with clamped boundary conditions at both ends

首先，研究等几何曲梁单元的收敛特性。该曲梁中部受集中力载荷F= 100 N，分别采用2、3、4 次NURBS 单元进行离散，并进行几何非线性静力分析，其中点位移的收敛曲线如图5 所示。作为对比，图5 中列出了ABAQUS 参考值，其采用了包含剪切自由度的B21 铁木辛柯梁单元，并且采用了缩减积分来控制剪切和薄膜闭锁。对比结果显示，当采用3 阶和4 阶NURBS 单元时，等几何模型收敛速度快于ABAQUS 梁单元；当阶数较低为2 阶时，收敛速度较慢。主要原因为：本文采用的等几何曲梁单元为无剪切自由度的欧拉-伯努利梁单元，当阶数较低时，存在薄膜闭锁问题，当提升单元阶数时，薄膜闭锁得到显著缓解，因而提升了收敛速度。

图5 两端固支半圆弧曲梁位移收敛曲线(几何非线性)Fig. 5 Convergence studies of the half-circle arc beam(geometrically nonlinear)

对于非线性动力学分析，分别采用2、3、4 次NURBS 单元，单元数量为34，其中部受集中力载荷F= 3115 N，加载时间历程为0.07 s，时间步长为 7×10-4s，共100 时间步。在线下(offline)计算过程中，首先对曲梁结构进行动力学分析，搜集每个时间步所对应的位移向量与刚度矩阵向量，再对位移以及刚度矩阵向量快照集合Usnap和KTsnap采用奇异值分解，得到基底向量ZU、ZK以及对应的奇异值 ΣU、 ΣK。图6 所示为不同阶次NURBS 单元的位移以及刚度矩阵向量所对应的奇异值分布图，可以看出阶次变化对奇异值影响不大。

图6 两端固支半圆弧曲梁奇异值Fig. 6 Singular values of displacement snapshots and stiffness matrix snapshots for polynomial degrees 2, 3, 4 for clamped half-circle arc

选取k= 20 阶位移基底向量作为模型降阶基底，选取m= 15 阶刚度矩阵基底向量作为MDEIM基底，根据误差估计式(39)计算可得逼近误差为10-6%量级，具有足够的精度。线上(online)计算采用与线下计算相同的载荷步长、加载时间历程及载荷大小，计算结果如图7所示。由图可见，当NURBS 单元为2 阶时，全阶模型与降阶模型的位移载荷曲线与ABAQUS 参考值有一定偏差，这主要是由于2 阶NURBS 单元存在一定的薄膜闭锁现象，使其刚度偏大，从而导致了偏差，当NURBS 单元阶数升高为3 阶、4 阶时，其位移载荷曲线与ABAQUS 参考值吻合良好，体现了升阶对于消除等几何曲梁单元闭锁的效果，避免了构造无闭锁单元的麻烦。因此本算例采用3 阶NURBS 基函数进行后续计算。

图7 两端固支半圆弧曲梁载荷-位移曲线Fig. 7 Load-displacement response of half-circle arc beam

图8、图9 所示为采用全阶以及降阶模型所获得的曲梁中点的运动轨迹对比图以及两者差值的分布图。由于所选模型是左、右对称的，因此其x方向位移较小，可忽略不计，观察y方向位移可以发现，降阶模型与原阶模型位移范围基本一致(如图8 所示)，误差范围在-1.25 mm～0.75 mm(如图9 所示)，无量纲化后约为10-4量级，表明降阶模型具有较高的精度。

图8 两端固支半圆弧曲梁中点轨迹对比图Fig. 8 Comparison of the paths traced by the mid-point of the half-circle arc beam obtained using the FOM and ROM

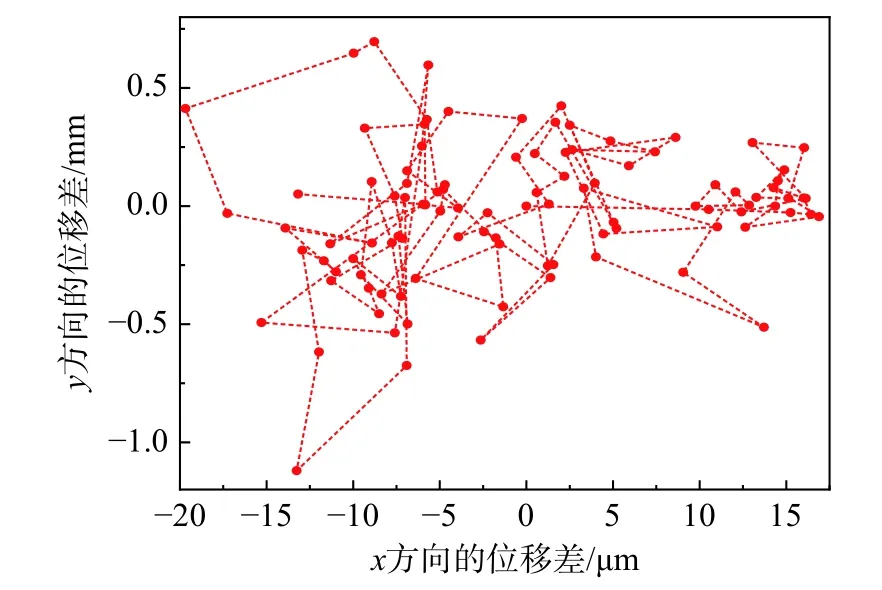
图9 两端固支半圆弧曲梁降阶与全阶模型位移差值图Fig. 9 Difference of mid-point displacement between FOM and ROM for half-circle arc beam

降阶模型的计算时间对比见表1。由表可见，当只采用POD 模型降阶方法时，其计算时间相比全阶模型提升有限；当只选取前2 阶基底作为模型降阶基底时，其计算时间加速率(时间比)仅为1.4，效率提升较为有限。这主要是由于POD 降阶模型需要重复计算曲梁的刚度矩阵所导致。当采用POD-MDEIM 降阶模型时，其计算时间加速率为8.2，显然，MDEIM 方法显著降低了刚度矩阵的计算时间，从而大大提升了降阶模型的求解效率。

表1 两端固支半圆弧曲梁降阶模型计算时间对比Table 1 Comparisons of computational time for reduced order models of half-circle arc beam

表2 所示为采用POD-MDEIM 方法所得到的刚度矩阵列向量的插值位置以及包含该位置的单元编号。由表可见，对于两端固支半圆弧曲梁模型，只需计算15 个位置处的刚度矩阵值即可通过插值矩阵D对刚度矩阵列向量进行重构，但由于每个NURBS 基函数的支撑区域包含p+1 个节点区间，因此所涉及的单元编号数量相比插值位置的个数更多。

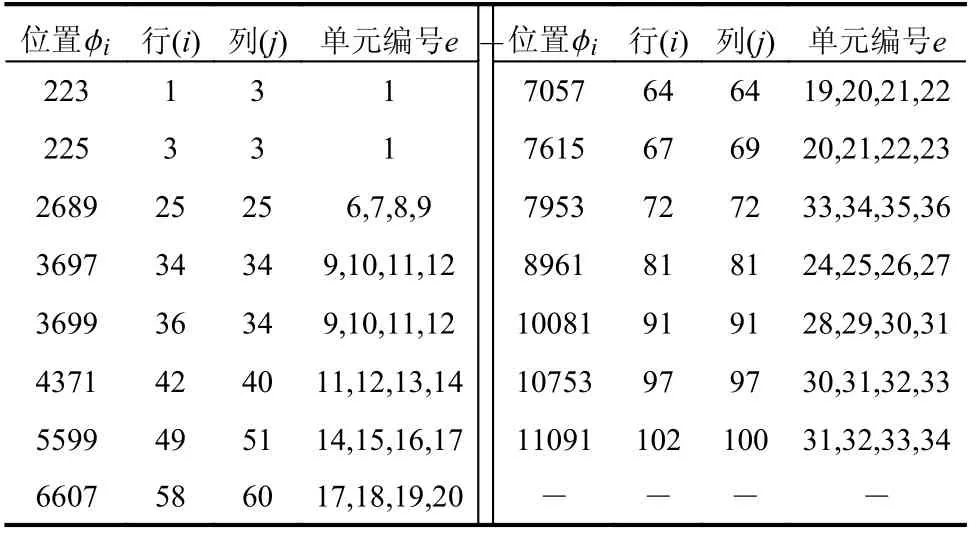
表2 两端简支曲梁刚度矩阵MDEIM 插值位置Table 2 MDEIM Positions for stiffness matrix of simply supported arc beam

图10 所示为不同单元数量对降阶模型计算效率的影响。可见，降阶模型与全阶模型的计算时间随着单元数量的增大呈线性增长趋势，体现了该降阶模型对于不同模型的适应性。

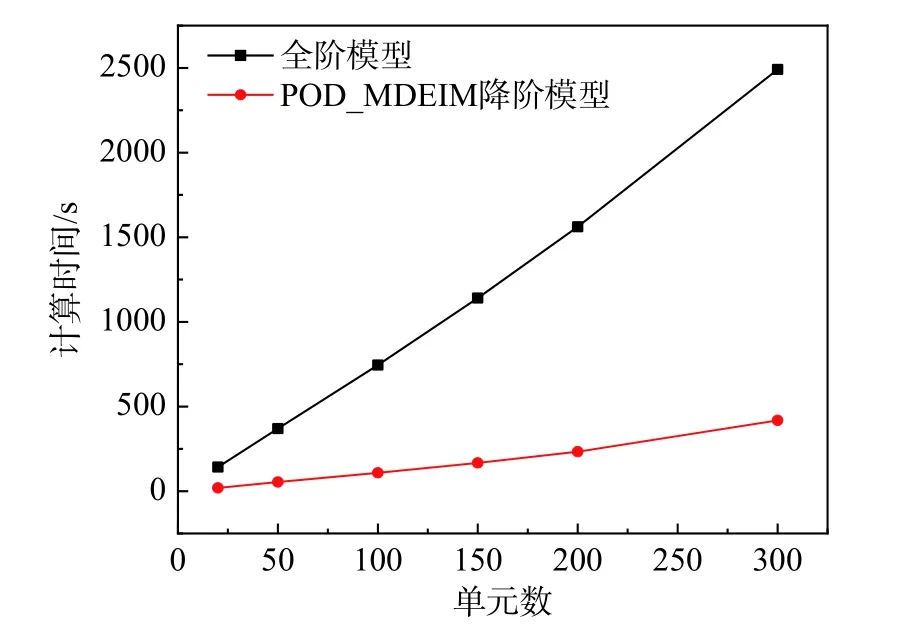
图10 两端固支半圆弧曲梁降阶、全阶模型计算时间对比Fig. 10 Comparison of computational time for different reduced order models of half-circle arc beam

4.2 一端固支阿基米德螺旋曲梁

如图11 所示为一端固支的阿基米德螺旋曲梁模型，几何描述为r=5+2θ/m,θ ∈[0,2π]，另一端点 ξ=1 处受集中力F=80 N 载荷，横截面宽度和高度分别为b=h=0.5 m，弹性模量E=1.2×106Pa，密度 ρ0=1 kg/m-3，曲梁模型采用3 次NURBS单元描述，单元数为40。

图11 一端固支阿基米德螺旋梁Fig. 11 Archimedes spiral shaped beam with one end clamped

线下计算时，载荷时间历程为10 s，共300 个时间步。对位移及刚度矩阵快照集合Usnap和KTsnap进行奇异值分解，得到奇异值分布(图12)。

图12 一端固支阿基米德螺旋曲梁奇异值Fig. 12 Singular values of displacement snapshots and stiffness matrix snapshots for clamped Archimedes spiral beam

选取k= 23 阶位移基底向量作为模型降阶基底，选取前m= 30 阶刚度矩阵基底向量作为MDEIM 基底。根据误差估计公式(39)可知，所选取的位移以及刚度矩阵基底的逼近误差分别为1.85×10-6% 和6.81×10-5%，因此具有足够的精度。

线上(online)计算过程中采用与线下计算相同的载荷步长、加载时间历程及载荷大小，计算结果如图13 所示。降阶模型与全阶模型吻合良好，表明降阶模型具有较高的精度。在计算时间上，全阶模型计算时间为460.25 s，而POD-MDEIM降阶模型计算时间为64 s，速度提升率为13.8。

图13 一端固支阿基米德螺旋曲梁载荷位移曲线Fig. 13 Load-displacement curve of clamped Archimedes spiral arc beam

图14 所示为阿基米德螺旋曲梁端点轨迹对比图，图15 所示为全阶模型与降阶模型曲梁在端点处的位移差值。由图可见，降阶模型与全阶模型的位移误差较小，x方向位移误差约为10-5m，y方向位移误差约为10-6m 的水平，体现了降阶模型的计算精度。

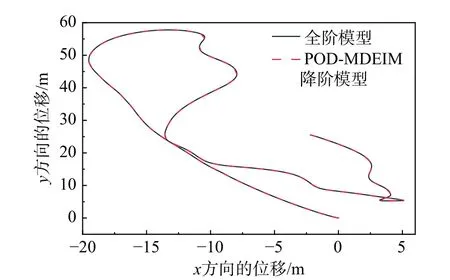
图14 一端固支阿基米德螺旋曲梁端点的轨迹对比图Fig. 14 Comparison of the paths traced by the end-point of the Archimedes spiral beam obtained using the FOM and ROM

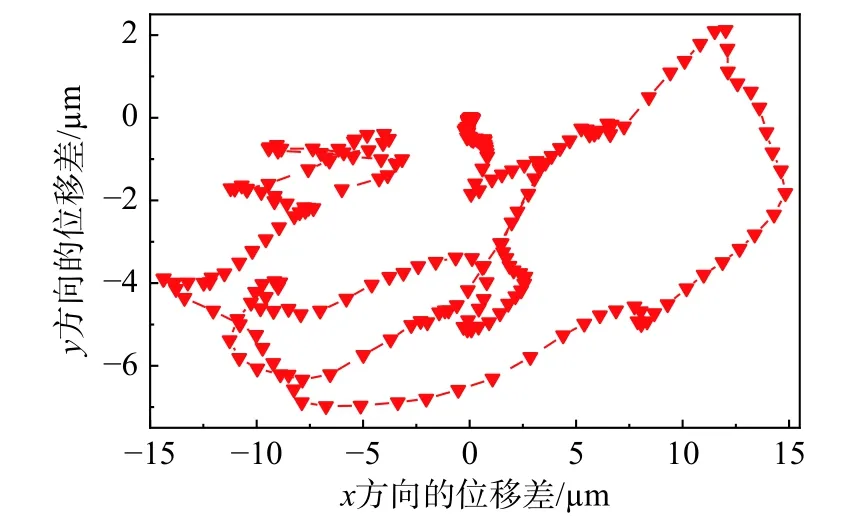
图15 阿基米德螺旋曲梁端点降阶与全阶模型位移差值图Fig. 15 Difference of end-point displacement between FOM and ROM for the Archimedes spiral beam

4.3 两端简支曲梁

如图16 所示为一两端简支曲梁模型，中点处ξ=0.5 受集中力F=800 N载荷，其跨度L= 10 m，横截面宽度和高度分别为b=h= 0.5 m，曲梁采用二次NURBS 曲线描述，单元数为1，因此具有3 个控制点，其中间控制点坐标为P2=(5,4)m。曲梁弹性模量E=1.2×106Pa ，密度 ρ0=1 kg/m3，为了获得较高计算精度，将曲梁细化为37 个单元，阶数提升为3 阶，基于等几何分析的特点，对曲梁进行细化不会改变其几何形状。

图16 两端简支曲梁模型Fig. 16 Arc beam with simply supported boundary conditions at both ends

线下计算时，载荷时间历程为1 s，时间步长设为0.01 s，共100 个时间步。对位移以及刚度矩阵快照集合Usnap和KTsnap进行奇异值分解，得到奇异值分布(如图17 所示)。

图17 两端简支曲梁奇异值Fig. 17 Singular values of displacement snapshots and stiffness matrix snapshots for simply supported arc beam

选取k= 20 阶位移基底向量作为模型降阶基底，选取前m= 15 阶刚度矩阵基底向量作为MDEIM 基底。根据误差估计公式(39)可知，选取的位移及刚度矩阵基底的逼近误差分别为1.91×10-8% 和1.34×10-7%，因此具有足够的精度。通过MDEIM 插值算法可以得到插值位置向量 φ，继而得到位置向量中每个元素在刚度矩阵中对应的行和列，从而可以得到包含这些特定位置元素的单元编号(见表3)。

观察表3 可知，采用MDEIM 算法，选取前15 阶插值基底，需要计算15 个位置处的刚度矩阵值，涉及的单元编号为：1, 8～25, 30～37，共27 个单元，但在每个单元中，无需计算所有的元素值，只需计算给定位置处的元素，因此，可以显著提升计算效率。

表3 两端简支曲梁刚度矩阵MDEIM 插值位置Table 3 MDEIM Positions for stiffness matrix of simply supported arc beam

线上(online)计算过程中采用与线下计算相同的载荷步长、加载时间历程及载荷大小，计算结果如图18 所示，降阶模型与全阶模型吻合良好，表明降阶模型具有较高的精度。在计算时间上，全阶模型计算时间为281.6 s，而POD-MDEIM 降阶模型计算时间为33.2 s，速度提升率为8.5。

图18 两端简支曲梁载荷-位移曲线Fig. 18 Load-displacement curve of simply supported arc beam

图19 所示为两端简支曲梁中点轨迹对比图，图20 所示为全阶模型与降阶模型曲梁在中点处的位移差值。由图可见，降阶模型与全阶模型的位移误差较小，y方向位移误差约为10-6m 的水平，体现了降阶模型的计算精度。

图19 两端简支曲梁中点的轨迹对比图Fig. 19 Comparison of the paths traced by the mid-point of the arc beam obtained using the FOM and ROM

图20 两端简支曲梁降阶与全阶模型位移差值图Fig. 20 Difference of mid-point displacement between FOM and ROM for the arc beam

图21 所示为两端简支曲梁全阶模型与降阶模型的频率响应对比图，频率响应可以通过曲梁模型中点位移的快速傅里叶变换得到。由图可见，在频率范围内，降阶模型与原阶模型亦吻合良好。

图21 两端简支曲梁频率响应对比图Fig. 21 Comparison of frequency response obtained using FOM and ROM

保持载荷时间历程及时间步长不变，将外载荷(单位：N)变为F=-800sin(36t)，通过在线模式进行非线性动力学计算，其载荷位移曲线如图22所示。由图可见，变换载荷后，降阶模型所得结果与原阶模型吻合良好，拓展了降阶模型的适用范围。在计算时间上，全阶模型所需计算时间为252.9 s，POD-MDEIM 降阶模型计算时间为33.5 s，速度提升率为7.5。

图22 两端简支曲梁载荷位移曲线( F=-800sin(36t))Fig. 22 Load-displacement curve of simply supported arc beam ( F=-800sin(36t))

图23、图24 分别为曲梁受外载荷F=-800sin(36t)时，其中点轨迹对比图以及位移差值图，可以观察到，降阶模型与全阶模型在y方向的位移误差约为10-5m 的水平。如图25 所示为改变外载荷后，曲梁全阶模型与降阶模型频率响应对比图，两者吻合良好。从图23～图25 中可以观察到，本文提出的降阶模型对于变载荷情况也能得到高精度的解。

图23 两端简支曲梁中点的轨迹对比图( F=-800sin(36t))Fig. 23 Comparison of the paths traced by the mid-point of the arc beam obtained using the FOM and ROM(F=-800sin(36t))

图24 两端简支曲梁降阶与全阶模型位移差值图(F=-800sin(36t))Fig. 24 Difference of mid-point displacement between FOM and ROM for the arc beam ( F=-800sin(36t))

图25 两端简支曲梁频率响应对比图( F=-800sin(36t))Fig. 25 Comparison of frequency response obtained using FOM and ROM ( F=-800sin(36t))

4.4 参数化两端简支曲梁

图26 所示为两端简支曲梁的参数化模型，曲梁模型参数与算例4.3 相同。其由二阶NURBS曲线描述，单元数为1，通过改变中间控制点P2的位置坐标可以实现曲梁几何模型的参数化。假设中间控制点P2可在x∈[2,8] m，y∈[0,10] m范围内取任意值，由于对称性，故只需考虑范围x∈[5,8] m，y∈[0,10] m (如图26 中虚线方框所示)。

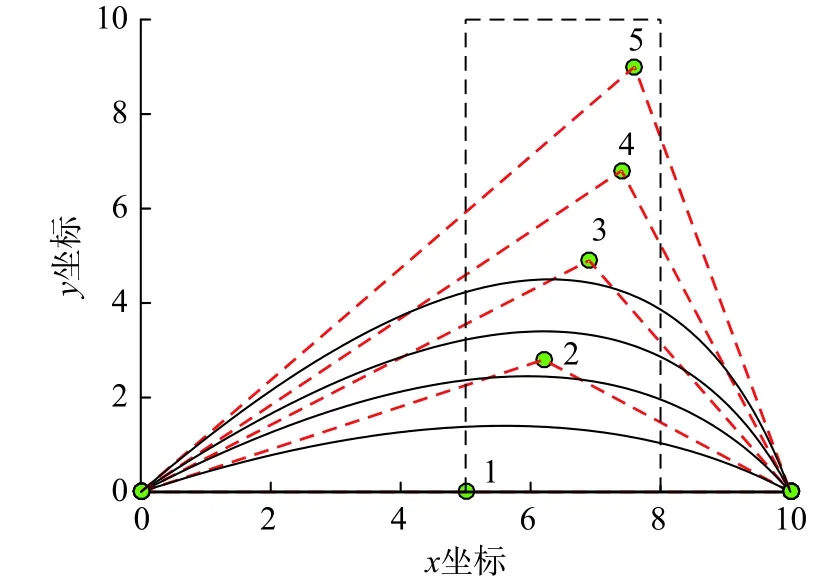
图26 两端简支曲梁的参数化模型Fig. 26 Parametric model of simply supported curved beams

曲梁模型中点处 (ξ=0.5) 受集中力载荷F=-800 N，为了获得较高计算精度，将曲梁细化为31 个单元，阶数提升为3 阶。由于等几何分析模型与几何模型保持一致，故无需进行额外的模型转换等工作，并且，模型的细化并不会改变其几何形状，这对模型的参数化提供了便利。

为了准确捕捉不同参数下结构的位移载荷响应特征，本算例采用了两种不同抽样方法，即相对均匀抽样(抽样方法1)以及拉丁超立方抽样(抽样方法2)，在范围x∈[5,8] m，y∈[0,10] m 中生成控制点P2的坐标样本，如图27 中绿色控制点所示，其中，相对均匀抽样点数为101 个，拉丁超立方抽样点数为100。

图27 控制点P2 抽样分布图Fig. 27 Sampling positions of the control point P2

线下计算时，分别对每个抽样控制点所对应的曲梁模型进行非线性动力学分析，并搜集位移以及刚度矩阵快照集合Usnap和KTsnap。对两种抽样方法所获得的快照集合分别进行奇异值分解，得到奇异值如图28 所示。

图28 参数化曲梁奇异值Fig. 28 Singular values of displacement snapshots and stiffness matrix snapshots for parameterized arc beam

选取k= 20 阶位移基底向量作为模型降阶基底，选取前m= 50 阶刚度矩阵基底向量作为MDEIM基底。根据误差估计公式(39)可知，所选取的位移以及刚度矩阵基底的逼近误差分别为：1.23×10-5% 和9.78×10-6% (抽样法1)， 9.06×10-6%和7.37×10-6%(抽样法2)，因此具有足够的精度。

在线上计算模式中，为了验证POD-MDEIM模型降阶方法的精度及可靠性，在范围x∈[5,8] m，y∈[0,10]m 中任意选择与抽样点不相重合的控制点，建立曲梁模型，进行非线性动力学降阶模型计算。选取控制点P2坐标为(7.5,9.5) m，(5.7,7.2) m。基于上述两种抽样方法所构建的降阶模型，进行非线性动力学分析，其位移载荷响应如图29 所示，可以观察到，对于不同抽样方法，POD-MDEIM降阶模型所得结果与原阶模型吻合良好，验证了所提出的降阶模型的可靠性以及准确性。

图29 不同抽样方法所对应的位移载荷响应Fig. 29 Load-displacement response of half-circle arc beam

图30、图31 所示分别为P2=(7.5,9.5) m 及P2= (5.7,7.2) m 时，降阶模型与全阶模型在ξ=0.5处的轨迹对比图以及位移差值图。由于参数化曲梁不再是对称模型，因此需要考虑其x方向位移，可以观察到，对于不同抽样方法，降阶模型与全阶模型在 ξ=0.5处的运动轨迹均吻合良好，且位移误差约为10-3m 的水平。

图30 参数化曲梁 ξ=0.5处的轨迹对比图Fig. 30 Comparison of the paths traced at the position of ξ=0.5for the parameterized arc beam obtained using the FOM and ROM

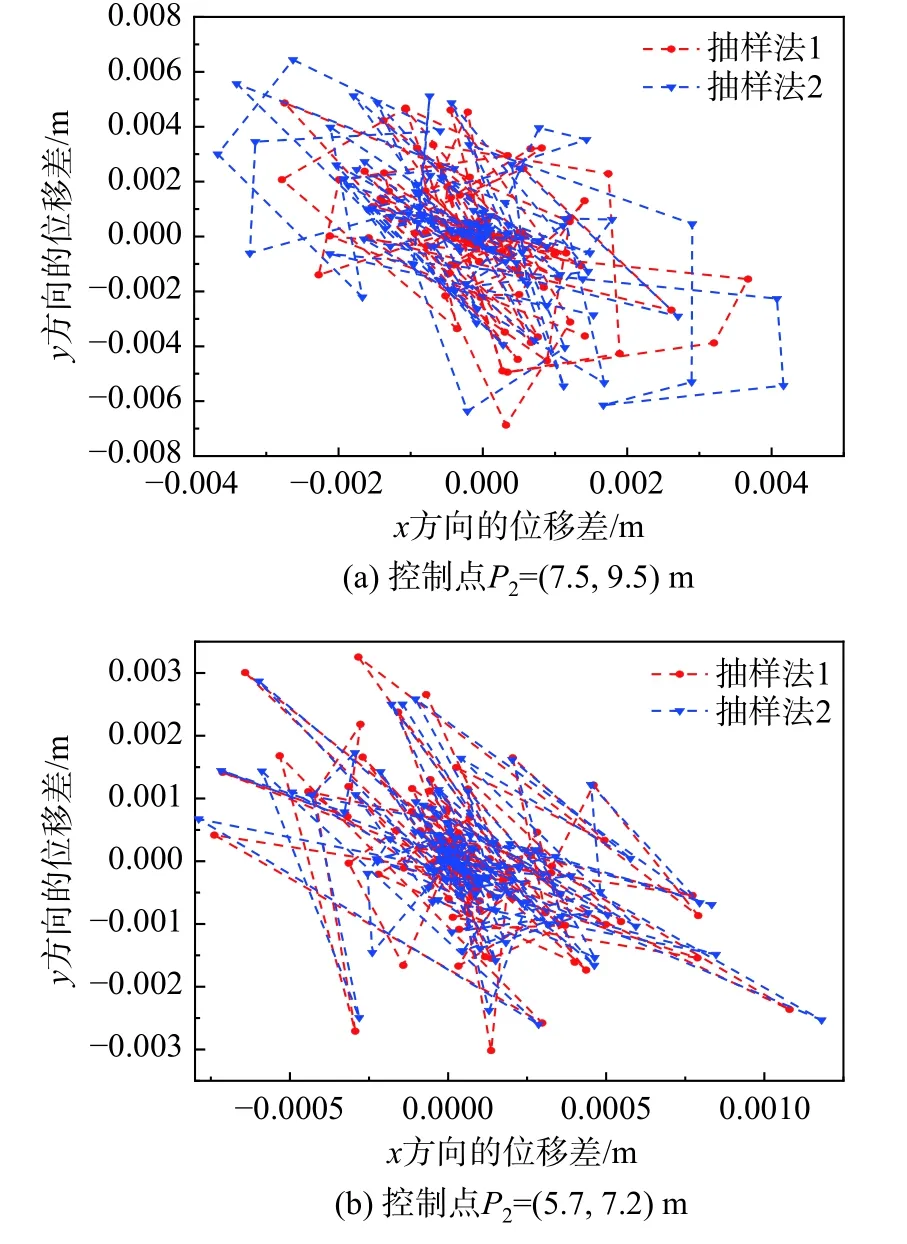
图31 参数化曲梁降阶与全阶模型位移差值图(ξ=0.5)Fig. 31 Difference of the displacement between FOM and ROM for the parameterized arc beam (ξ=0.5)

图32 所示为参数化曲梁降阶模型与全阶模型的频率响应对比图。可以观察到，对于不同取样方法以及不同控制点位置，降阶模型与全阶模型在频域内吻合良好。

图32 参数化曲梁频率响应对比图Fig. 32 Comparison of frequency response obtained using FOM and ROM for the parameterized arc beam

为了研究本文所提出的降阶模型对于变载荷以及变时间步长的适应性，以下分2 种情况进行讨论：首先，保持载荷时间历程(1 s)和时间步长(0.01 s)不变，外力载荷(N)变为F=-800sin(48t)；其次，保持上述载荷时间历程和外载荷大小(N)不变(F=-800sin(48t))，减小时间步长为0.005 s，选择控制点P2坐标为(6, 5.5) m。针对上述两种情况分别对两种抽样方法所建立的降阶模型进行非线性动力学计算，所得载荷时间历程曲线如图33和图34 所示，从图中可以观察到，对于不同载荷以及时间步长，采用不同抽样方法所建立的降阶模型与原阶模型吻合良好，体现了降阶模型的稳定性。

图33 不同抽样方法所对应的位移载荷响应(ξ=0.5)(F=-800sin(48t))Fig. 33 Comparisons of load-displacement histories of the parameterized arc beam at (ξ=0.5) ( F=-800sin(48t))

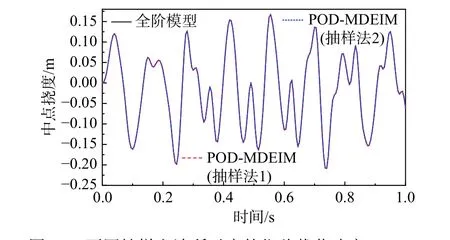
图34 不同抽样方法所对应的位移载荷响应(ξ=0.5)(F=-800sin(48t), 时间步长：0.005 s)Fig. 34 Comparisons of load-displacement histories of the parameterized arc beam at(ξ=0.5)(F=-800sin(48t), time step: 0.005 s)

图35 及图36 所示为变载荷、变时间步长情况下参数化曲梁在 (ξ=0.5)处轨迹对比图以及位移差值图。由图可见，对于两种不同抽样方法，降阶模型与全阶模型均吻合良好，位移误差约为10-3m的水平。图37 所示为降阶模型与全阶模型频率响应对比图，两者吻合良好。图35～图37 体现了参数化降阶模型对于不同载荷以及不同抽样方法的适应性。

图35 参数化曲梁 (ξ=0.5)处的轨迹对比图(F=-800sin(48t), 时间步长：0.005 s)Fig. 35 Comparison of the paths traced at the position of(ξ=0.5)for the parameterized arc beam obtained using the FOM and ROM ( F=-800sin(48t), time step: 0.005 s)

图36 参数化曲梁降阶与全阶模型位移差值图(ξ=0.5) (F=-800sin(48t), 时间步长：0.005 s)Fig. 36 Difference of the displacement between FOM and ROM for the parameterized arc beam(ξ=0.5)(F=-800sin(48t), time step: 0.005 s)

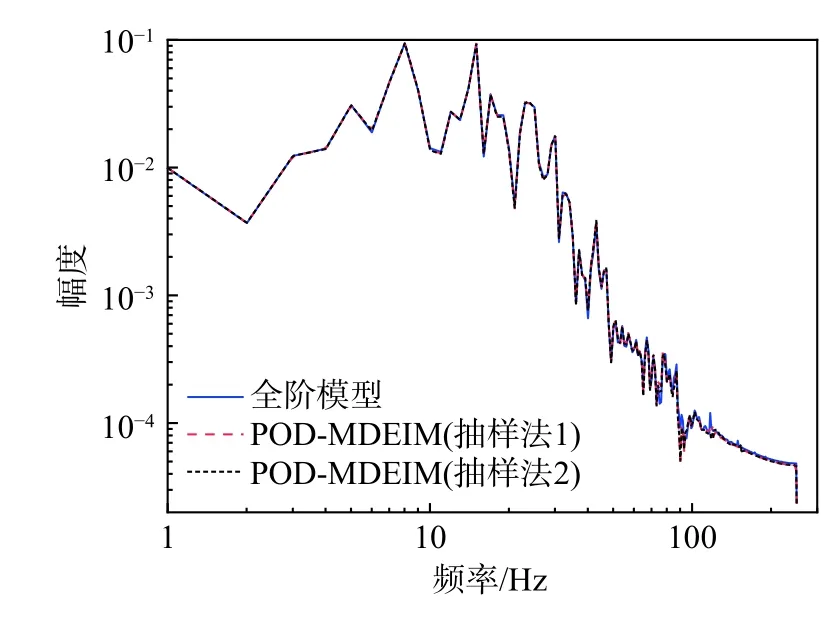
图37 参数化曲梁频率响应对比图(F=-800sin(48t), 时间步长：0.005 s)Fig. 37 Comparison of frequency response obtained using FOM and ROM for the parameterized arc beam(F=-800sin(48t), time step: 0.005 s)

降阶模型的计算时间对比如表4 所示。由表可见，POD-MDEIM 降阶模型对于计算效率的提升较为显著，且对于不同抽样方法、不同计算样本，以及不同的外载荷，均体现出了较高的速度提升效果，体现了降阶模型的稳定性及适应性。